Ant colony optimization based founder sequence reconstruction

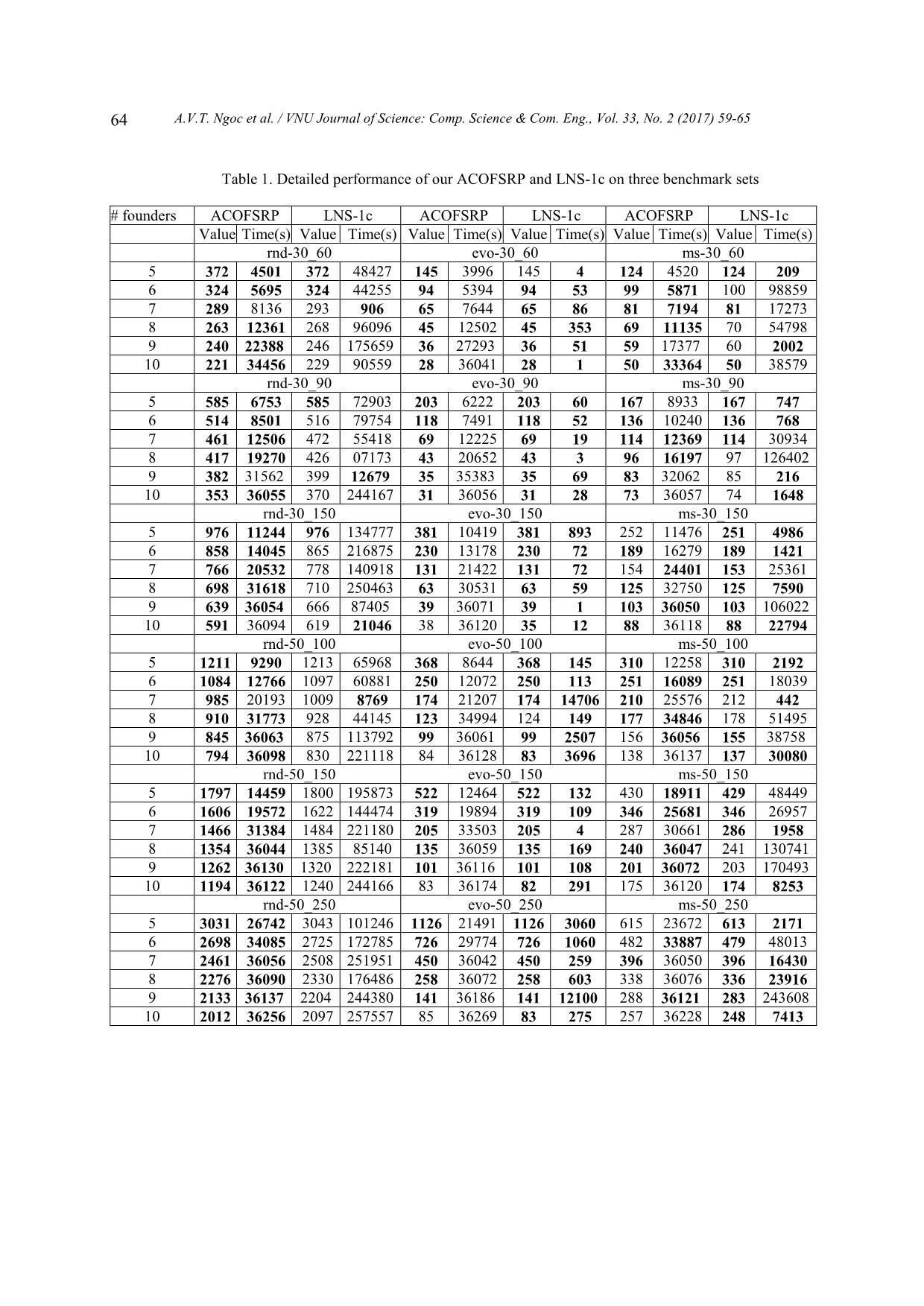
e may ignore 
1l
V 
for downstream analysis. 
3.2. Large neighborhood search algorithm 
LNS-1c is empirically considered the best 
algorithm proposed by far for solving the FSR 
problem [4]. This algorithm uses the nearest-
neighbor search strategy over a large 
neighborhood of constructed solutions. 
During searching the neighborhood, the 
algorithm picks out a set FFfree beforehand, 
then uses the algorithm Recblock to search for 
alternative founder sequences in freeFF . 
Whenever a better solution is found out, LNS-
1c performs local search over neighborhood 
from scratch. 
4 Proposed method 
4.1. Ant colony optimization based FSR 
Ant colony optimization [7] (ACO) is a 
metaheuristic method simulating how ants in 
nature find paths from their nest to food 
sources, which turn out to be a reinforcement 
learning method. ACO solves optimization 
problems throughout many episodes, in each of 
which every ant travels to find solutions based 
on heuristic information and pheromone matrix 
 containing information learned. The best 
solution found in the current episode is used to 
learn (tune  ) and go for the next turn. 
Our proposed method for FSR has input and 
output as follows: 
Input: binary matrix C of size mn* 
representing a recombinant set and k is the 
number of the founder sequences to be found. 
Output: binary matrix F of size mk * 
string representing the founder sequences so 
that ),( FCBP is minimal. Here, ),( FCBP is 
the number of breakpoints required to obtain C 
from F . 
In general, our ACO based method for FSR 
works as depicted in Algorithm 1: 
4.2. Structure graph for the FSR problem 
For the sake of visualization, we simulate 
the FSR problem as the problem of finding 
paths on a corresponding structure graph (see 
Figure 2). 
This structure graph includes a start, an end 
node and m columns. Each column has k2 
vertices, of which each corresponds to a state of 
the corresponding column in the matrix F of 
founder sequences. In particularly, each state is 
a binary string of length k . 
Each vertex has edges connecting to all 
ones in the next column. We can see all paths 
starting from the start to the end node has to go 
through every column once, at which one state 
is chosen. Each journey of ants travelling from 
the start to the end node therefore corresponds 
to a complete matrix of founder sequences. 
4.3. How ants travel on the structure graph 
When travelling on the structure graph, ants 
chose a next vertex to visit at random. The 
A.V.T. Ngoc et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 33, No. 2 (2017) 59-65 
62
algorithm is described in pseudo code in 
Algorithm ??. The probability at which a vertex 
is chosen is proportional to its level of 
compatibility to the matrix constructed by ants 
so far. This level is calculated through heuristic 
and pheromone information  . Particularly, 
the j vertex in the column i will be visited by 
an ant with a probability. 
 
 


][][
][][
=
,,
,,
,
lali
l
jaji
jiP

Where: 
• ja, is the heuristic value (see 4.3.1). 
• ji , is the pheromone information (see 
4.3.2). 
•  , are two parameters of an ACO 
determining the correlation between the 
heuristic value and the pheromone information. 
4.3.1. Heuristic information 
While constructing the optimal solution, 
heuristic information is calculated according to 
the level of compatibility to the matrix that is 
yielded with the next moves of ants. In more 
details, when an ant is going to the j vertex in 
the column i the heuristic information is 
calculated as follows. 
),(
1
=,
jFCBP ai
ja

where: 
• iC is the matrix of the first i columns of 
matrix C . 
• aF is the solution that ant a has built 
(with 1 i columns). 
• jFa is the matrix resulted when ant a 
intends to visit vertex j . 
To give an example, when 3=i we have 
the structure graph as in Figure 3. 
Figure 3. Structure graph when i = 3. 
4.3.2. Pheromone information 
In the FSR problem, we denote ij as the 
pheromone information of the thj vertex in the 
column i in the graph. Vertices being visited in 
the optimal solutions found in every searching 
phase by ants so far will be learnt such that they 
are of high priority to be visited in next phases. 
There are various pheromone updating 
methods that have been proposed for ACO. We 
select the Smoothed Max-Min Ant system [8] 
because it yields the best results in our 
experiments. In this regard, the pheromone 
information is updated after each loop as follows: 
ijijij   )(1= 
where: 
Tjiif
Tjiif
max
min
ij ),(
),(
=
 
 
and T is the optimal solution that ants found 
after the loop and ),( ji is the vertex j in the 
column i of the structure graph. 
4.4. Improved ACO for FSRP 
4.4.1 Ants find solutions synchronously 
Note that the problem solution space is 
extremely large, if working independently with 
Figure 2. Structure graph for the ACO-based 
founder sequence reconstruction. 
A.V.T. Ngoc et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 33, No. 2 (2017) 59-65 63
each other ants could hardly to concentrate on 
potential regions of the searching space. We 
therefore propose a search strategy for ants as 
follows: 
We let ants (in the set Ants) find solutions 
in parallel. When moving to the next column, 
instead of letting each ant choose the next 
vertex to go, we create a new ant set (called 
NewAnts) to prolong paths created by ants in 
the set Ants. In particular, if an ant a prolongs 
the path for an ant a , it means that ant a will 
go over the similar journey as ant a before 
moving to the next vertex in the next column. 
When having NewAnts with the same size as 
Ants, we move to the next column and repeat 
such a new ant set building procedure from 
NewAnts until having a complete solution set. 
This procedure is depicted in pseudo code in 
Algorithm 3. 
For more details, when going from the 
column 1 i to the column i , each ant 
NewAntsa will randomly choose an ant 
Antsa to prolong its path and a vertex j in 
the column i to move forward. The ant a is 
chosen with a probability also based on the 
heuristic and pheromone information, as 
follows: 
 
 


][][
][][
=
,,
,,
,
lxali
lxa
jaji
jaP

4.4.2. Other improvements 
Neighborhood search: To lower the 
probability of missing good solutions while 
searching, we recommend using the reduced 
version of the algorithm RecBlock (3.2) to find 
other better solutions within the vicinity of the best 
by far solution found by ants. Instead of browsing 
the whole founder sequences, for each founder in 
the optimal solution found by far we use RecBlock 
to find another alternative better one. 
Searching along two dimensions: With the 
newly proposed search strategy, ants will 
quickly converge onto some solution regions, 
leading to a low diversity of found solutions. To 
improve this problem, apart from searching 
forward from the start to the end vertex, we also 
let ants search backward along the opposite 
direction (i.e. from the end back to start vertex). 
The search direction is periodically changed. 
When searching backward, the complete 
different heuristic information is used, leading 
to the potential of finding new solutions. 
5. Experimental results 
We compare our proposed FSR algorithm 
called ACOFSRP with the best corresponding 
one by far, i.e. LNS-1c [4] on 3 benchmark data 
sets, namely rnd (random), evo and ms (each 
contains 6 test set). All sequences in the first 
data set is randomly generated while those in 
the two latter ones are generated according to 
evolutionary models. All three are used in the 
study of LNS-1c. We do experiments with the 
founder sequence length 105,6,7,8,9, k for 
each of such 3 test sets, leading to a total of 
108 tests. 
We also do experiments with different 
variants of ACOFSRP by not using either one 
of two improvements or both on the same three 
benchmark sets. Experimental results show that 
ACOFSRP outperforms its two variants, 
demonstrating the power of two proposed 
improvements in ACOFSRP (data not shown). 
Due to the random nature of ACOFSRP, we 
perform each test 20 times and the run time of 
each is limited to 10 hours. These numbers are 
1 and 72, respectively, in the study of LNS-1c 
[4]. The program is run on a CPU with 12GB 
RAM and 4GHz processor. Table ?? shows the 
detailed performance, in terms of the solution 
quality (number of required breakpoints) and 
the running time, of ACOFSRP and LNS-1c on 
three benchmark data sets. Note that the values 
for ACOFSRP are the averages of those from 
20 running times. 
A.V.T. Ngoc et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 33, No. 2 (2017) 59-65 
64
Table 1. Detailed performance of our ACOFSRP and LNS-1c on three benchmark sets 
# founders ACOFSRP LNS-1c ACOFSRP LNS-1c ACOFSRP LNS-1c 
 Value Time(s) Value Time(s) Value Time(s) Value Time(s) Value Time(s) Value Time(s) 
 rnd-30_60 evo-30_60 ms-30_60 
5 372 4501 372 48427 145 3996 145 4 124 4520 124 209 
6 324 5695 324 44255 94 5394 94 53 99 5871 100 98859 
7 289 8136 293 906 65 7644 65 86 81 7194 81 17273 
8 263 12361 268 96096 45 12502 45 353 69 11135 70 54798 
9 240 22388 246 175659 36 27293 36 51 59 17377 60 2002 
10 221 34456 229 90559 28 36041 28 1 50 33364 50 38579 
 rnd-30_90 evo-30_90 ms-30_90 
5 585 6753 585 72903 203 6222 203 60 167 8933 167 747 
6 514 8501 516 79754 118 7491 118 52 136 10240 136 768 
7 461 12506 472 55418 69 12225 69 19 114 12369 114 30934 
8 417 19270 426 07173 43 20652 43 3 96 16197 97 126402 
9 382 31562 399 12679 35 35383 35 69 83 32062 85 216 
10 353 36055 370 244167 31 36056 31 28 73 36057 74 1648 
 rnd-30_150 evo-30_150 ms-30_150 
5 976 11244 976 134777 381 10419 381 893 252 11476 251 4986 
6 858 14045 865 216875 230 13178 230 72 189 16279 189 1421 
7 766 20532 778 140918 131 21422 131 72 154 24401 153 25361 
8 698 31618 710 250463 63 30531 63 59 125 32750 125 7590 
9 639 36054 666 87405 39 36071 39 1 103 36050 103 106022 
10 591 36094 619 21046 38 36120 35 12 88 36118 88 22794 
 rnd-50_100 evo-50_100 ms-50_100 
5 1211 9290 1213 65968 368 8644 368 145 310 12258 310 2192 
6 1084 12766 1097 60881 250 12072 250 113 251 16089 251 18039 
7 985 20193 1009 8769 174 21207 174 14706 210 25576 212 442 
8 910 31773 928 44145 123 34994 124 149 177 34846 178 51495 
9 845 36063 875 113792 99 36061 99 2507 156 36056 155 38758 
10 794 36098 830 221118 84 36128 83 3696 138 36137 137 30080 
 rnd-50_150 evo-50_150 ms-50_150 
5 1797 14459 1800 195873 522 12464 522 132 430 18911 429 48449 
6 1606 19572 1622 144474 319 19894 319 109 346 25681 346 26957 
7 1466 31384 1484 221180 205 33503 205 4 287 30661 286 1958 
8 1354 36044 1385 85140 135 36059 135 169 240 36047 241 130741 
9 1262 36130 1320 222181 101 36116 101 108 201 36072 203 170493 
10 1194 36122 1240 244166 83 36174 82 291 175 36120 174 8253 
 rnd-50_250 evo-50_250 ms-50_250 
5 3031 26742 3043 101246 1126 21491 1126 3060 615 23672 613 2171 
6 2698 34085 2725 172785 726 29774 726 1060 482 33887 479 48013 
7 2461 36056 2508 251951 450 36042 450 259 396 36050 396 16430 
8 2276 36090 2330 176486 258 36072 258 603 338 36076 336 23916 
9 2133 36137 2204 244380 141 36186 141 12100 288 36121 283 243608 
10 2012 36256 2097 257557 85 36269 83 275 257 36228 248 7413 
A.V.T. Ngoc et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 33, No. 2 (2017) 59-65 65
On the random data set ( rnd ), ACOFSRP 
could procedure solutions better than LNS-1c 
for 32 among total 36 cases. On-par solutions 
are observed in the 4 remaining cases. 
Regarding the running time, ACOFSRP 
requires shorter time than LNS-1c for 32 cases 
while longer only for 4 remaining cases. 
On the data set evo , ACOFSRP is beated 
by LNS-1c in terms of excution time for all 
cases. Nevertheless, solutions yielded by 
ACOFSRP are on-par with those of LNS-1c for 
32 out of 36 cases. For the remaining 4 cases, 
the solution goodness scores by ACOFSRP are 
worse than those by LNS-1c (The small 
differences are observed, i.e. up to 3 
breakpoints). 
On the data set ms , ACOFSRP produced 
solutions are better than and equal to those 
yielded by LNS-1c for 12 and 10 cases, 
respectively. Interestingly, among such 22, 
ACOFSRP requires remarkably shorter runing 
time than LNS-1c for 12 cases. For the 
remaining 14 cases, ACOFSRP produce 
solutions worse than LNS-
1c. ./table_combine_all.tex 
6. Conclusion 
Founder gene sequence reconstruction 
(FSR) for a given population can be modeled as 
a combinatorial optimization problem, which 
has been proven NP-hard. In this paper we 
propose a novel method based on ant colony 
optimization algorithms (ACO) coupled with 
two other important improvements (i.e. local 
search and back forward search) to solve the 
founder gene sequence reconstruction problem. 
Experiments on the benchmark data sets show 
better or equal results for almost sets when 
comparing to the best corresponding method, 
demonstrating the efficacy and future 
perspectives of our proposed method. 
Acknowledgments 
This work has been supported by Vietnam 
National University, Hanoi (VNU), under 
Project No. QG.15.21. 
References 
[1] G. Tyson, J. Chapman, H. Philip, E. Allen, R. 
Ram, P. M. Richardson, V. Solovyev, E. M. 
Rubin, D. Rokhsar, J. F. Banfield, Community 
structure and metabolism through 
reconstruction of microbial genomes from the 
environment, Nature 428 (2004) 37–43. 
[2] E. Ukkonen, Finding Founder Sequences from 
a Set of Recombinants, Springer Berlin 
Heidelberg, Berlin, Heidelberg, 2002, 
pp. 277–286. 
[3] A. Roli, C. Blum, Tabu Search for the Founder 
Sequence Reconstruction Problem: A 
Preliminary Study, Springer Berlin Heidelberg, 
Berlin, Heidelberg, 2009, pp. 1035–1042. 
[4] A. Roli, S. Benedettini, T. Stützle, C. Blum, 
Large neighbourhood search algorithms for the 
founder sequence reconstruction problem, 
Computers Operations Research 39 (2) (2012) 
pp. 213–224. 
[5] C. Blum, A. Roli, Metaheuristics in 
combinatorial optimization: Overview and 
conceptual comparison, ACM Comput. Surv. 
35 (3) (2003) 268–308. 
[6] P. Rastas, E. Ukkonen, Haplotype inference via 
hierarchical genotype parsing, in: Proceedings 
of the 7th International Conference on 
Algorithms in Bioinformatics, WABI’07, 
Springer-Verlag, Berlin, Heidelberg, 2007, 
pp. 85–97. 
[7] M. Dorigo, T. Stützle, Ant Colony 
Optimization, Bradford Company, Scituate, 
MA, USA, 2004. 
[8] D. Do Duc, H. Hoang Xuan, Smooth and three-
levels ant systems: Novel aco algorithms for 
solving traveling salesman problem, in: Ad. 
Cont. to the International Conference: IEEE-
RIVF 2010, pp. 33–37. 
G 
g