A study of fixed points and hopf bifurcation of hindmarshrose model

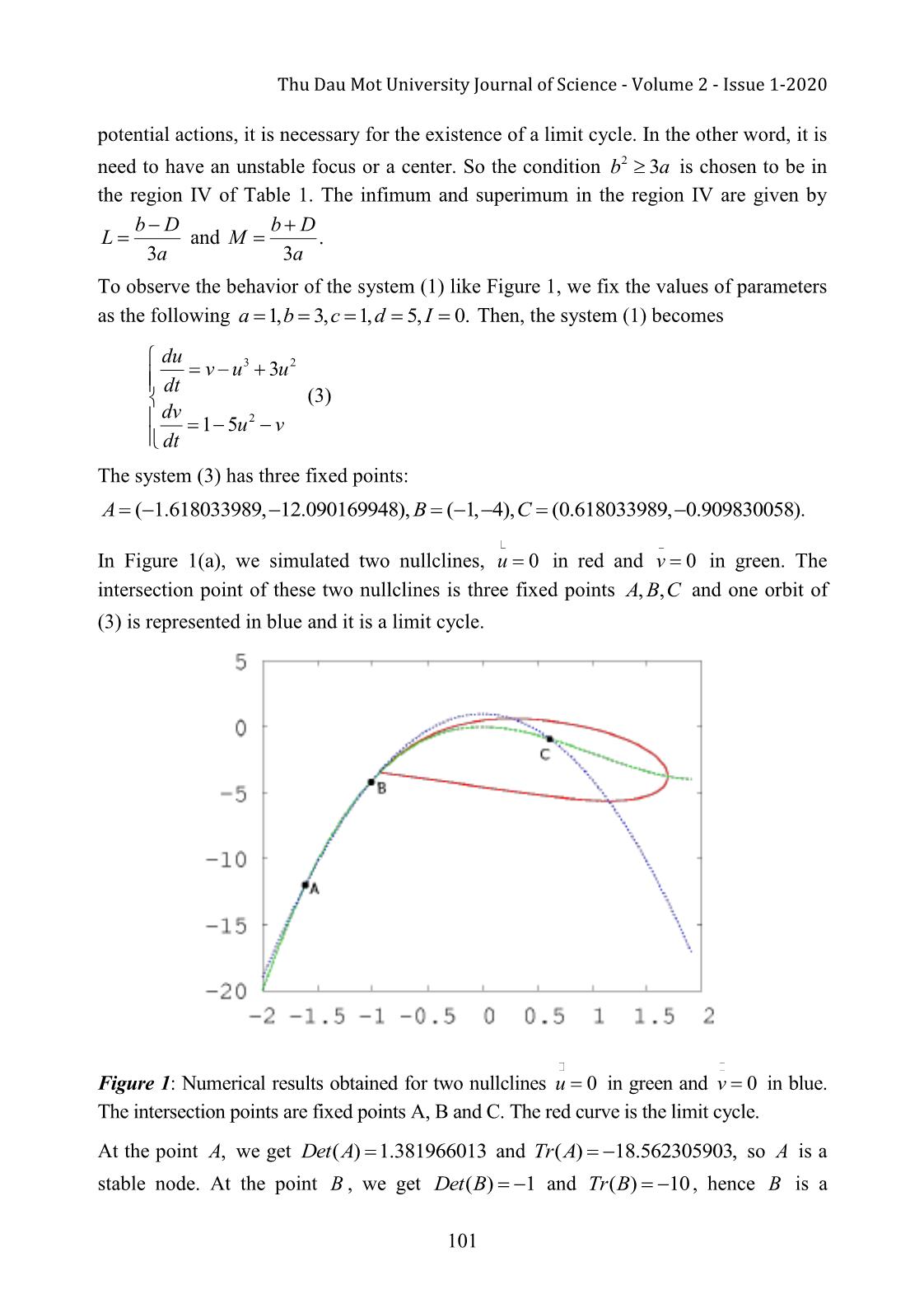
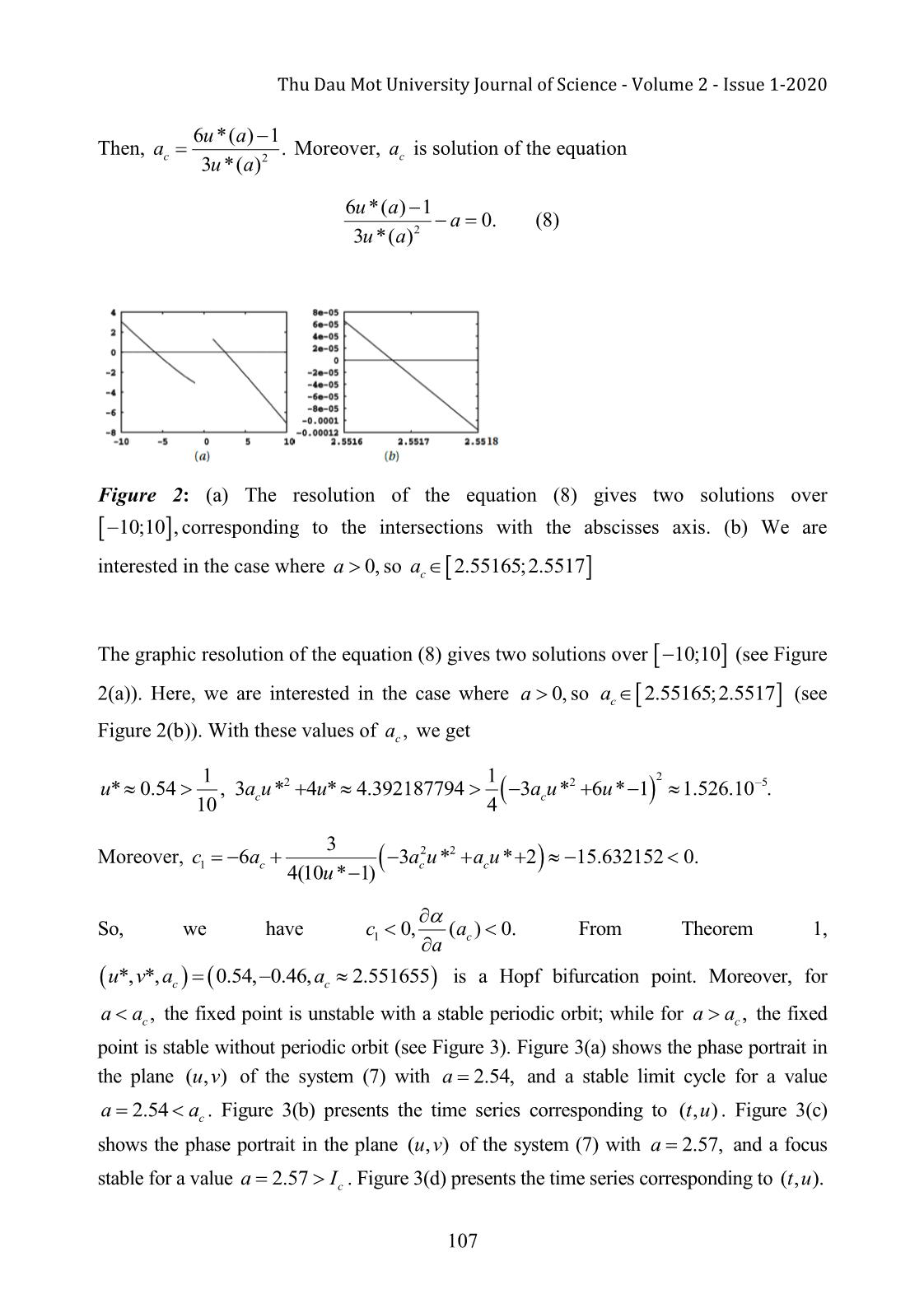
a pair of complex conjugate eigenvalues cross 
 the complex plane imaginary axis. Moreover, with the suitable assumptions for 
 the dynamical system, a small-amplitude limit cycle branches from the fixed point. 
 Keywords: Hindmarsh-Rose model, fixed point, Hopf bifurcation, limit cycle 
1. Introduction 
In the beginning of 1980s, Hindmarsh J.L. and Rose R.M. studied a model called 
Hindmarsh-Rose model, to expose part of the inner working mechanism of the Hodgkin-
Huxley equations, a famous model in study of neurophysiology since 1952. The 
Hindmarsh-Rose model was introduced as a dimensional reduction of the well-known 
Hodgkin-Huxley model (Hodgkin A. L., and Huxley A. F., 1952; Nagumo J., et al., 1962; 
 98 
 Thu Dau Mot University Journal of Science - Volume 2 - Issue 1-2020 
Izhikevich E. M ., 2007; Ermentrout G. B., and Terman D. H ., 2009 ; Keener J. P., and 
Sney J., 2009 ; Murray J. D., 2010 ). It is constituted by two equations in two variables u 
and v . The first one is the fast variable called excitatory representing the transmembrane 
voltage. The second variable is the slow recovery variable describing the time dependence 
of several physical quantities, such as the electrical conductance of the ion currents across 
the membrane. The Hindmarsh-Rose equations (HR) are given by 
 du
 u f(,), u v v au32 bu I
 dt
 (1) 
 dv
 v g(,), u v c du2 v
 dt
where u corresponds to the membrane potential, v corresponds to the slow flux ions 
through the membrane, I corresponds to the applied extern current, and a,,, b c d are 
parameters. Here, I,,,, a b c d are real numbers. 
The paper is organized as follows. In section 2, a study of fixed point is investigated and 
all necessary conditions for the parameters of Hindmarsh-Rose model are found in order 
to have a stable focus. In section 3, the system undergoes subcritical Hopf bifurcation is 
shown. And finally, conclusions are drawn in Section 4. 
2. A study of fixed points 
Equilibria or stability are tools to study the dynamic of fixed points. In mathematics, a 
fixed point of a function is an element of the function's domain that is mapped to itself 
by the function. This paper focuses on the fixed points of the system (1) given by the 
resolution of the following system 
 f( u , v ) 0 v au32 bu I 0
 2
 g( u , v ) 0 v c du
It implies that 
 au32 ( d b ) u c I 0. (2) 
 db cI 
Let and  . The equation (2) can be written 
 a a
 uu32  0. 
To solve this equation, let's use the Cardan's formula after the following variables 
changes: 
 99 
Phan Van Long Em - Volume 2 - Issue 1-2020, p.98-109. 
 d b( d b )23 2( d b ) c I
 u  ,,, p q then 3 pq 0. 
 3a 3 a23 27 a a
Let now 4pq32 27 . 
If 0, then the equation (2) admits only one root and hence the system (1) admits a 
unique fixed point. Now, if 0, then the system (1) admits two fixed points, and 
finally if 0 , the system (1) admits three fixed points (see Figure 1). 
The Jacobian matrix of the system (1) is written as the following: 
 f(,)(,) u v f u v
 uv 3au2 2 bu 1
 Au(). 
 g(,)(,) u v g u v 21du
 uv
Let (uv *, *) be one fixed point of (1), we have 
 2
Det( A ( u *)  I2 )  Tr( A ( u *)) Det ( A ( u *)), 
where Tr( A ( u )) 3 au2 6 u 1 and Det( A ( u )) 3 au2 4 u . 
The reduced discriminant of Tr( A ( u )) is ' ba2 3 . If ba2 3 , then Tr( A ( u )) admits 
two real roots given by 
 b b2 3 a b D b b2 3 a b D
u and u with D b2 3. a 
 Tr1 33aaTr 2 33aa
Two roots of Det( A ( u )) is 
 ()()d b d b 2 db ()()d b d b 2
u 2 and u 0. 
 Det1 33aaDet2 3a
The nature of fixed points is rapported in Table 1. 
TABLE 1: Stability of fixed point 
If ba2 3, then Tr( A ( u )) 0 for all values of u and in this case, the fixed point is only 
stable focus or stable node. Morever, in this study, the model is needed to generate the 
 100 
 Thu Dau Mot University Journal of Science - Volume 2 - Issue 1-2020 
potential actions, it is necessary for the existence of a limit cycle. In the other word, it is 
need to have an unstable focus or a center. So the condition ba2 3 is chosen to be in 
the region IV of Table 1. The infimum and superimum in the region IV are given by 
 bD bD 
L and M . 
 3a 3a
To observe the behavior of the system (1) like Figure 1, we fix the values of parameters 
as the following a 1, b 3, c 1, d 5, I 0. Then, the system (1) becomes 
 du
 v u32 3 u
 dt
 (3) 
 dv
 15 uv2 
 dt
The system (3) has three fixed points: 
ABC ( 1.618033989, 12.090169948), ( 1, 4), (0.618033989, 0.909830058). 
In Figure 1(a), we simulated two nullclines, u 0 in red and v 0 in green. The 
intersection point of these two nullclines is three fixed points ABC,, and one orbit of 
(3) is represented in blue and it is a limit cycle. 
Figure 1: Numerical results obtained for two nullclines in green and in blue. 
The intersection points are fixed points A, B and C. The red curve is the limit cycle. 
At the point A, we get Det( A ) 1.381966013 and Tr( A ) 18.562305903, so A is a 
stable node. At the point B , we get Det( B ) 1 and Tr( B ) 10, hence B is a 
 101 
Phan Van Long Em - Volume 2 - Issue 1-2020, p.98-109. 
saddle. At the point C, we get Det( C ) 3.618033991 and Tr( C ) 1.562305899, so C 
is a instable focus. 
3. existence and direction of hopf bifurcation 
This section focuses on the existence and the direction of Hopf bifurcation, which 
corresponds to the passage of a fixed point to a limit cycle under the effect of variation 
of a parameter. Recall the Hopf's theorem (Dang-Vu Huyen, and Delcarte C., 2000). 
Theorem 1. Consider the system of two ordinary differential equations 
 u f(,,) u v a
 (4) 
 v g(,,) u v a
Let (uv *, *) a fixed point of the system (4) for all a . If the Jacobian matrix of the 
system (4) at admits two conjugate complex eigenvalues,  1,2 ()()()a a iw a 
and there is a certain value aa c such that 
  ()a
 (a ) 0, w ( a ) 0 and (a ) 0. 
 cc a c
Then, a Hopf bifurcation survives when the value of bifurcation parameter a passes by 
ac and (u *, v *, ac ) is a point of Hopf bifurcation. Moreover, let c1 in order that 
 1 2FGFFGG  2  2  2  2  2
 c1 2 2 2 2
 16w ( a )  u  u  u  u  v  u  u  v
 c (5) 
 2GGFFFGFFGG  2  2  2  2  2  3  3  3  3 
 2 2 2 2 3 2 2 3 ,
 vuvvuvvv  u  uvuvv 
where F and G are given by the method of Hassard, Kazarinoff and Wan (Dang-Vu 
Huyen, and Delcarte C., 2000). 
We can distinguish different cases 
TABLE 2: Stability of the fixed points according to Hopf bifurcation 
 c1 0 c1 0 
 stable equilibrium stable equilibrium 
 aa c 
  and no periodic orbit and unstable periodic orbit 
 (ac ) 0 
 a unstable equilibrium unstable equilibrium 
 aa 
 c and stable periodic orbit and no periodic orbit 
 102 
 Thu Dau Mot University Journal of Science - Volume 2 - Issue 1-2020 
 unstable equilibrium unstable equilibrium 
 aa c 
  and stable periodic orbit and periodic orbit 
 (ac ) 0 
 a stable equilibrium stable equilibrium 
 aa 
 c and no periodic orbit and unstable periodic orbit 
Now this theorem is applied to the Hindmarsh-Rose model in which a represents the 
bifurcation parameter 
 du
 v au32 3 u I
 dt
 (6) 
 dv
 15 uv2 
 dt
Let (uv *, *) a fixed point of the system (6). Let u u1 u* and v v1 v*, then 
 32
 ufuva1 (,,)( 1 1 vv 1 *) auu ( 1 *) 3( uu 1 *) I
 2
 v1 g(,,)15( u 1 v 1 a u 1 u *) ( v 1 v *)
With a development of the functions f and g at the neighborhood of (0,0,a ) , the 
above systems become 
 ff
 u1 u 1(0,0,) a v 1 (0,0,) a F (, u 1 v 1 ,) a
 uv11
 gg
 v u(0,0,) a v (0,0,) a G (, u v ,) a
 1 1 1 1 1
 uv11
where F(,,) u11 v a and G(,,) u11 v a are the nonlinear terms, then 
 2
 u1 ( 3 au * 6 u *) u 1 v 1 F ( u 1 , v 1 , a )
 v1 10 u * u 1 v 1 G ( u 1 , v 1 , a )
 32 2
with F( u1 , v 1 , a ) au 1 ( 3 au * 3) u 1 and G( u1 , v 1 , a ) 5 u 1 . 
Now, (0,0,a ) is a fixed point of the system. The Jacobian matrix is given by 
 3au *2 6 u * 1
A . 
 10u * 1
 103 
Phan Van Long Em - Volume 2 - Issue 1-2020, p.98-109. 
The characteristic polynomial 
 2 2 2
Det( A  I2 )  (3au * 6*1) u 3 au * 4*. u 
Let P()() a Tr A and Q()() a Det A . We get 
2 P( a ) Q ( a ) 0. 
Hence, the Jacobian matrix admits a pair of conjugate complex eigenvalues if 
 1
Det()() A Tr A 2 and the above equation has the following roots 
 4
 1,2 (a ) iw ( a ), 
 3au *2 6 u * 1
with ()a and w( a ) 3 au *22 4 u * ( a ) . 
 2
Moreover, the value ac of a , for which the real part of these eigenvalues is null, is given 
by the equations Pa(c ) 0 and Qa(c ) 0 , then 
 6u * 1 41
a and au *. 
 c 3*u 2 c 3u * 10
  3*u 2
Moreover, ().a 
 a c 2
  ()I
Thus, (a ) 0, w ( a ) 0 and (a ) 0 , then a is a bifurcation Hopf value of 
 cc a c c
the parameter a. 
In the following, the direction and the stability of Hopf bifurcation are investigated. To 
do this, let’s determine an eigenvector v1 associated with the eigenvalue 1 , obtained by 
resolving the system 
 u (1 i 10 u * 1) u v 0
(A 1 I2 ) 0 
 v 10u * u 1 i 10 u * 1 v 0
A solution of this system is an eigenvector associated with given by 
 1
V1 . 
 1 iu 10 * 1
The base change matrix is given by 
 104 
 Thu Dau Mot University Journal of Science - Volume 2 - Issue 1-2020 
 10
PVV Re(11 ) Im( ) . 
 1 10u * 1
Then 
 1 10u * 1 0
P 1 . 
 10u * 1 11
Now let the variable change 
 u1 u 2 u 2 1 u 1 
 PP . 
 v1 v 2 v 2 v 1 
Hence 
 u u u F(,,) u v a
 2 1 1 1 2 1 22
 P P AP P . 
 v 
 2 G(,,) u22 v a
 vv21 
 1 ()()a w a
Let A'( a ) P AP . Then, for aa c , it implies that 
 w()() a a
 0 wa (c ) u2 w()(,,) acc v 2 F u 2 v 2 a
Aa'(c ) 
 wa(c ) 0 
 v2 w()(,,) acc u 2 G u 2 v 2 a
with 
 F(,,) u22 v ac 1 F(,,) u22 v ac
 P . 
 G(,,) u v a 
 22c G(,,) u22 v ac
Then 
 F( u , v , a ) au32 ( 3 au * 3) u
 2 2 2 2
 1 32 
 G( u2 , v 2 , a ) au 2 (3 au * 2) u 2 
 10u * 1
Let c1 be given by the equation (5). The functions F and G depend only on u2 , the 
coefficient is given by 
 1 2FGF  2  3
c1 2(0,0, ac ) 2 (0,0, a c ) 3 (0,0, a c ). 
 16w ( ac )  u2  u 2  u 2
 105 
Phan Van Long Em - Volume 2 - Issue 1-2020, p.98-109. 
At the point (uv22 , ) (0,0) and for aa c , it implies that w( ac ) 10 u * 1 , and 
 14
c 6 a . 3 a u * 3 3 a u * 2 
 1 c16 10uu * 1 10 * 1 c c
 3 22
 6ac 3 a c u * a c u * 2 .
 4(10u * 1)
 Theorem 1 permits to deduce the direction and the stability of Hopf bifurcation from 
  
the signs of ()a and c . Now we apply this theorem in fixing all parameters values 
 a c 1
except the bifurcation parmaeter a. Let I 0, the system (6) becomes 
 du
 v au32 3 u
 dt
 (7) 
 dv
 15 uv2 
 dt
 21
The fixed points are given by resolving the equation uu32 0. 
 aa
Let 
 2 42 16 1
u  ,,, p q 
 3a 3 a23 27 a a
then 3 pq 0. Let now 4pq32 27 . We choose arbitrarily one condition 
over a, in order to have only a fixed point, it means 
 4 2 4 2 
 0 a ;  ; . 
 3 3 3 3 
With those values of a, we get 
 2
 9a 27 a22 32 27 3 a 16 3 3
ua*() 
 11 1
 3236 3a 9 a 27 a22 32 27 3 a 16 3 3
 1 11 2 1
 223 3 6 9a 27 a22 32 27 3 a 16 3 3 42 3 3 3
 .
 11 1
 3.236 3a 9 a 27 a22 32 27 3 a 16 3 3
 106 
 Thu Dau Mot University Journal of Science - Volume 2 - Issue 1-2020 
 6ua *( ) 1
Then, a . Moreover, a is solution of the equation 
 c 3ua *( )2 c
 6ua *( ) 1
 a 0. (8) 
 3ua *( )2
Figure 2: (a) The resolution of the equation (8) gives two solutions over 
 10;10 , corresponding to the intersections with the abscisses axis. (b) We are 
interested in the case where a 0, so ac 2.55165;2.5517 
The graphic resolution of the equation (8) gives two solutions over  10;10 (see Figure 
2(a)). Here, we are interested in the case where so ac 2.55165;2.5517 (see 
Figure 2(b)). With these values of ac , we get 
 112 22 5
u* 0.54 , 3 acc u * 4 u * 4.392187794 3 a u * 6 u * 1 1.526.10 . 
 10 4
 3 22
Moreover, c1 6 ac 3 a c u * a c u * 2 15.632152 0. 
 4(10u * 1)
  
So, we have ca 0, ( ) 0. From Theorem 1, 
 1 a c
 u*, v *, acc 0.54, 0.46, a 2.551655 is a Hopf bifurcation point. Moreover, for 
aa c , the fixed point is unstable with a stable periodic orbit; while for aa c , the fixed 
point is stable without periodic orbit (see Figure 3). Figure 3(a) shows the phase portrait in 
the plane (,)uv of the system (7) with a 2.54, and a stable limit cycle for a value 
aa 2.54 c . Figure 3(b) presents the time series corresponding to (,)tu . Figure 3(c) 
shows the phase portrait in the plane of the system (7) with a 2.57, and a focus 
stable for a value aI 2.57 c . Figure 3(d) presents the time series corresponding to (tu , ). 
 107 
Phan Van Long Em - Volume 2 - Issue 1-2020, p.98-109. 
Figure 3: (a) Phase portrait in the plane (,)uv of the system (7) with a 2.54, and a 
stable limit cycle for a value aa 2.54 c . (b) Time series corresponding to (,)tu . (c) 
Phase portrait in the plane of the system (7) with a 2.57, and a focus stable for a 
value aI 2.57 c . (d) Time series corresponding to 
4. Conclusion 
This work showed the necessary conditions for the parameters of Hindmarsh-Rose 
model such that there exists only a stable fixed point. It represents the resting state in 
this system. The parameter a is chosen like a bifurcation parameter, and when it crosses 
through the bifurcations values, then the equilibrium point loses its stability and 
becomes a limit cycle that implies the existence of a Hopf bifurcation. In this paper, the 
Hindmarsh-Rose model has one bifurcation value where there exists the subcritical 
Hopf bifurcation. The future work will be studied about the chaos properties in the 
Hindmarsh-Rose by adding some perturbation parameters. 
References 
Arena P., Fortuna L., Frasca M., La RosaM., (2006). Locally active Hindmarsh-Rose neurons, 
 Chaos Sol. and Fract. 27:405-412. 
Dang-Vu Huyen, and Delcarte, C., (2000). Bifurcations and Chaos, an introduction to 
 dynamicscontemporary with programs in Pascal, Fortan et Mathematica. Eds Elipses, 
 Université – Mécanique (in french). 
 108 
 Thu Dau Mot University Journal of Science - Volume 2 - Issue 1-2020 
Ermentrout, G. B., Terman, D. H., (2009). Mathematical Foundations of Neurosciences. 
 Springer. 
Hodgkin, A.L., and Huxley, A. F., (1952). A quantitative description of membrane current and 
 its application to conduction and excitation in nerve. J. Physiol. 117: 500-544. 
Izhikevich, E. M., (2007). Dynamical Systems in Neuroscience. The MIT Press. 
Keener, J. P., and Sneyd, J., (2009). Mathematical Physiology. Springer. 
Murray, J. D., (2010). Mathematical Biology. Springer. 
Nagumo, J., Arimoto, S., and Yoshizawa, S., (1962). An active pulse transmission line 
 simulating nerve axon. Proc. IRE. 50: 2061-2070. 
Nikolov S., (2005). An alternative bifurcation analysis of the Rose-Hindmarsh model, Chaos 
 Solitons and Fractal. 23:1643-1649. 
 109