A simulation of the heston model with stochastic volatility using the finite difference method

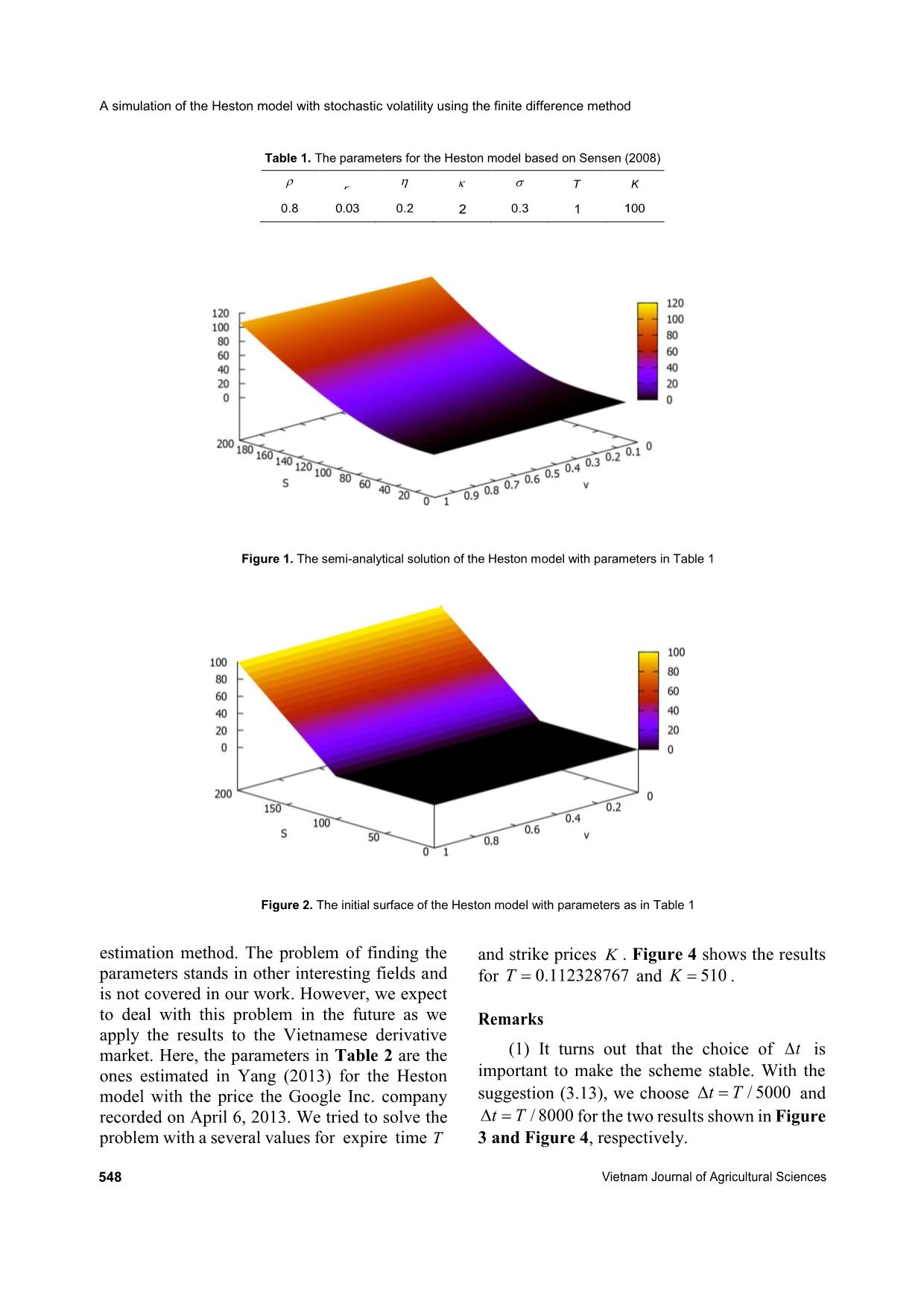
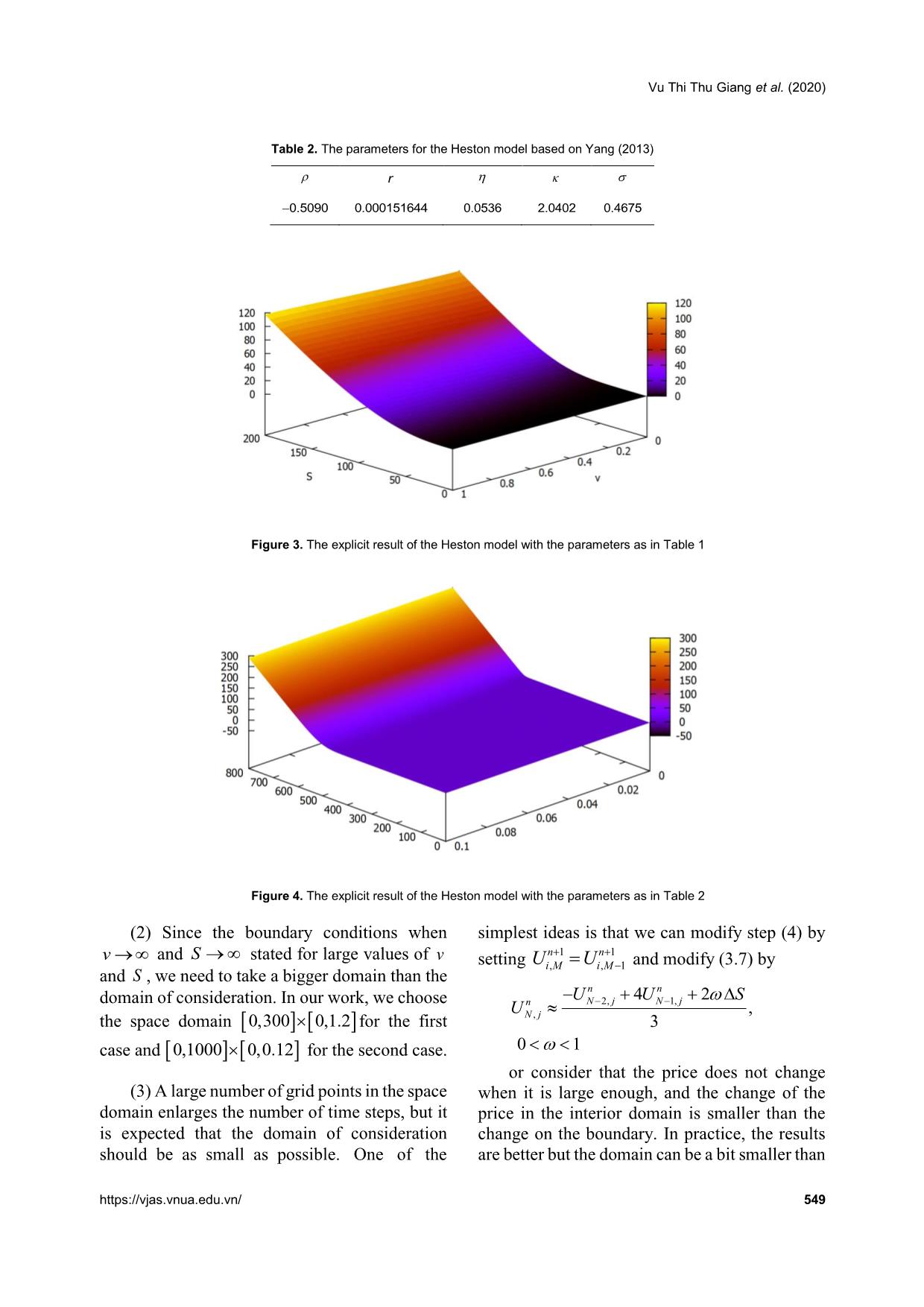
Figure 1 shows the result of the Heston The results of the explicit method are given 
solution with the parameters as in Table 1. in Figure 3 below. 
 The implementation was produced in Python Moreover, we also implement the explicit 
programming language. We have made use of the solution of the Heston model with the parameters 
Numpy and Scipy libraries together with the as presented in Table 2. 
cmath module which is very convenient when The parameters in a real model can be 
dealing with complex numbers as well as determined using market data. This work 
integration. requires a big data collection and an efficient 
https://vjas.vnua.edu.vn/ 547 
A simulation of the Heston model with stochastic volatility using the finite difference method 
 Table 1. The parameters for the Heston model based on Sensen (2008) 
    
 r T K 
 0.8 0 . 0 3 0.2 2 0.3 1 100 
 Figure 1. The semi-analytical solution of the Heston model with parameters in Table 1 
 Figure 2. The initial surface of the Heston model with parameters as in Table 1 
estimation method. The problem of finding the and strike prices K . Figure 4 shows the results 
parameters stands in other interesting fields and for T 0.112328767 and K 510 . 
is not covered in our work. However, we expect 
to deal with this problem in the future as we Remarks 
apply the results to the Vietnamese derivative 
 (1) It turns out that the choice of t is 
market. Here, the parameters in Table 2 are the 
ones estimated in Yang (2013) for the Heston important to make the scheme stable. With the 
 suggestion (3.13), we choose tT/ 5000 and 
model with the price the Google Inc. company 
recorded on April 6, 2013. We tried to solve the tT/ 8000 for the two results shown in Figure 
problem with a several values for expire time T 3 and Figure 4, respectively. 
548 Vietnam Journal of Agricultural Sciences 
 Vu Thi Thu Giang et al. (2020) 
 Table 2. The parameters for the Heston model based on Yang (2013) 
 r    
 0 . 5 0 9 0 0 . 0 0 0 1 5 1 6 4 4 0 . 0 5 3 6 2 . 0 4 0 2 0 . 4 6 7 5 
 Figure 3. The explicit result of the Heston model with the parameters as in Table 1 
 Figure 4. The explicit result of the Heston model with the parameters as in Table 2 
 (2) Since the boundary conditions when simplest ideas is that we can modify step (4) by 
v and S stated for large values of v nn 11
 setting UUi,,1 Mi M and modify (3.7) by 
and S , we need to take a bigger domain than the 
 nn
domain of consideration. In our work, we choose UUSN 2,1, jN42 j 
 U n ,
the space domain 0,300  0,1.2for the first Nj, 3 
case and 0,10000,0.12 for the second case. 01 
     
 or consider that the price does not change 
 (3) A large number of grid points in the space when it is large enough, and the change of the 
domain enlarges the number of time steps, but it price in the interior domain is smaller than the 
is expected that the domain of consideration change on the boundary. In practice, the results 
should be as small as possible. One of the are better but the domain can be a bit smaller than 
https://vjas.vnua.edu.vn/ 549 
A simulation of the Heston model with stochastic volatility using the finite difference method 
the original treatment. In our result, we choose and v . To obtain a better error, we extend 
 0.9 , which says that the change of the price the domain of consideration to
in the interior domain is “a bit” smaller than the (,)0,3000,1.2Sv    . The results are given in 
change on the boundary. Table 5 below. 
 All the numerical solutions are implemented From the tables, we can see that the scheme 
in Python language with the help of the Numpy has a smaller error when the size of the domain 
library, which provides a very powerful increases. We also can see that the error is getting 
environment to work with arrays and vectors. smaller as time step t 0 but the process is 
Note that since the coefficients (3.3), (3.7), and slow (first-order in time). On the other hand, the 
(3.11) are independent of the time t , we compute convergence is much faster when the space steps 
them outside the time loop and employ a lower tend to 0 (second-order in space). However, if we 
computation time. take the space steps smaller, we need to take the 
 time step extremely small due to the stability 
Comparisons condition. It is a main problem of the explicit 
 We will take the Heston solution as the method in spite of its simplicity. As seen in 
reference solution to compare. Let us take the Table 5, with the extension domain, we need to 
first case to look at the errors in more detail. 1
 take the time step from t . 
Figure 5 below shows the price surfaces given 7000
by both the Heston formula and the explicit 
 If we use a modification by setting 
scheme in the same coordinate system. The nn 11
colored surface represents the explicit result, UUiMiM,,1 and 
while the green mesh represents the Heston UUSnn42
solution. U n NjNj 2,1, , 01,  we 
 Nj, 3
 We also cut through the surfaces by the plane 
 can consider a much smaller extension domain of 
v 1 to see the differences between two graphs 
as shown in Figure 6, where the higher green S as S 0,225 . As can be seen in Table 6, we 
graph represents the explicit result and the lower obtain a smaller error in comparison with the 
purple graph represents the Heston solution. ones in Table 5. Moreover, the time steps t are 
Figure 6 shows a small difference between the 1
 much smaller, starting from t . Indeed, 
Heston solution and the explicit solution. 2000
 It is easy to see that the time step size t we can use the time steps as in Table 4. 
strongly impacts the result. When t is big, the 
 Therefore, our modification helps to reduce 
scheme is unstable, and the error blows up as the size of the S domain as well as the number 
shown in Table 3. In contrast, when t is small 
 of time steps, which gives a lower computational 
enough, the scheme seems stable with the error cost. The results are also better in the sense that 
as illustrated in Table 4. the errors are reduced. 
 However, even though we expected that the We also tried the Heston model with 
error tends to 0 as t 0 , it seems that the different parameters. Following Yang (2013), 
convergence is very slow and the error has small with the data of Google Inc., the parameters for 
 1 the Heston model are chosen as in Table 2. 
differences when t varies from to 
 1500 Table 7 below gives the results at the spot price 
 S 783.05 and the variance v 0.069545829 . 
 1 Error 
 . The relative error is given by L . We compare the data at different values of expire 
 20000 U 
 L time T and strike price K . The relative error 
 As mentioned in the previous section, we here is computed by 
 Explicit Heston price - Google Inc. Price.
need to use a bigger domain than the original one Error = . 
to cover the boundary condition when S Google Inc. Price
550 Vietnam Journal of Agricultural Sciences 
 Vu Thi Thu Giang et al. (2020) 
 Figure 5. The Heston solution and the explicit solution of the Heston model with parameters as in Table 1. 
 Figure 6. The cut at v 1 of the surfaces in Figure 5. 
 Table 3. The L error when the scheme is unstable 
 t Error (in L norm) 
 1
 8.33.10136 
 500
 1
 4.08.10279 
 1000
 1
 11.126266 
 1200
 We denote the explicit Heston price by applied efficiently to the Heston model with 
H price . We can see that the scheme can be different kinds of parameters. 
https://vjas.vnua.edu.vn/ 551 
A simulation of the Heston model with stochastic volatility using the finite difference method 
Table 4. The L error and the relative error when the scheme is stable, with S 5, v 0.05,( S , v )  0,200  0,1
 t Error (in L norm) Relative Error 
 1
 1 1 . 1 2 5 4 6 3 1 0 . 4 6 5 9 %
 1500 
 1
 1 1 . 1 2 3 8 5 6 1 0 . 4 6 4 4 %
 3000 
 1
 1 1 . 1 2 3 2 0 8 1 0 . 4 6 3 8 %
 4500 
 1
 1 1 . 1 2 3 0 5 3 1 0 . 4 6 3 6 %
 6000 
 1
 1 1 . 1 2 2 4 9 1 1 0 . 4 6 3 1 %
 20000 
Table 5. The L error and the relative error when the scheme is stable, with SvS5,0.05, v (,)0,3000,1.2    
 t Error (in L norm) Relative Error 
 1
 5 . 9 5 7 4 8 3 1 3 5 . 6 0 4 3 %
 7000 
 1
 5 . 9 5 7 5 3 4 1 9 5 . 6 0 4 4 %
 10000 
 1
 5.95753075 5.6043%
 20000 
Table 6. The L error and the relative error when the modification scheme is stable, with SvS5,0.05, v ( , )0,2250,1.2    
 t Error (in L norm) Relative Error 
 1
 4.325400 4.6090%
 2000 
 1
 4.325450 4.6090%
 3000 
 1
 4.325489 4.6091%
 5000 
Table 7. A comparison between the explicit solution of the Heston model with the parameters as in Table 2 and the data of Google 
Inc. at the spot price S 783.05 and the variance v 0.069545829 
 Google Inc. 
 Expire time T Strike price K H - price Error (%) 
 price 
 0.112328767 510 272.90 272.5087508 0.1539 
 0.112328767 590 193.25 192.5350415 0.3699 
 0.457534247 395 388.30 387.5296684 0.1983 
 0.457534247 410 373.40 372.5333392 0.2320 
 0.783561644 395 389.70 387.5881280 0.5419 
 0.783561644 410 375.00 372.6184232 0.6350 
552 Vietnam Journal of Agricultural Sciences 
 Vu Thi Thu Giang et al. (2020) 
Conclusions Heston S. (1993). A closed‐form solution for options with 
 stochastic volatility. The Review of Financial Studies. 
 In our work, the explicit finite difference 6: 327-343. 
scheme with some simple modifications on the Heston S. (1997). A simple new formula for options with 
boundaries have been applied to the Heston stochastic volatility. Working paper. Olin J. M. School 
pricing model with European options. Our results of Business. Washington University. 
show that the explicit scheme with the Hout K. J. in ’t (2007). ADI schemes in the numerical 
 solution of the Heston PDE. Numerical Analysis and 
modifications is simple, easy to apply, and gives Applied Mathematics. AIP Conference Proceedings. 
a better approximation to the Heston solution in 936: 10-14. DOI: 10.1063/1.2790085 
comparison with the classical method. However, Hull J. C. & White A. (1987). The pricing of options on 
the scheme still has the disadvantage of stability assets with stochastic volatility. Journal of Finance. 
conditions. To overcome this disadvantage, some 42: 281‐300. 
authors developed the alternative direction Hull J. C. (2012). Options, futures and other derivatives 
 (8th ed.). Prentice-Hall. Upper Saddle River. 
implicit (ADI) scheme, which is a kind of mixed 
 Hundsdorfer W. (2002). Accuracy and stability of splitting 
explicit-implicit scheme. The ADI scheme is with Stabilizing Corrections. Applied Numerical 
unconditionally stable. Nevertheless, it is more Mathematics. 42: 213‐233. 
complicated in comparison with the explicit Kahl C. & Jäckel P. (2006). Fast strong approximation 
method. Furthermore, the ADI scheme must be Monte Carlo schemes for stochastic volatility models. 
used with care since a high dimensional matrix Quantitative Finance. 6: 513-536. 
 Lewis A. (2000). Option Valuation under Stochastic 
appears in a linear system of equations and an Volatility: With Mathematica Code. Finance Press. 
efficient solver is needed. In future work, we Newport Beach. 
expect to apply this method in an efficient way to Li H. & Huang Z. (2020) An iterative splitting method for 
the Heston model with more complicated options pricing European options under the Heston model. 
types such as the American option and Barrier Applied Mathematics and Computation. DOI: 
 10.1016/j.amc.2020.125424. 
option. Besides, the parameter estimation and the 
 Lord R. & Kahl C. (2007). Optimal Fourier Inversion in 
application of this scheme in the Vietnamese Semi-Analytical Option Pricing. Tinbergen Institute 
derivative market is also a problem of interest. Discussion Paper 2006-066(2). Retrieved from 
 https://ssrn.com/abstract=921336 or 
  on September 
References 20, 2019. 
 Lord R., Koekkoek R. & van Dijk D. (2010). A comparison 
Bates D. S. (1996). Jumps and stochastic volatility: of biased simulation schemes for stochastic volatility 
 Exchange rate processes implicit in Deutsche Mark models. Quantitative Finance. 10: 177-194. 
 options. Review of Financial Studies. 9(1): 69-107. 
 Merton R. (1973). The theory of rational option pricing. 
Black F. & Scholes M. (1973). The Pricing of Options and Bell Journal of Economics and Management Science. 
 Corporate Liabilities. Journal of Political Economy. 4: 141-183. 
 81(3): 637-654. 
 Merton R. (1976). Option pricing when underlying stock 
Chen X., Burkardt J. & Gunzburger M. (2014). High returns are discontinuous. Journal of Financial 
 accuracy finite element methods for option pricing Economics. 3: 125-144. 
 under Heston’s stochastic volatility model. Florida Peaceman D. W. & Rachford H. H. (1955). The numerical 
 State University. solution of parabolic and elliptic differential equations. 
Craig I. J. D. & Sneyd A. D. (1988). An alternating‐ Journal of the Society for Industrial and Applied 
 direction implicit scheme for parabolic equations with Mathematics. 3: 28‐41. 
 mixed derivatives. Computer & Mathematics with Rouah F. D. (2013). The Heston Model and Its Extensions 
 Applications. 16(4): 341-350. in Matlab and C#. John Wiley & Sons, Ltd. 
Douglas J. & Rachford H. H. (1956). On the numerical Safaei M., Neisy A. & Nematollahi N. (2018). New 
 solution of heat conduction problems in two and three splitting scheme for pricing American options under 
 space variables. Transactions of the American the Heston model. Computational Economics. 52(2): 
 Mathematical Society. 82: 421‐439. 405-420. 
During B. & Miles J. (2017). High-order ADI scheme for Schmelzle M. (2010). Option pricing formulae using 
 option pricing in stochastic volatility models. Journal of Fourier transform: Theory and application. Working 
 Computational and Applied Mathematics. 316:109-121. paper. Retrieved from 
https://vjas.vnua.edu.vn/ 553 
A simulation of the Heston model with stochastic volatility using the finite difference method 
 https://pfadintegral.com/docs/Schmelzle2010%20Fou Thomas J. W. (1995). Numerical Partial Differential 
 rier%20Pricing.pdf on September 25, 2019. Equations: Finite Difference Methods. New York, 
Sensen L. (2008). Finite Difference Schemes for Heston Springer-Verlag. 
 Model. Thesis. Retrieved from Winkler G., Apel T. & Wystup U. (2001). Valuation of options 
 https://core.ac.uk/download/pdf/97116.pdf on in Heston’s stochastic volatility model using finite 
 January 10, 2019. element methods. Foreign Exchange Risk. 283-303. 
Stein E. M. & Stein J. C. (1991). Stock price distributions Yang Y. (2013). Valuing a European option with the 
 with stochastic volatility: an analytic approach. Heston model. Master’s Thesis. Rochester Institute of 
 Review of Financial Studies. 4(4): 727-752. Technology. 
554 Vietnam Journal of Agricultural Sciences