A novel cryptosystem using dynamics perturbation of logistic map

�−1 to make 𝐶𝐶𝑋𝑋𝑋𝑋 delayed 
for calculating the future pixel. The value of 
𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) becomes 
𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵𝐵(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) = � 𝐶𝐶0 for 𝑛𝑛(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) = 1 and 𝑝𝑝(𝑥𝑥, 𝑦𝑦) with 𝑥𝑥 = 0 and 𝑦𝑦 = 0𝐶𝐶𝑋𝑋𝑋𝑋−1 for 𝑛𝑛(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) = 1 and 𝑝𝑝(𝑥𝑥, 𝑦𝑦) with 𝑥𝑥 ≠ 0 or 𝑦𝑦 ≠ 0
𝐵𝐵𝐵𝐵𝐵𝐵𝐸𝐸𝑥𝑥𝐵𝐵𝑟𝑟(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) for 1 < 𝑛𝑛(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) ≤ 𝑁𝑁(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) and 𝑝𝑝(𝑥𝑥, 𝑦𝑦) with ∀𝑥𝑥,𝑦𝑦 . 
(8) 
The constraint for the number of bits in the 
cryptosystem will be considered. 
Fig. 3. Structure of iCD. 
Journal of Science & Technology 139 (2019) 024 - 030 
27 
3. Simulation results 
In order to illustrate the operation of the 
cryptosystem, the example is simulated for 8 bits gray 
scale images with the size of 256 × 256, or 𝑘𝑘1 =log2 256 × 256 = 16 bits and 𝑘𝑘2 = 8 bits. Tables 1 
and 2 show the number of bits and the chosen value 
for parameters, respectively. 
Table 1. The number of bits representing for data. 
Parameters #bits Fixed point format 
𝑚𝑚1 32 1.31 
𝑚𝑚2 33 2.31 
Table 2. The value of parameters and number of bits 
for representation. 
Parameters Chosen value Represented by #bits 
𝑟𝑟(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝) 3.625 33 
𝑟𝑟(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) 3.625 33 
𝐼𝐼𝑉𝑉(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝) 0.0123456789 32 
𝐼𝐼𝑉𝑉(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) 0.9876543210 32 
𝐶𝐶0 123 8 
Total no. of bits 138 
The value of other parameters for the simulation is 
𝑁𝑁(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) = 1, 𝑁𝑁 = 1, 𝑛𝑛 = 1, and 𝑚𝑚 = 1. 
In order to guarantee the chaotic behavior 
exhibited by the Logistic map, 
𝑟𝑟(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝) = 𝑟𝑟(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) = 3.625 is chosen, so its binary 
representation is 111010000000000000000000000000000. The bit 
positions in 𝑟𝑟(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝) and 𝑟𝑟(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) to be perturbed to 
produce 𝑟𝑟 are from 𝑏𝑏0 to 𝑏𝑏28. As a result, the value 
range of 𝑟𝑟 for the Logistic map in both the CPP and 
the CD is from 3.625 to 3.99999 (2−31 less than 4.0). 
The extension functions 𝑓𝑓1(. ) and 𝑓𝑓3(. )are filled 
zeros to the bit positions rather than those indicated in 
𝑄𝑄1
(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝) and 𝑄𝑄1(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑). Moreover, the extraction 
functions 𝑓𝑓2(. ) and 𝑓𝑓4(. ) collect bits from 𝑋𝑋𝑛𝑛 with the 
order of bits defined in 𝑄𝑄2
(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝) and 𝑄𝑄2(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑). 
It is noted that the order of bits specified by 
𝑄𝑄1
(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝), 𝑄𝑄1(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑), 𝑄𝑄2(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝), and 𝑄𝑄2(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) will make the 
key space expanded significantly. In this example, the 
sizes are �𝑄𝑄1
(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝)� = 16, �𝑄𝑄1(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑)� = 8, �𝑄𝑄2(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝)� =16, and �𝑄𝑄2(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑)� = 8. The chosen order is displayed 
in Table 3. 
Table 3. The order of bits. 
The 
lists The order of bits 
𝑄𝑄1
(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝) {2,9,13,1,10,8,5,12,3,14,7,15,4,0,6,11} 
𝑄𝑄2
(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝) {3,14,6,15,10,8,4,12,13,11,7,1,5,0,2,9} 
𝑄𝑄1
(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) {7,1,3,6,4,5,2,0} 
𝑄𝑄2
(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) {2,5,6,0,4,3,7,1} 
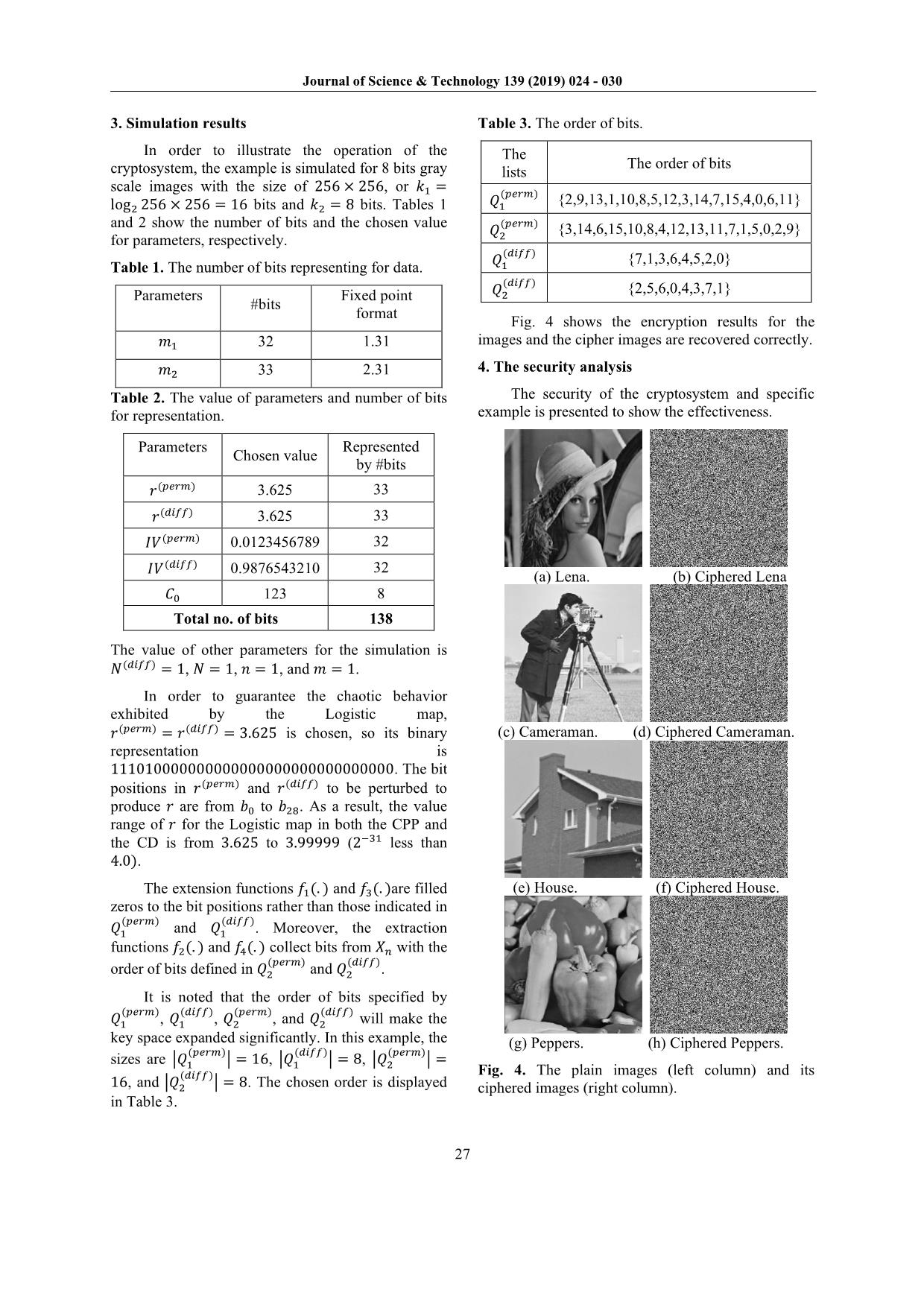
Fig. 4 shows the encryption results for the 
images and the cipher images are recovered correctly. 
4. The security analysis 
The security of the cryptosystem and specific 
example is presented to show the effectiveness. 
(a) Lena. (b) Ciphered Lena 
(c) Cameraman. (d) Ciphered Cameraman. 
(e) House. (f) Ciphered House. 
(g) Peppers. (h) Ciphered Peppers. 
Fig. 4. The plain images (left column) and its 
ciphered images (right column). 
Journal of Science & Technology 139 (2019) 024 - 030 
28 
4.1. The key space 
The rule of bits to be extracted and extended in 
the permutation and diffusion can be considered as 
the contribution to the key space. As shown in this 
example with the value 𝑟𝑟(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝) = 𝑟𝑟(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) = 3.625, 
these are represented in the format of fixed point as 111010000000000000000000000000000. So the 
number of bits can be perturbed is 29 bits for each of 
control parameters in this example. There is a number 
of possible ways of extension for 𝑘𝑘1 and 𝑘𝑘2 bits laid 
out of 29 bits in the permutation and the diffusion 
processes. Moreover, the same number of possible 
ways of extraction for bits to get pixel positions 
𝑋𝑋𝑋𝑋𝑛𝑛𝑛𝑛𝑛𝑛 and the value of cipher pixels 𝐶𝐶𝑋𝑋𝑋𝑋 from 𝑋𝑋𝑛𝑛. 
The location information for the extraction and 
extension is considered as the encryption key of the 
proposed cryptosystem. That is presented by the 
value of elements in 𝑄𝑄1
(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝), 𝑄𝑄1(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑), 𝑄𝑄2(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝), and 
𝑄𝑄2
(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑). The values of the bit order can be ranged 
from 0 to 30, so, each element is encoded by 5 bits. It 
is noted that each elements of 𝑄𝑄1
(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝), and 𝑄𝑄2(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝) 
has 16 elements and each element represented by 5 
bits, while each elements of 𝑄𝑄1
(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑)and 𝑄𝑄2(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑)has 8 
elements and each is encoded by 5 bits. The total 
number of bits represents for the order of bits 𝑁𝑁𝑜𝑜𝑝𝑝𝑑𝑑𝑛𝑛𝑝𝑝 
in 𝑄𝑄1
(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝), 𝑄𝑄1(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑), 𝑄𝑄2(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝), and 𝑄𝑄2(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑)is 𝑁𝑁𝑜𝑜𝑝𝑝𝑑𝑑𝑛𝑛𝑝𝑝 =5 × (2 × 16 + 2 × 8) = 240 bits. As given in Table 
2, the number of bits representing for parameters is 
𝑁𝑁𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 = 138. Therefore, the key space is 𝑁𝑁𝑆𝑆𝑝𝑝𝑝𝑝𝑆𝑆𝑛𝑛 =
𝑁𝑁𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 + 𝑁𝑁𝑜𝑜𝑝𝑝𝑑𝑑𝑛𝑛𝑝𝑝(= 378 bits in this case). 
It is clear that the key space 𝑁𝑁𝑆𝑆𝑝𝑝𝑝𝑝𝑆𝑆𝑛𝑛is expanded 
more much significantly in compared with that in the 
case of without considering the rule of bits to be 
extracted and extended. 
4.2. The key sensitivity analysis 
The key sensitivity analysis is considered by 
means of the difference in ciphertexts obtained by 
smallest difference in encryption keys [8]. Let us call 
Δ𝐾𝐾 be the tolerance in the encryption key. The 
ciphertext difference rate (𝐶𝐶𝐶𝐶𝑟𝑟) is reflected for the 
key sensitivity and calculated by 
𝐶𝐶𝐶𝐶𝑟𝑟 = 𝐷𝐷𝑑𝑑𝑑𝑑𝑑𝑑(𝐶𝐶,𝐶𝐶1)+𝐷𝐷𝑑𝑑𝑑𝑑𝑑𝑑(𝐶𝐶,𝐶𝐶2)
2𝑀𝑀×𝑁𝑁 × 100%. (9) 
𝑀𝑀 and 𝑁𝑁 are the number of pixel rows and 
columns; 𝐶𝐶 is the ciphertext using the encryption key 
𝐾𝐾; 𝐶𝐶1 and 𝐶𝐶2are ciphertexts using the encryption key 
𝐾𝐾 + Δ𝐾𝐾 and 𝐾𝐾 − Δ𝐾𝐾, respectively. There, 
𝐷𝐷𝐵𝐵𝑓𝑓𝑓𝑓(𝐴𝐴,𝐵𝐵) is the number of pixels with the value in 
𝐴𝐴 different from that in 𝐵𝐵, i.e. 
𝐷𝐷𝐵𝐵𝑓𝑓𝑓𝑓(𝐴𝐴,𝐵𝐵) = ∑ ∑ 𝐷𝐷𝐵𝐵𝑓𝑓𝑝𝑝(𝐴𝐴(𝑥𝑥,𝑦𝑦),𝐵𝐵(𝑥𝑥,𝑦𝑦))𝑁𝑁−1𝑦𝑦=0𝑀𝑀−1𝑥𝑥=0 , 
(10) 
where 𝐷𝐷𝐵𝐵𝑓𝑓𝑝𝑝(𝐴𝐴(𝑥𝑥,𝑦𝑦),𝐵𝐵(𝑥𝑥,𝑦𝑦)) is 
𝐷𝐷𝐵𝐵𝑓𝑓𝑝𝑝�𝐴𝐴(𝑥𝑥, 𝑦𝑦),𝐵𝐵(𝑥𝑥,𝑦𝑦)� = �1, for 𝐴𝐴(𝑥𝑥,𝑦𝑦) ≠ 𝐵𝐵(𝑥𝑥,𝑦𝑦);0, for 𝐴𝐴(𝑥𝑥, 𝑦𝑦) = 𝐵𝐵(𝑥𝑥,𝑦𝑦). 
(11) 
The simulation is carried out with smallest 
difference in every single element contributing to the 
encryption key, i.e. 𝑟𝑟(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝), 𝑟𝑟(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑), 
𝐼𝐼𝑉𝑉(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝), 𝐼𝐼𝑉𝑉(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑), and 𝐶𝐶0. The smallest amount of 
tolerance Δ𝐾𝐾 is defined by the resolution of the value 
representation, i.e. one bit of LSB. The value of other 
parameters is as chosen earlier. In addition, the 
simulation performs on a set of 100 random images 
with the same size of 256 × 256. The means and 
standard deviation of 𝐶𝐶𝐶𝐶𝑟𝑟 is as shown in Table 4. 
Table 4. The key sensitivity 𝐶𝐶𝐶𝐶𝑟𝑟. 
On 
parameter
s 
𝐶𝐶𝐶𝐶𝑟𝑟 
Mean (%) Std. dev. (%) 
𝑁𝑁𝑝𝑝𝑜𝑜𝑟𝑟𝑛𝑛𝑑𝑑 1 2 3 1 2 3 
𝑟𝑟(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝) 99.8 99.9 99.9 0.015 0. 01 0.01 
𝑟𝑟(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) 99.7 99.8 99.8 0.02 0.02 0.01 
𝐼𝐼𝑉𝑉(𝑝𝑝𝑛𝑛𝑝𝑝𝑝𝑝) 98.6 98.8 99.0 0.012 0.01 0.01 
𝐼𝐼𝑉𝑉(𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑) 98.9 98.9 99.0 0.02 0.015 0.01 
𝐶𝐶0 99.0 99.4 99.5 0.021 0.02 0.01 
It is clear from Table 4 that the rate of change is 
very large and it seems to need a single encryption 
round to get the value of almost pixels changed. The 
maximum value of 𝐶𝐶𝐶𝐶𝑟𝑟 is 99.9% at the third round is 
much better than that of 99.63% as the result of work of 
[10] published very recently. 
4.3. Information entropy analysis 
In this work, the well-known Shannon’s 
information entropy is applied to measure the 
randomness in the data of cipher images. The 
information entropy (IE) is 
𝐼𝐼𝐸𝐸(𝑚𝑚) = ∑ 𝑝𝑝(𝑚𝑚𝑑𝑑) log2 1𝑝𝑝(𝑝𝑝𝑖𝑖)2𝑘𝑘2−1𝑑𝑑=0 , (12) 
where 𝑘𝑘2 is the number of bits representing for the 
pixel value; 𝑚𝑚𝑑𝑑 is the value of pixels; and 𝑝𝑝(𝑚𝑚𝑑𝑑)is the 
probability of 𝑚𝑚𝑑𝑑 occcurence. In this work, four well-
known grayscale images with the size of 256 × 256 
are used for measuring 𝐼𝐼𝐸𝐸 of the cipher images, i.e. 
Lena, Cameramen, House, and Peppers. The 𝐼𝐼𝐸𝐸 with 
respect for a number of encryption rounds is obtained 
as given in Table 5. Specifically, the value of 𝐼𝐼𝐸𝐸 =7.999 is almost equal to the theoritical value of 8. It 
is much better than that most of recent results, i.e. 
7,9972 in [11], 7,9974 in [12], and 7,9965 in [9], etc. 
Journal of Science & Technology 139 (2019) 024 - 030 
29 
Table 5. The IE of the ciphered image. 
Name IE 
𝑁𝑁𝑝𝑝𝑜𝑜𝑟𝑟𝑛𝑛𝑑𝑑 1 2 3 
Lena 7.990 7.990 7.998 
Cameraman 7.980 7.990 7.999 
House 7.970 7.989 7.999 
Peppers 7.985 7.987 7.999 
4.4. Differential analysis 
The differential analysis is to test the 
cryptosysem against from differential attacks by 
using the slightly difference in the plaintexts with 
respect to that in the corresponding ciphertexts. Here, 
the analysis for the differential attack is based on the 
two well-known measures, i.e. Number of Pixels 
Change Rate (NPCR) and Unified Average Changing 
Intensity (UACI). The equation to calculate 𝑁𝑁𝑃𝑃𝐶𝐶𝑁𝑁 
and 𝑈𝑈𝐴𝐴𝐶𝐶𝐼𝐼 are as below. 
𝑁𝑁𝑃𝑃𝐶𝐶𝑁𝑁 = ∑ 𝐷𝐷(𝑥𝑥,𝑦𝑦)𝑥𝑥,𝑦𝑦
𝑀𝑀×𝑁𝑁 × 100%, (13) 
𝑈𝑈𝐴𝐴𝐶𝐶𝐼𝐼 = 1
𝑀𝑀×𝑁𝑁 ∑ |𝐶𝐶1(𝑥𝑥,𝑦𝑦)−𝐶𝐶2(𝑥𝑥,𝑦𝑦)|𝑥𝑥,𝑦𝑦 255 × 100%, (14) 
𝐷𝐷(𝑥𝑥, 𝑦𝑦) = �1, 𝑓𝑓𝑓𝑓𝑟𝑟 𝐶𝐶1(𝑥𝑥, 𝑦𝑦) ≠ 𝐶𝐶2(𝑥𝑥, 𝑦𝑦)0, 𝑓𝑓𝑓𝑓𝑟𝑟 𝐶𝐶1(𝑥𝑥, 𝑦𝑦) = 𝐶𝐶2(𝑥𝑥, 𝑦𝑦). (15) 
There, 𝐶𝐶1(𝑥𝑥, 𝑦𝑦)and 𝐶𝐶2(𝑥𝑥, 𝑦𝑦) are pixels at the 
location (𝑥𝑥,𝑦𝑦) in the cipher images with a slightly 
difference in their corresponding plain images. 
In this work, a set of 100 plain images with the 
random value of pixels and the size of 256 × 256 are 
used. Encryption is carried out with the set of plain 
images 𝑃𝑃1 to produce a set of cipher images 𝐶𝐶1. The 
slightly difference is made to each of images in 𝑃𝑃 to 
get 𝑃𝑃2 . A modification with randomly increased or 
decreased by 1 to the value of randomly chosen pixel, 
except for the pixels with the value of 0 and 255. 
Then, images in 𝑃𝑃2 are encrypted with different 
encryption rounds (𝑁𝑁𝑝𝑝𝑜𝑜𝑟𝑟𝑛𝑛𝑑𝑑) to produce a set of cipher 
images 𝐶𝐶2. Calculation for 𝑁𝑁𝑃𝑃𝐶𝐶𝑁𝑁 and 𝑈𝑈𝐴𝐴𝐶𝐶𝐼𝐼 is 
performed on 𝐶𝐶1and 𝐶𝐶2. 
The average of 𝑁𝑁𝑃𝑃𝐶𝐶𝑁𝑁 and 𝑈𝑈𝐴𝐴𝐶𝐶𝐼𝐼 as well as the 
standard deviation are calculated over the set of 100 
images as described. The result is shown in Table 6 
that the 𝑁𝑁𝑃𝑃𝐶𝐶𝑁𝑁 and 𝑈𝑈𝐴𝐴𝐶𝐶𝐼𝐼 of proposed cryptosystem is 
as good as those in the recent results published by in 
[9,10] and better than those cited therein. 
Table 6 shows that the maximum NPCR and UACI are 99.9 and 33.451, respectively. The result of NPCR in this work is better that that of 99.6126 in [9], 
of 99.61 in [10], and of 99.5974 in [13], etc. 
Table 6. The average of 𝑁𝑁𝑃𝑃𝐶𝐶𝑁𝑁 and 𝑈𝑈𝐴𝐴𝐶𝐶𝐼𝐼 calculated 
over 100 pixels. 
𝑁𝑁𝑝𝑝𝑜𝑜𝑟𝑟𝑛𝑛𝑑𝑑 
𝑁𝑁𝑃𝑃𝐶𝐶𝑁𝑁 (%) 𝑈𝑈𝐴𝐴𝐶𝐶𝐼𝐼 (%) 
Mean Std. dev. Mean Std. dev. 
1 99.6 0.030 33.451 0.020 
2 99.8 0.012 33.450 0.015 
3 99.9 0.010 33.430 0.011 
5. Conclusion and future works 
The paper has presented the novel cryptosystem 
using the Logistic map. The main contribution of this 
work is that the cryptosystem works on the bit level 
perturbation on the control parameter of the Logistic 
map. The key space is 378 bits and this is very large 
in compared with other cryptosystems. With this key 
space, the brute-force attack must be unsuccessful on 
nowadays computers. The simulation results also 
show that the proposed cryptosystem can be as good 
as those published recently. 
The future work will be the investigation for the 
bit level perturbation on chaotic values of state 
variables, and for the implementation them on the 
reconfigurable hardware. 
Acknowledgments 
This research is funded by Vietnam National 
Foundation for Science and Technology 
Development (NAFOSTED) under grant number 
102.04-2018.06. 
References 
[1] L. Kocarev, S. Lian, Chaos-Based Cryptography: 
Theory, Algorithms and Applications, Springer Berlin 
Heidelberg (2011). 
[2] L. Kocarev, Chaos-based cryptography: a brief 
overview, IEEE Circuits and Systems Magazine 1 
(2001) 6-21. 
[3] G. Alvarez, S. Li, Some basic cryptographic 
requirements for chaos-based cryptosystems, 
International Journal of Bifurcation and Chaos 16 
(2006) 2129-2151. 
[4] S.E. Assad, M. Farajallah, A new chaos-based image 
encryption system, Signal Processing: Image 
Communication 41 (2016), 144-157. 
[5] L. Liu, S. Miao, A new image encryption algorithm 
based on logistic chaotic map with varying parameter, 
SpringerPlus 5 (2016) 289. 
[6] W. Zhang, K-W. Wong, H. Yu, Z-L. Zhu, A 
symmetric color image encryption algorithm using 
the intrinsic features of bit distributions, 
Communications in Nonlinear Science and Numerical 
Simulation 18 (2013) 584-600. 
Journal of Science & Technology 139 (2019) 024 - 030 
30 
[7] J. Chen, Z. Zhu, C. Fu, L. Zhang, Y. Zhang, An 
image encryption scheme using nonlinear inter-pixel 
computing and swapping based permutation 
approach, Communications in Nonlinear Science and 
Numerical Simulation 23 (2015) 294 – 310. 
[8] S. Lian, J. Sun, Z. Wang, Security Analysis of A 
Chaos-based Image Encryption Algorithm, Physica 
A. 351 (2005) 645 - 661. 
[9] P. Ping, J. Fan, Y. Mao, F. Xu, J. Gao, A chaos based 
image encryption scheme using digit-level 
permutation and block diffusion, IEEE Access. 6 
(2018) 67581 - 67593. 
[10] Erdem Yavuz, A novel chaotic image encryption 
algorithm based on content-sensitive dynamic 
function switching scheme, Optics & Laser 
Technology 114 (2019), 224-239. 
[11] Y. Li, C. Wang, and H. Chen, A hyper-chaos-based 
image encryption algorithm using pixel-level 
permutation and bit-level permutation, Optics and 
Lasers in Engineering 90 (2017), 238 – 246. 
[12] X.Wang and H. li Zhang, A color image encryption 
with heterogeneous bit permutation and correlated 
chaos, Optics Communications 342 (2015), 51– 60. 
[13] A.-V. Diaconu, Circular inter-intra pixels bit-level 
permutation and chaos based image encryption, 
Information Sciences 355-356 (2016), 314 – 327.