Xây dựng mô hình tính toán độ phụ thuộc vào lưới của hệ thống năng lượng mặt trời/battery dựa trên tổng lượng bức xạ hàng năm

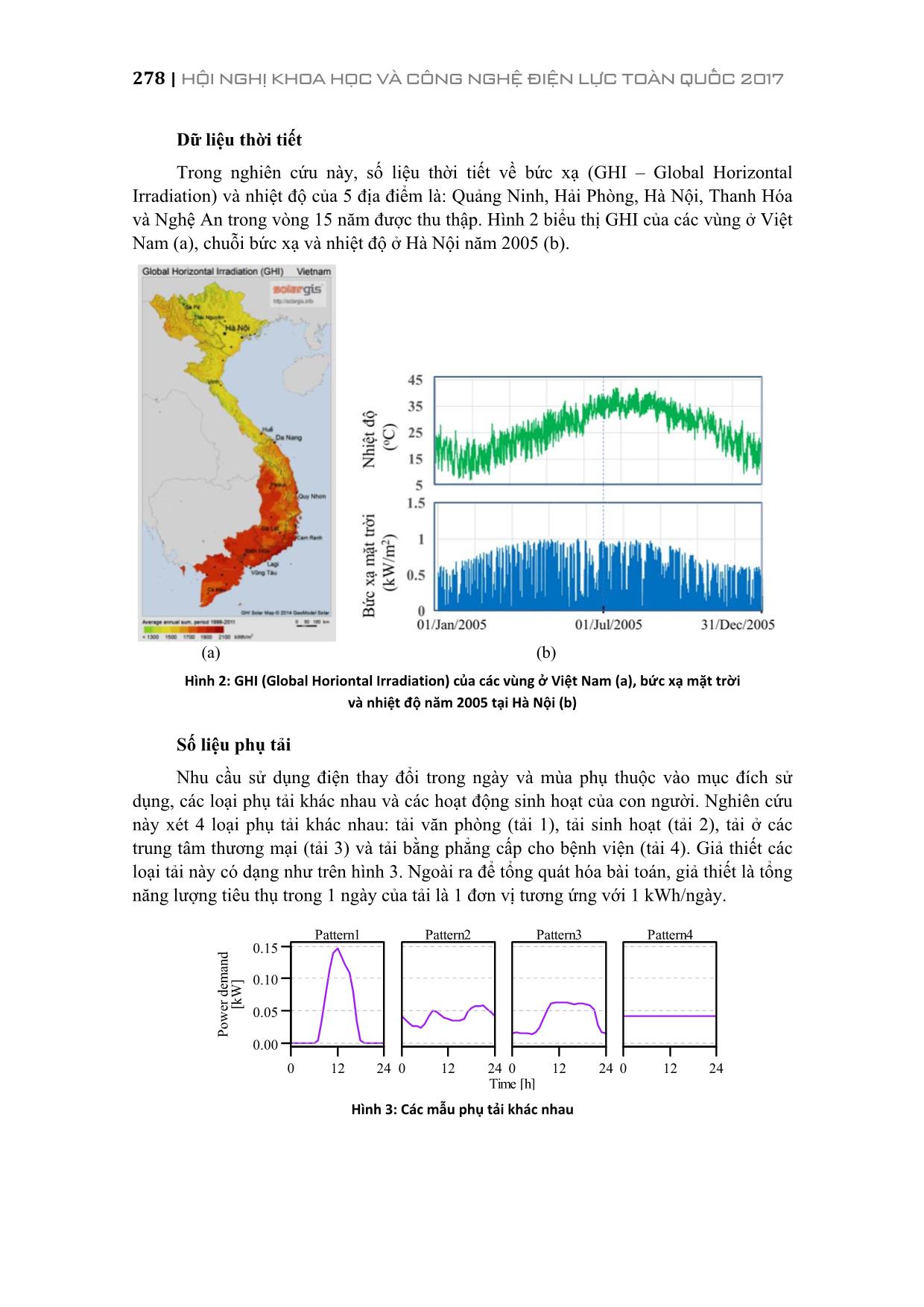
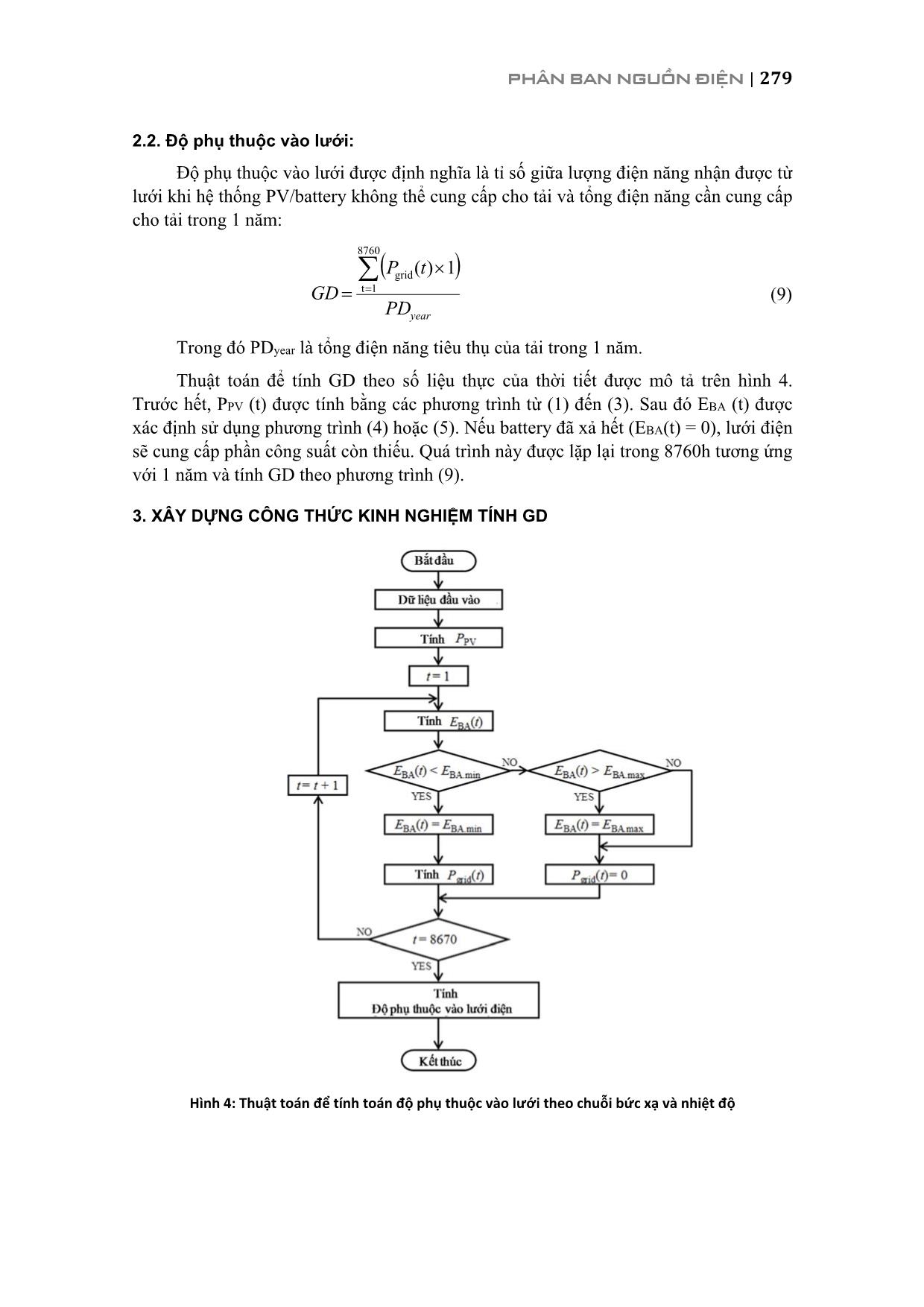
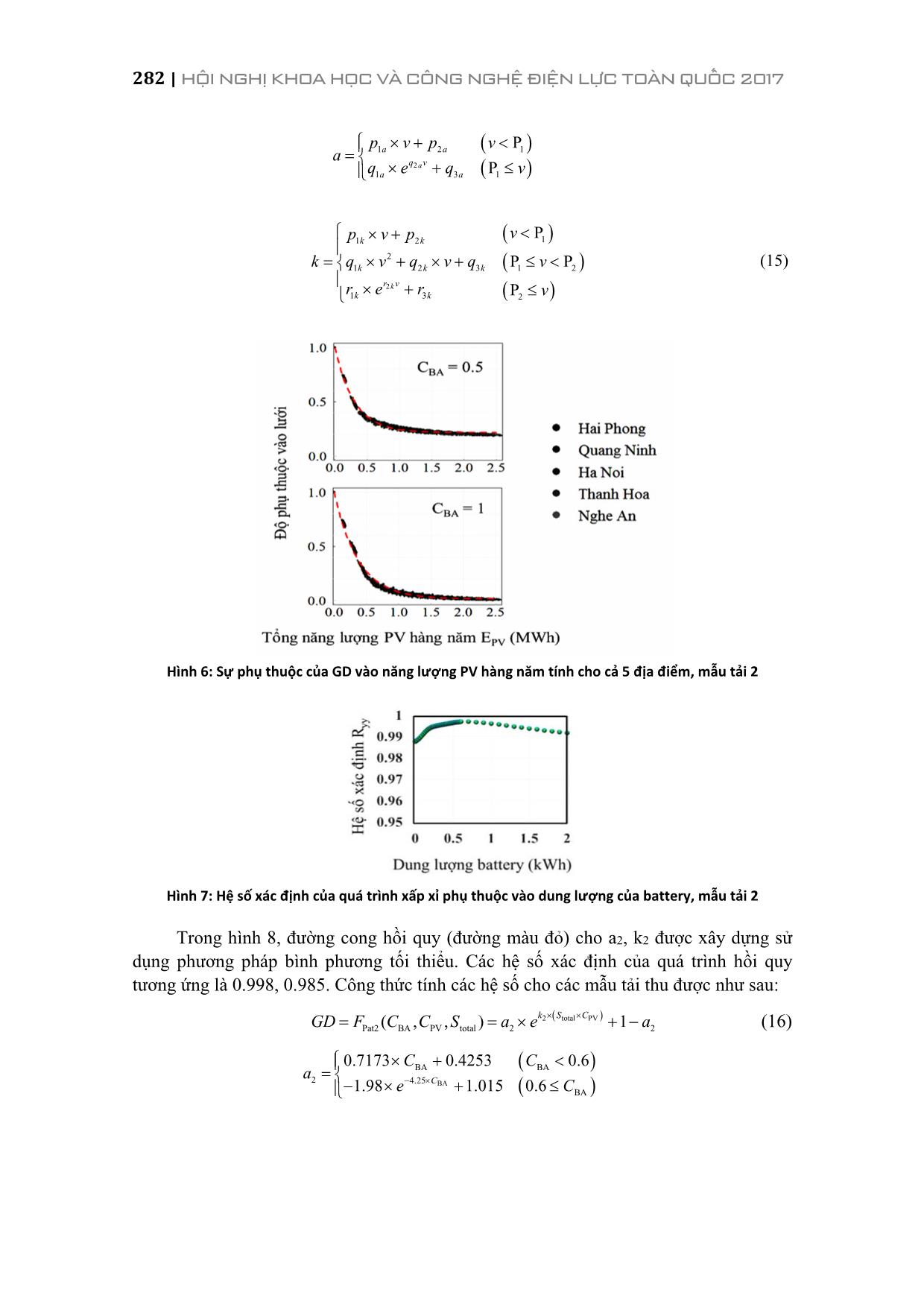
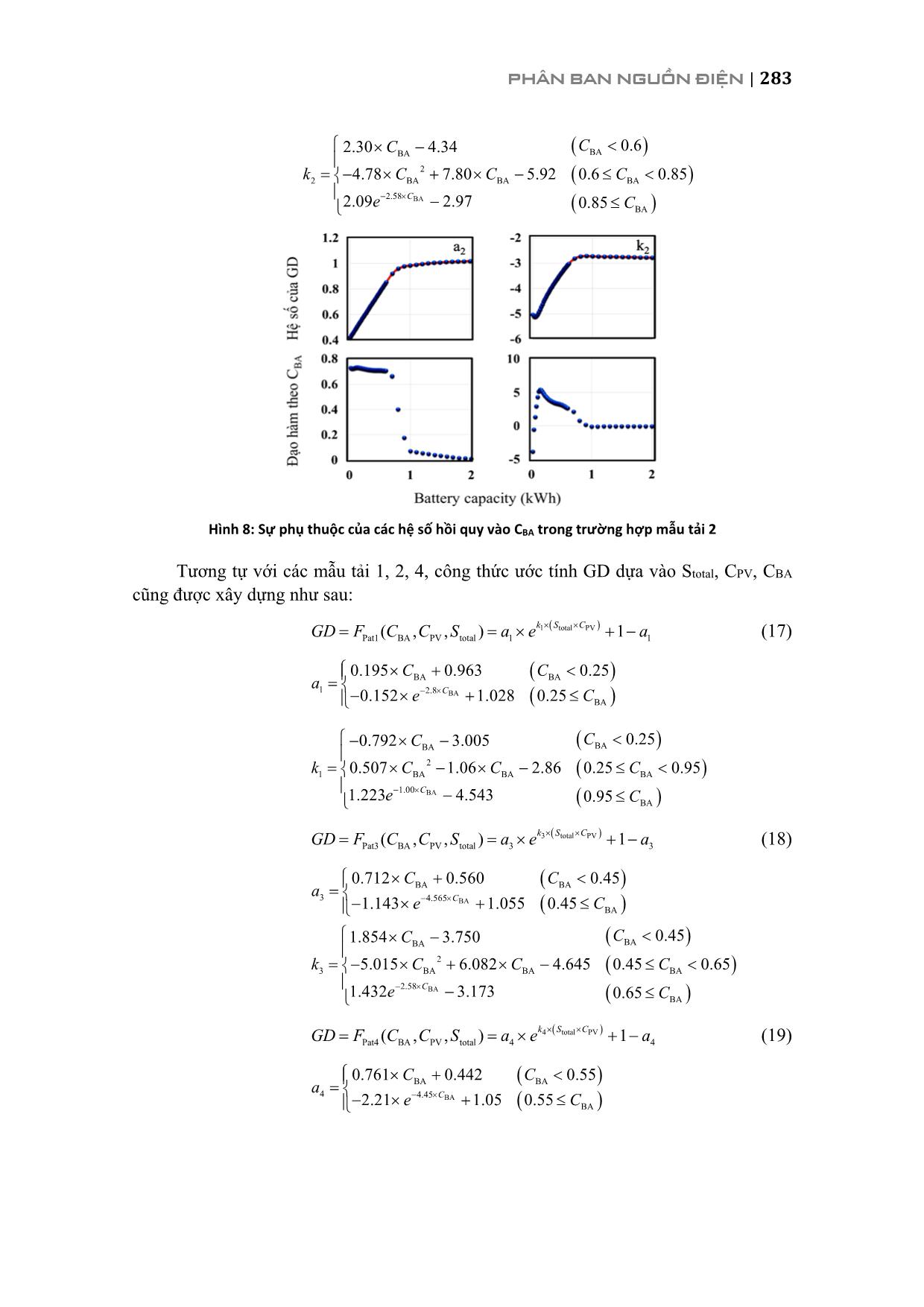
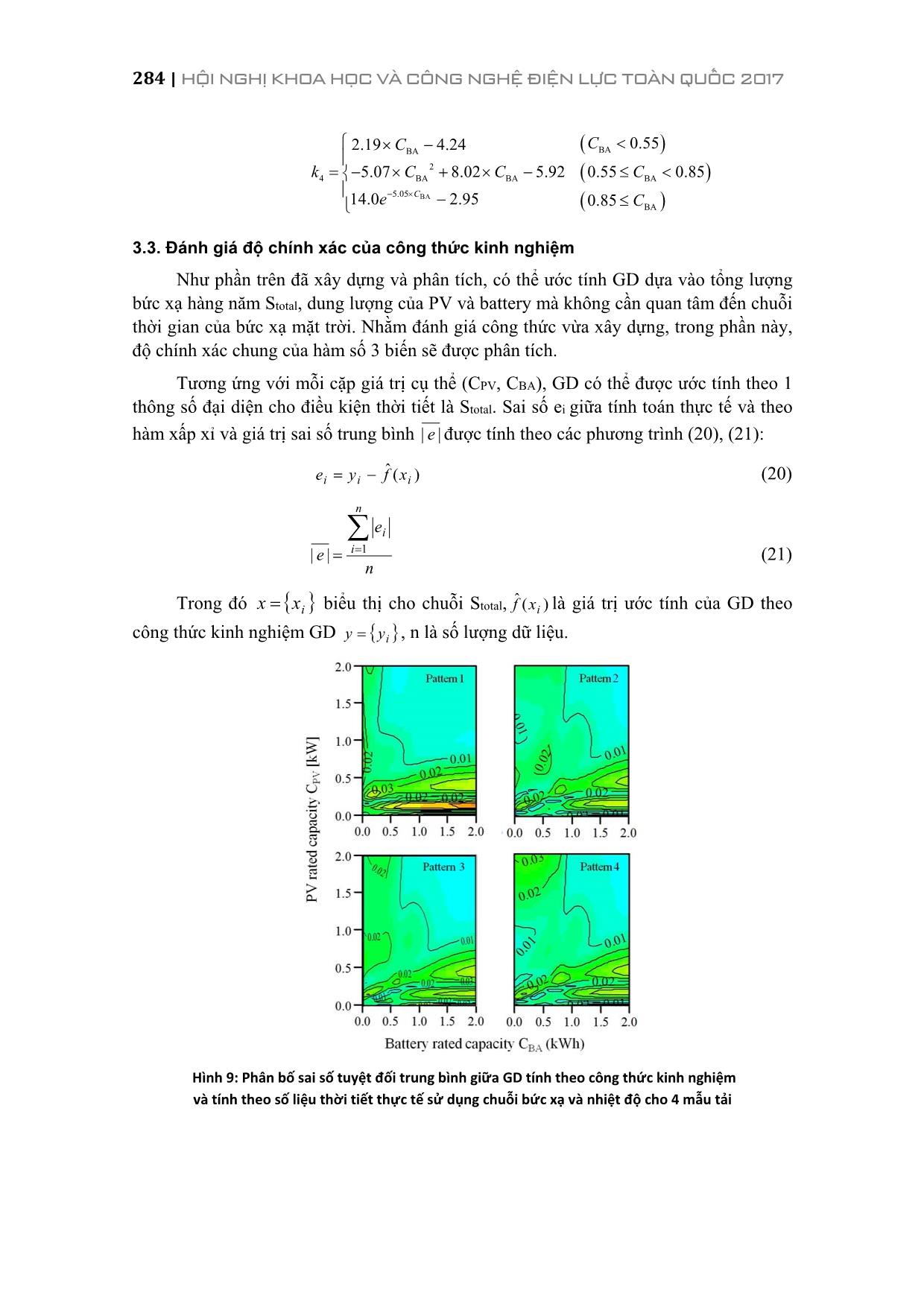
ình 5) 
như sau: 
 step
discharge
BABABA t
1)(1)1()( ηtPσtEtE (4) 
 stepchargeBABABA t)(1)1()( ηtPσtEtE (5) 
Với EBA (t) là lượng điện năng trong battery ở thời điểm t, σ là tốc độ tự xả trong 
1 giờ (4.6 × 10-4 /h) và ηcharge, ηdischarge tương ứng là hiệu suất của quá trình nạp và xả 
(ηcharge = ηdischarge = 0.9). PBA(t) là công suất của battery ở thời điểm t, chính là công suất 
xả hoặc nạp trong các phương trình (6) và (7): 
BA PV CONV
INV
( )( ) ( ) PD tP t P t ηη
 (6) 
BA PV
INV CONV
( ) 1( ) ( )PD tP t P tη η
 (7) 
Trong đó PD(t) là công suất phụ tải ở thời điểm t, ηINV, ηCONV là hiệu suất của bộ 
chuyển đổi (ηINV = ηCONV = 0.9). EBA(t) sẽ bị giới hạn trong phạm vi (0,CBA) (kWh). Khi 
battery đã xả hết, phần công suất thiếu không đủ sẽ được cung cấp từ lưới: 
grid PV
INV
( )( ) ( )PD tP t P tη (8) 
Pgrid(t) (kW) là phần công suất nhận từ lưới tại thời điểm t nếu có. 
278 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
Dữ liệu thời tiết 
Trong nghiên cứu này, số liệu thời tiết về bức xạ (GHI – Global Horizontal 
Irradiation) và nhiệt độ của 5 địa điểm là: Quảng Ninh, Hải Phòng, Hà Nội, Thanh Hóa 
và Nghệ An trong vòng 15 năm được thu thập. Hình 2 biểu thị GHI của các vùng ở Việt 
Nam (a), chuỗi bức xạ và nhiệt độ ở Hà Nội năm 2005 (b). 
 (a) (b) 
Hình 2: GHI (Global Horiontal Irradiation) của các vùng ở Việt Nam (a), bức xạ mặt trời 
và nhiệt độ năm 2005 tại Hà Nội (b) 
Số liệu phụ tải 
Nhu cầu sử dụng điện thay đổi trong ngày và mùa phụ thuộc vào mục đích sử 
dụng, các loại phụ tải khác nhau và các hoạt động sinh hoạt của con người. Nghiên cứu 
này xét 4 loại phụ tải khác nhau: tải văn phòng (tải 1), tải sinh hoạt (tải 2), tải ở các 
trung tâm thương mại (tải 3) và tải bằng phẳng cấp cho bệnh viện (tải 4). Giả thiết các 
loại tải này có dạng như trên hình 3. Ngoài ra để tổng quát hóa bài toán, giả thiết là tổng 
năng lượng tiêu thụ trong 1 ngày của tải là 1 đơn vị tương ứng với 1 kWh/ngày. 
Hình 3: Các mẫu phụ tải khác nhau 
0 12 24
Pattern1
0 12 24
Pattern2
0 12 24
Pattern3
0 12 24
Pattern4
0.00
0.05
0.10
0.15
Po
w
er
 d
em
an
d
[k
W
]
Time [h]
PHÂN BAN NGUỒN ĐIỆN | 279 
2.2. Độ phụ thuộc vào lưới: 
Độ phụ thuộc vào lưới được định nghĩa là tỉ số giữa lượng điện năng nhận được từ 
lưới khi hệ thống PV/battery không thể cung cấp cho tải và tổng điện năng cần cung cấp 
cho tải trong 1 năm: 
yearPD
tP
GD

8760
1t
grid 1)(
 (9) 
Trong đó PDyear là tổng điện năng tiêu thụ của tải trong 1 năm. 
Thuật toán để tính GD theo số liệu thực của thời tiết được mô tả trên hình 4. 
Trước hết, PPV (t) được tính bằng các phương trình từ (1) đến (3). Sau đó EBA (t) được 
xác định sử dụng phương trình (4) hoặc (5). Nếu battery đã xả hết (EBA(t) = 0), lưới điện 
sẽ cung cấp phần công suất còn thiếu. Quá trình này được lặp lại trong 8760h tương ứng 
với 1 năm và tính GD theo phương trình (9). 
3. XÂY DỰNG CÔNG THỨC KINH NGHIỆM TÍNH GD 
Hình 4: Thuật toán để tính toán độ phụ thuộc vào lưới theo chuỗi bức xạ và nhiệt độ 
280 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
Như ở trong phần đặt vấn đề đã đề cập, nghiên cứu này có mục đích là xây dựng 
công thức kinh nghiệm để tính GD phụ thuộc vào thời tiết và dung lượng các thiết bị. 
Trong mục này, mối quan hệ giữa GD và tổng lượng bức xạ hàng năm được phân tích. 
Để xây dựng mối quan hệ này, GD sẽ được tính toán theo thuật toán trong hình 4 dựa 
vào số liệu thực tế của bức xạ mặt trời và nhiệt độ ở 5 địa điểm khác nhau trong vòng 
15 năm. Sau đó, từ kết quả tính toán, sử dụng phương pháp xấp xỉ hồi quy để thành lập 
hàm quan hệ của GD và các thông số. 
3.1. Mối quan hệ của GD vào tổng lượng bức xạ hàng năm 
Với mục đích phân tích mối quan hệ giữa GD và tổng lượng bức xạ hàng năm 
Stotal, nghiên cứu đã sử dụng số liệu thời tiết bao gồm bức xạ và nhiệt độ của 5 địa điểm 
trong vòng 15 năm để tính GD. Dựa trên kết quả tính toán này, mối quan hệ giữa GD và 
Stotal được thiết lập và biểu diễn trên hình 5. Có thể nhận thấy GD tỉ lệ tuyến tính với 
Stotal. Nếu coi Stotal là chuỗi ixx và GD là chuỗi iyy , hệ số tương quan rxy đo độ 
lớn và hướng của mối quan hệ giữa x và y [15] được tính như sau: 
yx
xy
xy ss
s
r (10) 
Với 
n
i
ix xxn
s
1
21 , 
n
i
iy yyn
s
1
21 , 
n
i
iixy yyxxn
s
1
1 (11) 
Trong đó sx, sy tương ứng là độ phân tán của x và y, sxy là hiệp phương sai của x 
và y. x , y là giá trị trung bình của x và y. 
Mức độ tương quan được coi là mạnh nếu giá trị tuyệt đối của rxy càng gần 1. 
Như vậy có thể tính toán GD dựa trên Stotal mà không cần quan tâm đến dạng sóng 
của chuỗi số liệu thời tiết, nghĩa là có thể dùng 1 thông số đại diện cho điều kiện thời 
tiết, đó là tổng lượng bức xạ hàng năm. Chỉ cần biết tổng lượng bức xạ hàng năm là có 
thể ước tính GD nếu biết dung lượng các thiết bị và loại phụ tải. 
Hình 5: Mối quan hệ giữa GD và tổng lượng bức xạ hàng năm Stotal tính với cả 5 địa điểm tương ứng 
với 1 vài giá trị cụ thể dung lượng của PV/battery, mẫu tải 2 
PHÂN BAN NGUỒN ĐIỆN | 281 
3.2. Sự phụ thuộc của GD vào dung lượng PV và battery 
Dựa trên phát hiện về sự phụ thuộc của GD vào Stotal, tác giả đã đề xuất phương 
pháp xác định GD dựa trên Stotal, CPV, CBA mà không cần xét theo năm, khu vực và đặc 
biệt là không cần chuỗi số liệu thời tiết. Nhằm mục đích xây dựng công thức GD là hàm 
của Stotal, CPV, CBA, nghiên cứu sử dụng mô hình hồi quy để tìm mối quan hệ của GD 
với 1 biến, sau đó các hệ số hồi quy sẽ tiếp tục là hàm của các biến còn lại. 
Có thể thấy GD phụ thuộc vào lượng điện PV phát ra hàng năm, là đại lượng được 
xác định bằng tích số của CPV và Stotal như trong biểu thức sau: 
PV total PVE S C (12) 
Do đó, mối quan hệ giữa GD và năng lượng PV hàng năm PVE được phân tích. 
Hình 6 biểu diễn mối quan hệ này trong một số trường hợp CBA khác nhau. Kết quả cho 
thấy các điểm được phân bố theo dạng hàm mũ. Mô hình hồi quy của hàm mũ được lựa 
chọn như sau: 
( ) 1kwig w a e a (13) 
Trong đó iww là năng lượng PV hàng năm PVE . a, k là các hệ số hồi quy. 
Sử dụng phương pháp bình phương tối thiểu, các hệ số này được xác định tương 
ứng với mỗi CBA khác nhau. Hệ số xác định 2yˆyR dùng để đánh giá độ chính xác của hàm 
tìm được, 2yˆyR được tính như sau: 
2
2 1
ˆ
2
1
( )
1
n
i
i
yy n
i
y g w
R
y y


 (14) 
Trong đó iyy là GD, n là số lượng dữ liệu. Hệ số xác định 2yˆyR cho thấy độ phù 
hợp giữa kết quả thực tế với mô hình hàm như thế nào. 2yˆyR càng gần 1 thì hàm số tìm 
được càng chính xác. Hình 7 biểu diễn hệ số xác định 2yˆyR tương ứng với CBA. Giá trị 
nhỏ nhất của 2yˆyR là 0.987 trong khi giá trị lớn nhất là gần bằng 1. 2yˆyR cao chứng tỏ lựa 
chọn hàm số dạng mũ là hợp lý và các hệ số tìm được tương đối chính xác. 
Tương tự, mô hình hàm mũ cũng được áp dụng để xấp xỉ mối quan hệ giữa GD và 
PVE trong trường hợp mẫu tải 1, 3 và 4. 
Các hệ số hồi quy a và k được coi là hàm của CBA. Hình 8 biểu diễn sự phụ thuộc 
của các hệ số này vào CBA trong trường hợp mẫu tải 2. Dựa vào đạo hàm, hàm số của 
các hệ số này với CBA được rút ra theo phương trình hồi quy sau: 
282 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
 21 2 11 3 1
P
Pa
a a
q v
a a
p v p v
a
q e q v
 2
11 2
2
1 2 3 1 2
1 3 2
P
P P
Pk
k k
k k k
r v
k k
vp v p
k q v q v q v
r e r v
 (15) 
Hình 6: Sự phụ thuộc của GD vào năng lượng PV hàng năm tính cho cả 5 địa điểm, mẫu tải 2 
Hình 7: Hệ số xác định của quá trình xấp xỉ phụ thuộc vào dung lượng của battery, mẫu tải 2 
Trong hình 8, đường cong hồi quy (đường màu đỏ) cho a2, k2 được xây dựng sử 
dụng phương pháp bình phương tối thiểu. Các hệ số xác định của quá trình hồi quy 
tương ứng là 0.998, 0.985. Công thức tính các hệ số cho các mẫu tải thu được như sau: 
 2 total PV
Pat2 BA PV total 2 2( , , ) 1
k S CGD F C C S a e a (16) 
 BABA BA2 4.25 BA
0.7173 0.4253 0.6
1.98 1.015 0.6C
C C
a
e C 
PHÂN BAN NGUỒN ĐIỆN | 283 
 BA
BABA
2
2 BA BA BA
2.58
BA
0.62.30 4.34
4.78 7.80 5.92 0.6 0.85
2.09 2.97 0.85C
CC
k C C C
e C 
Hình 8: Sự phụ thuộc của các hệ số hồi quy vào CBA trong trường hợp mẫu tải 2 
Tương tự với các mẫu tải 1, 2, 4, công thức ước tính GD dựa vào Stotal, CPV, CBA 
cũng được xây dựng như sau: 
 1 total PV
Pat1 BA PV total 1 1( , , ) 1
k S CGD F C C S a e a (17) 
 BABA BA1 2.8 BA
0.195 0.963 0.25
0.152 1.028 0.25C
C C
a
e C 
 BA
BABA
2
1 BA BA BA
1.00
BA
0.250.792 3.005
0.507 1.06 2.86 0.25 0.95
1.223 4.543 0.95C
CC
k C C C
e C 
 3 total PV
Pat3 BA PV total 3 3( , , ) 1
k S CGD F C C S a e a (18) 
 BABA BA3 4.565 BA
0.712 0.560 0.45
1.143 1.055 0.45C
C C
a
e C 
 BA
BABA
2
3 BA BA BA
2.58
BA
0.451.854 3.750
5.015 6.082 4.645 0.45 0.65
1.432 3.173 0.65C
CC
k C C C
e C 
 4 total PV
Pat4 BA PV total 4 4( , , ) 1
k S CGD F C C S a e a (19) 
 BABA BA4 4.45 BA
0.761 0.442 0.55
2.21 1.05 0.55C
C C
a
e C 
284 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
 BA
BABA
2
4 BA BA BA
5.05
BA
0.552.19 4.24
5.07 8.02 5.92 0.55 0.85
14.0 2.95 0.85C
CC
k C C C
e C 
3.3. Đánh giá độ chính xác của công thức kinh nghiệm 
Như phần trên đã xây dựng và phân tích, có thể ước tính GD dựa vào tổng lượng 
bức xạ hàng năm Stotal, dung lượng của PV và battery mà không cần quan tâm đến chuỗi 
thời gian của bức xạ mặt trời. Nhằm đánh giá công thức vừa xây dựng, trong phần này, 
độ chính xác chung của hàm số 3 biến sẽ được phân tích. 
Tương ứng với mỗi cặp giá trị cụ thể (CPV, CBA), GD có thể được ước tính theo 1 
thông số đại diện cho điều kiện thời tiết là Stotal. Sai số ei giữa tính toán thực tế và theo 
hàm xấp xỉ và giá trị sai số trung bình || e được tính theo các phương trình (20), (21): 
 )(ˆ iii xfye (20) 
n
e
e
n
i
i
 1|| (21) 
Trong đó ixx biểu thị cho chuỗi Stotal, )(ˆ ixf là giá trị ước tính của GD theo 
công thức kinh nghiệm GD iyy , n là số lượng dữ liệu. 
 Hình 9: Phân bố sai số tuyệt đối trung bình giữa GD tính theo công thức kinh nghiệm 
và tính theo số liệu thời tiết thực tế sử dụng chuỗi bức xạ và nhiệt độ cho 4 mẫu tải 
PHÂN BAN NGUỒN ĐIỆN | 285 
Sử dụng CPV trong khoảng từ 0 kW đến 2 kW với bước 0.05 kW, CBA từ 0 đến 2 
kWh với bước 0.05 kWh, sai số tuyệt đối trung bình tương ứng với mỗi cặp (CPV, CBA) 
được tính và biểu diễn trên hình 10 cho mẫu tải 2. Màu sắc càng chuyển sang màu vàng 
đỏ thì || e càng lớn và ngược lại, càng chuyển sang màu xanh thì || e càng nhỏ. Từ hình 
10, có thể thấy || e tương đối nhỏ trong vùng CPV và CBA cao. Trong khi đó, giá trị lớn 
nhất của || e là 0.05, trong vùng CPV = 0.5 kW. Để tăng độ chính xác, có thể tăng số biến 
phụ thuộc, chẳng hạn xét cả địa điểm trong công thức GD hoặc sử dụng mô hình hồi 
quy phức tạp hơn để xấp xỉ. 
Sai số tuyệt đối trung bình được tính tương tự cho các mẫu tải 1, 3 và 4 và biểu 
diễn trên hình 9. Nhìn chung, chúng tương đối nhỏ và có thể nói rằng công thức GD đã 
xây dựng có độ chính xác cao. 
4. KẾT LUẬN 
Trong bài báo này, công thức kinh nghiệm để ước tính độ phụ thuộc vào lưới của 
hệ thống PV/battery cấp điện cho các loại phụ tải khác nhau đã được xây dựng. Từ kết 
quả tính toán GD dựa trên số liệu thời tiết thực tế tại 5 vùng, có thể rút ra kết luận là GD 
phụ thuộc vào tổng lượng bức xạ hàng năm, dung lượng của PV và battery. Mô hình 
xấp xỉ hồi quy được sử dụng để tìm ra mối quan hệ giữa GD và các đại lượng này. Kết 
quả cho thấy hàm tìm được có độ chính xác cao và có thể áp dụng để ước tính một cách 
đơn giản độ phụ thuộc của hệ thống này vào lưới. 
Lời cảm ơn 
Nghiên cứu này được tài trợ bởi Trường Đại học Bách khoa Hà Nội theo chương 
trình đề tài phân cấp PC 2017. 
TÀI LIỆU THAM KHẢO 
[1] M. Iqbalb, M. Azam, M. Naeem, A.S. Khwaja, A. Anpalagan, Optimization classification, 
algorithms và tools for renewable energy: A review, Renewable và Sustainable Energy 
Reviews 39 (2014) 640–654. 
[2] Prabodh Bajpai, Vaishalee Dash, Hybrid renewable energy systems for power 
generation in stand-alone applications: A review, Renewable và Sustainable Energy 
Reviews 16 (2012) 2926–2939. 
[3] T.T.H. Nguyen, T. Nakayama, M. Ishida, Power Control Method Using Kalman Filter 
Prediction for Stable Operation of PV/FC/LiB Hybrid Power System Based on 
Experimental Dynamic Characteristics, Journal of the Japan Institute of Energy, 94 
(2015) 532-541. 
[4] A.R.De, L. Musgrove, The optimization of hybrid energy conversion systems using the 
dynamic programming model - Rapsody, International Journal of Energy Research 
12(1988) 447-457. 
286 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
[5] Yang HX, Lu L, Zhou W. A novel optimization sizing model for hybrid solar – wind 
power generation system, Solar Energy, 81(1) (2007) 76-84. 
[6] Borowy BS, Salameh ZM, Methodology for optimally sizing the combination of a 
battery bank và PV array in a wind/PV hybrid system. IEEE Transactions on Energy 
Conversion 11(2) (1996) 367-373. 
[7] Diaf, D. Diaf, M. Belhamel, M. Haddadi, A. Louche, A methodology for optimal sizing of 
autonomous hybrid PV/wind system, Energy Policy 35 (2007) 5708–5718. 
[8] Diaf, G. Notton, M. Belhamel, M. Haddadi, A. Louche, Design and techno–economical 
optimization for hybrid PV/wind system under various meteorological conditions, 
Applied Energy 85 (2008) 968–987. 
[9] Hongxing Yang, Lin Lu, Wei Zhou, A novel optimization sizing model for hybrid solar-
wind power generation system, Solar Energy 81 (2007) 76–84. 
[10] Zachariah Iverson, Ajit Achuthan, Pier Marzocca, Daryush Aidun, Optimal design of 
hybrid renewable energy systems (HRES) using hydrogen storage technology for data 
center applications, Renewable Energy 52 (2013) 79–87. 
[11] H.X. Yang, L. Lu, J. Burnett, Weather data and probability analysis of hybrid 
photovoltaic-wind power generation systems in Hong Kong, Renewable Energy 28 
(2003) 1813–1824. 
[12] A. Kashefi Kaviani, G.H. Riahy, SH.M. Kouhsari, Optimal design of a reliable hydrogen-
based stand-alone wind/PV generating system, considering component outages, 
Renewable Energy 34 (2009) 2380–2390. 
[13] N.Z. Al-Rawahi, Y.H. Zurigat and N.A. Al-Azri, Prediction of Hourly Solar Radiation on 
Horizontal and Inclined Surfaces for Muscat/Oman, The Journal of Engineering 
Research 8 (2) (2011) 19–31. 
[14] Robert Foster, Majid Ghassemi, Alma Cota, (2010), Solar Energy: Renewable Energy 
and the Environment, CRC Press, Taylor & Francis Group. 
[15] Rui Xiong, Xianzhi Gong, Chunting Chris Mi, Fengchun Sun, A robust state–of–charge 
estimator for multiple types of lithium-ion batteries using adaptive extended Kalman 
Filter, Journal of Power Sources 243 (2013) 805-816 
[16] T.H.T. Nguyen, T. Nakayama, M. Ishida, Optimal capacity design of battery and 
hydrogen system for the DC grid with photovoltaic power generation based on the 
rapid estimation of grid dependency, International Journal of Electrical Power and 
Energy Systems, 89 (2017) 27-39