Ứng dụng chiến lược vét cạn để tối ưu cân bằng dây chuyền may công nghiệp

ghệ không thể hiện được. Các NCCN có thể thay đổi 
thứ tự cho nhau được biểu diễn ở 2 nhánh song song. 
Ví dụ NCCN số 24 và số 25 có thể thay đổi thứ tự thực 
hiện cho nhau, NCCN số 27 và 28 có thể đổi thứ tự 
thực hiện cho nhau mà không ảnh hưởng đến hành 
trình công nghệ. Khi chuyển sang sơ đồ ưu tiên công 
nghệ đỉnh 24 và 25, đỉnh 27 và 28 được biểu diễn ở 2 
nhánh song song trong sơ đồ ưu tiên công nghệ hình 3, 
mô hình này được giải thích như sau NCCN 23 thực 
hiện xong sẽ chuyển sang NCCN 24 hoặc 25, sau khi 
thực hiện xong NCCN 24 và 25 thì mới chuyển sang 
NCCN 26, tương tự NCCN 26 thực hiện xong sẽ 
chuyển sang NCCN 27 hoặc 28, sau khi thực hiện xong 
NCCN 27 và 28 thì mới chuyển sang NCCN 29. 
2.2.3. Tính toán các thông số của dây chuyền 
Gọi tsxj là thời gian của NCSX j, ta có: 
𝑡𝑡𝑠𝑠𝑠𝑠𝑠𝑠 = ∑ 𝑡𝑡𝑠𝑠𝑖𝑖𝑚𝑚𝑖𝑖𝑖𝑖=1 (𝑠𝑠) (4) 
Số công nhân tính toán của mỗi NCSXj là Ntj: 
𝑁𝑁𝑡𝑡𝑠𝑠 = 𝑡𝑡𝑠𝑠𝑠𝑠𝑠𝑠𝑅𝑅 (5) 
Gọi Ncj là số công nhân chọn theo nguyên tắc làm 
tròn, nhịp riêng của mỗi NCSX thứ j là Rj, được xác định 
như sau: 
𝑅𝑅𝑠𝑠 = 𝑡𝑡𝑠𝑠𝑠𝑠𝑠𝑠𝑁𝑁𝑙𝑙𝑠𝑠 (𝑠𝑠) (6) 
Gọi k là số NCSX được tạo thành thì tổng số công 
nhân sản xuất (Nsx) là: 
𝑁𝑁𝑠𝑠𝑠𝑠 = ∑ 𝑁𝑁𝑐𝑐𝑠𝑠𝑘𝑘𝑖𝑖=1 (𝑛𝑛𝑛𝑛ườ𝑖𝑖) (7) 
Gọi số NCSX thỏa mãn điều kiện Rmin ≤ Rj ≤ Rmax 
là k1, tỷ lệ NCSX thỏa mãn điều kiện nhịp H1 được xác 
định theo công thức sau: 
𝐻𝐻1 = 𝑘𝑘1𝑘𝑘 100 (%) (8) 
2.2.4. Phương pháp phối hợp các nguyên công công 
nghệ thành nguyên công sản xuất. 
Phối hợp các NCCN thành NCSX phải đảm bảo 
tính trình tự công nghệ để đường đi của bán thành 
phẩm là thẳng dòng và ngắn nhất. Có thể ghép các đỉnh 
của cùng một nhánh gia công, ví dụ ghép NCCN số 1 
với 2, là các nguyên công nằm trên cùng nhánh, có 
đường đi từ 1 đến 2. Có thể theo nguyên tắc song song 
tức là ghép các đỉnh trên các nhánh khác nhau nhưng 
không ảnh hưởng đến tính trình tự công nghệ, ví dụ 
ghép NCCN số 1 với 8 là 2 NCCN khác nhánh. 
Bán thành phẩm không được vận chuyển qua lại 
giữa các NCSX, ví dụ trong hình 4 minh họa NCSX1 
gồm NCCN số 1, 2, 5 và 6, NCSX2 gồm NCCN số 3 và 
7. Đường đi của các nguyên công theo sơ đồ ưu tiên 
hình 3 là 1→2→3→6→7, trường hợp này đường đi 
của vật liệu di chuyển qua lại giữa NCSX1 và NCSX2, 
do vậy không đảm bảo tính trình tự công nghệ. 
Hình 3. Sơ đồ ưu tiên công nghệ 
Hình 4. Đường đi của bán thành phẩm di chuyển qua 
lại giữa các NCSX. 
1
2
3
5
6
7
18
19
20
21
22
23
26
27 28
30
29
24 25
8
9
10
11
12
13
14
15
16
17
4
Tạp chí Khoa học và Công nghệ 141 (2020) 034-041 
38 
2.2.5. Lựa chọn thuật toán tối ưu cân bằng chuyền 
Vét cạn là chiến lược thiết kế giải thuật, là 
phương pháp tìm nghiệm của bài toán tối ưu bằng cách 
xem xét tất cả các phương án có thể để tìm ra nghiệm 
tốt nhất. Ưu điểm lớn nhất của phương pháp vét cạn là 
luôn tìm ra nghiệm chính xác. Đối với bài toán cân 
bằng chuyền may sản phẩm áo Polo-Shirt, số lượng các 
đỉnh là 30 không quá lớn, sơ đồ ưu tiên là một dạng đồ 
thị có hướng, không có chu trình, vì vậy, có thể áp dụng 
phương pháp vét cạn để giải bài toán này. 
3. Kết quả nghiên cứu 
3.1. Thuật toán tối ưu cân bằng chuyền 
Bài toán cân bằng dây chuyền may trong nghiên 
cứu này được xây dựng với mục tiêu tối thiểu số lượng 
công nhân tham gia sản xuất trên dây chuyền. 
Dữ liệu đầu vào gồm: Trình tự công nghệ của các 
NCSX được tham số hóa bằng danh sách cạnh [9], thời 
gian, tên máy, loại máy của các NCCN. Bằng thuật 
toán áp dụng chiến lược vét cạn với các điều kiện ràng 
buộc, kết quả thu được là bảng NCSX và các chỉ số hiệu 
quả dây chuyền, tỷ lệ phần trăm NCSX thỏa mãn điều 
kiện nhịp. Thuật toán cân bằng chyền áp dụng chiến 
lược vét cạn như sau: 
Giả thiết Tập NCSX cần tìm có dạng (NCSX1, 
NCSX2,  NCSXk), áp dụng chiến lược vét cạn thiết kế 
giải thuật được mô tả như sau: 
Bước 1. Xét tất cả các NCCN mà NCSX1 có thể nhận 
được, thử cho NCSX1 nhận lần lượt các NCCN đó. Với 
mỗi NCCN thử cho NCSX1 tiến hành kiểm tra: 
- Nếu NCSX1 thỏa mãn điều kiện nhịp thì chuyển 
NCSX1 vào Tập NCSX. 
- Nếu NCSX1 không thỏa mãn điều kiện nhịp, xét 
tiếp các NCCN còn lại thỏa mãn điều kiện trình tự và 
thiết bị để ghép với NCCN đã có trong NCSX1, thử cho 
NCSX1 nhận lần lượt các NCCN đó. Với mỗi bước thử 
lại tiến hành kiểm tra điều kiện nhịp, nếu không tìm 
được thì chuyển NCSX1 vào Tập NCSX. 
Với mỗi kết quả tìm được NCSX1 ta sẽ thực hiện: 
Bước 2. Xét tất cả các NCCN mà NCSX2 có thể nhận 
được, thử cho NCSX2 nhận lần lượt các giá trị đó. Với 
mỗi NCCN thử cho NCSX2 tiến hành kiểm tra như 
bước 1. 
Tiếp tục như vậy đến bước k: 
Bước k. Giả sử tất cả các NCCN từ 1 cho đến k-1 đã 
được xếp vào Tập NCSX, tiếp tục xét đến NCCN thứ 
k (Try(k)). Có hai trường hợp xảy ra:. 
Trường hợp 1: NCCN thứ k đã được xếp vào cùng 
nhóm với các NCCN trước đó. 
Trường hợp 2: NCCN thứ k chưa được xếp vào 
nhóm nào. 
Tiến hành xử lí từng trường hợp như sau: 
- Trường hợp 1: NCCN thứ k đã được xếp. 
Nếu k = n, nghĩa là mọi NCCN đã được xếp 
thì chuyển Tập NCSX này đến một hàm Xuat(), hàm 
này xét xem Tập NCSX có số công nhân nhỏ hơn Tập 
NCSX trước đó không, nếu có số công nhân nhỏ hơn 
thì sẽ xuất còn không thì bỏ qua. 
Nếu k < n, vì NCCNk đã được xếp, công việc 
tiếp theo sẽ xét đến NCCN thứ k + 1. 
- Trường hợp 2: NCCN thứ k chưa được xếp. 
Nếu k = n, nghĩa là mọi NCCN trước đó đã 
được xếp, cho NCCN này trở thành một NCSX rồi 
chuyển vào Tập NCSX. 
Nếu k < n, sẽ lập ra một NCSX mới chứa 
NCCNk, khi đó phải tìm các NCCN khác có thể ghép 
được với NCCNk. Quá trình tìm kiếm kết thúc khi 
thành Tập NCSX hoàn chỉnh. Bảng mã giả tối ưu cân 
bằng chuyền được minh họa trong bảng 2. 
Bảng 2. Bảng mã giả tối ưu cân bằng chuyền 
Khởi tạo Tập NCSX để chứa các NCSX. 
Try( k ){ 
If Nếu NCCN k chưa được thêm vào NCSX 
then 
 Tạo một NCSX mới chứa NCCN k; 
 Đánh dấu đã thêm k; 
 if k == n then 
 Thêm NCCN vào NCSX; 
 Xuất; 
 else 
 // Kết hợp các NCCN khác với 
NCCN thứ k để tạo thành một NCSX 
 // Xét các NCCN khác từ k+1 đến n 
 for i1, i2, .. ∈ k + 1 .. n then 
 if Nếu NCCN thứ i chưa 
được thêm vào NCSX, đồng thời thỏa mãn các 
điều kiện về thiết bị, trình tự và thời gian không 
vượt quá 3.3R then 
 Thêm các NCCN thỏa mãn vào 
NCSX; 
 Thêm NCSX vào Tập NCSX; 
 Try (k+1); 
 Bỏ NCSX ra khỏi Tập NCSX; 
 Đánh dấu k tự do; 
else // k đã được thêm vào một NCSX trước đó 
trong Tập NCSX. 
 if k == n then 
 Xuất; 
 else Try(k+1); 
} 
Tạp chí Khoa học và Công nghệ 141 (2020) 034-041 
39 
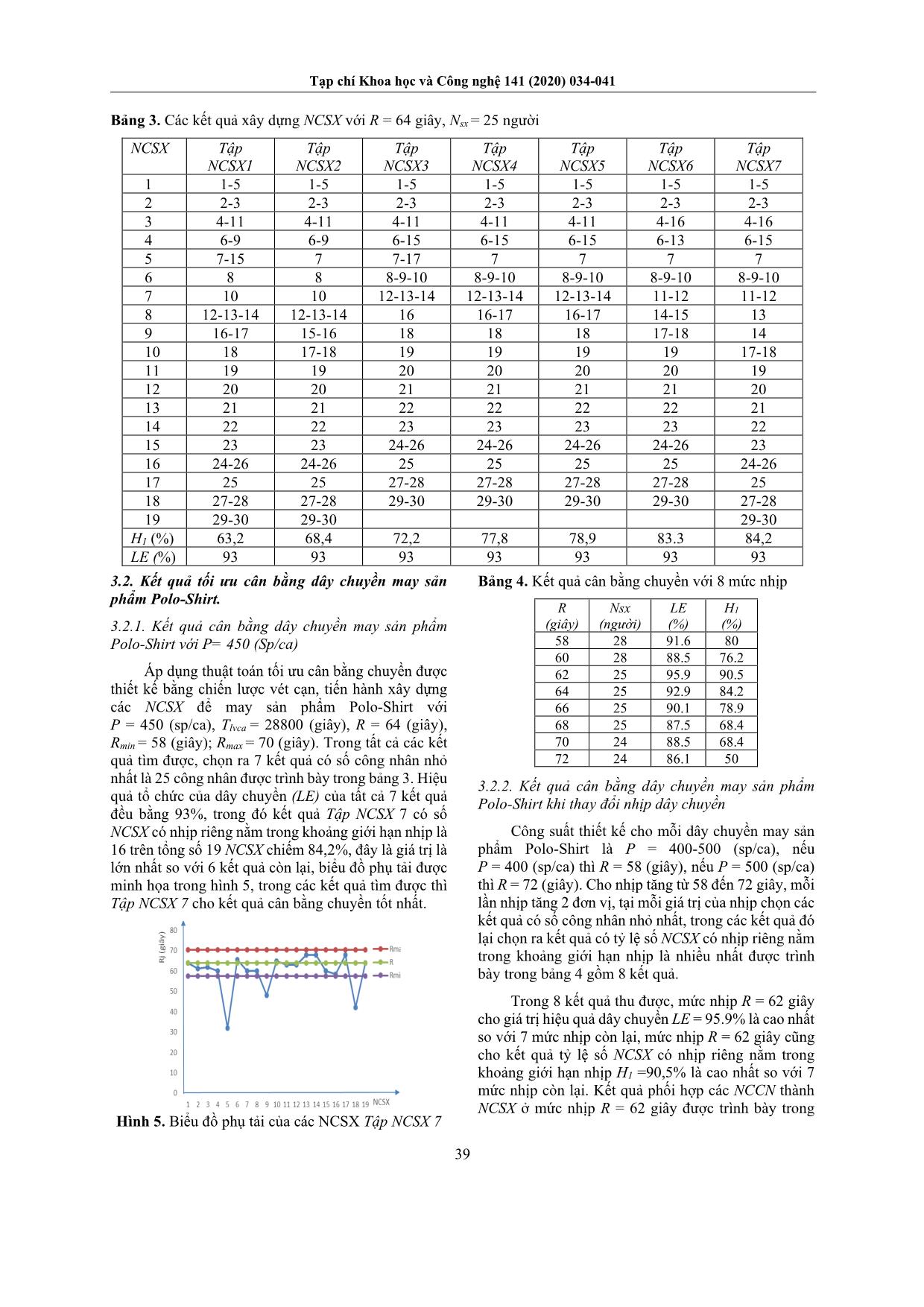
Bảng 3. Các kết quả xây dựng NCSX với R = 64 giây, Nsx = 25 người 
NCSX Tập 
NCSX1 
Tập 
NCSX2 
Tập 
NCSX3 
Tập 
NCSX4 
Tập 
NCSX5 
Tập 
NCSX6 
Tập 
NCSX7 
1 1-5 1-5 1-5 1-5 1-5 1-5 1-5 
2 2-3 2-3 2-3 2-3 2-3 2-3 2-3 
3 4-11 4-11 4-11 4-11 4-11 4-16 4-16 
4 6-9 6-9 6-15 6-15 6-15 6-13 6-15 
5 7-15 7 7-17 7 7 7 7 
6 8 8 8-9-10 8-9-10 8-9-10 8-9-10 8-9-10 
7 10 10 12-13-14 12-13-14 12-13-14 11-12 11-12 
8 12-13-14 12-13-14 16 16-17 16-17 14-15 13 
9 16-17 15-16 18 18 18 17-18 14 
10 18 17-18 19 19 19 19 17-18 
11 19 19 20 20 20 20 19 
12 20 20 21 21 21 21 20 
13 21 21 22 22 22 22 21 
14 22 22 23 23 23 23 22 
15 23 23 24-26 24-26 24-26 24-26 23 
16 24-26 24-26 25 25 25 25 24-26 
17 25 25 27-28 27-28 27-28 27-28 25 
18 27-28 27-28 29-30 29-30 29-30 29-30 27-28 
19 29-30 29-30 29-30 
H1 (%) 63,2 68,4 72,2 77,8 78,9 83.3 84,2 
LE (%) 93 93 93 93 93 93 93 
3.2. Kết quả tối ưu cân bằng dây chuyền may sản 
phẩm Polo-Shirt. 
3.2.1. Kết quả cân bằng dây chuyền may sản phẩm 
Polo-Shirt với P= 450 (Sp/ca) 
Áp dụng thuật toán tối ưu cân bằng chuyền được 
thiết kế bằng chiến lược vét cạn, tiến hành xây dựng 
các NCSX để may sản phẩm Polo-Shirt với 
P = 450 (sp/ca), Tlvca = 28800 (giây), R = 64 (giây), 
Rmin = 58 (giây); Rmax = 70 (giây). Trong tất cả các kết 
quả tìm được, chọn ra 7 kết quả có số công nhân nhỏ 
nhất là 25 công nhân được trình bày trong bảng 3. Hiệu 
quả tổ chức của dây chuyền (LE) của tất cả 7 kết quả 
đều bằng 93%, trong đó kết quả Tập NCSX 7 có số 
NCSX có nhịp riêng nằm trong khoảng giới hạn nhịp là 
16 trên tổng số 19 NCSX chiếm 84,2%, đây là giá trị là 
lớn nhất so với 6 kết quả còn lại, biểu đồ phụ tải được 
minh họa trong hình 5, trong các kết quả tìm được thì 
Tập NCSX 7 cho kết quả cân bằng chuyền tốt nhất. 
Hình 5. Biểu đồ phụ tải của các NCSX Tập NCSX 7 
Bảng 4. Kết quả cân bằng chuyền với 8 mức nhịp 
R 
(giây) 
Nsx 
(người) 
LE 
(%) 
H1 
(%) 
58 28 91.6 80 
60 28 88.5 76.2 
62 25 95.9 90.5 
64 25 92.9 84.2 
66 25 90.1 78.9 
68 25 87.5 68.4 
70 24 88.5 68.4 
72 24 86.1 50 
3.2.2. Kết quả cân bằng dây chuyền may sản phẩm 
Polo-Shirt khi thay đổi nhịp dây chuyền 
Công suất thiết kế cho mỗi dây chuyền may sản 
phẩm Polo-Shirt là P = 400-500 (sp/ca), nếu 
P = 400 (sp/ca) thì R = 58 (giây), nếu P = 500 (sp/ca) 
thì R = 72 (giây). Cho nhịp tăng từ 58 đến 72 giây, mỗi 
lần nhịp tăng 2 đơn vị, tại mỗi giá trị của nhịp chọn các 
kết quả có số công nhân nhỏ nhất, trong các kết quả đó 
lại chọn ra kết quả có tỷ lệ số NCSX có nhịp riêng nằm 
trong khoảng giới hạn nhịp là nhiều nhất được trình 
bày trong bảng 4 gồm 8 kết quả. 
Trong 8 kết quả thu được, mức nhịp R = 62 giây 
cho giá trị hiệu quả dây chuyền LE = 95.9% là cao nhất 
so với 7 mức nhịp còn lại, mức nhịp R = 62 giây cũng 
cho kết quả tỷ lệ số NCSX có nhịp riêng nằm trong 
khoảng giới hạn nhịp H1 =90,5% là cao nhất so với 7 
mức nhịp còn lại. Kết quả phối hợp các NCCN thành 
NCSX ở mức nhịp R = 62 giây được trình bày trong 
Tạp chí Khoa học và Công nghệ 141 (2020) 034-041 
40 
bảng 5, mỗi NCSX chỉ gồm 1 đến 2 NCCN, cần 1 đến 
2 công nhân, các NCSX này đảm bảo điều kiện ràng 
buộc về thiết bị. Số NCSX có nhịp riêng nằm trong 
khoảng giới hạn nhịp 56 ÷ 68 (giây) là 19 NCSX trên 
tổng số 21 NCSX, biểu đồ phụ tải được minh họa trong 
hình 6. Như vậy ở mức nhịp R = 62 giây, xây dựng 
được Tập NCSX có hiệu quả dây chuyền và tỷ lệ NCSX 
nằm trong khoảng dao động nhịp là cao nhất so với các 
mức nhịp còn lại. 
Hình 6. Biểu đồ phụ tải của các NCSX với R = 62 
(giây), Nsx = 25 (người). 
Bảng 5. Kết quả xây dựng NCSX với R = 62 giây 
NCSX Tập 
NCSX 
Thiết bị tsxj 
(giây) 
Ncj 
(người) 
Rj 
(giây) 
1 1-5 MC2K 64 1 64 
2 2 MB1K 56 1 56 
3 3 MB1K 128 2 56 
4 4-16 MB1K 62 1 62 
5 6-9 MX2K 56 1 56 
6 7 MC1K 32 1 32 
7 8 MB1K 56 1 56 
8 10 MB1K 56 1 56 
9 11-12 MB1K 60 1 60 
10 13 BL 60 1 60 
11 14-15 MB1K 119 2 60 
12 17-18 MB1K 65 1 65 
13 19 MX2K 63 1 63 
14 20 MB1K 63 1 63 
15 21 MX2K 68 1 68 
16 22 MC1K 68 1 68 
17 23 MX2K 120 2 60 
18 24-26 MB1K 117 2 59 
19 25 MC2K 68 1 68 
20 27-28 MDB 42 1 42 
21 29-30 
MTK 
MDC 64 1 64 
Tổng 25 
4. Kết luận chung 
Trong bài báo này, chiến lược vét cạn được áp 
dụng để tìm ra kết quả cân bằng chuyền khi cho trước 
nhịp của dây chuyền. Trên cơ sở phân tích các điều 
kiện thực tế sản xuất tại nhà máy may Đồng Văn, tiến 
hành xác định các điều kiện ràng buộc về trình tự thực 
hiện, thiết bị và số lượng công nhân trong mỗi NCSX. 
Bước đầu các NCCN được phối hợp lại với nhau sao 
cho nhịp riêng của các NCSX thỏa mãn khoảng giới 
hạn nhịp, các ràng buộc về trình tự thực hiện và điều 
kiện ghép thiết bị, số lượng công nhân trong mỗi NCSX 
phải thỏa mãn. Có nhiều cách để phối hợp các NCCN 
thành NCSX mà vẫn thỏa mãn các điều kiện ràng buộc, 
trong các kết quả đó chọn ra các kết quả có số công 
nhân ít nhất để hiệu quả dây chuyền cao nhất có thể. 
Để thời gian làm việc của mỗi công nhân đồng đều 
nhau, bước tiếp theo tiến hành chọn trong các kết quả 
đó có số NCSX nằm trong khoảng giới hạn nhịp là 
nhiều nhất. Trong cách tiếp cận chiến lược vét cạn sẽ 
cho kết quả tối ưu. 
Sự thay đổi về nhịp của dây chuyền sẽ dẫn đến 
các kết quả cân bằng khác nhau, nó đòi hỏi phải cân 
bằng lại chuyền và tái phân bổ các nguồn lực. Kết quả 
nghiên cứu cho thấy khi thay đổi nhịp của dây chuyền 
sẽ cho các kết quả rất khác biệt. 
Do sự tiện ích trong sử dụng nên hiện nay nhu 
cầu tiêu thụ về nhóm chủng loại quần áo từ vải dệt kim 
nói chung và sản phẩm áo Polo-Shirt nói riêng là rất 
lớn trên thị trường thế giới và Việt Nam. Trong thực tế 
sản xuất sản phẩm này, sự thay đổi mặt hàng diễn ra 
thường xuyên do sự phong phú, đa dạng về kiểu dáng, 
kết cấu công nghệ may, thiết bị sản xuất. Do vậy, việc 
thiết lập một phần mềm giải quyết các bài toán cân 
bằng chuyền trong thực tế sản xuất là cần thiết. Tuy 
nhiên, nghiên cứu mới dừng lại ở việc xây dựng phần 
mềm cân bằng chuyền trong điều kiện thực tế sản xuất 
của nhà máy may Đồng Văn, cần phát triển bài toán 
cân bằng chuyền cho các hình thức tổ chức sản xuất 
của các chủng loại sản phẩm khác từ đó làm cơ sở cho 
việc xây dựng các phần mềm cân bằng dây chuyền 
theo đặc thù sản xuất ngành may công nghiệp. 
Lời cảm ơn 
Nhóm tác giả chân thành cảm ơn sự hỗ trợ của 
nhà máy may Đồng Văn, Tổng công ty CP Dệt May 
Hà Nội đã tạo điều kiện cho chúng tôi khảo sát, thực 
nghiệm để hoàn thành nghiên cứu này. 
Tài liệu tham khảo 
[1] N. Kriengkorakot and N. Pianthong, The assembly line 
balancing problem: Review Problem, Journal of 
Industrial Engineering, vol. 34 (2007) pp. 133–140. 
[2] S. Ghosh and R. J. Gagnon, A comprehensive literature 
review and analysis of the design, balancing and 
scheduling of assembly systems, International Journal 
of Production Research, vol. 27, no. 4 (1989) pp. 637–
670. 
[3] A. Scholl and C. Becker, State-of-the-art exact and 
heuristic solution procedures for simple assembly line 
balancing, European Journal of Operational Research, 
vol. 168, no. 3 (2006) pp. 666–693. 
[4] D. S. M. S. Santosh T. Ghutukade, Use of Ranked 
Position Weighted Method For Assembly Line 
Banlancing, International Journal of Advanced 
Tạp chí Khoa học và Công nghệ 141 (2020) 034-041 
41 
Engineering Research and Studies (2013) pp. 5–7. 
[5] V. V Pachghare and R. S. Dalu, Assembly Line 
Balancing Methods–A Case Study, International 
Journal of Science and Research vol. 3, no. 5 (2012) pp. 
2319–7064. 
[6] S. ERYÜRÜK, Clothing Assembly Line Design Using 
Simulation and Heuristic Line Balancing Techniques, 
Journal of Textile & Apparel/ Tekstil ve Konfeksiyon, 
no. 4 (2012), 360–368 
[7] A. Jayakumar and A. K. Krishnaraj, Productivity 
Improvement in Stitching Section of a Garment 
Manufacturing Company, International Journal of 
Innovative Research in Advanced Engineering, vol. 4, 
no. 12 (2017) pp. 8–11. 
[8] J. C. Chen, C.-C. Chen, L.-H. Su, H.-B. Wu, and C.-J. 
Sun, Assembly line balancing in garment industry, 
International Conference on Industrial Engineering and 
Operations Management Bali, Indonesia, January 7 – 9 
(2014) pp. 1215–1225. 
[9] Nguyễn Đức Nghĩa, Cấu trúc dữ liệu và thuật toán, 
NXB Đại học Bách khoa Hà Nội, 2013. 
[10] Tổng công ty Dệt May Hà Nội, Tài liệu kỹ thuật công 
nghệ sản phẩm áo Polo-Shirt, 2018.