Thực nghiệm bộ điều khiển tuyến tính hóa chính xác kết hợp khâu ước lượng nhiễu đầu vào theo nguyên lý tối ưu dọc trục thời gian cho trms trong phòng thí nghiệm

định ngay cả trong 
điều kiện nhiễu ngoài. 
Từ khóa: Tuyến tính hóa chính xác; ước lượng nhiễu đầu vào; tối ưu dọc trục thời gian; TRMS; 
Card dSPACE 1103. 
Ngày nhận bài: 22/4/2020; Ngày hoàn thiện: 21/5/2020; Ngày duyệt đăng: 25/5/2020 
AN EXPERIMENT FOR COMBINATION OF THE ACCURATE LINEAR 
CONTROLLER AND AN INPUT DISTURBANCE ESTIMATOR BASED ON 
TIME RECEDING OPTIMIZATION FOR TRMS IN THE LABORATORY 
Dam Bao Loc1*, Nguyen Duy Cuong2 
1Thai Nguyen Industrial College, 
2TNU - University of Technology 
ABSTRACT 
This paper focuses on the Twin Rotor Multi-Input Multi-Output (TRMS) system in the laboratory 
with an advanced controller. For the theoretical background, this proposed controller includes a 
linearized controller and an input disturbance estimator based on time receding optimization. Some 
main experimental equipments such as a computer, a dSP1103 card, a physical TRMS, external 
disturbance generating equipment (electric fans) and connection cables are used. The 
MATLAB/Simulink software was used to set the parameters for the controller and the Control 
Desk software was connected to the dSP1103 Card to communicate, calculate and control the 
TRMS. Experimental conditions are performed on real equipments in cases of reference signals 
with step and sinusoidal functions with an external disturbance (wind from the fan). Experimental 
results showed that the output signals quickly and accurately tracked to the reference signals and 
the system worked stably in conditions having external disturbance. 
Keywords: Accurate linearization; input disturbance estimator; time receding optimal; TRMS; 
dSPACE 1103 Card. 
Received: 22/4/2020; Revised: 21/5/2020; Published: 25/5/2020 
* Corresponding author. Email: dambaoloc@gmail.com 
Đàm Bảo Lộc và Đtg Tạp chí KHOA HỌC & CÔNG NGHỆ ĐHTN 225(06): 318 - 324 
 Email: jst@tnu.edu.vn 319 
1. Đặt vấn đề 
Nhìn chung, với một bộ điều khiển sau khi đã 
thiết kế và được chứng minh trên mô phỏng 
thì mục tiêu tiếp theo là phải kiểm nghiệm 
xem bộ điều khiển đó có thể áp dụng vào đối 
tượng thực hay không. Trong bài báo này sẽ 
đưa ra phương pháp cài đặt và kiểm nghiệm 
bộ điều khiển tuyến tính hóa chính xác kết 
hợp khâu bù nhiễu đầu vào dựa trên nguyên 
lý tối ưu dọc trục thời gian cho hệ thống Twin 
Rotor Multi-Input Multi-Output (TRMS) 
trong phòng thí nghiệm. Việc cài đặt dựa trên 
bộ thí nghiệm TRMS sẵn có đã được cài bộ 
điều khiển PID do nhà sản xuất cung cấp [1]. 
Trên máy tính cài đặt phần mềm 
Matlab/Simulink và phần mềm điều khiển 
Control Desk. Phần mềm Matlab/Simulink 
dùng để cài đặt bộ điều khiển với các thông 
số đã chọn. Card dSP1103 thông qua phần 
mềm điều khiển Control Desk để giao tiếp, 
xử lý và điều khiển TRMS. Trong thí 
nghiệm này tín hiệu mẫu là hàm đơn vị và 
hàm sin cho hệ thống TRMS. Ngoài ra, để 
đánh giá ảnh hưởng của nhiễu ngoài, hệ 
thống còn được thiết kế thêm bộ tạo nhiễu 
dùng quạt gió. 
2. Các thiết bị trên bàn thí nghiệm 
Hình 1 mô tả cấu trúc hệ thống thí nghiệm 
TRMS, gồm có máy tính, Card ghép nối 
dSPACE 1103, hệ thống Twin Rotor MIMO. 
Các thành phần được mô tả chi tiết trong 
các phần dưới đây. 
Hình 1. Cấu trúc vật lý của bàn thí nghiệm TRMS 
2.1. Máy tính 
- Cấu hình máy tính trong bàn thí nghiệm 
TRMS: Là loại Acer, có bộ vi xử lí Intel(R) 
Core(TM) i3-3220 CPU @ 3.30Ghz, RAM 
2.00GB, ổ cứng 500 GB 
- Máy tính được cài phần mềm Matlab 2012a 
và phần mềm ControlDesk 3.2.7 để giao tiếp, 
xử lý và điều khiển TRMS. 
2.2. Card dSPACE DS 1103 
Dùng cho kết nối, giao tiếp, đo các tín hiệu 
tương tác giữa máy máy tính và bộ biến đổi 
công suất. 
2.3. Hệ vật lý TRMS 
TRMS trong phòng thí nghiệm có mã hiệu 
TRMS 33-220 công ty thiết bị Feedback chế 
tạo gồm: 
- Khối nguồn đóng, cắt và bảo vệ quá tải. 
- Hai cánh quạt được truyền động bởi hai 
động cơ một chiều Maxon, mỗi động cơ có 
gắn máy phát tốc để lấy và đo vận tốc góc 
𝜔𝑣 , 𝜔ℎ và đưa tới khối ADC của Card 
dsPACE 1103. 
- Hai cánh quạt được gắn theo phương vuông 
góc với nhau trên cùng một cánh tay đòn. 
- Một thanh có gắn đối trọng được gắn vuông 
góc với cánh tay đòn tự do và cả hai cùng 
được gắn trên một trụ tại chốt quay. 
- Trên chốt quay có gắn hai sen sơ đo góc 
chao dọc và góc đảo lái , giá trị hai góc 
này đưa tới dSPACE 1103. 
2.4. Hệ thống tạo nhiễu ngoài 
Với mong muốn kiểm chứng hệ thống TRMS 
có khả năng ổn định trong điều kiện nhiễu 
ngoài, một bộ tạo nhiễu chủ động tác động lên 
hệ thống TRMS là một quạt gió (hình 2) đã 
được lắp thêm với các thông số: 
- Điện áp xoay chiều định mức: Uđm = 220/240V. 
- Công suất định mức: Pđm = 38 w. 
- Dòng định mức: Iđm = 0,22 A. 
- Tần số định mức: fđm = 50/60 Hz. 
Hình 3 là mô hình thực nghiệm TRMS có tại 
Viện nghiên cứu phát triển Công nghệ cao về 
d
S
P
A
C
E
 1
1
0
3
Đo lường
Điều khiển
Đàm Bảo Lộc và Đtg Tạp chí KHOA HỌC & CÔNG NGHỆ ĐHTN 225(06): 318 - 324 
320  Email: jst@tnu.edu.vn 
Kỹ thuật Công nghiệp thuộc Đại học Kỹ thuật 
Công nghiệp Thái Nguyên. 
Hình 2. Quạt gió tạo nhiễu chủ động. 
Hình 3. Mô hình bàn thí nghiệm TRMS 
3. Cài đặt bộ điều khiển 
3.1. Mô hình toán TRMS 
Mô hình toán của TRMS được sử dụng là mô 
hình toán chính xác dựa theo phương trình 
Euler_Lagrange [2]. 
[𝐽1𝑐𝑜𝑠
2𝛼𝑣 + 𝐽2𝑠𝑖𝑛
2𝛼𝑣 + ℎ
2(𝑚𝑇1+𝑚𝑇2) + 𝐽3]𝛼ℎ̈ 
+ℎ(𝑚𝑇1𝑙𝑇1𝑐𝑜𝑠𝛼𝑣 + 𝑚𝑇2𝑙𝑇2𝑠𝑖𝑛𝛼𝑣)�̇�𝑣
2 
+2𝛼ℎ̇𝛼�̇�(𝐽2 − 𝐽1)𝑠𝑖𝑛𝛼𝑣𝑐𝑜𝑠𝛼𝑣 = ∑ 𝑀𝑖ℎ𝑖 
(𝐽1 + 𝐽2)𝛼�̈� + ℎ(𝑚𝑇1𝑙𝑇1𝑠𝑖𝑛𝛼𝑣 − 𝑚𝑇2𝑙𝑇2𝑐𝑜𝑠𝛼𝑣)𝛼ℎ̈ 
+ �̇�ℎ
2(𝐽1 − 𝐽2)𝑠𝑖𝑛𝛼𝑣𝑐𝑜𝑠𝛼𝑣 + 
+𝑔(𝑚𝑇1𝑙𝑇1𝑐𝑜𝑠𝛼𝑣 + 𝑚𝑇2𝑙𝑇2𝑠𝑖𝑛𝛼𝑣) = ∑ 𝑀𝑖𝑣𝑖 
(1) 
Trong đó: 
𝛼𝑣 , 𝛼ℎ : Lần lượt là các góc chao dọc và góc 
đảo lái của cánh tay đòn tự do của TRMS với 
mặt phẳng ngang và mặt phẳng đứng. 
∑ 𝑀𝑖ℎ𝑖 : Tổng các mô men tác dụng trong 
chuyển động ngang, được tính: 
∑ Mihi = Mprop.h − Mfric,h − Mcable +
 +kmωv̇ cosαv 
𝑀𝑝𝑟𝑜𝑝.ℎ = 𝑙𝑡𝐹ℎ(𝜔ℎ)𝑐𝑜𝑠(𝛼𝑣): Mô men của 
lực đẩy của cánh quạt đuôi; 
𝑀𝑓𝑟𝑖𝑐,ℎ: Mô men ma sát của cánh tay đòn tự 
do trong chuyển động ngang. 
𝑀𝑓𝑟𝑖𝑐,ℎ = 𝑘𝑣𝑓ℎΩℎ + 𝑘𝑐𝑓ℎsign(Ωℎ) + 
+ {
𝑘𝑠𝑓ℎ 𝑘ℎ𝑖 Ωℎ = 0
+ 
−𝑘𝑠𝑓ℎ 𝑘ℎ𝑖 Ωℎ = 0
− 
 0 𝑡𝑟ườ𝑛𝑔 ℎợ𝑝 𝑘ℎá𝑐 
𝑀𝑐𝑎𝑏𝑙𝑒: Mô men của cáp dẹt 
𝑀𝑐𝑎𝑏𝑙𝑒 = {
𝑘𝑐ℎ𝑝𝛼ℎ 𝑛ế𝑢 𝛼ℎ ≥ 0
𝑘𝑐ℎ𝑛𝛼ℎ 𝑛ế𝑢 𝛼ℎ < 0
∑ 𝑀𝑖𝑣𝑖 : Tổng của các mô men trong chuyển 
động đứng , được tính: 
 ∑ 𝑀𝑖𝑣𝑖 = 𝑀𝑝𝑟𝑜𝑝.𝑣 − 𝑀𝑓𝑟𝑖𝑐.𝑣 + 𝑘𝑡𝜔ℎ̇ + 𝑀𝑔𝑦𝑟𝑜 
𝑀𝑝𝑟𝑜𝑝.𝑣 = 𝑙𝑚𝐹𝑣(𝜔𝑣): Mô men của lực đẩy do 
cánh quạt chính 
 𝑀𝑔𝑦𝑟𝑜 = 𝑘𝑔𝐹𝑣𝛺ℎ𝑐𝑜𝑠 𝛼𝑣: Mô men con quay 
hồi chuyển 
𝐹ℎ , 𝐹𝑣: Lực sinh ra bởi cánh quạt đuôi và cánh 
quạt chính 
 𝐹ℎ = {
𝑘𝑓ℎ𝑝ℎ|ℎ| 𝑘ℎ𝑖 ℎ ≥ 0
𝑘𝑓ℎ𝑛ℎ|ℎ| 𝑘ℎ𝑖 ℎ < 0
 𝐹𝑣 = {
𝑘𝑓𝑣𝑝𝑣|𝑣| 𝑘ℎ𝑖 𝑣 ≥ 0
𝑘𝑓𝑣𝑛𝑣|𝑣| 𝑘ℎ𝑖 𝑣 < 0
Đưa mô hình toán TRMS về dạng tổng quát 
hệ Euler_Lagrange [3-5]. 
M( q )q+C( q ,q )q+ g( q ) = Fτ+n(t) (2) 
Chuyển đổi mô hình Euler-Lagrange bất định 
(2) thành dạng Euler-Lagrange song tuyến bất 
định bằng cách đặt thành phần bất định mới: 
 ( , ) ( ) ( )= −d q t n t g q (3) 
Khi đó, mô hình Euler-Lagrange bất định ban 
đầu (2) trở thành: 
 M( q )q+C( q ,q )q = u+d( q ,t) (4) 
Ở đây =u , tức là ở đây ta cũng đã giả thiết 
cơ cấu chấp hành giống như một khâu biến 
đổi lý tưởng các giá trị vật lý.
( )
( )
( )
1 1 2 2
1 2
2 2
2 2
1 2
2
3
11
, , ( ) ( ) , 
( , ) ( , ) , , 1,2,
( cos sin )
( ) cos sin
(
(
)
, 
) 0 , 
i
ih
i
iv
i
T
T T v T T v
v v
h
ij
T T
v
j
M
M
q M q m q
C q q c q q i F I
g q m l m l
JJ
h m
j
g
m q
m J



=
=
 = = = 
= =
+
= +
+ + +
Đàm Bảo Lộc và Đtg Tạp chí KHOA HỌC & CÔNG NGHỆ ĐHTN 225(06): 318 - 324 
 Email: jst@tnu.edu.vn 321 
( )
( )
( )
( )
1 1 2 2
1 1 2 2
12 21
22 1 2
11 2 1
12
21 1 2
22
( ) ( )
sin cos , 
( ) ,
( , ) sin cos
( , ) cos sin
( , ) sin cos 
0.
2
T T T T
v v v
v T T v T T v
h v v
v v
m q m q
m q J J
c q q J J
q
h m l m l
hc q q
c q J
m l m l
J
c
−
= =
=
= +
= −
= +
= −
=
Bảng 1. Tham số thực nghiệm cho hệ TRMS 
Ký hiệu Giá trị Đơn vị 
h 0,06 m 
1T
m 0,8250 kg 
2T
m 0,0908 kg 
1T
l 0,0186 m 
2T
l 0,2443 m 
1J 0,0591 kgm2 
2J 0,0059 kgm2 
3J 1,68x10-5 kgm2 
g 9,81 m/s2 
Hình 4 là cấu trúc hệ thống điều khiển cho hệ 
TRMS có mô hình toán học dạng Euler- 
Lagrange. Đây là hệ thống điều khiển kết hợp 
giữa bộ điều khiển tuyến tính hóa chính xác 
và bộ nhận dạng bất định. Các thành phần của 
hệ thống điều khiển này sẽ được trình bày cụ 
thể ở mục 3.2 và 3.3. 
Hệ TRMS 
dạng Euler- 
Lagrange
u ( , )x col q q=
Nhận dạng 
bất định
d 
d
Bộ điều 
khiển TTH
r
Hình 4. Điều khiển kết hợp tuyến tính hóa chính 
xác và bù bất định 
3.2. Bộ điều khiển tuyến tính hóa 
  1 2( ) ( , )u M q r K e K e C q q q= + + + (5) 
với = −e r q . 
Hai ma trận đối xứng xác định dương 
1 2,K K thỏa mãn: 
2
1 1 2 2 2 1diag( ), diag( ) 0= = i i i iK k K k k k víi 
3.3. Khối ước lượng nhiễu 
Dùng để ước lượng nhiễu d theo nhiễu hệ 
thống d dựa trên nguyên lý tối ưu dọc trục 
thời gian [6]. 
4. Thực nghiệm 
Cấu trúc hệ thống điều khiển hệ thực TRMS 
được thiết kế trên Simulink (hình 5), gồm có 
các thành phần: 
- SVF1, SVF2: Các bộ lọc biến trạng thái, đây 
là khâu bậc hai. 
- Bộ điều khiển tuyến tính hóa chính xác: dùng 
để tính tín hiệu điều khiển mô men. 
- PID, PIDi: Các mạch vòng phản hồi âm tốc 
độ và âm dòng điện tương ứng cho động cơ 
đuôi và động cơ chính. 
- TRMS vật lý: Liên kết Card dspace 1103 
với Simulink thông qua phần mềm điều khiển 
Control Desk. 
- Khối ước lượng nhiễu: Xác định nhiễu nhiễu 
và bù nhiễu 1d , 2d tương ứng theo mặt phẳng 
ngang và mặt phẳng đứng. 
- Khối bù bhM , bvM : Dùng để tìm ra mô 
men lực đẩy của cánh quạt chính và cánh quạt 
đuôi, sau đó dựa vào mối liên hệ giữa mô men 
lực đẩy và tốc độ góc tương ứng của các động 
cơ đuôi và động cơ chính. Quá trình này được 
thực hiện như sau:
Đàm Bảo Lộc và Đtg Tạp chí KHOA HỌC & CÔNG NGHỆ ĐHTN 225(06): 318 - 324 
322  Email: jst@tnu.edu.vn 
 Hình 5. Cấu trúc hệ thống điều khiển hệ thực TRMS thiết kế trên Simulink 
Từ công thức (1) đặt: 
 , - cosfric h cable m vbh vM M M k  = − + (6) 
ta sẽ có: 
.prop h ih
i
hbM M M
−=
 (7) 
và 
.
.
.
.
.
khi cos 0
cos
0 khi cos 0
khi cos 0
cos
 
 − 
= = 
prop h
prop h v
t fhn v
h prop h v
prop h
prop h v
t fhp v
M
M
l k
M
M
M
l k
 (8) 
Tương tự, từ (1), đặt: 
 .fric v t gyrbv ohM M k M− + += (9) 
sẽ được: 
 .prop v iv
i
vbM M M
−=
 (10) 
và
.
.
.
.
.
khi 0
0 khi 0
khi 0

= = 
− 
prop v
prop v
m fvp
v prop v
prop h
prop v
m fvn
M
M
l k
M
M
M
l k
 (11) 
Vector tín hiệu mẫu 1 2( , )=
Tr r r cho hai 
góc ( , ) = Th vq cần phải bám theo vẫn 
được chọn là hằng số và dạng hình sin: 
Trường hợp tín hiệu mẫu là hằng số: 
1 0,5 [rad]h r → = 2 0,3 [rad]v r → = 
Trường hợp tín hiệu mẫu dạng hình sin: 
1 0,2sin(0,1256 ) [rad]h r t → = 
2 0,2sin(0,1256 ) [rad]v r t → = − 
 Bộ điều khiển tuyến tính hóa chính xác, có 
hai ma trận 1 2,K K được chọn lần lượt là: 
1
40 0
0 40
= 
K ; 2
30 0
0 30
= 
K 
Thông số các bộ điều khiển PID cho cơ cấu 
chấp hành là: 
- Thông số bộ điều khiển tốc độ và dòng điện 
cho động cơ đuôi: 
5 6
, ,
6
,
, ,
,
PID : 10 ; 10 
 35 10 .
PID : 0,25; 20 
0,0028
h h h
h
t t t
t
p I
d
i p i I i
d i
K K
K
K K
K
  

− −
−
= =
= 
= =
=
- Thông số bộ điều khiển tốc độ và dòng điện 
cho động cơ chính: 
6 5
, ,
6
,
, ,
,
PID : 4 10 ; 5 10
 15 10
PID : 0,1; 80
0,0005
v v v
v
v v v
v
p I
d
i p i I i
d
K K
K
K K
K
  


− −
−
= = 
= 
= =
=
Đàm Bảo Lộc và Đtg Tạp chí KHOA HỌC & CÔNG NGHỆ ĐHTN 225(06): xx - xx 
 Email: jst@tnu.edu.vn 323 
Các tham số PID này đã được lựa chọn trên cơ 
sở phương pháp Ziegler–Nichols thứ 2. 
Tiến hành chạy thực nghiệm được kết quả như 
trên hình 6 đến hình 15. 
Hình 6. Đáp ứng góc đảo lái ứng với tín hiệu mẫu 
0,5hR = cùng sai lệch khi có nhiễu ngoài 
Hình 7. Đáp ứng góc chao dọc ứng với tín hiệu 
mẫu 0,3vR = cùng sai lệch khi có nhiễu ngoài. 
Hình 8. Nhiễu ước lượng ( )hd t ứng với tín hiệu 
mẫu 0,5hR = khi có nhiễu ngoài 
Hình 9. Nhiễu ước lượng ( )vd t ứng với tín hiệu 
mẫu 0,3vR = khi có nhiễu ngoài 
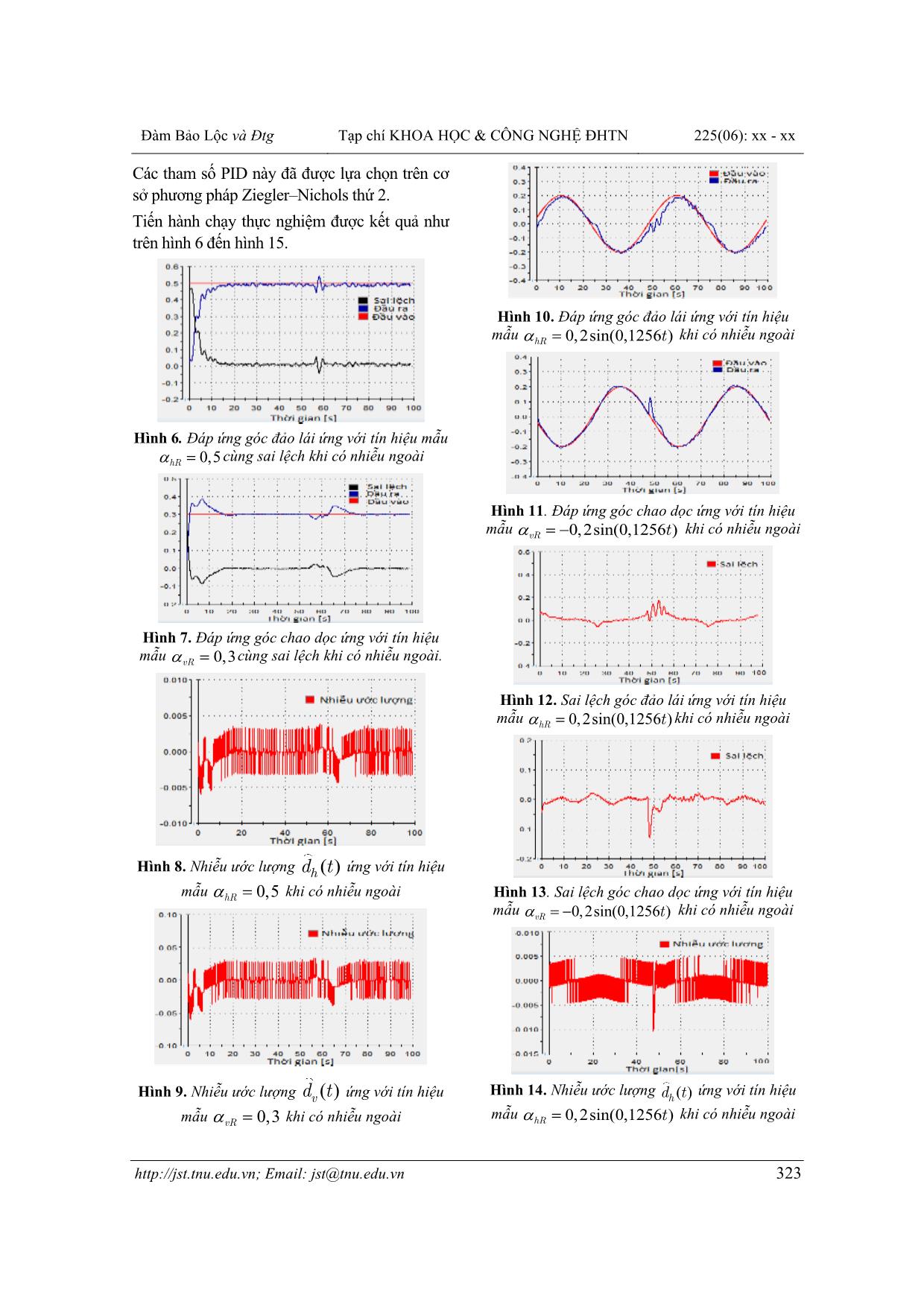
Hình 10. Đáp ứng góc đảo lái ứng với tín hiệu 
mẫu 0,2sin(0,1256 )hR t = khi có nhiễu ngoài 
Hình 11. Đáp ứng góc chao dọc ứng với tín hiệu 
mẫu 0,2sin(0,1256 )vR t = − khi có nhiễu ngoài 
Hình 12. Sai lệch góc đảo lái ứng với tín hiệu 
mẫu 0,2sin(0,1256 )hR t = khi có nhiễu ngoài 
Hình 13. Sai lệch góc chao dọc ứng với tín hiệu 
mẫu 0,2sin(0,1256 )vR t = − khi có nhiễu ngoài 
Hình 14. Nhiễu ước lượng ( )hd t ứng với tín hiệu 
mẫu 0,2sin(0,1256 )hR t = khi có nhiễu ngoài 
Đàm Bảo Lộc và Đtg Tạp chí KHOA HỌC & CÔNG NGHỆ ĐHTN 225(06): 318 - 324 
324  Email: jst@tnu.edu.vn 
Hình 15. Nhiễu ước lượng ( )vd t ứng với tín hiệu 
mẫu 0,2sin(0,1256 )vR t = − khi có nhiễu ngoài 
Hình 6 đến hình 15 là kết quả thực nghiệm 
khi có nhiễu ngoài là quạt gió từ thời điểm
( )50 100= t s . Tại thời điểm 50 [ ]=t s , 
nhiễu ngoại lực ảnh hưởng khá mạnh đến hệ 
thống, tuy nhiên nhờ cơ cấu bù nhiễu mà đáp 
ứng đầu ra nhanh chóng bám tín hiệu mẫu. 
Điều này có thể thấy rõ qua các nhiễu ước 
lượng 1 2,d d phản ứng nhanh chóng với nhiễu 
ngoài (hình 8, hình 9, hình 14 và hình 15). 
5. Kết luận 
Trong bài báo này, nhóm tác giả đã trình bày 
việc cài đặt và kiểm nghiệm bộ điều khiển 
tuyến tính hóa chính xác kết hợp khâu bù 
nhiễu đầu vào dựa trên nguyên lý tối ưu dọc 
trục thời gian cho hệ thống Twin Rotor Multi-
Input Multi-Output (TRMS). Kết quả thực 
nghiệm với tín hiệu mẫu là hàm đơn vị và 
hàm sin cho thấy tín hiệu đầu ra nhanh chóng 
bám tín hiệu mẫu, hệ thống làm việc ổn định 
ngay cả khi có nhiễu ngoài tác động. 
TÀI LIỆU THAM KHẢO/ REFERENCES 
[1]. Twin Roto MIMO System Control 
Experiments 33-949S Feedback Instruments 
Ltd, East susex, U.K., 2006. 
[2]. A. Rahideh, and M. H. Shahee, “Mathematical 
dynamic modeling of a twin- rotor multiple 
input – multiple output System,” Proceedings 
of the IMechE, Part I: Journal of Systems and 
Control Engineering, vol. 221, pp. 89-101, 
2006. 
[3]. David Morin, Introduction to Classical Mechanics: 
With Problems and Solutions. Cambridge 
University, 2008. 
[4]. R. Ortega, A. Loria, P. J. Nicklasson, and H. 
S. Ramirez, Passivity−bassed Control of 
Euler-Lagrange Systems. Springer Verlag, 
1998. 
[5]. F. L. Lewis, D. M. Dawson, and C. T. Abdallah, 
Robot Manipulator Control. Theory and Practice. 
Marcel Dekker, Inc, 2004. 
[6]. D. P. Nguyen, and H. N. Nguyen, “Some 
methods of controlling the mechanical system 
have the uncertain Euler-Lagrange model,” 
(in Vietnamese) Collection of papers in the 
first National Scientific Conference on 
Dynamics and Control, Da Nang, July 19-20, 
2019, doi: 10.15625/vap.201900026.