Tài liệu Bồi dưỡng thường xuyên dành cho giáo viên THPT môn Tin học
Adobe Connect là hệ thống cho phép thực hiện:
- Họp qua web (Web Conference),
- Lớp học ảo (Virtual Classroom),
- Chia sẻ bài giảng điện tử eLearning để học trực tuyến, tạo lớp học và
chương trình học.
Hệ thống Adobe Connect do Cục CNTT, Bộ Giáo dục và Đào tạo thiết lập
và quản lý, có địa chỉ website là . Hiện nay, có nhiều phòng
họp ảo khác nhau, tương ứng phần đuôi của địa chỉ khác nhau. Tại một thời điểm,
tổng số người có thể nối vào hiện nay là 80 concurent user licenses. Để tham gia
một phòng họp hay lớp học, người sử dụng cần biết địa chỉ phòng họp. Thí dụ:
là phòng họp đã được giao cho Sở GD&ĐT
Quảng Bình quyền quản lý.
1. Các tính năng chính
- Phát hình video: người giảng bài.
- Phát tiếng (voice, sound).
- Trình chiếu powerpoint.
- Trình chiếu chia sẻ màn hình các ứng dụng khác.
- Trình chiếu chia sẻ màn hình windows.
- Cửa sổ trao đổi qua gõ phím (Chatting room).
- Thăm dò dư luận, bỏ phiếu (Polling, Vote).
- Bảng trắng để vẽ, viết
- Truyền tệp (file transfer).
- Cộng tác, làm việc chung.
- Diễn đàn trao đổi.
- Kiểm tra kiến thức bằng thi trắc nghiệm.
2. Ứng dụng của web conference
- Họp giao ban giữa Bộ với các Sở; giữa Sở với các Phòng; giữa Phòng với
các trường quận/huyện.
- Tập huấn phần mềm (có thể chia sẻ màn hình phần mềm cần tập huấn).
- Giảng bài từ xa.
- Chia sẻ bài giảng eLearning.
- Bảo vệ luận án.
- Giao lưu giữa các trường trong và ngoài nước.
- Quảng cáo giới thiệu sản phẩm.2
3. Điều kiện sử dụng:
- Có đường kết nối Internet ADSL.
- Có webcam nếu muốn hiển thị hình ảnh video của mình lên
cho mọi người nhìn thấy.
- Có microphone (có thể tích hợp sẵn ở trong webcam như Logitech
Quickcam).
- Loa máy tính.
- Được thông báo địa chỉ web để họp (Cục CNTT cấp).
4. Các quyền sử dụng:
- Host: làm ông chủ, có đầy đủ quyền điều hành. Người làm host có thể:
+ Cho phép các thành viên đều là presenter như sau:
+ Không cho ai vào nữa (block Incoming Attendees)
+ Không cho khách là gust vào (block Guest Attendees), trong khi các
thành viên khác đã đăng ký vẫn được vào.
Cục CNTT cấp quyền cho người làm host.
- Presenter: Người trình bày, báo cáo viên.
- User: Người sử dụng, đại biểu, người học.

Trang 1

Trang 2

Trang 3
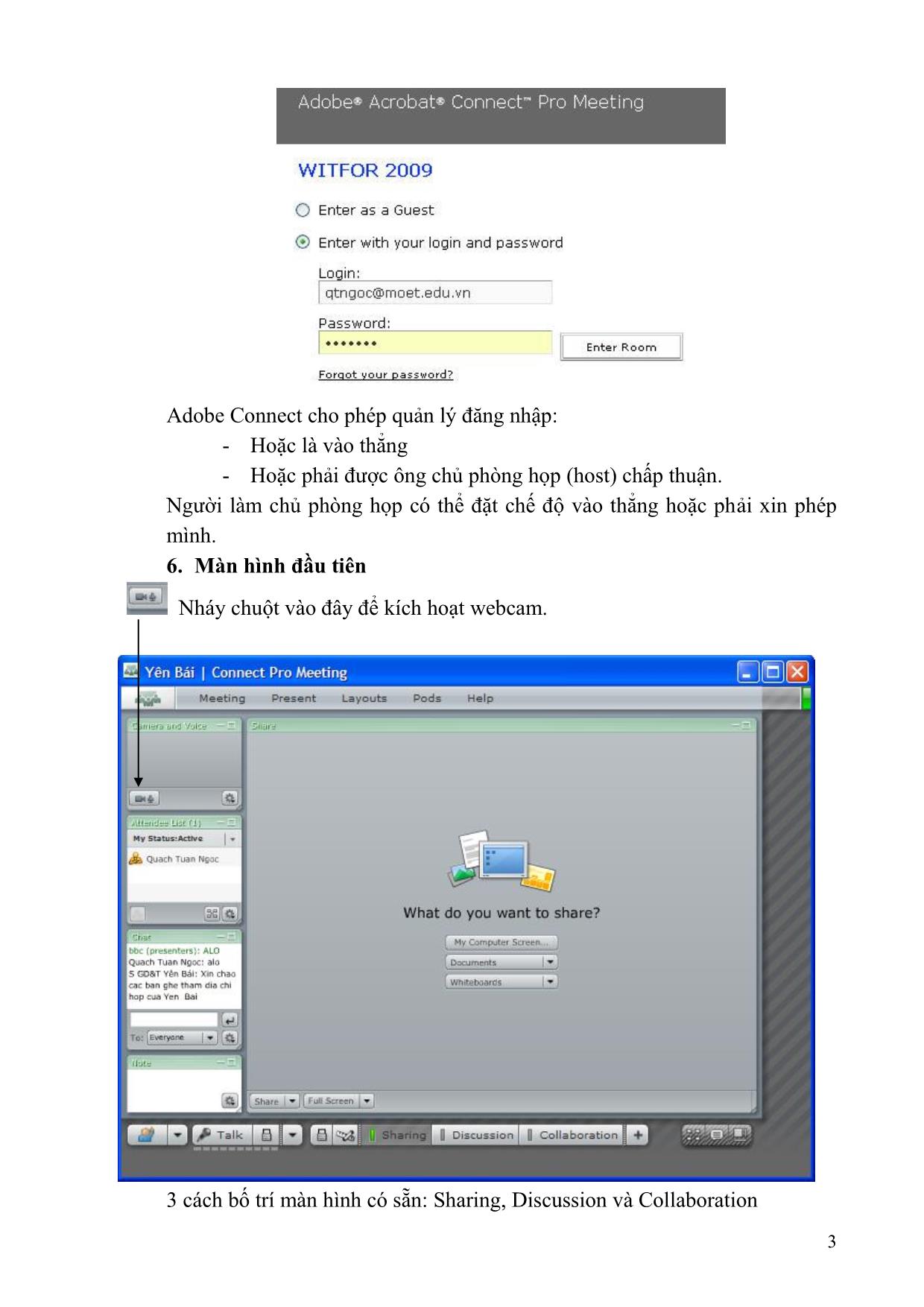
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
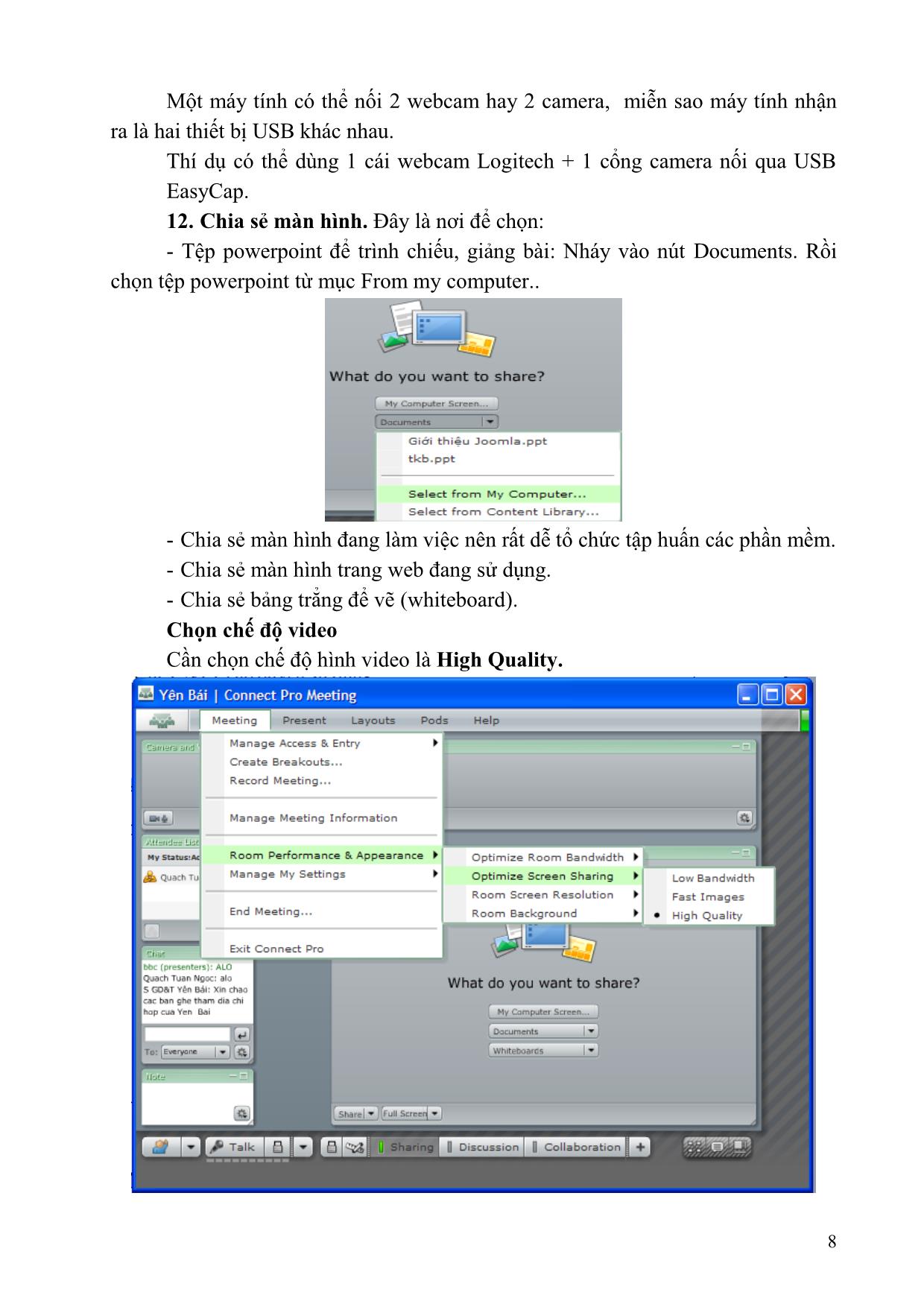
Trang 9
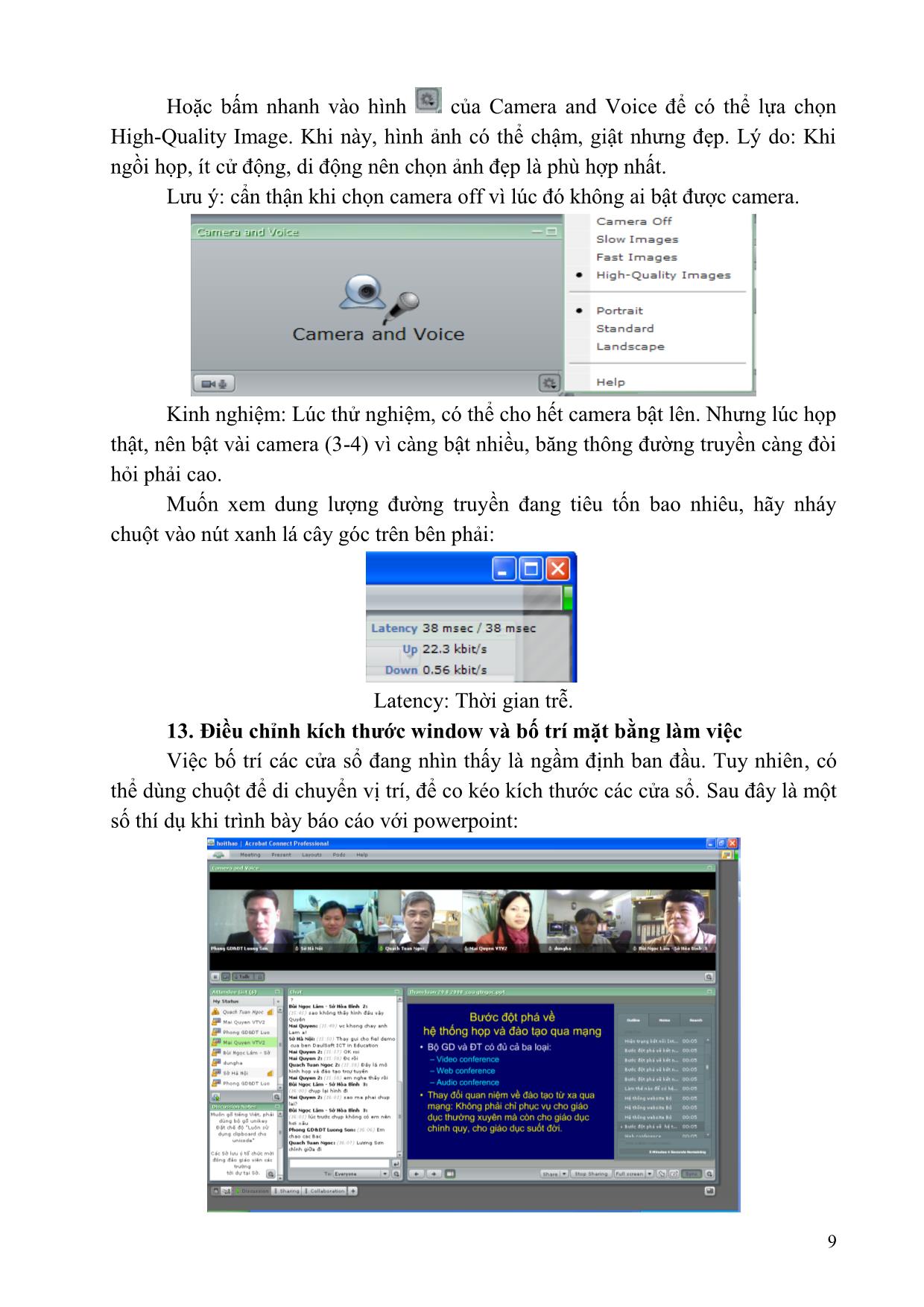
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Tài liệu Bồi dưỡng thường xuyên dành cho giáo viên THPT môn Tin học

nh toán của các nhà chuyên
môn sau khi đã chạy được P km xe nên dừng lại cho hành khách nghỉ ở một khách
sạn. Vì thế, nếu xe dừng lại cho khách nghỉ ở khách sạn sau khi đã đi được Q km
thì lái xe phải trả một lượng phạt là (Q-P)2.
Yêu cầu : Hãy xác định xem trên tuyến đường đến khách sạn thứ n xe cần dừng lại
nghĩ ở những khách sạn nào để tổng lượng phạt mà lái xe phải trả là nhỏ nhất .
Dữ liệu vào: Cho trong file văn bản có tên BL3.INP:
- Dòng 1: chứa số nguyên dương n (n<=10000).
- Dòng 2: chứa số nguyên dương P (P<=500).
- Dòng 3: chứa n số nguyên dương a[1],a[2],..a[n] (hai số liên tiếp trên dòng
được ghi cách nhau bởi dấu cách) (a[i]<=2000000, i=1,2..n).
Dữ liệu ra: Ghi ra file văn bản BL3.OUT:
- Dòng 1: ghi Z là lượng phạt mà lái xe phải trả .
- Dòng 2: ghi chỉ số của K khách sạn mà xe dừng lại cho khách nghỉ (trong đó
nhất thiết bao gồm cả chỉ số của khách sạn thứ n ).
BL3.INP BL3.OUT
4
300
250 310 550 590
500
2 4
2.1.2. Phân tích: Ta thường phân tích, thiết kế và giải quyết như sau:
- Gọi P(i) là bài toán du lịch vòng quanh thế giới khi có i khách sạn.
38
- Vậy bài toán ban đầu là P(n).
- Trong bài toán ta cần phải xác định:
+qh[i] là tổng tiền phạt ít nhất nếu dừng ở khách sạn i, ta cần tìm qh[n].
+x[i] là khách sạn phải dừng cho khách nghỉ.
- Trường hợp khi i=1
+qh[i]:=SQR(a[1]-P);
+x[i]:=1;
- Trường hợp khi i>1
+ Nếu nghỉ tại KS i ngay sau khi nghỉ tại KS 1, chi phí là: (a[i]-a[1]-P)2+qh[1]
+ Nếu nghỉ tại KS i ngay sau khi nghỉ tại KS 2, chi phí là: (a[i]-a[2]-P)2+qh[2]
......
+ Nếu nghỉ tại KS i ngay sau khi nghỉ tại KS j, chi phí là: (a[i]-a[j]-P)2+qh[j]
Vậy qh[i]:=MIN{(a[i]-a[j]-P)2+qh[j] / j=1..i-1}
x[i]=j mà tại đó qh[i] đạt max.
- Theo phân tích như trên ta có đoạn chương trình thể hiện thuật toán như sau:
Procedure Vong_quanh_the_giơi;
Var i,j :Integer; Min : Real;
Begin
Qh[0]:=0;
For i:=1 to n do
Begin
Min:=10000000000000000000.0;
For j:=i-1 downto 0 do
If min<sqr(a[i]-a[j]-P)+qh[j] then
min:=sqr(a[i]-a[j]-P)+qh[j];
Qh[i]:=min;
End;
End;
1.1.3. Đánh giá và cải tiến
Theo cách phân tích và cài đặt như trên thì chương trình chạy rất chậm với
độ phức tạp O(n2 /2). Để tăng tốc độ thuật toán ta có mệnh đề sau :
Mệnh đề: Giả sử với vị trí i ta tìm được ji là vị trí mà tại đó qh[i] đạt min. Khi xét
vị trí i+1 nếu qh[i+1] đạt min tại ji+1 thì ta luôn có ji+1 [ji,i].
Chứng minh:
Giả sử ta đang xét vị trí i
Đặt : Fi(j) = (a[i]-a[j]-P)2+qh[j] ;
Như vậy Qh[i]=MIN{Fi(j) , j = 0,1,2...,i-1}.
39
Xét hai vị trí 0<=k<j<i . Ta có
Nếu Fi(j)>=Fi(k)
Fi(j)-Fi(k)>=0
(a[i]-a[j]-P)2+qh[j]- (a[i]-a[k]-P)2-qh[k]>=0
qh[j]-qh[k]-(2*a[i]-2*p-a[j]-a[k])*(a[j]-a[k])>=0
(qh[j]-qh[k])/ (a[j]-a[k])>=(2*a[i]-2*p-a[j]-a[k]) (vì a[j]-a[k]>0 )
(qh[k]-qh[j])/( a[k]-a[j])+a[j]+a[k]>=2*a[i]-2*p;
Đặt : Gt(k,j)= (qh[k]-qh[j])/( a[k]-a[j])+a[j]+a[k] (k<j).
Vậy Fi(j)>=Fi(k) Gt(k,j)>=2*(a[i]-p). (1)
Tương tự Fi(j)<=Fi(k) Gt(k,j)<= 2*(a[i]-p). (2)
Theo mệnh đề:
Xét tại vị trí i: nếu 0<=k<j<i thì ji sao cho Fi(ji)<= Fi(k) với k [0,i-1] .
Xét tại vị trí i+1: nếu 0<=k<j<i thì ji+1 mà ji<ji+1<i
sao cho Fi+1(ji+1)<= Fi+1(k) với k [0,i-1] , suy ra Fi+1(ji+1)<= Fi+1(ji). (3)
Ta phải chứng minh ji+1>ji
0 ji+1 ji i i+1
Thật vậy:
Giả sử ji+1<ji . Ta có Fi(ji)<=Fi(ji+1) Gt(ji+1,ji)<= 2*(a[i]-p)
Vì a[i]<a[i+1] nên Gt(ji+1,ji)<= 2*(a[i+1]-p)Fi+1(ji)<= Fi+1(ji+1) mâu thuẫn (3)
Vậy ji+1 [ji,i] đpcm.
Áp dụng mệnh đề 1, ta có thể cải tiến thuật toán trên như sau :
Procedure Cai_tien_VQTG;
Var i,j,vt,vt1 : Integer; Min : Real;
Begin
Qh[0]:=0; vt1:=0;
For i:=1 to n do
Begin
Min:=10000000000000000000.0;
For j:=i-1 downto vt1 do
If min<sqr(a[i]-a[j]-P)+qh[j] then
Begin
min:=sqr(a[i]-a[j]-P)+qh[j];
vt:=j;
End;
Vt1:=vt;
40
Qh[i]:=min;
End;
End;
Với cách cài đặt như trên thì tốc độ chương trình sẽ tăng từ 100-150 lần.
Nhưng ta lại thấy rằng nếu cho P rất lớn cở vài chục triệu (theo đề bài thì P<=500)
thì tốc độ của thuật toán này cũng chưa đáp ứng được yêu cầu về thời gian. Vì thế
ta có thêm một kỹ thuật cải tiến tổng quát với độ phức tạp là O(2n). Xét mệnh đề
sau:
1.1.4. Bài tập có cách tinh chỉnh tương tự: Phân trang
Văn bản là một dãy gồm N từ đánh số từ 1 đến N. Từ thứ i có độ dài là wi
(i=1, 2, ..., n). Phân trang là một cách xếp lần lượt các từ của văn bản vào dãy các
dòng, mỗi dòng có độ dài L, sao cho tổng số độ dài của các từ không vượt quá L.
Ta gọi hệ số phạt của một dòng trong cách phân trang là hiệu số L-K, trong đó K là
tổng độ dài của các từ xếp trên dòng đó. Hệ số phạt của các phân trang là tổng giá
trị các hệ số phạt của các dòng.
Yêu cầu: Tìm cách phân trang với hệ số phạt nhỏ nhất.
Dữ liệu vào: Cho trong file PTRANG.INP có cấu trúc như sau:
- Dòng 1: Chứa hai số nguyên dương N L (N<=4000, L<=70)
- Dòng thứ i trong N dòng tiếp theo: chứa số nguyên dương wi (wi<=L), i=1...n.
Dữ liệu ra: Ghi ra file PTRANG.INP theo cấu trúc như sau:
- Dòng 1: Ghi hai số nguyên dương P Q là hệ số phạt và số dòng theo cách phân
trang tìm được.
- Dòng thứ i trong Q dòng tiếp theo: ghi chỉ số của các từ trong dòng thứ i của cách
phân trang.
Các giá trị số trên một dòng được ghi cách nhau ít nhất một dấu cách.
2.2. Ví dụ 2
2.2.1. Bài toán: Bố trí hội thảo
Có N cuộc họp đánh số từ 1 đến N đăng ký làm việc tại một phòng hội thảo.
Cuộc họp i cần được bắt đầu tại thời điểm Ai và kết thúc tại thời điểm Bi (i=1, 2,
..., N). Hai cuộc họp bất kỳ chỉ được nhận phục vụ nếu các khoảng thời gian làm
việc tương ứng chỉ có thể giao nhau tại đầu mút. Hãy tìm một lịch cho phòng hội
thảo để có thể phục vụ được nhiều cuộc họp nhất.
Dữ liệu vào: Được cho trong file BOTRI.INP theo cấu trúc như sau:
+ Dòng 1: Ghi số N (N<10000)
+ Dòng thứ i trong số N dòng tiếp ghi 2 số nguyên Ai và Bi cách nhau ít nhất
một dấu cách. (1<= Ai, Bi <=32000)
Dữ liệu ra: Ghi ra file BOTRI.OUT theo cấu trúc như sau:
41
+ Dòng 1: Ghi số K là số cuộc họp tối đa có thể bố trí được,
+ K dòng tiếp, mỗi dòng ghi số hiệu của cuộc họp được phục vụ theo trình tự
lịch bố trí.
Thí dụ:
BOTRI.INP BOTRI.OUT
5
1 3
2 4
1 6
3 5
7 9
3
1
4
5
2.2.2. Phân tích
Chợt thấy bài toán không có dạng của quy hoạch động, bởi vì tại bước thứ i
để xét cuộc họp thứ i ta không chỉ dựa vào các cuộc họp từ 1 đến i-1 mà còn phải
xét đến các cuộc họp từ i+1 đến n, điều này là do theo thứ tự đăng ký thời điểm bắt
đầu cuộc họp không tăng dần.
Tuy nhiên chỉ cần một đoạn chương trình sắp xếp ta sẽ quy được thời điểm
bắt đầu cuộc họp tăng dần. Đương nhiên, trong khi sắp xếp ta phải lưu lại chỉ số
của mỗi cuộc họp.
Giả sử Ai được sắp xếp tăng dần, ta thường phân tích bài toán như sau:
- Gọi P(i) là bài toán bố trí cuộc họp i vào danh sách cuộc họp.
- Trong bài toán ta cần xác định:
+F(i): là số lượng cuộc họp nhiều nhất khi bố trí thêm cuộc họp i +T(i):
là chỉ số cuộc họp có thể bố trí được trước cuộc họp thứ i.
- Trường hợp khi i=1:
+F[1]:=1;
+T[1]:=0;
- Trường hợp khi i>1:
+Nếu bổ sung cuộc họp i sau cuộc họp 1 thì F[i]:=F[1]+1;
+Nếu bổ sung cuộc họp i sau cuộc họp 2 thì F[i]:=F[2]+1;
...
+Nếu bổ sung cuộc họp i sau cuộc họp j thì F[i]:=F[j]+1;
Vậy F[i]:=Max{F[j]+1 / j:=1..i-1}
T[i]:=j; mà tại đó F[i] đạt max
- Với sự phân tích như trên ta có thuật giải để tìm F[i] và T[i] như sau;
Procedure QHD_BOTRI
Begin
42
-Sắp xếp tăng dần theo A[i]
-Đối với mỗi cuộc họp thứ i (i:=2..n), ta thực hiện:
So sánh cuộc họp i với tất cả các cuộc họp j (j:=1..i-1)
Nếu B[j]<=A[i] và F[i]<F[j]+1 thì
F[i]:=F[j]+1;
T[i]:=j;
-Tìm M=Max(F[i]) (i:=1..n) chính là số cuộc họp lớn nhất cần tìm.
-Vị trí i mà tại đó F[i] đạt max là cuộc họp cuối cùng phải bố trí.
Sử dụng T[i] để tìm cuộc họp bố trí ngay trước i.
End;
2.2.3. Đánh giá
Về mặt dữ liệu, chương trình phải sử dụng bốn biến mảng một chiều (A[n],
B[n], F[n] và T[n]. Về mặt thời gian, ta thấy rằng thuật giải trên có độ phức tạp
O(N2/2). Khi N=10000 thì chương trình sẽ chạy rất chậm.
2.2.4. Cải tiến
Phương án đưa ra nhằm cải tiến hoàn toàn thuật giải để độ phức tạp trở
thành O(N)
Về mặt dữ liệu, ta chỉ cần sử dụng hai mảng F[32000] và T[32000]. Trong
đó F[i] có nghĩa là cuộc họp có thời điểm đầu là i và thời điểm cuối là F[i], T[i] là
chỉ số của cuộc họp theo thứ tự được đọc.
Về mặt thuật giải:
Bước 1: Ta thực hiện đọc từng dòng của file theo cặp (a,b) và gán F[a]:=b;
T[a]:=i; Chú ý: nếu hai cuộc họp có thời điểm đầu bằng nhau thí cuộc họp nào có
thời điểm cuối nhỏ sẽ được chọn.
Bước 2: Tại ô thứ i của F, tìm giá trị nhỏ nhất trong đoạn từ i đến F[i]:
M=min(F[j]) (j:=i..F[i]). Sau đó lặp lại bước 2 đối với ô thứ M
Chương trình được viết trên thuật toán này có tốc độ chạy nhanh hơn rất
nhiều so với thuật toán quy hoạch động đã trình bày trên. Điều này đã cho thấy
rằng, một số bài toán sử dụng phương pháp quy hoạch động lại cho hiệu quả kém
hơn phương pháp bình thường khác.
43
KẾT LUẬN
Khi lập trình giải quyết bài toán, không gian nhớ là rất quan trọng. Một bài
toán được giải quyết tối ưu nếu nó sử dụng tối thiểu không gian nhớ. Việc tinh
chỉnh để giảm không gian nhớ là một điều cần thiết. Trong một số bài toán quy
hoạch động, ta có thể dễ dàng nhận thấy phần không gian nhớ lãng phí nên việc
tinh chỉnh cũng khá đơn giản và không làm thay đổi nhiều về thuật giải (như ở ví
dụ 1). Tuy nhiên, trong một số bài toán khác, để chuyển từ mảng hai chiều thành
mảng một chiều lại làm bài toán trở nên khó hơn và cũng kéo theo thời gian thực
hiện chương trình tăng lên (như ở ví dụ 2 và ví dụ 3). Vì vậy, tùy theo yêu cầu về
không gian dữ liệu vào ra để ta lựa chọn phương pháp tính chỉnh cho phù hợp.
Thời gian thực hiện chương trình cũng là một yếu tố liên quan đến tính tối
ưu của chương trình. Rõ ràng việc tinh chỉnh nhằm giảm thời gian thực hiện
chương trình là rất cần thiết, nó làm giảm chi phí thực hiện chương trình, đặc biệt
trong nhiều bài toán yêu cầu xử lý thời gian thực. Để giảm thời gian thực hiện
chương trình, người ta thường phải lưu lại kết quả trung gian để không cần phải
tính lại nhiều lần một kết quả. Điều này cũng đồng nghĩa với việc tăng không gian
nhớ, đồng thời cũng có thể làm thay đổi hoàn toàn thuật toán. Tiểu luận đã trình
bày một kỹ thuật nhằm làm giảm được rất nhiều thời gian thực hiện chương trình
nhưng không gian nhớ không tăng hoặc tăng lên không đáng kể. Không phải bất cứ
bài toán nào cũng có cùng một kỹ thuật tinh chỉnh mà mỗi dạng bài có một kỹ
thuật khác nhau. Không phải dễ dàng để làm được điều này, nó đòi hỏi người lập
trình phải phân tích và thiết kế thật kỹ lưỡng và kết hợp với những suy luận toán
học.
44
PHỤ LỤC
1. Cài đặt chi tiết của bài toán Sinh viên ôn thi:
const fi='onthi.inp';
fo='onthi.out';
type mhc=array[0..100,0..100] of integer;
mmc=array[0..100] of integer;
var g:text;
m,n:word;
x,a:mhc; f1,f2:mmc;
procedure doc;
var i,j:word;
begin
assign(g,fi);
reset(g);
readln(g,n,m);
for i:=1 to n do
begin
for j:=1 to 3 do read(g,a[i,j]);
readln(g);
end;
close(g);
end;
procedure xl;
var i,j,k:word;
begin
fillchar(f1,sizeof(f1), 0);
fillchar(f2,sizeof(f2), 0);
fillchar(x,sizeof(x), 0);
for i:=1 to n do begin f1[i]:=a[i,1];x[i,1]:=i;end;
for i:=2 to n do
begin
for j:=1 to i-1 do
if f1[i]<f1[j] then begin f1[i]:=f1[j];x[i,1]:=j;end;
end;
for j:=2 to m do
begin
45
for i:=1 to n do
for k:=0 to i do
if f2[i]<f1[i-k]+a[k,j] then
begin
f2[i]:=f1[i-k]+a[k,j];
x[i,j]:=k;
end;
f1:=f2;
end;
end;
procedure xuat;
var i,j:word;
begin
assign(g,fo); rewrite(g);
writeln(g,f2[n]);
j:=m;
while (f2[n]>0) and (j>0) and (n>0) do
begin
a[1,j]:=x[n,j];
n:=n-x[n,j];
j:=j-1;
end;
for j:=1 to m do write(g,a[1,j],' ');
close(g);
end;
BEGIN doc;xl;xuat; END.
2. Cài đặt chi tiết của bài toán Du lịch vòng quanh thế giới:
{$M 63840,0,655360}
{$R+,Q+}
Const Fi = 'Tour.in1';
Fo = 'Tour.out';
Type Mg = Array[0..10000] Of Real;
Var N,p : Longint;
F : Text;
A : Array[0..10000] Of Longint;
Tr : Array[0..10000] Of Integer;
Qh : ^mg;
46
Procedure Init;
Var I : Integer;
Begin
New(qh);
Assign(f,fi); Reset(f); A[0]:=0;
Readln(f,n,p);
For i:=1 to n do Read(f,a[i]);
Close(f);
End;
Function Gt(k,j:Integer):real;
Begin
Gt:=(qh^[k]-qh^[j])/(a[k]-a[j])+a[k]+a[j];
End;
Procedure QHD;
Var I,j,d,c,ff,ql : Longint; Min,tong,ton : Real;
Q: Array[0..10000] Of Integer;
Begin
D:=1; C:=1; Q[1]:=0; Ql:=1;
Qh^[0]:=0.0; Tr[0]:=0;
For i:=1 to n do
Begin
Ff:=2*a[i]-2*p;
While (ql>1) and (gt(q[d],q[d+1])<=ff) do
Begin
Inc(d); Dec(ql);
End;
Ton:=p-(a[i]-a[q[d]]);
Qh^[i]:=Qh^[q[d]]+ton*ton;
Tr[i]:=Q[d];
While (ql>1) and (gt(q[c],i)<gt(q[c-1],q[c])) do
Begin
Dec(c); Dec(ql);
End;
Inc(c); Q[c]:=i; Inc(ql);
End;
End;
47
Procedure Lan_Nguoc;
Var Kq : Array[1..10000] Of Integer; Dem,i :
Integer;
Begin
Assign(f,fo); Rewrite(f);
Writeln(f,qh^[n]:0:0);
Dem:=0; I:=n;
Repeat
Inc(dem); Kq[dem]:=i; I:=tr[i];
Until i=0;
Writeln(f,dem);
For i:=dem downto 1 do Write(f,kq[i],' ');
Close(f);
Dispose(qh);
End;
BEGIN
Init; QHD; Lan_nguoc;
END.
48
MỤC LỤC
Trang
Phần 1: Hướng dẫn sử dụng phần mềm Adobe Connect 1
1. Các tính năng chính 1
2. Ứng dụng của Web Conference 1
3. Điều kiện sử dụng 2
4. Các quyền sử dụng 2
5. Đăng nhập với người sử dụng 3
6. Màn hình đầu tiên 3
7. Lựa chọn và điều chỉnh âm thanh 4
8. Khắc phục hiệ tượng rú rít vaà tiếng vọng 5
9. Đàm thoại 6
10. Chọn Video 6
11. Chọn Webcam 6
12. Chia sẻ màn hình 8
13. Điều chỉnh kích thước window và bố trí mặt bằng làm việc 9
14. Điều khiển P 10
15. Báo hiệu xin ý kiến 11
16. Thiết kế mặt bằng: Thêm bớt các cửa sổ nghiệp vụ 11
17. Ghi hình để phát lại 12
18. Sử dụng Adobe Connect với Adobe Presenter 12
Phần 2: Kết hợp kỹ thuật đánh dấu phần tử và xử lý bít để giải
quyết một số bài toán tron tin học
13
I. Một số vấn đề cơ bản về đánh dấu phần tử và xử lý bít. 14
1.1. Đánh dấu phần tử 14
1.2. Xử lý bít 14
II. Kết hợp kỹ thuật đánh dấu phần tử với xử lý bít để giải quyết
một số bài toán trong Tin học
17
2.1. Bài toán sắp xếp 17
2.2. Bài toán lọc dữ liệu 22
Phần 3: Kỹ thuật cải tiến khi giải quyết một bài toán trong tin học
bằng phương pháp quy hoạch động
28
I Kỹ thuật cải tiến trên không gia nhớ 28
1.1. Ví dụ 1 29
1.2. Ví dụ 2 31
1.3. Ví dụ 3 33
II. Kỹ thuật cải tiến trên thời gian thực hiện chương trình 37
2.1. Ví dụ 1 37
2.2. Ví dụ 2 40
File đính kèm:
 tai_lieu_boi_duong_thuong_xuyen_danh_cho_giao_vien_thpt_mon.pdf
tai_lieu_boi_duong_thuong_xuyen_danh_cho_giao_vien_thpt_mon.pdf

