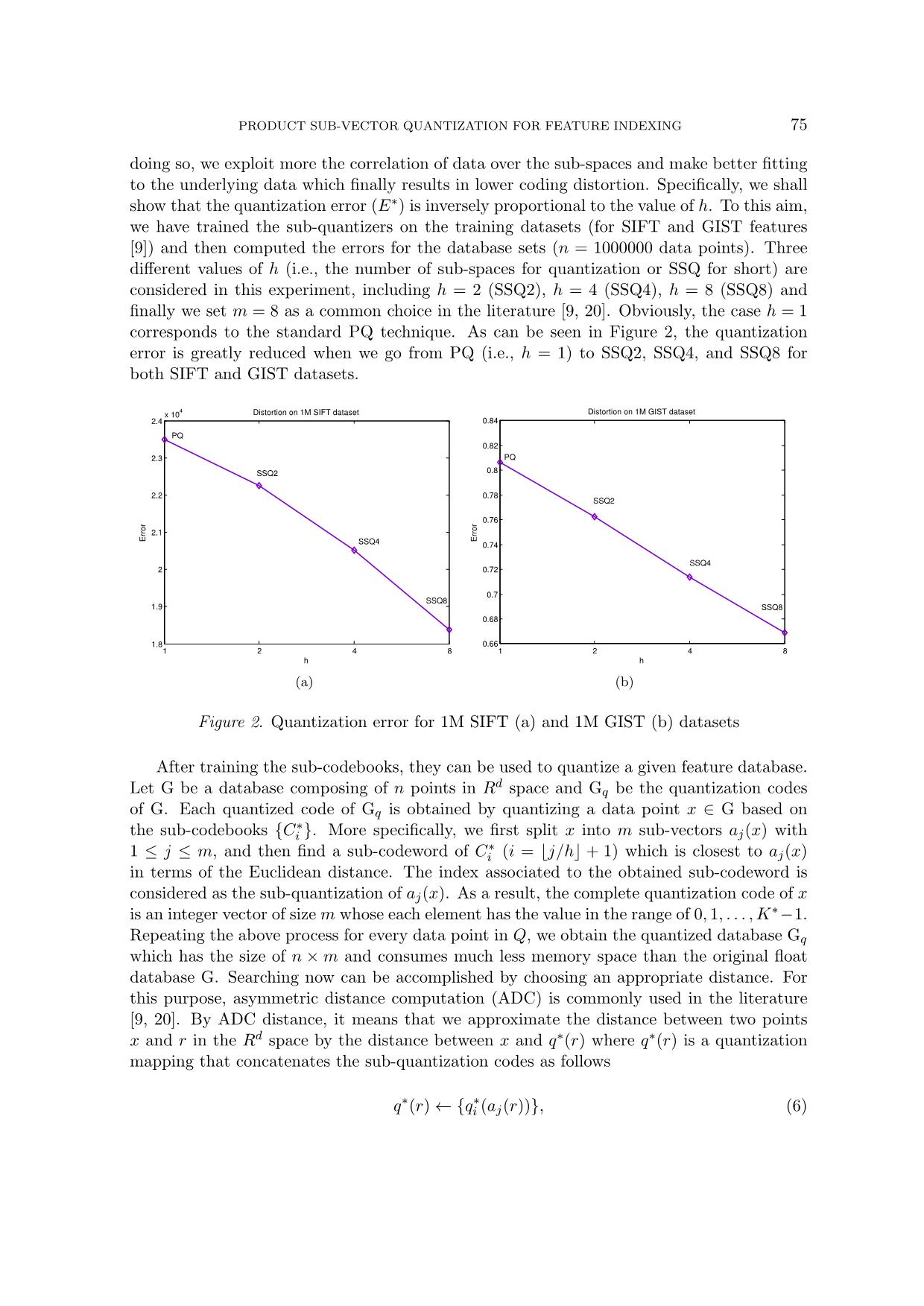
Product sub - vector quantization for feature indexing

proposed method with other PQ-based techniques that have particular
78 THE-ANH PHAM
interest in optimizing the quantizers. To this aim, we have selected the two representative
methods including the standard PQ and the ck-means method [20].
The second test compares the search efficiency or ANN search performance of the pro-
posed method. Because the main goal here is to investigate the indexing aspect, we have
thus selected the best indexing strategies including: IVFADC (i.e., PQ combined with an
inverted file structure using the ADC distance [9]), K-means tree [16] (i.e., the most efficient
technique for ANN search of FLANN library2), POC-tree [22], EPQ [25], and optimized
EPQ (OEPQ) [23]. The source codes are in C/C++ environment and the test is carried out
on a standard computer with following configuration: Windows 7, 16Gb RAM, Intel Core
(Dual-Core) i7 2.1 GHz.
As for the evaluation metrics, the first test employs Recall@R protocol, while the second
test uses speedup/precision curves. Those criteria are commonly used in the literature for the
same tasks [9, 17, 18, 20]. Specifically, Recall@R measures the faction of corrected answers
from a shortlist of R elements. The speedups are relatively computed over linear scan search
for avoiding the impact of computer configuration. To have a stable report, we have run
thousands of queries and then computed the mean results as the final output.
Two public datasets are used for all of our experiments. They include ANN SIFT1M and
ANN GIST1M [9]. Some basic information is reported in Table 1 for both the datasets. For
training the quantizers, PQ, ck-means, and the proposed method use the training set which
is different from the database and test sets. In addition, all these methods also use the same
parameter settings as follows: m = 8 and K = 256. Differently, the remaining methods
(i.e., K-means tree, POC-tree, EPQ and OEPQ) use directly the database for training the
quantizers (if any) and the clustering trees as well because they have been specifically targeted
to the indexing aspect.
Table 1. The datasets used in our experiments
Dataset #Training set #Database #Queries #Dimension
ANN SIFT1M 100,000 1,000,000 10,000 128
ANN GIST1M 500,000 1,000,000 1000 960
4.2. Evaluation of coding quality
We compare the proposed method against PQ and ck-means in terms of coding quality
for different sceneries of h as mentioned before, including SSQ2, SSQ4, and SSQ8 which
correspond to 4, 2, and 1 sub-quantizers, respectively. For instances, using h = 2 (SSQ2)
means that we group the data of two successive sub-spaces before applying the vector quan-
tization process and thus resulting in 4 sub-quantizers in total. To this aim, Algorithm 2 is
employed to compute the Recall@R scores of our algorithm. Figure 4 presents the results of
all the methods for both SIFT and GIST datasets. One can observe that SSQ2, SSQ4, and
SSQ8 perform consistently better than both PQ and ck-means for SIFT features. For GIST
dataset, ck-means is only outperformed by our SSQ8 variant probably due to the impact of
2
PRODUCT SUB-VECTOR QUANTIZATION FOR FEATURE INDEXING 79
highly dimensional effect. These results are quite impressive when considering that ck-means
has been fully optimized for capturing the intrinsic distribution of underlying data.
On the other hand, Figure 4 also shows that PQ when combined with the structured
order strategy for space decomposition is still not superior to our simplest model SSQ2.
Obviously, the SSQ8 variant performs best because the correlation of data is exploited at
maximum over all the sub-spaces, resulting in the lowest coding distortion as empirically
presented in Figure 2. However, this superior coding quality does not necessarily imply the
improvement in search efficiencies because of the computational overhead when computing
the distances. As a result, one has to make a trade-off between both these aspects depending
on specific application context.
100 101 102 103
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
R
R
ec
al
l@
R
1M SIFT (2048 codewords, asymmetric distance)
Ours−SSQ8
Ours−SSQ4
Ours−SSQ2
PQ
ck−means
(a)
100 101 102 103
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
R
R
ec
al
l@
R
1M GIST (2048 codewords, asymmetric distance)
Ours−SSQ8
Ours−SSQ4
Ours−SSQ2
PQ
ck−means
(b)
Figure 4. Coding quality for SIFT (a) and GIST (b) features
4.3. Evaluation of approximate nearest neighbor search
In this part, we investigate the efficiency of the proposed sub-quantizers for the task of
ANN search. To this aim, we employ the indexing strategy as presented by the authors
in [23]. This protocol is a standard pipeline composed of a clustering tree for hierarchical
representation of the whole database, and a heuristic engine for driving the search for a
given query. This indexing structure was coupled with the PQ-based quantizers and have
employed ADC distances to return an ordered list of candidate answers. To the best of our
understanding, this method currently yields the state-the-art results for ANN search on the
studied datasets. However, these results have been obtained with a constraint that the data
space for GIST features is divided into many small sub-spaces to avoid the problem of highly
dimensional effect.
Differing from the aforementioned work, the main goal of this study is to evaluate the
search efficiency when using even much simple settings (i.e., the data space is divided into 8
sub-spaces for both SIFT ad GIST features). As mentioned before, ANN search performance
is measured by the means of speedup/precision curves. Here, the search precision can be
considered as a special case of Recall@R where R = 1. That means the fraction of true
80 THE-ANH PHAM
answers when considering the short-list containing only one candidate. To obtain a wide
range of speedup/precision points, several parameters are varied when performing the query.
More detail is referred to original work [23].
Figure 5 compares the ANN search efficiencies of our method against recent works in-
cluding EPQ, OEPQ, POC-tree, and Kmeans-tree. As shown from Figure 5, the proposed
method performs on par with the state-of-the-art indexing techniques (i.e., OEPQ and EPQ)
for the SIFT features, and especially outperforms all other methods for GIST dataset. On
average, the proposed method is about 2.5× to 3.0× faster than the best algorithm of FLANN
library (i.e., Kmeans-tree). The gain in speedups is even higher for GIST features. Taking
a particular snapshot at the search precision of 85%, our algorithm is 500× and 365× fas-
ter than sequence search for GIST and SIFT, respectively. Obviously, one can even obtain
further interesting results by dividing the data space into more than 8 sub-spaces (m = 16
for example). However, we have not conducted this option in the present work.
80 82.5 85 87.5 90 92.5 95
100
150
200
250
300
400
500
Precision (%)
Sp
ee
du
p 
ov
er
 s
eq
ue
nc
e 
se
ar
ch
SIFT dataset (128D): 10K queries and 1M data points
Ours
OEPQ
EPQ
POC−tree
Kmeans−tree
(a)
80 82.5 85 87.5 90 92.5 95
50
100
200
300
400
500
600
700
Precision (%)
Sp
ee
du
p 
ov
er
 s
eq
ue
nc
e 
se
ar
ch
GIST dataset (960D): 1K queries and 1M data points
Ours
OEPQ
EPQ
POC−tree
Kmeans−tree
(b)
Figure 5. ANN search performance for SIFT (a) and GIST (b) features
Lastly, we also provide a short evaluation of our method with the IVFADC technique [9]
by comparing the search speedups relatively to the best algorithm of FLANN as suggested in
[23]. One advantage of this way is that one can avoid the barrier and subjective evaluation
caused by re-implementing the algorithm and parameter tuning. As reported by the authors
in [9] and [23], the speedup of IVFADC is about 1.5× to 2.0× higher than the best algorithm
of FLANN for the same precisions on SIFT dataset, while the proposed method, as noticed
before, is roughly 2.5× to 3.0× more efficient. The obtained results are quite impressive
which demonstrates the efficiency and effectiveness of the proposed quantizers although the
idea is conceptually simple.
5. CONCLUSIONS
The proposed method has been designed to exploit the correlation of underlying data by
allowing a centroid to be associated to more than one sub-space. Hence, the density of each
cluster is higher when comparing to individual quantizer created separately in each sub-space.
PRODUCT SUB-VECTOR QUANTIZATION FOR FEATURE INDEXING 81
In addition, the proposed method also takes into consideration the prior knowledge of data
distribution to decide the appropriate space splitting action. The resulting quantizers have
nice properties in that they yield lower coding errors, create finer data representation, and
consume same bit budget for storing the sub-codewords as standard PQ methods do. Various
experiments have been conducted which showed the superior performance of the proposed
method in comparison with other techniques. For extension of this work, we intend to study
the incorporation of deep learning approach for boosting the search performance.
ACKNOWLEDGMENT
This research is funded by Vietnam National Foundation for Science and Technology
Development (NAFOSTED) under grant number 102.01-2016.01.
REFERENCES
[1] A. Babenko and V. Lempitsky, “Additive quantization for extreme vector compression,” in 2014
IEEE Conference on Computer Vision and Pattern Recognition, 2014, pp. 931–938.
[2] ——, “The inverted multi-index,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 37, no. 6, pp.
1247–1260, 2015.
[3] ——, “Tree quantization for large-scale similarity search and classification,” in 2015 IEEE Con-
ference on Computer Vision and Pattern Recognition (CVPR), 2015, pp. 4240–4248.
[4] M. Ester, H.-P. Kriegel, J. Sander, and X. Xu, “A density-based algorithm for discovering
clusters a density-based algorithm for discovering clusters in large spatial databases with noise,”
in Proceedings of the Second International Conference on Knowledge Discovery and Data Mining,
ser. KDD’96. AAAI Press, 1996, pp. 226–231.
[5] J. H. Friedman, J. L. Bentley, and R. A. Finkel, “An algorithm for finding best matches in
logarithmic expected time,” ACM Trans. Math. Softw., vol. 3, no. 3, pp. 209–226, 1977.
[6] T. Ge, K. He, Q. Ke, and J. Sun, “Optimized product quantization,” IEEE Trans. Pattern Anal.
Mach. Intell., vol. 36, no. 4, pp. 744–755, 2014.
[7] R. M. Gray and D. L. Neuhoff, “Quantization,” IEEE Transactions on Information Theory,
vol. 44, no. 6, pp. 2325–2383, 1998.
[8] P. Indyk and R. Motwani, “Approximate nearest neighbors: towards removing the curse of di-
mensionality,” in Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computing,
ser. STOC’98, 1998, pp. 604–613.
[9] H. Jegou, M. Douze, and C. Schmid, “Product quantization for nearest neighbor search,” IEEE
Trans. Pattern Anal. Mach. Intell., vol. 33, no. 1, pp. 117–128, 2011.
[10] Y. Kalantidis and Y. Avrithis, “Locally optimized product quantization for approximate nearest
neighbor search,” in Proceedings of International Conference on Computer Vision and Pattern
Recognition (CVPR 2014), Columbus, Ohio, June 2014, pp. 2329–2336.
[11] L. Kaufman and P. J. Rousseeuw, “Clustering by means of medoids,” pp. 405–416, 1987.
[12] B. Kulis and K. Grauman, “Kernelized locality-sensitive hashing for scalable image search,” in
IEEE International Conference on Computer Vision, ser. ICCV’09, 2009, pp. 2130–2137.
82 THE-ANH PHAM
[13] L. Li, Q. Hu, Y. Han, and X. Li, “Distribution sensitive product quanti-
zation,” IEEE Transactions on Circuits and Systems for Video Technology.
https://doi.org/10.1109/TCSVT.2017.2759277, 2017.
[14] D. G. Lowe, “Distinctive image features from scale-invariant keypoints,” International Journal
of Computer Vision, vol. 60, no. 2, pp. 91–110, 2004.
[15] J. B. Macqueen, “Some methods for classification and analysis of multivariate observations,” in
In 5-th Berkeley Symposium on Mathematical Statistics and Probability, 1967, pp. 281–297.
[16] M. Muja and D. G. Lowe, “Fast approximate nearest neighbors with automatic algorithm con-
figuration,” in Proceedings of International Conference on Computer Vision Theory and Appli-
cations, ser. VISAPP’09, 2009, pp. 331–340.
[17] ——, “Fast matching of binary features,” in Proceedings of the Ninth Conference on Computer
and Robot Vision, ser. CRV’12, 2012, pp. 404–410.
[18] ——, “Scalable nearest neighbor algorithms for high dimensional data,” IEEE Transactions on
Pattern Analysis and Machine Intelligence, vol. 36, pp. 2227–2240, 2014.
[19] D. Nister and H. Stewenius, “Scalable recognition with a vocabulary tree,” in Proceedings of
the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition -
Volume 2, ser. CVPR’06, 2006, pp. 2161–2168.
[20] M. Norouzi and D. J. Fleet, “Cartesian k-means,” in Proceedings of the 2013 IEEE Conference
on Computer Vision and Pattern Recognition, ser. CVPR ’13, 2013, pp. 3017–3024.
[21] A. Oliva and A. Torralba, “Modeling the shape of the scene: A holistic representation of the
spatial envelope,” Int. J. Comput. Vision, vol. 42, no. 3, pp. 145–175, 2001.
[22] T.-A. Pham, “Pair-wisely optimized clustering tree for feature indexing,” Computer Vision and
Image Understanding, vol. 154, no. 1, pp. 35–47, 2017.
[23] ——, “Improved embedding product quantization,” Machine Vision and Applications, Published
online 13 Feb 2019. https://doi.org/10.1007/s00138-018-00999-2, 2018.
[24] T.-A. Pham, S. Barrat, M. Delalandre, and J.-Y. Ramel, “An efficient indexing scheme based
on linked-node m-ary tree structure,” in 17th International Conference on Image Analysis and
Processing (ICIAP 2013), ser. LNCS, vol. 8156, 2013, pp. 752–762.
[25] T.-A. Pham and N.-T. Do, “Embedding hierarchical clustering in product quantization for fea-
ture indexing,” Multimedia Tools and Applications. https://doi.org/10.1007/s11042-018-6626-9,
2018.
[26] C. Silpa-Anan and R. Hartley, “Optimised kd-trees for fast image descriptor matching,” in IEEE
Conference on Computer Vision and Pattern Recognition, ser. CVPR’08, 2008, pp. 1–8.
[27] J. Willamowski, D. Arregui, G. Csurka, C. R. Dance, and L. Fan, “Categorizing nine visual
classes using local appearance descriptors,” in In ICPR Workshop on Learning for Adaptable
Visual Systems, 2004.
[28] T. Zhang, C. Du, and J. Wang, “Composite quantization for approximate nearest neighbor
search,” in Proceedings of the 31st International Conference on Machine Learning (ICML-14),
2014, pp. 838–846.
PRODUCT SUB-VECTOR QUANTIZATION FOR FEATURE INDEXING 83
[29] T. Zhang, G.-J. Qi, J. Tang, and J. Wang, “Sparse composite quantization,” in Proceedings of
International Conference on Computer Vision and Pattern Recognition (CVPR’15), 2015, pp.
4548–4556.
Received on December 14, 2018
Revised on March 10, 2019