Phân loại dấu vân tay với rừng ngẫu nhiên xiên phân và phương pháp biểu diễn đặc trưng không đổi

h sẽ được gán vào cluster gần nhất. Đếm số lượng các véctơ được gán vào các từ 
Tạp chí Khoa học 2010:15a 253-262 Trường Đại học Cần Thơ 
 257 
trực quan tương ứng, ta thu được một véctơ tần xuất mô tả sự xuất hiện của các từ 
trực quan trên ảnh. Ảnh sẽ được biểu diễn bằng véctơ tần suất này. 
3 RỪNG NGẪU NHIÊN XIÊN PHÂN 
Bước tiền xử lý ảnh vân tay sẽ tạo ra tập dữ liệu có số chiều rất lớn (hơn 1000 
chiều). Giải thuật phân lớp được chọn tiếp theo phải có khả năng xử lý tốt dữ liệu 
có số chiều lớn. Một nghiên cứu trước đây trong [6], chúng tôi đã đề nghị dùng 
giải thuật rừng ngẫu nhiên xiên phân (RF-ODT) được biết đến như là một giải 
thuật hiệu quả cho việc phân lớp dữ liệu có số chiều lớn. Đây là sự mở rộng từ RF-
CART được đề nghị bởi Breiman [3]. Giải thuật RF-CART được phát triển trên ý 
tưởng của Bagging [2], phương pháp tiếp cận không gian con ngẫu nhiên của 
[1, 10]. Tiếp cận Bagging của Breiman, tập hợp các cây quyết định [4, 19] được 
xây dựng từ việc lấy mẫu dùng bootstrap – lấy mẫu có hoàn lại từ tập dữ liệu ban 
đầu. Sau đó kết hợp kết quả dự đoán của các cây, bầu chọn số đông cho vấn đề 
phân loại. Ho [10] cũng đưa ra phương pháp không gian con ngẫu nhiên – trong đó 
chọn ngẫu nhiên một tập con của các thuộc tính để phát triển mỗi cây. Amit và 
Geman [1] dùng việc chọn ngẫu nhiên các thuộc tính để tìm kiếm phân hoạch tốt 
nhất tại mỗi nút. Cuối cùng, các tiếp cận này được mở rộng và chính thức được 
dùng trong rừng ngẫu nhiên của Breiman [3]. Giải thuật RF-CART của Breiman 
xây dựng một tập hợp các cây quyết định hiệu quả cao nhưng có sự tương quan 
thấp giữa các cây thành viên. Breiman đã đề nghị dùng hai chiến lược để giữ bias 
thấp (sai lệch thấp) và sự phụ thuộc giữa các cây trong rừng thấp. Để đạt được sai 
lệch thấp, ông đề nghị xây dựng các cây đến độ sâu tối đa không cần cắt nhánh. Để 
giữ tính tương quan giữa các cây ở mức thấp, ông đề nghị sử dụng việc lấy mẫu có 
hoàn lại (bootstrap) từ tập dữ liệu ban đầu để xây dựng cây thành viên và chọn 
ngẫu nhiên một tập con các thuộc tính để tính phân hoạch tốt nhất ở các nút trong 
của cây. Xét một tác vụ phân loại với m phần tử dữ liệu xi (i = 1,m) và n chiều 
(thuộc tính), một cây quyết định (ký hiệu là DT) trong rừng ngẫu nhiên gồm k cây 
(ký hiệu RF = {DTi}i=1,k) được xây dựng như sau : 
- Tập dữ liệu học là m phần tử dữ liệu được lấy mẫu có hoàn lại (kiểu bootstrap) 
từ tập dữ liệu ban đầu. 
- Tại mỗi nút của cây, chọn ngẫu nhiên n’ chiều (n’<<n) và tính toán phân hoạch 
(chỉ số Gini [4]) tốt nhất dựa trên n’ chiều này. 
- Cây được xây dựng đến độ sâu tối đa không cắt nhánh. 
Rừng ngẫu nhiên RF-CART cho độ chính xác cao so với các giải thuật phân lớp 
tốt nhất hiện nay bao gồm Boosting [8] và SVM [21]. Hơn nữa, thời gian huấn 
luyện của RF-CART nhanh, mô hình chịu đựng nhiễu tốt và không bị “học vẹt”. 
Tuy nhiên, việc xây dựng cây thành viên trong RF-CART chỉ chọn một chiều để 
phân hoạch dữ liệu tại các nút như đề nghị trước đây [1, 4, 19]. Do đó, tính mạnh 
mẽ của cây bị giảm khi làm việc với các tập dữ liệu có số chiều lớn và phụ thuộc 
lẫn nhau. Ví dụ như trong hình 4, bất kỳ việc phân hoạch đơn thuộc tính nào (song 
song với trục tọa độ) đều không thể tách dữ liệu một lần duy nhất thành hai lớp 
một cách hoàn toàn mà phải thực hiện nhiều lần phân hoạch, nhưng việc phân 
hoạch đa chiều (xiên phân, kết hợp hai thuộc tính) có thể thực hiện một cách hoàn 
Tạp chí Khoa học 2010:15a 253-262 Trường Đại học Cần Thơ 
 258 
hảo với duy nhất một lần. Vì thế, việc phân hoạch đơn thuộc tính được dùng để 
xây dựng cây thông thường thì không hiệu quả trong trường hợp này. 
Hình 4: Phân hoạch đơn thuộc tính (trái), phân hoạch đa thuộc tính (phải) 
Để khắc phục nhược điểm trên, nhiều giải thuật xây dựng cây quyết định sử dụng 
phân hoạch đa thuộc tính (xiên phân) tại các nút được đề nghị. Vấn đề xây dựng 
cây quyết định xiên tối ưu đã được biết như là một vấn đề có độ phức tạp NP-hard. 
Nghiên cứu tiên phong của Murthy và các cộng sự trong [17] đã đưa ra giải thuật 
OC1, một hệ thống dùng để xây dựng các cây quyết định xiên trong đó dùng thuật 
toán leo đồi (Hill-climbing) để tìm một phân hoạch xiên tốt dưới dạng một 
siêu phẳng. 
Rừng ngẫu nhiên xiên phân RF-ODT của chúng tôi trong [6] xây dựng các cây 
xiên phân ngẫu nhiên dựa trên siêu phẳng tối ưu (phân hoạch hiệu quả cao, khả 
năng chịu đựng nhiễu tốt) thu được từ huấn luyện SVM [21]. Việc tìm siêu phẳng 
tối ưu của SVM được làm như sau. 
Hình 5: Phân lớp tuyến tính với máy học véctơ hỗ trợ 
Xét ví dụ phân lớp nhị phân tuyến tính như hình 5. SVM tìm siêu phẳng tối ưu 
(xác định bởi véctơ pháp tuyến w và độ lệch của siêu phẳng b) dựa trên 2 siêu 
phẳng hỗ trợ của 2 lớp. Các phần tử lớp +1 nằm bên phải của siêu phẳng hỗ trợ 
cho lớp +1, các phần tử lớp -1 nằm phía bên trái của siêu phẳng hỗ trợ cho lớp -1. 
Những phần tử nằm ngược phía với siêu phẳng hỗ trợ được coi như lỗi. Khoảng 
cách giữa 2 siêu phẳng hỗ trợ được gọi là lề. Mô hình phân hoạch tốt (siêu phẳng 
tối ưu nằm giữa 2 siêu phẳng hỗ trợ) tìm được từ 2 tiêu chí là cực đại hóa lề (lề 
càng lớn, mô hình phân lớp càng an toàn) và cực tiểu hóa lỗi. Vấn đề dẫn đến việc 
giải bài toán quy hoạch toàn phương được biết phổ biến trong toán tối ưu hóa. 
SVM có thể sử dụng hàm nhân để phân lớp phi tuyến tính. Đọc giả quan tâm có 
thể tham khảo thêm từ sách [21]. 
Tạp chí Khoa học 2010:15a 253-262 Trường Đại học Cần Thơ 
 259 
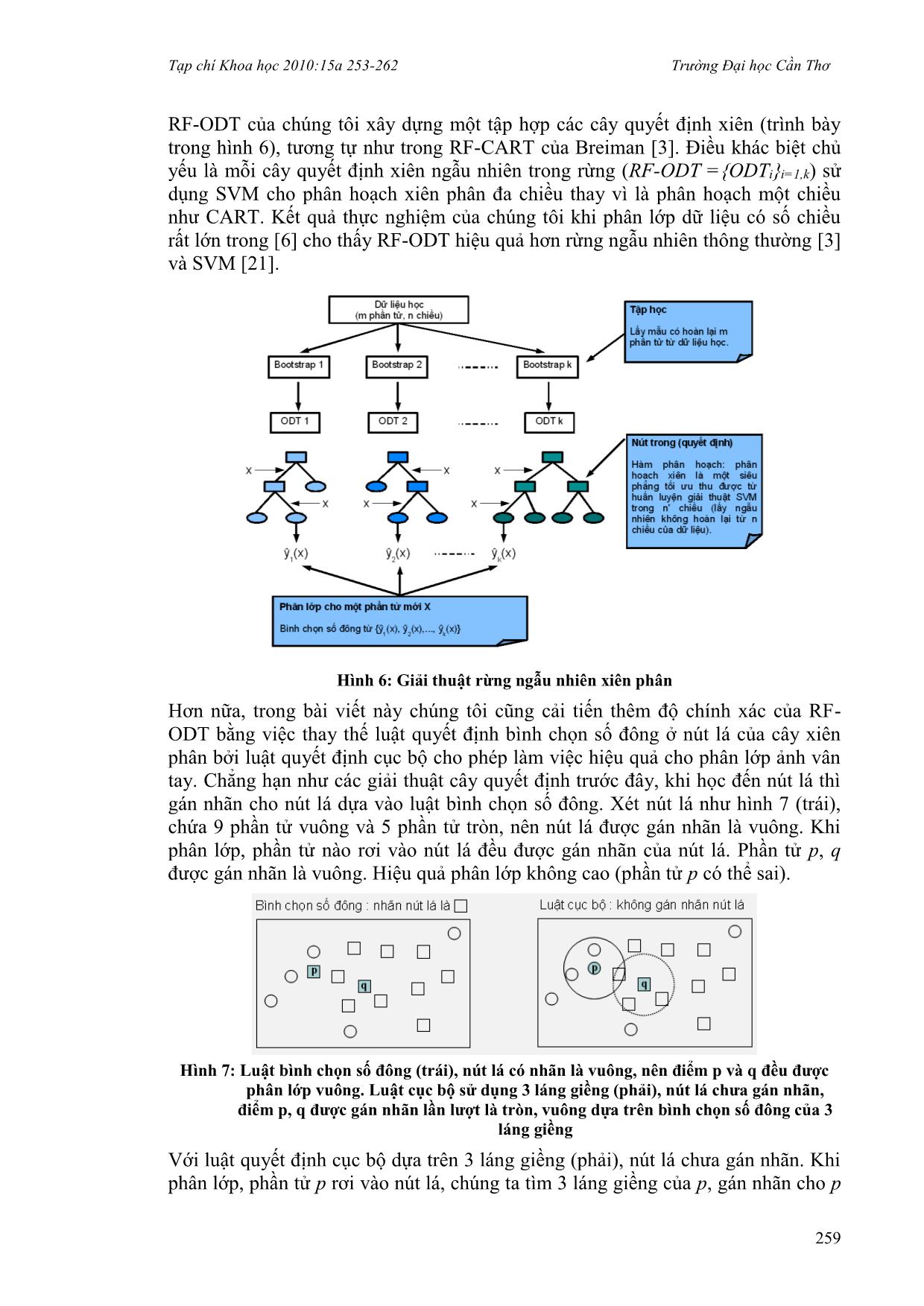
RF-ODT của chúng tôi xây dựng một tập hợp các cây quyết định xiên (trình bày 
trong hình 6), tương tự như trong RF-CART của Breiman [3]. Điều khác biệt chủ 
yếu là mỗi cây quyết định xiên ngẫu nhiên trong rừng (RF-ODT ={ODTi}i=1,k) sử 
dụng SVM cho phân hoạch xiên phân đa chiều thay vì là phân hoạch một chiều 
như CART. Kết quả thực nghiệm của chúng tôi khi phân lớp dữ liệu có số chiều 
rất lớn trong [6] cho thấy RF-ODT hiệu quả hơn rừng ngẫu nhiên thông thường [3] 
và SVM [21]. 
Hình 6: Giải thuật rừng ngẫu nhiên xiên phân 
Hơn nữa, trong bài viết này chúng tôi cũng cải tiến thêm độ chính xác của RF-
ODT bằng việc thay thế luật quyết định bình chọn số đông ở nút lá của cây xiên 
phân bởi luật quyết định cục bộ cho phép làm việc hiệu quả cho phân lớp ảnh vân 
tay. Chẳng hạn như các giải thuật cây quyết định trước đây, khi học đến nút lá thì 
gán nhãn cho nút lá dựa vào luật bình chọn số đông. Xét nút lá như hình 7 (trái), 
chứa 9 phần tử vuông và 5 phần tử tròn, nên nút lá được gán nhãn là vuông. Khi 
phân lớp, phần tử nào rơi vào nút lá đều được gán nhãn của nút lá. Phần tử p, q 
được gán nhãn là vuông. Hiệu quả phân lớp không cao (phần tử p có thể sai). 
Hình 7: Luật bình chọn số đông (trái), nút lá có nhãn là vuông, nên điểm p và q đều được 
phân lớp vuông. Luật cục bộ sử dụng 3 láng giềng (phải), nút lá chưa gán nhãn, 
điểm p, q được gán nhãn lần lượt là tròn, vuông dựa trên bình chọn số đông của 3 
láng giềng 
Với luật quyết định cục bộ dựa trên 3 láng giềng (phải), nút lá chưa gán nhãn. Khi 
phân lớp, phần tử p rơi vào nút lá, chúng ta tìm 3 láng giềng của p, gán nhãn cho p 
Tạp chí Khoa học 2010:15a 253-262 Trường Đại học Cần Thơ 
 260 
dựa trên bình chọn số đông từ 3 láng giềng, nhãn của p được gán là tròn. Tương tự, 
phần tử q được gán nhãn là vuông từ bình chọn số đông từ 3 láng giềng của nó. 
Với việc thay thế luật quyết định này, RF-ODT cho độ chính xác cao khi phân lớp 
ảnh vân tay. 
4 KẾT QUẢ THỰC NGHIỆM 
Chúng tôi rất quan tâm đến độ chính xác của hệ thống phân loại vân tay đề nghị 
trong nghiên cứu. Do đó chúng tôi đã tiến hành thử nghiệm trên dữ liệu thực tế để 
đánh giá hiệu quả của phương pháp đề nghị. Chúng tôi đã thu thập 480 ảnh dấu 
vân tay (như được mô tả trong bảng 1) của 15 đồng nghiệp bằng thiết bị đọc 
Microsoft ® Fingerprint và bộ công cụ libfprint [7]. Sau đó, chúng tôi cũng sử 
dụng thư viện [16] để tiền xử lý ảnh, rút trích các điểm đặc trưng từ giải thuật phát 
hiện Hessian Affine và véctơ mô tả SIFT. Sau đó, giải thuật k-means [15] được áp 
dụng để gom nhóm các véctơ mô tả SIFT vào 2000 clusters tương ứng với 2000 từ 
vựng. Tập dữ liệu bao gồm 480 véctơ trong 2000 chiều với 15 lớp tương ứng với 
15 cá nhân. Nghi thức kiểm tra chéo (10-fold) được áp dụng để đánh giá hiệu quả 
của các giải thuật phân lớp. Cách làm như sau: tập dữ liệu chia thành 10 phần bằng 
nhau, ở lần thứ i lấy ra phần thứ i để làm tập kiểm tra và 9 phần còn lại dùng làm 
tập huấn luyện. Kết quả được tổng hợp từ 10 lần thực thi như vừa mô tả. 
Bảng 1: Dữ liệu ảnh vân tay 
STT Cá nhân Số ảnh STT Cá nhân Số ảnh 
1 Nghi Do 85 9 Nha Le 23 
2 Kanh Le 28 10 Luan Nguyen 20 
3 Mien Nguyen 28 11 Lam Le 26 
4 Lieu Nguyen 32 12 Cang Phan 25 
5 Nguyen Lam 39 13 Hung Ngo 20 
6 Huyen Le 37 14 Huy Nguyen 21 
7 Binh Nguyen 39 15 Tuan Dang 30 
8 Ngu Tran 27 Tổng cộng: 480 
Chúng tôi muốn so sánh hiệu quả của giải thuật RF-ODT mà chúng tôi đề nghị với 
các giải thuật khác, bao gồm cây quyết định C4.5 [19], RF-CART [3], AdaBoost 
[8] của C4.5, SVM [21] và k láng giềng (kNN). Để thực hiện mục tiêu này, chúng 
tôi đã cài đặt giải thuật RF-ODT của chúng tôi bằng ngôn ngữ C/C++. Các giải 
thuật khác đã có trong các thư viện phần mềm miễn phí, như LibSVM [5], thư viện 
Weka [22] có sẵn các giải thuật C4.5, RF-CART, AdaBoost-C4.5 và kNN. Mỗi 
giải thuật đều có các tham số được chọn cho kết quả cao nhất. Cuối cùng chúng tôi 
thu được kết quả phân lớp của các giải thuật như bảng 2. 
Khi so sánh, chúng ta có thể thấy RF-ODT cho kết quả cao nhất với độ chính xác 
là 99,79%. LibSVM với hàm nhân RBF cũng cho kết quả 99,38% gần bằng RF-
ODT. Hai giải thuật tiếp theo là RF-CART và AdaBoost-C4.5 cho kết quả khá tốt. 
Tuy nhiên, kNN và C4.5 lại cho kết quả thấp cách biệt so với RF-ODT. 
Tạp chí Khoa học 2010:15a 253-262 Trường Đại học Cần Thơ 
 261 
Bảng 2: Kết quả phân lớp ảnh vân tay 
Tham số Giải thuật Chính xác (%) 
 50 cây, 100 chiều ngẫu nhiên, nút lá nhỏ nhất là 20, 
3 láng giềng cho gán nhãn 
 RF-ODT 99,79 
 gamma = 0,00015 cho hàm nhân RBF và hằng số 
cost = 1000 
 LibSVM 99,38 
 50 cây, 200 chiều ngẫu nhiên, nút lá nhỏ nhất là 2 RF-CART 98,75 
 50 cây, nút lá nhỏ nhất là 2 AdaBoost-C4.5 98,33 
 nút lá nhỏ nhất là 2 có cắt nhánh C4.5 91,04 
 5 láng giềng kNN 92,29 
Để xét chi tiết kết quả thu được từ RF-ODT, chúng tôi trình bày kết quả trong ma 
trận confusion mà ở đó dòng trình bày cho cá thể trong tập dữ liệu và cột là kết quả 
phân lớp của RF-ODT. Trong hình 8, ta có thể thấy rằng RF-ODT chỉ có sai duy 
nhất 1 ảnh vân tay của Binh Nguyen (lớp 7) được dự đoán vào Nghi Do (lớp 1). 
Tất cả 479 ảnh còn lại đều phân lớp đúng, đạt độ chính xác 99,79%. Chúng tôi tin 
tưởng rằng, hệ thống phân lớp vân tay dựa vào véctơ SIFT và RF-ODT có thể áp 
dụng vào thực tiễn. 
Hình 8: Kết quả phân lớp của rừng ngẫu nhiên xiên phân 
5 KẾT LUẬN VÀ HƯỚNG PHÁT TRIỂN 
Chúng tôi trình bày một hệ thống phân loại vân tay mới và hiệu quả. Ý tưởng 
chính xuất phát từ một mô hình trong phân tích văn bản: mô hình túi từ. Để áp 
dụng mô hình này lên ảnh, chúng tôi cho sử dụng các từ trực quan và mô hình hóa 
ảnh như túi các từ trực quan. Các từ trực quan được xây dựng bằng cách phân 
nhóm các đặc trưng cục bộ SIFT bằng giải thuật k-means. Theo mô hình này ảnh 
vân tay được biểu diễn bằng một véctơ tần suất mô tả phân phối của các từ trực 
quan trên ảnh. Trong giai đoạn phân lớp, chúng tôi đề xuất sử dụng và mở rộng 
giải thuật rừng ngẫu nhiên xiên phân. Các thử nghiệm được thực hiện trên 480 
Tạp chí Khoa học 2010:15a 253-262 Trường Đại học Cần Thơ 
 262 
hình ảnh dấu vân tay từ 15 đồng nghiệp của chúng tôi tại Khoa Công nghệ Thông 
tin & Truyền thông, trường Đại học Cần Thơ. Hệ thống phân loại vân tay của 
chúng tôi đã đạt được độ chính xác 99,79% (chỉ nhận dạng sai 1 ảnh). 
Với các kết quả khả quan thu được, chúng tôi dự định triển khai phương pháp này 
vào các ứng dụng thực tế như: chấm công tự động, nhận dạng tội phạm. Chúng tôi 
cũng sẽ tiến hành nhiều thử nghiệm nữa trên một số lượng dữ liệu lớn và cũng có 
thể so sánh với các phương pháp tiếp cận khác [7, 9] trong tương lai. 
TÀI LIỆU THAM KHẢO 
[1] Y. Amit and D. Geman. Shape quantization and recognition with randomized trees. Neural 
Computation (9):1545-1588, 1996. 
[2] L. Breiman. Bagging predictors. Machine Learning 24(2):123–140, 1996. 
[3] L. Breiman. Random forests. Machine Learning 45(1):5–32, 2001. 
[4] L. Breiman, J. Friedman, R. Olshen and C. Stone. Classification and Regression Trees. 
Wadsworth International, 1984. 
[5] C-C. Chang and C-J. Lin. LibSVM - a library for support vector machines. 2001. 
[6] T-N. Do, S. Lallich, N-K. Pham and P. Lenca. Classifying very-high-dimensional data with 
random forests of oblique decision trees. (to appear) in Advances in Knowledge Discovery 
and Management, H. Briand, F. Guillet, G. Ritschard, D. Zighed Eds, Springer-Verlag, 2009. 
[7] D. Drake. Libfprint. 2007. 
[8] Y. Freund and R. Schapire. A decision-theoretic generalization of on-line learning and an 
application to boosting. Computational Learning Theory, 1995, pp. 23–37. 
[9] Griaule Biometrics. Fingerprint SDK. 2007. 
[10] T-K. Ho. Random decision forest. In: Proceedings of the Third International Conference on 
Document Analysis and Recognition, 1995, pp. 278–282. 
[11] A. Jain and S. Pankanti. Fingerprint Classification and Matching. in Handbook for Image and 
Video Processing, A. Bovik (eds.), Academic Press, 2000. 
[12] D-G. Lowe. Object Recognition from Local Scale Invariant Features. in Proceedings of the 
7th International Conference on Computer Vision, Kerkyra, Greece, 1999, pp. 1150–1157. 
[13] D-G. Lowe. Distinctive Image Features from Scale Invariant Keypoints. in International 
Journal of Computer Vision, 2004, pp. 91–110. 
[14] D. Maltoni, D. Maio, A-K. Jain and S. Prabhakar. Handbook of Fingerprint Recognition. 
Springer, 2003. 
[15] J. MacQueen. Some methods for classification and analysis of multivariate observations. in 
Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability, 
Berkeley, University of California Press, (1):281-297, 1967. 
[16] K. Mikolajczyk and C. Schmid. Scale and Affine Invariant Interest Point Detectors. 
Proceedings of IJCV, vol. 60, no. 1, pp. 63–86, 2004. 
[17] S. Murthy, S. Kasif, S. Salzberg and R. Beigel. Oc1: Randomized induction of oblique 
decision trees. Proc. of the 11th National Conference on AI, 1993, pp. 322–327. 
[18] NSTC Subcommittee on Biometrics. Fingerprint Recognition. 2007. 
[19] J. Quinlan. C4.5: Programs for Machine Learning. Morgan Kaufmann, 1993. 
[20] C. Schmid and R Mohr. Local gray value invariants for image retrieval. IEEE Transactions 
on Pattern Analysis and Machine Intelligence, 19(5): 530–535, 1997. 
[21] V. Vapnik. The Nature of Statistical Learning Theory. Springer-Verlag, 1995. 
[22] I.H. Witten and E. Frank. Data Mining: Practical Machine Learning Tools and Techniques. 
Morgan Kaufmann, 2005.