On the performance of 1-Bit ADC in Massive MIMO communication systems

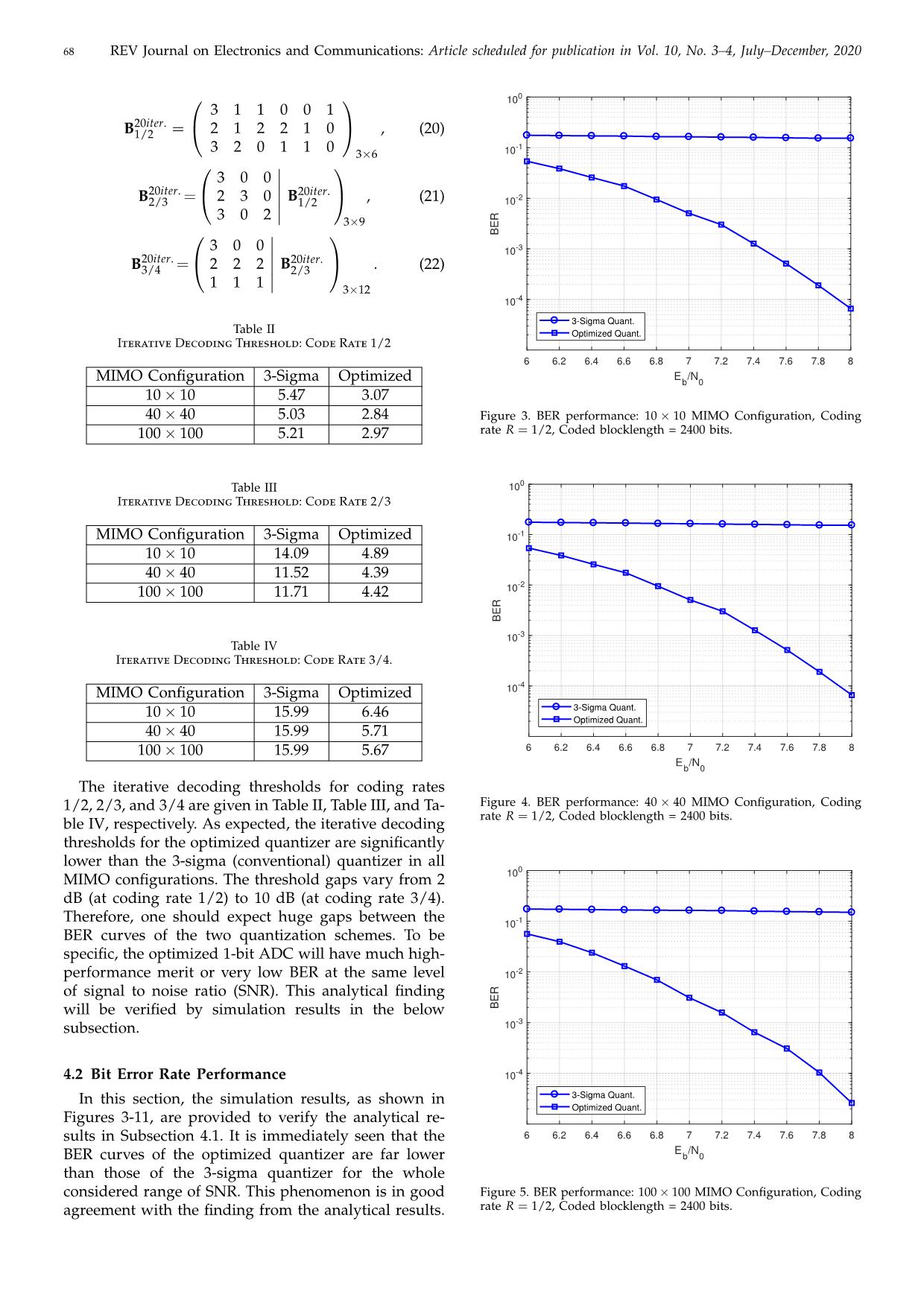
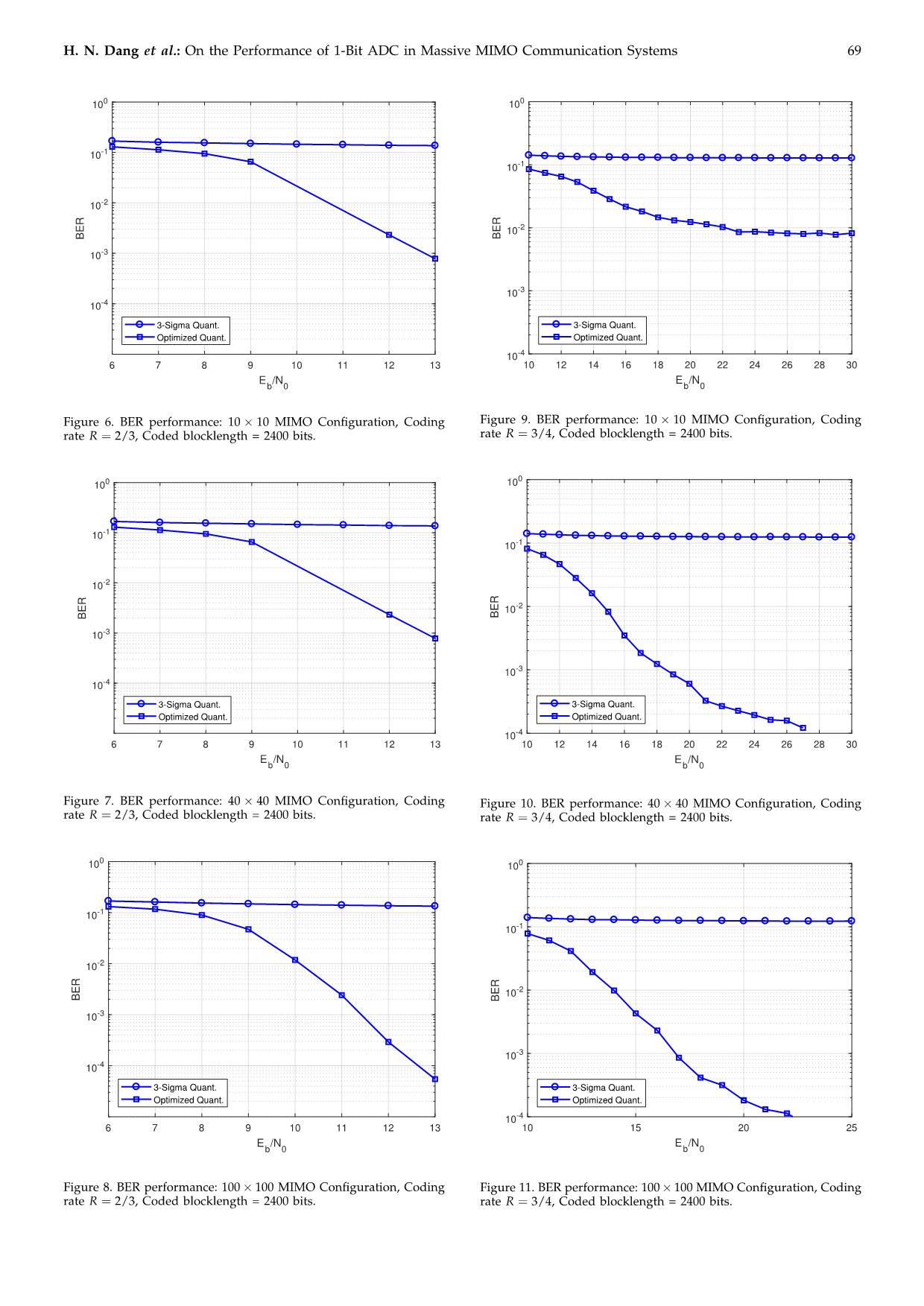
ected to the
 c posed in [12, 16], to evaluate the performance im-
m-th variable node, and N (m) is the set of observation
 o provement of the optimized 1-bit uniform quantizer.
nodes connected to the m-th variable node.
 Since utilizing the LS-MIMO PEXIT for 1-bit ADCs is
 3.2.3 Message Passed From Check Nodes to Variable straightforward, readers refer to those two references
Nodes: The message from the k-th check node to the for more details.
m-th variable node is identical to the conventional The LS-MIMO-PEXIT was proved to be a useful tool
message-passing algorithm [24] and given by for evaluating and designing protograph LDPC codes
 1 − ea[t,k] through the iterative decoding threshold. This is the
 1 −
 ∏ a[t,k] lowest received signal-to-noise ratio that the decoder
 t∈N (k)\m 1 + e
 b[k, m] = ln v , (16) can decode the noisy bitstream. Thus, the lower the iter-
 1 − ea[t,k] ative decoding threshold, the better the communication
 1 +
 ∏ a[t,k] systems can achieve.
 t∈N (k)\m 1 + e
 v To calculate the iterative decoding threshold, we se-
where Nv(k) is the set of variable nodes connected to lect the protograph LDPC codes that were previously
the k-th check node. In practical implementation, the optimized for LS-MIMO channels and joint double-
computation of b[k, m] is simplified by using the tanh(·) layer belief propagation receiver [16]. The selected pro-
function. tograph LDPC codes are given in (20), (21), (22).
68 REV Journal on Electronics and Communications: Article scheduled for publication in Vol. 10, No. 3–4, July–December, 2020
 100
  3 1 1 0 0 1 
 20iter.
 B1/2 =  2 1 2 2 1 0  , (20)
 -1
 3 2 0 1 1 0 3×6 10
  3 0 0 
 20iter. 20iter.
 B2/3 =  2 3 0 B1/2  , (21) 10-2
 3 0 2 3×9
   BER
 3 0 0 10-3
 20iter. 20iter.
 B3/4 =  2 2 2 B2/3  . (22)
 1 1 1 3×12
 10-4
 3-Sigma Quant.
 Table II Optimized Quant.
 Iterative Decoding Threshold:Code Rate 1/2
 6 6.2 6.4 6.6 6.8 7 7.2 7.4 7.6 7.8 8
 E /N
 MIMO Configuration 3-Sigma Optimized b 0
 10 × 10 5.47 3.07
 40 × 40 5.03 2.84 Figure 3. BER performance: 10 × 10 MIMO Configuration, Coding
 100 × 100 5.21 2.97 rate R = 1/2, Coded blocklength = 2400 bits.
 Table III 100
 Iterative Decoding Threshold:Code Rate 2/3
 MIMO Configuration 3-Sigma Optimized 10-1
 10 × 10 14.09 4.89
 40 × 40 11.52 4.39
 -2
 100 × 100 11.71 4.42 10
 BER
 10-3
 Table IV
 Iterative Decoding Threshold:Code Rate 3/4.
 -4
 MIMO Configuration 3-Sigma Optimized 10
 × 3-Sigma Quant.
 10 10 15.99 6.46 Optimized Quant.
 40 × 40 15.99 5.71
 100 × 100 15.99 5.67 6 6.2 6.4 6.6 6.8 7 7.2 7.4 7.6 7.8 8
 E /N
 b 0
 The iterative decoding thresholds for coding rates
1/2, 2/3, and 3/4 are given in Table II, Table III, and Ta- Figure 4. BER performance: 40 × 40 MIMO Configuration, Coding
 rate R = 1/2, Coded blocklength = 2400 bits.
ble IV, respectively. As expected, the iterative decoding
thresholds for the optimized quantizer are significantly
lower than the 3-sigma (conventional) quantizer in all 0
MIMO configurations. The threshold gaps vary from 2 10
dB (at coding rate 1/2) to 10 dB (at coding rate 3/4).
Therefore, one should expect huge gaps between the 10-1
BER curves of the two quantization schemes. To be
specific, the optimized 1-bit ADC will have much high-
performance merit or very low BER at the same level 10-2
of signal to noise ratio (SNR). This analytical finding
will be verified by simulation results in the below BER
 -3
subsection. 10
4.2 Bit Error Rate Performance 10-4
 In this section, the simulation results, as shown in 3-Sigma Quant.
 Optimized Quant.
Figures 3-11, are provided to verify the analytical re-
sults in Subsection 4.1. It is immediately seen that the 6 6.2 6.4 6.6 6.8 7 7.2 7.4 7.6 7.8 8
 E /N
BER curves of the optimized quantizer are far lower b 0
than those of the 3-sigma quantizer for the whole
considered range of SNR. This phenomenon is in good Figure 5. BER performance: 100 × 100 MIMO Configuration, Coding
agreement with the finding from the analytical results. rate R = 1/2, Coded blocklength = 2400 bits.
H. N. Dang et al.: On the Performance of 1-Bit ADC in Massive MIMO Communication Systems 69
 100 100
 10-1
 10-1
 10-2
 10-2
 BER
 BER
 10-3
 10-3
 10-4
 3-Sigma Quant. 3-Sigma Quant.
 Optimized Quant. Optimized Quant.
 10-4
 6 7 8 9 10 11 12 13 10 12 14 16 18 20 22 24 26 28 30
 E /N E /N
 b 0 b 0
Figure 6. BER performance: 10 × 10 MIMO Configuration, Coding Figure 9. BER performance: 10 × 10 MIMO Configuration, Coding
rate R = 2/3, Coded blocklength = 2400 bits. rate R = 3/4, Coded blocklength = 2400 bits.
 0
 100 10
 10-1
 10-1
 10-2
 10-2
 BER
 BER
 10-3
 10-3
 10-4
 3-Sigma Quant. 3-Sigma Quant.
 Optimized Quant. Optimized Quant.
 10-4
 6 7 8 9 10 11 12 13 10 12 14 16 18 20 22 24 26 28 30
 E /N E /N
 b 0 b 0
Figure 7. BER performance: 40 × 40 MIMO Configuration, Coding Figure 10. BER performance: 40 × 40 MIMO Configuration, Coding
rate R = 2/3, Coded blocklength = 2400 bits. rate R = 3/4, Coded blocklength = 2400 bits.
 0
 10 100
 10-1
 10-1
 10-2
 10-2
 BER
 BER
 10-3
 10-3
 10-4
 3-Sigma Quant. 3-Sigma Quant.
 Optimized Quant. Optimized Quant.
 10-4
 6 7 8 9 10 11 12 13 10 15 20 25
 E /N E /N
 b 0 b 0
Figure 8. BER performance: 100 × 100 MIMO Configuration, Coding Figure 11. BER performance: 100 × 100 MIMO Configuration, Coding
rate R = 2/3, Coded blocklength = 2400 bits. rate R = 3/4, Coded blocklength = 2400 bits.
70 REV Journal on Electronics and Communications: Article scheduled for publication in Vol. 10, No. 3–4, July–December, 2020
Note that the BER gaps are not the same as the iterative Hung N. Dang’s research was supported by the Do-
decoding threshold gaps since the LS-MIMO-PEXIT mestic Scholarship Programme of Vingroup Innovation
is designed using an approximation method [12, 16]. Foundation under Grant number VINIF.2019.TS.30
Therefore, the iterative decoding threshold only helps
to indicate the behavior tendency, not the absolute
metric to evaluate the performance. References
 The 3-sigma quantizer has poor performance in all
coding rates and MIMO configurations. Even the num- [1] D. C. Araújo, T. Maksymyuk, A. L. F. de Almeida,
 T. Maciel, J. C. M. Mota, and M. Jo, “Massive MIMO:
ber of transmitting and receiving antennas is in the survey and future research topics,” IET Communications,
order of 100, the BER performance of the 3-sigma vol. 10, no. 15, pp. 1938–1946, 2016.
quantizer is still floored. This observation means that [2] K. B. Letaief, W. Chen, Y. Shi, J. Zhang, and Y. A. Zhang,
the truncation limit is especially important for 1-ADCs. “The roadmap to 6G: AI empowered wireless networks,”
This fact was proved from the information-theoretical IEEE Communications Magazine, vol. 57, no. 8, pp. 84–90,
 Aug. 2019.
work in [15]. Nevertheless, for higher resolution (i.e., [3] Z. Zhang, Y. Xiao, Z. Ma, M. Xiao, Z. Ding, X. Lei, G. K.
from 2-bit ADCs to 5-bit ADCs), the 3-sigma is still con- Karagiannidis, and P. Fan, “6G wireless networks: Vi-
verged in both coded [12] and uncoded communication sion, requirements, architecture, and key technologies,”
systems [23]. IEEE Vehicular Technology Magazine, vol. 14, no. 3, pp.
 28–41, Sep. 2019.
 Look at the performance of the optimized quantizer [4] L. Fan, S. Jin, C. Wen, and H. Zhang, “Uplink achievable
alone, the slopes of the BER curves at the coding rate for massive MIMO systems with low-resolution
rate of 1/2 are steepest, and the BER performance is ADC,” IEEE Communications Letters, vol. 19, no. 12, pp.
smooth and stable in all the MIMO configurations. 2186–2189, Dec. 2015.
Nevertheless, at the coding rate of 2/3, the performance [5] W. Fukuda, T. Abiko, T. Nishimura, T. Ohgane,
 Y. Ogawa, Y. Ohwatari, and Y. Kishiyama, “Low-
is significantly degraded when the MIMO configuration complexity detection based on belief propagation in
is 10 × 10. The performance is extremely destroyed a massive MIMO system,” in Proceedings of the IEEE
at a higher coding rate (R = 3/4). In particular, the Vehicular Technology Conference (VTC), Jun. 2013, pp. 1–5.
BER curve is floored at BER = 10−2 with the 10 × 10 [6] C. Zhang, Y. Jing, Y. Huang, and X. You, “Massive
MIMO configuration. When the number of antennas MIMO with ternary ADCs,” IEEE Signal Processing Let-
 ters, vol. 27, pp. 271–275, 2020.
increases to 40 or 100, the BER curves indicate the [7] T. Liu, J. Tong, Q. Guo, J. Xi, Y. Yu, and Z. Xiao,
performance improvement. The observing results imply “Energy efficiency of massive MIMO systems with low-
that 1-ADCs should be used in the massive MIMO so resolution adcs and successive interference cancellation,”
that the negative effect of the quantization distortion IEEE Transactions on Wireless Communications, vol. 18,
is relieved by a massive number of receiving antennas. no. 8, pp. 3987–4002, Aug. 2019.
 [8] J. Dai, J. Liu, J. Wang, J. Zhao, C. Cheng, and J. Wang,
This finding was found via the information-theoretical “Achievable rates for full-duplex massive MIMO sys-
analysis for uplink MIMO multiuser scenarios [11]. tems with low-resolution ADCs/DACs,” IEEE Access,
 The experiment results in this research also suggest vol. 7, pp. 24 343–24 353, 2019.
that the protograph LDPC codes should be re-designed [9] S. Gao, P. Dong, Z. Pan, and G. Y. Li, “Deep learn-
to combat the effect of the quantization distortion for ing based channel estimation for massive MIMO with
 mixed-resolution ADCs,” IEEE Communications Letters,
the high coding rate, for example, R = 2/3, and R = vol. 23, no. 11, pp. 1989–1993, Nov. 2019.
3/4. The code design framework will be presented in [10] L. V. Nguyen, D. T. Ngo, N. H. Tran, A. L. Swindlehurst,
another report. and D. H. N. Nguyen, “Supervised and semi-supervised
 learning for MIMO blind detection with low-resolution
 ADCs,” IEEE Transactions on Wireless Communications,
 vol. 19, no. 4, pp. 2427–2442, 2020.
5 Conclusion [11] L. Xu, X. Lu, S. Jin, F. Gao, and Y. Zhu, “On the uplink
 achievable rate of massive MIMO system with low-
This paper investigates and evaluates the performance resolution ADC and RF impairments,” IEEE Communi-
of 1-bit ADCs with the 3-sigma and optimized uniform cations Letters, vol. 23, no. 3, pp. 502–505, Mar. 2019.
quantizer. The optimized quantizer brings significant [12] T. V. Nguyen, H. D. Vu, D. N. Nguyen, and H. T. Nguyen,
BER performance improvement. Besides, the research “Performance analysis of protograph LDPC codes over
 large-scale MIMO channels with low-resolution ADCs,”
suggests that one should use a large number of an- IEEE Access, vol. 7, pp. 145 145–145 160, 2019.
tennas to relieve the negative effect of the quantization [13] Y. Cho and S. Hong, “One-bit successive-cancellation
distortion of 1-bit ADC, especially for a high coding soft-output (OSS) detector for uplink MU-MIMO sys-
rate. It is worth re-designing the protograph LDPC tems with one-bit ADCs,” IEEE Access, vol. 7, pp. 27 172–
codes for this particular case of 1-bit ADCs for the 27 182, 2019.
 [14] F. Mousavi and A. Tadaion, “A simple two-stage detector
massive MIMO coded communication systems. for massive MIMO systems with one-bit ADCs,” in
 Proceedings of the 27th Iranian Conf. Electrical Engineering
 (ICEE), Apr. 2019, pp. 1674–1678.
6 Acknowledgement [15] H. Dang, T. Nguyen, and H. Nguyen, “Improve uplink
 achievable rate for massive MIMO systems with low-
 resolution adcs,” in Accepted for 20th IEEE Conference on
This research is funded by Vietnam National Founda- Communications and Electronics (ICCE), Phu Quoc, Viet-
tion for Science and Technology Development (NAFOS- nam, Jan. 2021.
TED) under grant number 102.04-2016.23 [16] H. D. Vu, T. V. Nguyen, D. N. Nguyen, and H. T. Nguyen,
H. N. Dang et al.: On the Performance of 1-Bit ADC in Massive MIMO Communication Systems 71
 “On design of protograph LDPC codes for large-scale Hung N. Dang received the B.Sc and M.Sc
 MIMO systems,” IEEE Access, vol. 8, pp. 46 017–46 029, degrees in information technology from Posts
 2020. and Telecommunications Institute of Technol-
[17] D. Tse and P. Viswanath, Fundamentals Of Wireless Com- ogy (PTIT), Hanoi, Vietnam. He is currently
 munication. Cambridge University Press, 2005. a lecturer of Faculty of Information Technol-
 ogy, Posts and Telecommunications Institute
[18] M. Srinivasan and S. Kalyani, “Analysis of massive of Technology (PTIT), Hanoi, Vietnam. His re-
 MIMO with low-resolution ADC in Nakagami-m fad- search interests lie in Massive MIMO commu-
 ing,” IEEE Communications Letters, vol. 23, no. 4, pp. 764– nications, channel coding design and analysis,
 767, Apr. 2019. wireless sensor networks.
[19] A. Gersho and R. M. Gray, Vector Quantization And Signal
 Compression. Kluwer Academic Publisher, 1992.
[20] Y. Xiong, N. Wei, and Z. Zhang, “A low-complexity
 iterative GAMP-based detection for massive MIMO with
 low-resolution ADCs,” in Proceedings of the IEEE WCNC,
 Thuy V. Nguyen received the B.Sc, M.Sc. and
 Mar. 2017, pp. 1–6. Ph.D. degrees in electrical engineering from
[21] D. Hui and D. L. Neuhoff, “Asymptotic analysis of Hanoi University of Science and Technology
 optimal fixed-rate uniform scalar quantization,” IEEE (HUST), Hanoi, Vietnam, New Mexico State
 Transactions on Information Theory, vol. 47, no. 3, pp. 957– University, Las Cruces, NM, USA, and the
 977, Mar. 2001. University of Texas at Dallas, Richardson, TX,
[22] T. Takahashi, S. Ibi, and S. Sampei, “On normalization of USA, respectively. He is currently a lecturer of
 matched filter belief in gabp for large MIMO detection,” Faculty of Information Technology, Posts and
 in Proc. IEEE Vehicular Technology Conference (VTC), Sep. Telecommunications Institute of Technology
 2016, pp. 1–6. (PTIT), Hanoi, Vietnam. Before joining PTIT,
 he was a Member of Technical Staff with Flash
[23] H. D. Vu, T. V. Nguyen, T. B. T. Do, and H. T. Nguyen, Channel Architecture, Seagate, Fremont, CA, USA. His research
 “Belief propagation detection for large-scale MIMO sys- interests lie in the areas of coding theory and its applications in next-
 tems with low-resolution ADCs,” in Proceedings of the generation communication systems.
 International Conference on Advanced Technologies for Com-
 munications (ATC), 2019, pp. 68–73.
[24] S. ten Brink, G. Kramer, and A. Ashikhmin, “Design
 of low-density parity-check codes for modulation and
 detection,” IEEE Transactions on Communications, vol. 52, Hieu T. Nguyen received the B.Sc., M.Sc. and
 no. 4, pp. 670–678, Apr. 2004. Ph.D. degrees in electrical engineering from
 Hanoi University of Science and Technology,
 University of Saskatchewan, Canada and Nor-
 wegian University of Science and Technology,
 respectively. He is a faculty member of Faculty
 of Technology, Natural Sciences, and Mar-
 itime Sciences, University of South-Eastern
 Norway (USN).