Numerical investigation of fluid – structure interaction (FSI) on sodium leakage accident at prototype fast breeder reactor monju

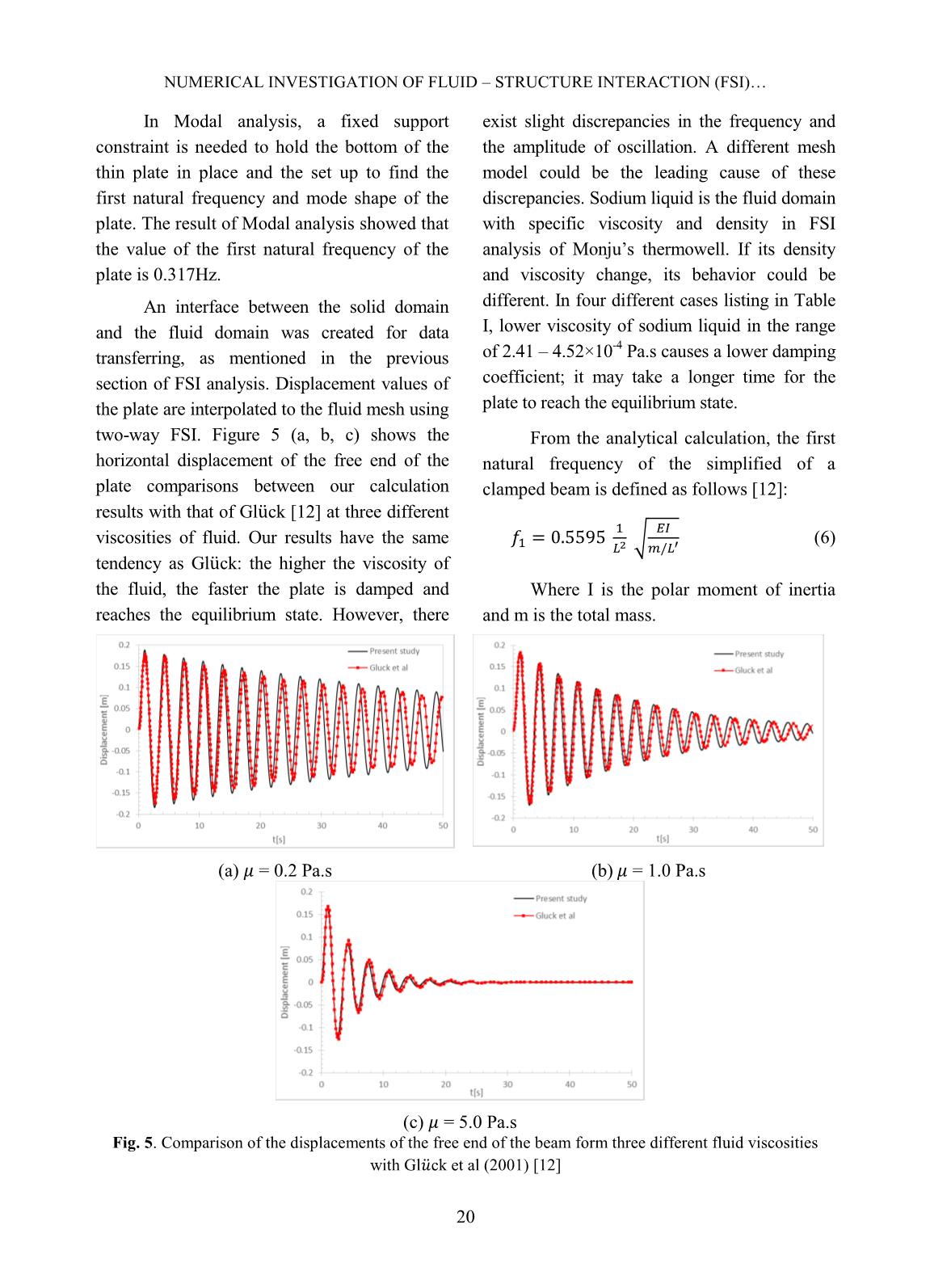
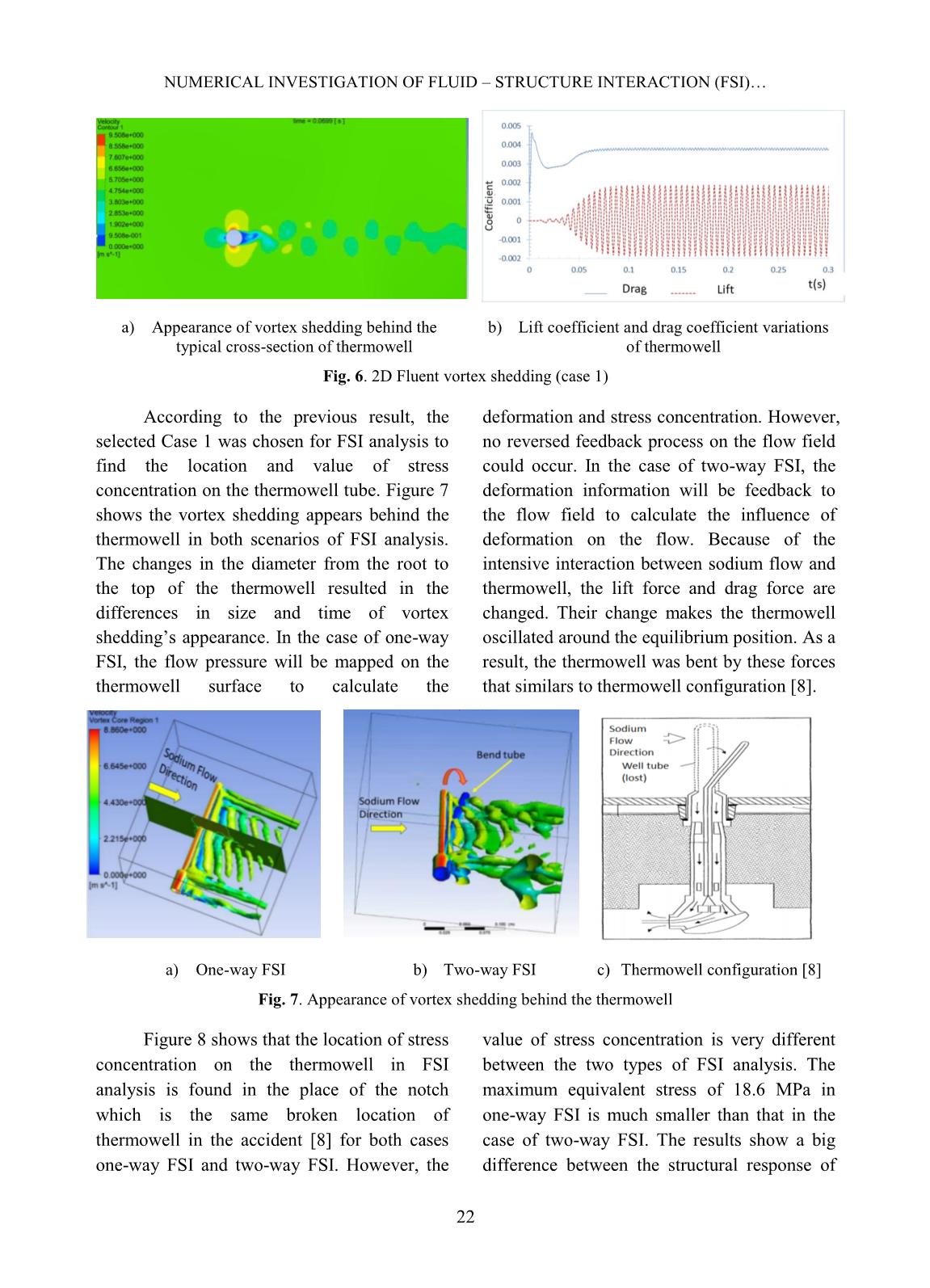
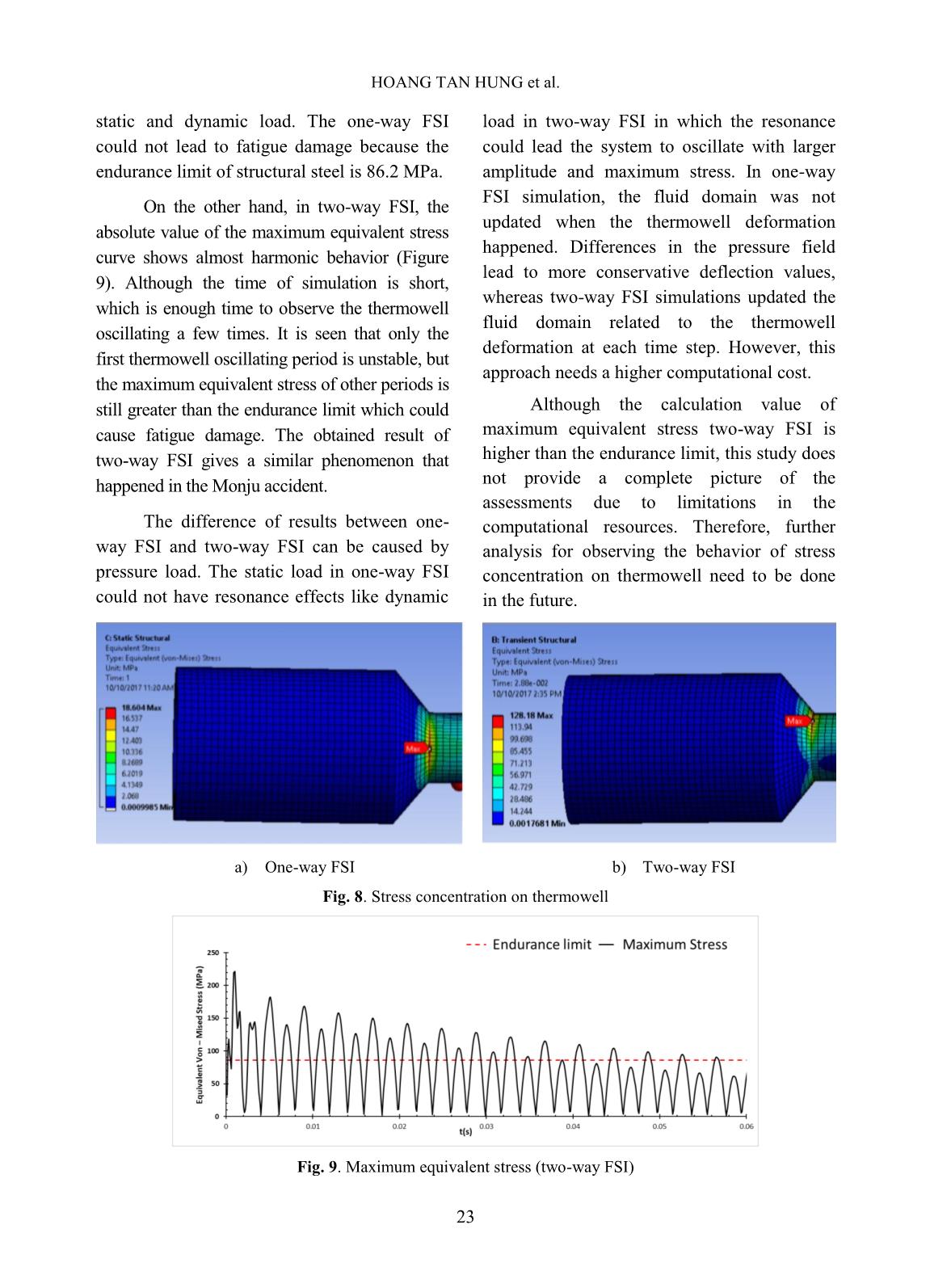
of the structure. Displacement 
values are interpolated to the fluid mesh which 
results in deformation of the fluid domain. 
In summary, the one-way FSI approach 
uses only the traction equilibrium, Eq. 5, and the 
data is transferred from Fluent solver to the 
Structure solver. In contrast, the two-way FSI 
approach uses both the traction equilibrium, Eq. 5, 
and the displacement continuity condition, Eq. 4. 
Through the two-way FSI process using both 
Eq. 4 and 5, displacement values are updated to 
the fluid mesh. 
C. Verification of the Modal and FSI 
calculation models 
To demonstrate further the validity of 
the Modal and FSI calculation models with 
oscillation problems, the oscillation of an 
exemplary vertical plate in a cavity filled 
with fluid was investigated. Figure 4 shows 
a schematic diagram of the oscillation 
problem [12]. 
A thin plate is anchored to the bottom 
of a closed cavity filled with fluid. There is no 
friction between the plate and the side of the 
cavity. During the first 0.5 seconds, a 
uniformly distributed load of 30 N/m is 
applied to distort it. Once this load is released, 
the plate oscillates back and forth to regain its 
equilibrium, and the surrounding air damps 
this oscillation. The flexible plate has 
Young’s modulus of E = 2.5 MPa, a Poisson’s 
ratio of = 0.35, and a density of 2550 kg/m3. 
The simulation with fluid density is = 
1kg/m
3
, and three different dynamic viscosities 
of the fluid = 0.2, 1.0, and 5.0 Pa.s are 
considered for the flow conditions. 
Fig. 4. Geometry of oscillating plate 
(not drawn to scale) 
NUMERICAL INVESTIGATION OF FLUID – STRUCTURE INTERACTION (FSI) 
20 
In Modal analysis, a fixed support 
constraint is needed to hold the bottom of the 
thin plate in place and the set up to find the 
first natural frequency and mode shape of the 
plate. The result of Modal analysis showed that 
the value of the first natural frequency of the 
plate is 0.317Hz. 
An interface between the solid domain 
and the fluid domain was created for data 
transferring, as mentioned in the previous 
section of FSI analysis. Displacement values of 
the plate are interpolated to the fluid mesh using 
two-way FSI. Figure 5 (a, b, c) shows the 
horizontal displacement of the free end of the 
plate comparisons between our calculation 
results with that of Gl ̈ck [12] at three different 
viscosities of fluid. Our results have the same 
tendency as Gl ̈ck: the higher the viscosity of 
the fluid, the faster the plate is damped and 
reaches the equilibrium state. However, there 
exist slight discrepancies in the frequency and 
the amplitude of oscillation. A different mesh 
model could be the leading cause of these 
discrepancies. Sodium liquid is the fluid domain 
with specific viscosity and density in FSI 
analysis of Monju’s thermowell. If its density 
and viscosity change, its behavior could be 
different. In four different cases listing in Table 
I, lower viscosity of sodium liquid in the range 
of 2.41 – 4.52×10-4 Pa.s causes a lower damping 
coefficient; it may take a longer time for the 
plate to reach the equilibrium state. 
From the analytical calculation, the first 
natural frequency of the simplified of a 
clamped beam is defined as follows [12]: 
 √
 (6) 
Where I is the polar moment of inertia 
and m is the total mass. 
(a) = 0.2 Pa.s (b) = 1.0 Pa.s 
(c) = 5.0 Pa.s 
Fig. 5. Comparison of the displacements of the free end of the beam form three different fluid viscosities 
with Gl ̈ck et al (2001) [12]
HOANG TAN HUNG et al. 
21 
However, our result only showed the 
displacement of the plate in time. Therefore, 
FFT is used to find the frequency of the plate to 
compare it with the analytical calculations. 
Applying the FFT of the displacements to the 
case of the dynamic viscosity of 0.2 Pa.s, the 
first natural frequency of the plate can be found, 
f= 0.319 Hz. The analytical value of = 0.300 
Hz is approximately equal to the simulation 
value of Modal analysis 0.317 Hz (5.6% 
difference) and FSI analysis 0.319 Hz (6.3 % 
difference). It can be seen that the characteristic 
of the oscillation of the plate is nearly the same 
with the thermowell on the Monju reactor. 
Therefore, the Modal and FSI calculation 
models can be applied for fundamental analysis 
of the oscillation of thermowell. 
III. RESULTS AND DISCUSSION 
Because the lock-in can occur when the 
frequency of vortex shedding (fs) is close to 
one of the natural frequencies (fi) of structures, 
the Modal simulation set up to find the first six 
natural frequencies of thermowell. Table II 
shows the results of Modal analysis, the value 
of frequencies are nearly equal in pair because 
of the symmetry characteristic of the geometry 
model of y and z-direction. 
Table II. Natural frequency of thermowell 
Mode 1 2 3 4 5 6 
Natural 
frequency 
fN (Hz) 
261.15 261.22 1611.70 1612.00 4327.20 4327.50 
Four cases of 2D Fluent analysis were 
performed to find the frequency of vortex 
shedding (fs) of each flow condition with a 
typical cross-section of thermowell. The 
velocity of sodium flow is 5.20 m/s and 2.08 
m/s, corresponding to the 100% and 40% flow 
operation. Figure 6 shows that the vortex 
shedding appears behind the thermowell, and 
the change of drag and lift forces coefficient is 
periodical in Case 1. The frequency of vortex 
shedding (fs) of each case is found by using 
FFT. A detailed comparison between the 
average natural frequency of structure (fN) and 
vortex frequency fo fluid (fS) for Mode 1 and 
Mode 2 is shown in Table III. From Eq. 2, it can 
be seen that the safe cases could be reached if 
the frequency ratio, f, is smaller than 0.40, and it 
could be dangerous in reverse situations. Except 
for Mode 1 and 2, it can be seen that f is much 
smaller than 0.40 in other modes with higher 
frequencies. The most dangerous case could 
occur in Mode 1 and 2. Therefore, higher 
natural frequency comparisons are not necessary. 
The results show that the most dangerous case 
of flow condition can lead to fatigue damage is 
Case 1 with ratio f = fS/ fN = 0.65. The obtained 
result in Case 1 was in good agreement with that 
in [1]. 
Table III. Comparison of natural frequency of thermowell and vortex shedding frequency 
 Vortex shedding 
frequency fS (Hz) 
Average natural frequency fN 
(Mode 1 and mode 2) (Hz) 
Ratio f = fS/ fN 
Case 1 170.94 261.185 0.65 
Case 2 64.10 261.185 0.25 
Case 3 64.10 261.185 0.25 
Case 4 64.10 261.185 0.25 
NUMERICAL INVESTIGATION OF FLUID – STRUCTURE INTERACTION (FSI) 
22 
a) Appearance of vortex shedding behind the 
typical cross-section of thermowell 
b) Lift coefficient and drag coefficient variations 
of thermowell 
Fig. 6. 2D Fluent vortex shedding (case 1) 
According to the previous result, the 
selected Case 1 was chosen for FSI analysis to 
find the location and value of stress 
concentration on the thermowell tube. Figure 7 
shows the vortex shedding appears behind the 
thermowell in both scenarios of FSI analysis. 
The changes in the diameter from the root to 
the top of the thermowell resulted in the 
differences in size and time of vortex 
shedding’s appearance. In the case of one-way 
FSI, the flow pressure will be mapped on the 
thermowell surface to calculate the 
deformation and stress concentration. However, 
no reversed feedback process on the flow field 
could occur. In the case of two-way FSI, the 
deformation information will be feedback to 
the flow field to calculate the influence of 
deformation on the flow. Because of the 
intensive interaction between sodium flow and 
thermowell, the lift force and drag force are 
changed. Their change makes the thermowell 
oscillated around the equilibrium position. As a 
result, the thermowell was bent by these forces 
that similars to thermowell configuration [8]. 
a) One-way FSI b) Two-way FSI c) Thermowell configuration [8] 
Fig. 7. Appearance of vortex shedding behind the thermowell 
Figure 8 shows that the location of stress 
concentration on the thermowell in FSI 
analysis is found in the place of the notch 
which is the same broken location of 
thermowell in the accident [8] for both cases 
one-way FSI and two-way FSI. However, the 
value of stress concentration is very different 
between the two types of FSI analysis. The 
maximum equivalent stress of 18.6 MPa in 
one-way FSI is much smaller than that in the 
case of two-way FSI. The results show a big 
difference between the structural response of 
HOANG TAN HUNG et al. 
23 
static and dynamic load. The one-way FSI 
could not lead to fatigue damage because the 
endurance limit of structural steel is 86.2 MPa. 
On the other hand, in two-way FSI, the 
absolute value of the maximum equivalent stress 
curve shows almost harmonic behavior (Figure 
9). Although the time of simulation is short, 
which is enough time to observe the thermowell 
oscillating a few times. It is seen that only the 
first thermowell oscillating period is unstable, but 
the maximum equivalent stress of other periods is 
still greater than the endurance limit which could 
cause fatigue damage. The obtained result of 
two-way FSI gives a similar phenomenon that 
happened in the Monju accident. 
The difference of results between one-
way FSI and two-way FSI can be caused by 
pressure load. The static load in one-way FSI 
could not have resonance effects like dynamic 
load in two-way FSI in which the resonance 
could lead the system to oscillate with larger 
amplitude and maximum stress. In one-way 
FSI simulation, the fluid domain was not 
updated when the thermowell deformation 
happened. Differences in the pressure field 
lead to more conservative deflection values, 
whereas two-way FSI simulations updated the 
fluid domain related to the thermowell 
deformation at each time step. However, this 
approach needs a higher computational cost. 
Although the calculation value of 
maximum equivalent stress two-way FSI is 
higher than the endurance limit, this study does 
not provide a complete picture of the 
assessments due to limitations in the 
computational resources. Therefore, further 
analysis for observing the behavior of stress 
concentration on thermowell need to be done 
in the future. 
a) One-way FSI b) Two-way FSI 
Fig. 8. Stress concentration on thermowell 
Fig. 9. Maximum equivalent stress (two-way FSI) 
NUMERICAL INVESTIGATION OF FLUID – STRUCTURE INTERACTION (FSI) 
24 
IV. CONCLUSIONS 
In this study, two approaches of one-way 
FSI and two-way FSI using for analysis were 
performed to investigate the VIV 
phenomenon and the stress concentration 
location and the stress amplitude acting on 
Monju’s thermowell. The flow condition 
with maximum stress was chosen for FSI 
analysis to find the most severe case leading 
to thermowell fatigue damage. The obtained 
result shows that fatigue damage initiated at 
an early stage of the 100% flow operation. 
- In both approaches, the vortex 
shedding appears behind the thermowell. The 
changes in the diameter from the root to the top 
of the thermowell resulted in the differences in 
size and time of vortex shedding’s appearance. 
- The one-way FSI approach predicts 
well the stress concentration location. However, 
the value of the maximum equivalent stress at 
that location is not predicted with enough 
accuracy. In opposite, for the two-way FSI, it 
could predict both the stress concentration 
location and the value of the maximum 
equivalent stress at that location. Therefore, a 
two-way FSI approach for the evaluation of the 
stress on the thermowell of the Monju reactor 
is suitable. 
- Fatigue damage could occur in the 
condition of the maximum value of stress getting 
higher than the endurance limit. This condition is 
reached in our analysis using two-way FSI. 
However, it is needed a longer time of simulation 
to observe the change in the stress amplitude for 
the overall fatigue damage process. 
ACKNOWLEDGMENTS 
The authors of this paper wish to express 
their appreciation for the financial support from 
VIETNAM ATOMIC ENERGY INSTITUTE 
(VINATOM) through the R&D Project: "Fluid – 
Structure Interaction (FSI) of sodium leakage 
incident at prototype fast breeder reactor Monju 
by ANSYS". 
REFERENCES 
[1]. H. Mikami, A. Shono and H. Hiroi, “Sodium 
Leak at Monju (I) - Cause and Consequences”, 
Tech. Committee Meeting on Evaluation of 
Radioactive Materials Release and Sodium 
Fires in Fast Reactors, Oaria, Ibaraki, Japan, 
International Atomic Energy Agency, Vienna, 
Austria, 1996. 
 [2]. Masaya Kondo, Yoshinari Anoda, “Water 
Flow Simulation Test on Flow – Induced 
Oscillation of Thermowell in Prototype Fast 
Breeder Reactor MONJU”, JSME International 
Journal, Serires B, Vol.4, No.4, 2001. 
[3]. Hideki Aoi, Yue Zhao, Tamotsu Hayase, 
“Improvement of the Damaged Thermowell of 
the Monju Fast-Breeder Reactor Based on 
Vibration Analysis”, The Society for Modeling 
and Simulation International, SIMULATION, 
Vol. 78, Issue 8 , p. 504-511, 2002. 
[4]. Sebastian Kornet, Daniel Sławiński, Paweł 
Ziółkowski, Janusz Badur, “Analysis of 
unsteady flow forces on the thermowell of 
steam temperature sensor”, Transactions of the 
Institute of Fluid-Flow Machinery, No. 129, p. 
25–49, 2015. 
[5]. AISI Type 304 Stainless Steel, [online] 
Available at: 
x?matguid=bd20a4281ae3430d97cfbebf6904e
c50&ckck=1. 
[6]. Masaki Morishita, Yusaku Wada, “Fatigue 
analysis of thermowell due to flow – induced 
vibration”, Flow – Induced Vibration and 
Transient Thermal – Hydraulics, ASME 
International, p. 120, 1998. 
HOANG TAN HUNG et al. 
25 
[7]. J.K.Fink, L.Leibowitz, “Thermodynamic and 
Transport Properties of Sodium Liquid and 
Vapor”, Argonne National Laboratory, pp. 86-
95 and p. 207, 1995. 
[8]. A.Miyakawa, H.Maeda, Y.Kami, K.Ito, 
“Sodium Leakage Experience at the Prototype 
FBR Monju”, Unusual Occurrences during 
LMFR Operation, IAEA-TECDOC-1180, 
Vienna (Austria), p. 43 -56, 1998. 
[9] Anton Gustafsson, “Analysis of Vortex-
Induced Vibrations of Rises”, Master’s thesis 
in Applied Mechanics, Chalmers University Of 
Technology, Sweden 2012. 
[10]. Brauschke D., Wiklund D., Kitzman A., Zulic 
D., “Thermowell calculations”, Emerson 
Process Management, White Paper 00840–
0200–2654, Rev AC, p. 11, March 2014. 
[11]. ANSYS Tutorials & Training Materials, “Fluid 
Structure Interaction FSI with 
ANSYS Fluent 17.0” and “ANSYS 
Mechanical Linear and Nonlinear Dynamic”, 
ANSYS Inc, 2016. 
[12].Gl ̈ck, M., Breuer, M., Durst, F., Halfmann, A., 
Rank, E., “Computation of fluid–structure 
interaction on lightweight structures”, Journal 
of Wind Engineering and Industrial 
Aerodynamics 89, p. 1351–1368, 2001.