Nghiên cứu hiệu ứng tương quan phi điều hòa bằng mô hình debye trong phổ cấu trúc tinh tế hấp thụ tia X–áp dụng đối với hợp kim hai thành phần

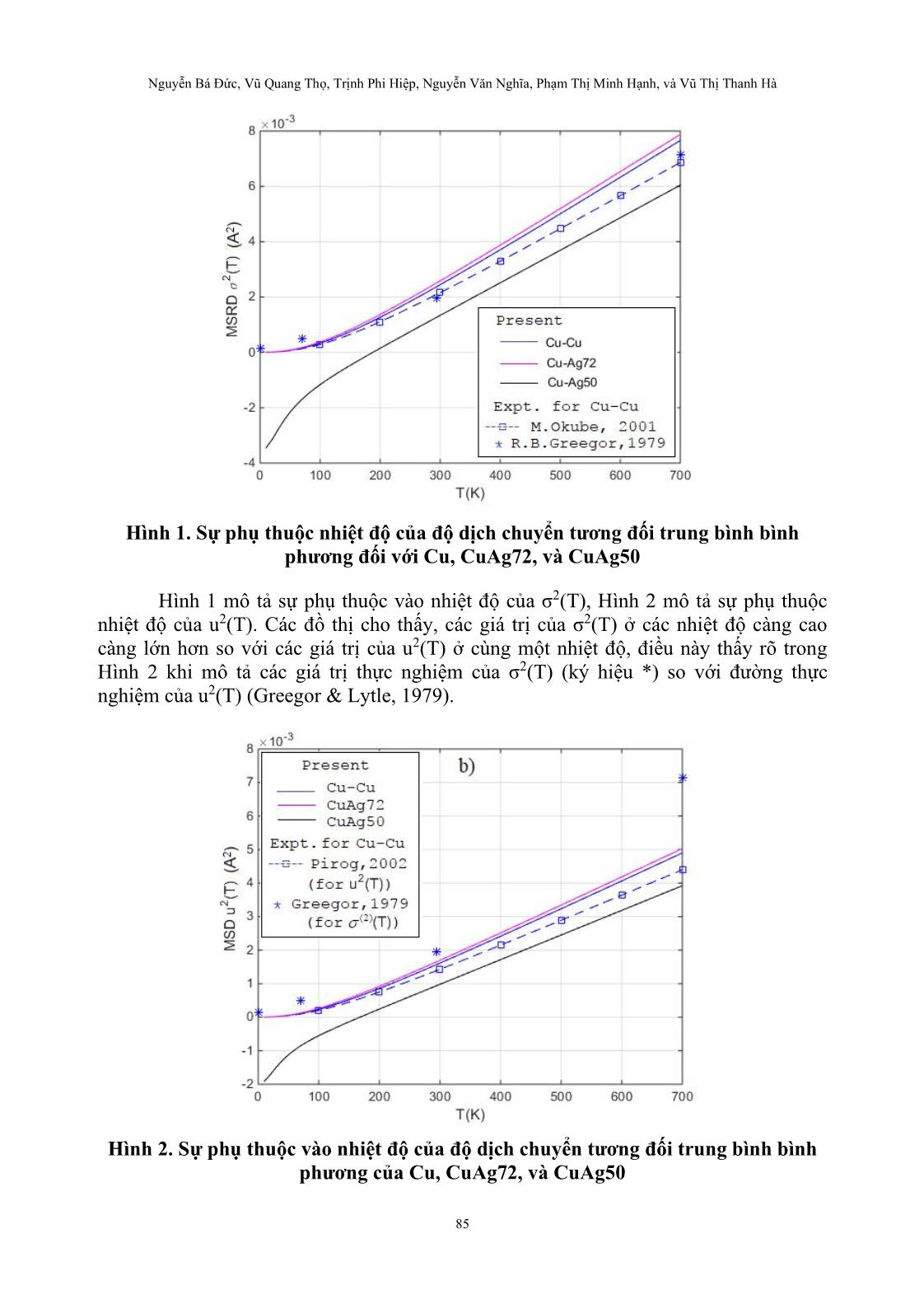
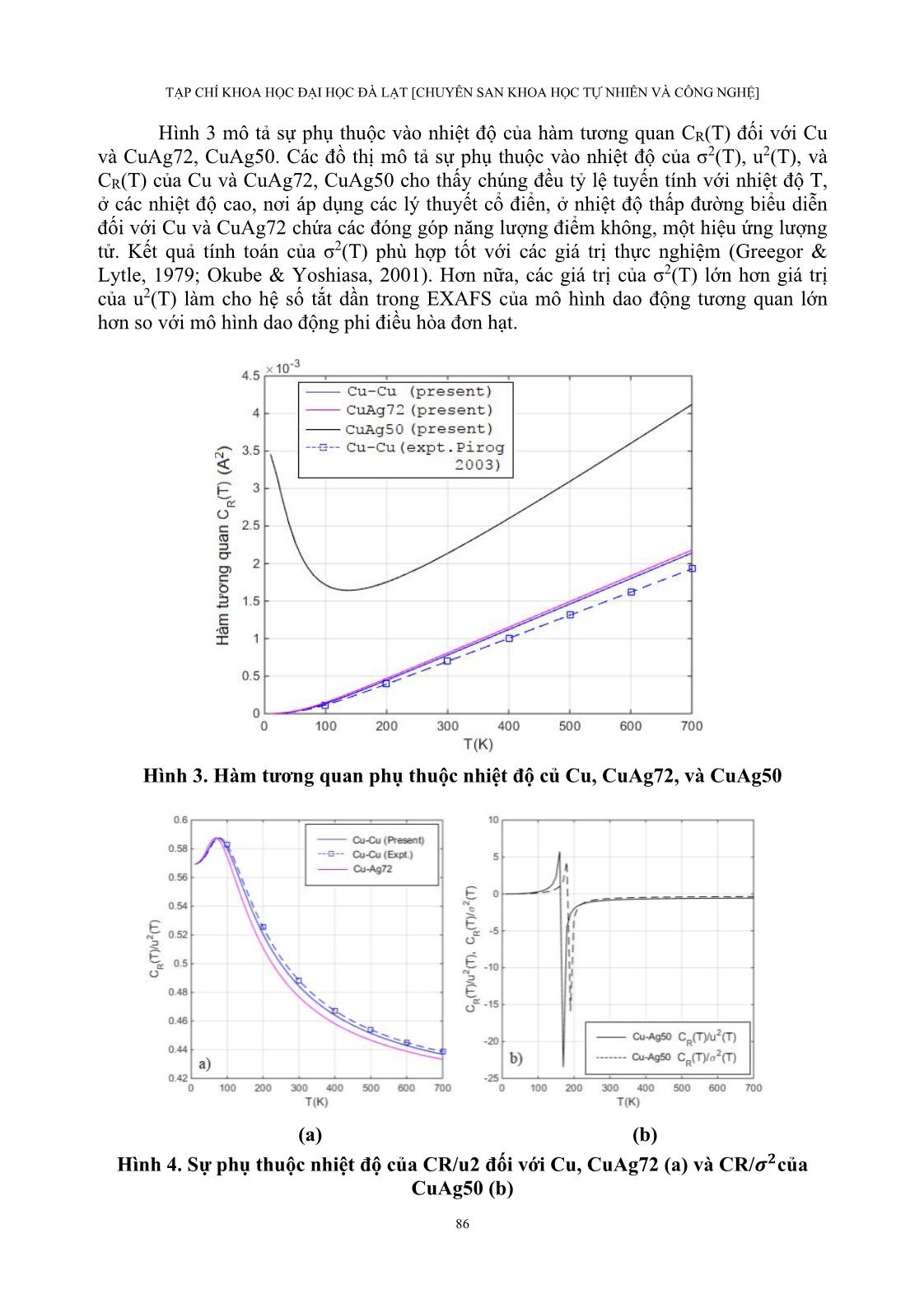
 D = + + ,
trong đó c1, c2 là tỷ lệ pha tạp của hợp kim (Nguyen & Vu, 2019). Theo mô hình Debye 
tương quan phi điều hòa, chúng ta có: 
3
1212A3
2
1212A D
4
3
k,D5k −== , (16) 
và theo mô hình Debye phi điều hòa: 
3
1212D3
2
1212D Dk,D8k −== . (17) 
Lấy đạo hàm các đại lượng nhiệt động được biểu diễn bởi Hệ thức (6), (7), (8), 
sau đó mô tả hệ trong mô hình Debye với tất cả các tần số khác nhau, mỗi tần số tương 
ứng với một sóng có tần số ω (q) và số sóng q biến thiên trong vùng Brillouin thứ nhất. 
Trên cơ sở ACDM, biểu thức của σ2(T) có dạng: 
,dq
)q(z1
)q(z1
)q(
k2
c
)T(
c/
0
A
A
A
A
2
−
+
=



 (18) 
Nguyễn Bá Đức, Vũ Quang Thọ, Trịnh Phi Hiệp, Nguyễn Văn Nghĩa, Phạm Thị Minh Hạnh, và Vũ Thị Thanh Hà 
83 
( )
2 1
( ) , ( ) 2 sin , .
2
A q A
A A
B
k qc
z q e q
M k T
   
= = = 
 (19) 
Thay thế hệ thức (16) vào (18), (19) ta có: 
 ,dq
)q(z1
)q(z1
)q(
D10
c
)T(
c/
0
A
A
A
2
1212
2
−
+
=



 (20) 
2
12 12
10
( ) 2 sin , .
2
A
D qc
q q
M c

= 
 (21) 
Tương tự, với ADM, biểu thức giải tích của u2(T) cho mô hình dao động phi 
điều hòa đơn hạt đã được xác định là: 
,dq
)q(z1
)q(z1
)q(
k2
c
)T(u
c/
0
D
D
D
D
2
−
+
=


 (22) 
( )
2
( ) , ( ) 2 sin ,
2
D q D
D D
k qc
z q e q
M
  
= = 
 (23) 
Thay thế Hệ thức (17) vào Hệ thức (22) và (23) ta có: 
,dq
)q(z1
)q(z1
)q(
D16
c
)T(u
c/
0
D
D
D
2
1212
2
−
+
=


 (24) 
2
12 12
8
( ) 2 sin , .
2
D
D qc
q q
M c

= 
 (25) 
Chú ý rằng, đại lượng z trong các phương trình (20) và (24) là biến nhiệt độ và 
có biểu thức dạng /( )( ) ,D Tqz q e e = = với 
D
 là nhiệt độ Debye. Biến đổi các tích phân 
trong (20), (24), tách phần hằng số không phụ thuộc nhiệt độ T, chúng ta sẽ có các biểu 
thức mô tả đóng góp điểm không vào σ2(T) và u2(T). 
Trong các phương trình trên, c là hằng số mạng, q là số sóng phonon và M là 
khối lượng của các nguyên tử, kB là hằng số Boltzmann,  là hằng số Planck. Từ các 
phương trình (20), (21), (24), (25) và (8), chúng ta có hàm tương quan CR(T): 
 ,
c
q,dq
)q(z1
)q(z1
)q(
k
1
dq
)q(z1
)q(z1
)q(
k
1
2
c
)T(C
c/
0
A
A
A
A
c/
0
D
D
D
D
R

 


−
+
−
−
+
= 

(26) 
Thay các tham số thế Morse đối với các tinh thể fcc vào phương trình (24), ta có: 
TẠP CHÍ KHOA HỌC ĐẠI HỌC ĐÀ LẠT [CHUYÊN SAN KHOA HỌC TỰ NHIÊN VÀ CÔNG NGHỆ] 
84 
 ,
c
q,dq
)q(z1
)q(z1
)q(
5
1
dq
)q(z1
)q(z1
)q(
4
1
D2
c
)T(C
c/
0
A
A
c/
0
D
D
D
2
1212
R

 


−
+
−
−
+
= 

(27) 
Phương trình (27) mô tả các hiệu ứng tương quan của dao động nhiệt. 
3. KẾT QUẢ VÀ THẢO LUẬN 
Áp dụng các biểu thức (20-27) để tính số đối với tinh thể Cu và các hợp kim 
CuAg72, CuAg50. Kết quả tính toán tham số thế Morse theo lý thuyết và các tham số 
thế Morse lấy từ thực nghiệm (Okube & Yoshiasa, 2001) được trình bày trong Bảng 1, 
các hằng số lực đàn hồi được tính toán và thống kê trong Bảng 2, kết quả cho thấy có sự 
phù hợp tốt giữa tính toán lý thuyết với các giá trị thu được từ thực nghiệm và các 
nghiên cứu khác (Greegor & Lytle, 1979; Okube & Yoshiasa, 2001; Pirog et al., 2002; 
Tranquada & Ingalls, 1983). Thay thế các tham số trong các Bảng 1 và 2 vào các hệ 
thức (20), (24), (27), chúng ta sẽ nhận được độ dịch chuyển tương đối trung bình bình 
phương σ2(T), độ dịch chuyển trung bình bình phương u2(T) và hàm dịch chuyển tương 
quan CR(T) của tinh thể Cu và các hợp kim CuAg72, CuAg50. 
Bảng 1. Các tham số thế Morse theo lý thuyết (LT) và giá trị thực nghiệm (TN) 
Đại lượng/ Tinh thể D12(eV) 
(LT) 
D12(eV) 
 (TN) 
)Å( -112 
(LT) 
)Å( -112 
(TN) 
Cu-Cu 0.3429 0.3528 1.3588 1.4072 
CuAg72 0.3381 - 1.3634 - 
CuAg50 0.3376 - 1.3638 - 
Bảng 2. Hằng số lực đàn hồi theo lý thuyết (LT) và giá trị thực nghiệm (TN) 
Đại lượng/ 
tinh thể 
kA(eVA-2) 
(LT) 
kA(eVA-2) 
(TN) 
kD(eVA-2) 
(LT) 
kD(eVA-2) 
(TN) 
k3A(eVA-3) 
 (LT) 
k3A(eVA-3) 
 (TN) 
k3D(eVA-3) 
 (LT) 
k3D(eVA-3) 
 (TN) 
Cu-Cu 3.1655 3.4931 5.5889 5.7520 0.6646 0.8070 3.0889 0.9831 
CuAg72 3.1423 - 5.0278 - 0.6814 - 2.6874 - 
CuAg50 3.1396 - 5.0234 - 0.6423 - 0.8569 - 
Số liệu trong các Bảng 1 và 2 cho thấy sự khác biệt đáng kể giữa mô hình dao 
động tương quan và mô hình dao động phi điều hòa đơn hạt. Hằng số lực của dao động 
phi điều hòa đơn hạt (ADM) kD lớn hơn nhiều so với kA của dao động tương quan 
(ACDM). Lý do cho sự khác nhau này là từ cách xác định số lượng và khối lượng các 
nguyên tử dao động của hai mô hình khác nhau. Đối với mô hình dao động tương quan, 
số lượng và khối lượng các nguyên tử chỉ bằng một nửa so với mô hình dao động phi 
điều hòa đơn hạt. Thực tế, nếu coi khối lượng tập trung ở tâm của liên kết đơn cho mô 
hình dao động tương quan thì một tinh thể sẽ hoạt động như với các nguyên tử bán 
phần, tức là khối lượng giảm chỉ bằng một nửa và số lượng nguyên tử cũng chỉ bằng 
một nửa số nguyên tử cho mô hình dao động phi điều hòa đơn hạt vì mỗi nguyên tử bán 
phần được tạo ra từ một cặp nguyên tử. 
Nguyễn Bá Đức, Vũ Quang Thọ, Trịnh Phi Hiệp, Nguyễn Văn Nghĩa, Phạm Thị Minh Hạnh, và Vũ Thị Thanh Hà 
85 
Hình 1. Sự phụ thuộc nhiệt độ của độ dịch chuyển tương đối trung bình bình 
phương đối với Cu, CuAg72, và CuAg50 
Hình 1 mô tả sự phụ thuộc vào nhiệt độ của σ2(T), Hình 2 mô tả sự phụ thuộc 
nhiệt độ của u2(T). Các đồ thị cho thấy, các giá trị của σ2(T) ở các nhiệt độ càng cao 
càng lớn hơn so với các giá trị của u2(T) ở cùng một nhiệt độ, điều này thấy rõ trong 
Hình 2 khi mô tả các giá trị thực nghiệm của σ2(T) (ký hiệu *) so với đường thực 
nghiệm của u2(T) (Greegor & Lytle, 1979). 
Hình 2. Sự phụ thuộc vào nhiệt độ của độ dịch chuyển tương đối trung bình bình 
phương của Cu, CuAg72, và CuAg50 
TẠP CHÍ KHOA HỌC ĐẠI HỌC ĐÀ LẠT [CHUYÊN SAN KHOA HỌC TỰ NHIÊN VÀ CÔNG NGHỆ] 
86 
Hình 3 mô tả sự phụ thuộc vào nhiệt độ của hàm tương quan CR(T) đối với Cu 
và CuAg72, CuAg50. Các đồ thị mô tả sự phụ thuộc vào nhiệt độ của σ2(T), u2(T), và 
CR(T) của Cu và CuAg72, CuAg50 cho thấy chúng đều tỷ lệ tuyến tính với nhiệt độ T, 
ở các nhiệt độ cao, nơi áp dụng các lý thuyết cổ điển, ở nhiệt độ thấp đường biểu diễn 
đối với Cu và CuAg72 chứa các đóng góp năng lượng điểm không, một hiệu ứng lượng 
tử. Kết quả tính toán của σ2(T) phù hợp tốt với các giá trị thực nghiệm (Greegor & 
Lytle, 1979; Okube & Yoshiasa, 2001). Hơn nữa, các giá trị của σ2(T) lớn hơn giá trị 
của u2(T) làm cho hệ số tắt dần trong EXAFS của mô hình dao động tương quan lớn 
hơn so với mô hình dao động phi điều hòa đơn hạt. 
Hình 3. Hàm tương quan phụ thuộc nhiệt độ củ Cu, CuAg72, và CuAg50 
(a) (b) 
Hình 4. Sự phụ thuộc nhiệt độ của CR/u2 đối với Cu, CuAg72 (a) và CR/𝝈𝟐của 
CuAg50 (b) 
Nguyễn Bá Đức, Vũ Quang Thọ, Trịnh Phi Hiệp, Nguyễn Văn Nghĩa, Phạm Thị Minh Hạnh, và Vũ Thị Thanh Hà 
87 
Hình 4 mô tả tỷ lệ tương quan giữa CR với u2 đối với Cu và CuAg72 (Hình 4), 
tương quan giữa CR với u2 và σ2 đối với CuAg50 (Hình 4). Đối với tinh thể Cu và hợp 
kim CuAg72, sự biến thiên của đường biểu diễn có dạng trùng khớp với thực nghiệm 
(Pirog et al., 2002). 
Một điều thú vị trong cả bốn đồ thị, đó là đồ thị biểu diễn của các hợp kim liên 
kim loại CuAg72 và CuAg50. Với hợp kim CuAg72, dạng đồ thị tương đồng với đồ thị 
của tinh thể Cu nguyên chất, có nghĩa cấu trúc của hợp kim CuAg72 không bị phá vỡ và 
kiểu cấu trúc vẫn là lập phương tâm diện fcc. Tuy nhiên đối với hợp kim CuAg50 thì đồ 
thị có dạng bất thường, trong các Hình 1, 2, và 3, đồ thị của CuAg50 không có đóng góp 
năng lượng điểm không và không theo quy luật như của Cu và CuAg72 ở các nhiệt độ 
thấp, từ khoảng nhiệt độ 200K trở lên, đồ thị CuAg50 trở lại dạng tuyến tính như đối 
với các tinh thể Cu và CuAg72. Đặc biệt trong Hình 4b, đồ thị của CR/u2 và CR/σ2 đối 
với CuAg50 có biến điệu bất thường tại khoảng nhiệt độ từ 140K đến 200K, nhưng từ 
khoảng 200K trở lên tỷ số tương quan bắt đầu có giá trị không đổi, trở lại đúng theo lý 
thuyết cổ điển. Sự bất thường này của các đường biểu diễn, có thể suy đoán, trong cấu 
trúc tinh thể của hợp kim Cu-Ag với tỷ lệ 50:50, các nguyên tử đã không còn liên kết 
chặt chẽ và theo kiểu cấu trúc trật tự theo mạng tinh thể fcc ở các nhiệt độ thấp (nghĩa là 
không tồn tại dạng vật liệu đồng-bạc có liên kết theo tỷ lệ 50:50 ở dải nhiệt độ 140K-
200K), khi nhiệt độ tăng cao, dao động tương quan giữa các nguyên tử thay đổi, đến khi 
nhiệt độ đạt một giá trị nhất định nào đó, trật tự mạng tinh thể fcc lại dần hồi phục. Điều 
này hoàn toàn phù hợp với một số nghiên cứu đã thực hiện bằng các lý thuyết theo mô 
hình khác và thực nghiệm đối với hợp kim Cu-Ag tỷ lệ 50:50 (Kraut & Stern, 2000; 
Nguyen & Vu, 2019). 
4. KẾT LUẬN 
Trong nghiên cứu này, các hiệu ứng tương quan mô tả qua hàm tương quan dịch 
chuyển CR(T) dựa trên DWF được thực hiện bởi độ dịch chuyển tương đối trung bình 
bình phương σ2(T) và độ dịch chuyển trung bình bình phương u2(T) trong EXAFS. Lý 
thuyết đã được xây dựng và áp dụng tính toán cho các kim loại nguyên chất có cấu trúc 
fcc và hợp kim của chúng với các tỷ lệ pha tạp khác nhau. Để xây dựng được biểu thức 
của CR(T), các biểu thức giải tích của σ2(T) và u2(T) đã được rút ra trên cơ sở các mô 
hình Debye. Lợi thế của các mô hình này là dựa trên việc sử dụng thế năng hiệu dụng 
phi điều hòa có tính đến sự đóng góp của tất cả các nguyên tử lân cận. Sự sai khác của 
hằng số lực đàn hồi hiệu dụng, giữa số lượng và khối lượng của các nguyên tử dao động 
trong các mô hình là nguyên nhân tạo nên sự khác nhau về tính chất nhiệt động. Các đại 
lượng σ2(T), u2(T) và CR(T) thu được là phụ thuộc vào nhiệt độ. Giá trị của chúng đều 
tỷ lệ tuyến tính với nhiệt độ T ở các nhiệt độ cao, tại đó ta có thể áp dụng gần đúng cổ 
điển, ở nhiệt độ thấp chúng chứa các đóng góp năng lượng điểm không, đây là một hiệu 
ứng lượng tử. 
Mạng tinh thể của hợp kim CuAg50 có sự mất trật tự bất thường tại dải nhiệt độ 
thấp (dưới 200K), các nguyên tử Cu và Ag không còn liên kết mạng tinh thể theo cấu 
trúc fcc nữa. Kết quả nghiên cứu lý thuyết bằng mô hình Debye này cũng phù hợp với 
phát hiện trong nghiên cứu thực nghiệm của Kraut và Stern (2000) và một số nghiên 
TẠP CHÍ KHOA HỌC ĐẠI HỌC ĐÀ LẠT [CHUYÊN SAN KHOA HỌC TỰ NHIÊN VÀ CÔNG NGHỆ] 
88 
cứu lý thuyết theo mô hình Einstein tương quan phi điều hòa gần đây (Nguyen, 2020; 
Nguyen & Vu, 2019), sự bất thường này có thể sẽ mang lại nhiều thú vị mới khi nghiên 
cứu sâu về hợp kim này trong tương lai đối với các nhà nghiên cứu chuyên sâu về khoa 
học vật liệu. 
Sự phù hợp tốt giữa các kết quả tính toán của nghiên cứu này với các giá trị thu 
từ thực nghiệm, cũng như phù hợp với các giá trị được tính toán bằng các mô hình khác 
đã chứng minh hiệu quả của lý thuyết hiện tại trong việc phân tích dữ liệu phổ EXAFS, 
đặc biệt là nghiên cứu các hiệu ứng tương quan. 
LỜI CẢM ƠN 
Nghiên cứu này được tài trợ bởi Quỹ Phát triển khoa học và Công nghệ Quốc 
gia (NAFOSTED) trong đề tài mã số 103.01-2019.55. 
TÀI LIỆU THAM KHẢO 
Beni, G., & Platzman, P. M. (1976). Temperature and polarization dependence of 
extended x-ray absorption fine-structure spectra. Physical Review B, 14(4), 
1514-1518. https://doi.org/10.1103/PhysRevB.14.1514. 
Frenkel, A. I., & Rehr, J. J. (1993). Thermal expansion and x-ray-absorption fine-
structure cumulants. Physical Review B, 48(1), 585-588. https://doi.org/10.1103/ 
PhysRevB.48.585. 
Greegor, R. B., & Lytle, F. W. (1979). Extended x-ray absorption fine structure 
determination of thermal disorder in Cu: Comparison of theory and experiment. 
Physical Review B, 20(12), 4902-4907. https://doi.org/10.1103/PhysRevB.20.4902. 
Hung, N. V., & Rehr, J. J. (1997). Anharmonic correlated Einstein-model Debye-Waller 
factors. Physical Review B, 56(1), 43-46. https://doi.org/10.1103/PhysRevB.56.43. 
Koningsberger, D. C., & Prins, K. (1988). Chapter 9. In E. D. Crozier, J. J. Rehr, & R. 
Ingalls (Eds), X-ray Absorption: Principles, applications, techniques of EXAFS, 
SEXAFS and XANES (pp. 373). New York, USA: Wiley Publishing. 
Kraut, J. C., & Stern, W. B. (2000). The density of gold-silver-copper alloys and its 
calculation from the chemical composition. Gold Bulletin, 33(2), 52-55. 
https://doi.org/10.1007/BF03216580. 
Nguyen, B. D. (2020). Influence of temperature and pressure on cumulants and 
thermodynamic parameters of intermetallic alloy based on anharmonic 
correlated Einstein model in EXAFS. Physica Scripta, 5(7). 
https://doi.org/10.1088/1402-4896/ab90bf. 
Nguyen, B. D., & Vu, Q. T. (2019). Dependence of cumulants and thermodynamic 
parameters on temperature and doping ratio in extended X-ray absorption fine 
structure spectra of cubic crystals. Physica B: Condensed Matter, 55(2), 1-5. 
https://doi.org/10.1016/j.physb.2018.09.038. 
Nguyễn Bá Đức, Vũ Quang Thọ, Trịnh Phi Hiệp, Nguyễn Văn Nghĩa, Phạm Thị Minh Hạnh, và Vũ Thị Thanh Hà 
89 
Nguyen, V. H., Nguyen, B. T., Nguyen, B. D., Duong, D. S., & Tong, S. T. (2014). 
Debye-Waller factor and correlation effects in XAFS of cubic crystals. Journal 
of Physical Science and Application, 4(1), 43-49. https://doi.org/10.13140/2.1. 
1296.1927. 
Nguyen, V. H., & Dinh Q. V. (2019). Correlation effects studied based on Debye 
Waller factors: Application to fcc crystals. Modern Physics Letters B, 33(20), 1-
10. https://doi.org/10.1142/S0217984919502373. 
Nguyen, V. H., Nguyen, B. T., & Kirchner, B. (2010). Anharmonic correlated Debye 
model Debye–Waller factors. Physica B, 405(11), 2519-2525. https://doi.org/ 
10.1016/j.physb.2010.03.013. 
Okube, M., & Yoshiasa, A. (2001). Anharmonic effective pair potentials of group VIII 
and Ib fcc metals. Journal of Synchrotron Radiation, 8(2), 937-939. 
https://doi.org/10.1107/s0909049500021051. 
Pirog, I. V., Nedoseikina, T. I., Zarubin, I. A., & Shuvaev, A. T. (2002). Anharmonic 
pair potential study in face-centred-cubic structure metals. Journal of Physics: 
Condensed Matter, 14(18), 1825-1832. https://doi.org/10.1088/09538984/14/8/311. 
Stern, E. A., Livins, P., & Zhang, Z. (1991). Thermal vibration and melting from a local 
perspective. Physical Review B, 43(11), 8850-8860. https://doi.org/10.1103/ 
PhysRevB.43.8850. 
Schowalter, M., Rosenauer, A., Titantah, J. T., & Lamoen, D. (2009). Computation and 
parametrization of the temperature dependence of Debye–Waller factors for 
group IV, III–V and II–VI semiconductors. Acta Cryst, A65, 5-17. 
https://doi.org/10.1107/ S0108767308031437. 
Tranquada, J. M., & Ingalls, R. (1983). Extended X-ray absorption fine-structure study 
of anharmonicity in CuBr. Physical Review B, 28(6), 3520-3528. 
https://doi.org/10.1103/PhysRevB.28.3520. 
Yokoyama, T., Sasukawa, T., & Ohta, T. (1989). Anharmonic interatomic potentials of 
metals and metal bromides determined by EXAFS. Japanese Journal of Applied 
Physics, 28(10), 1905-1908. https://doi.org/10.1143/JJAP.28.1905.