Nghiên cứu ảnh hưởng các yếu tố đến quá trình truyền sóng của đê giảm sóng kết cấu rỗng trên mô hình máng sóng

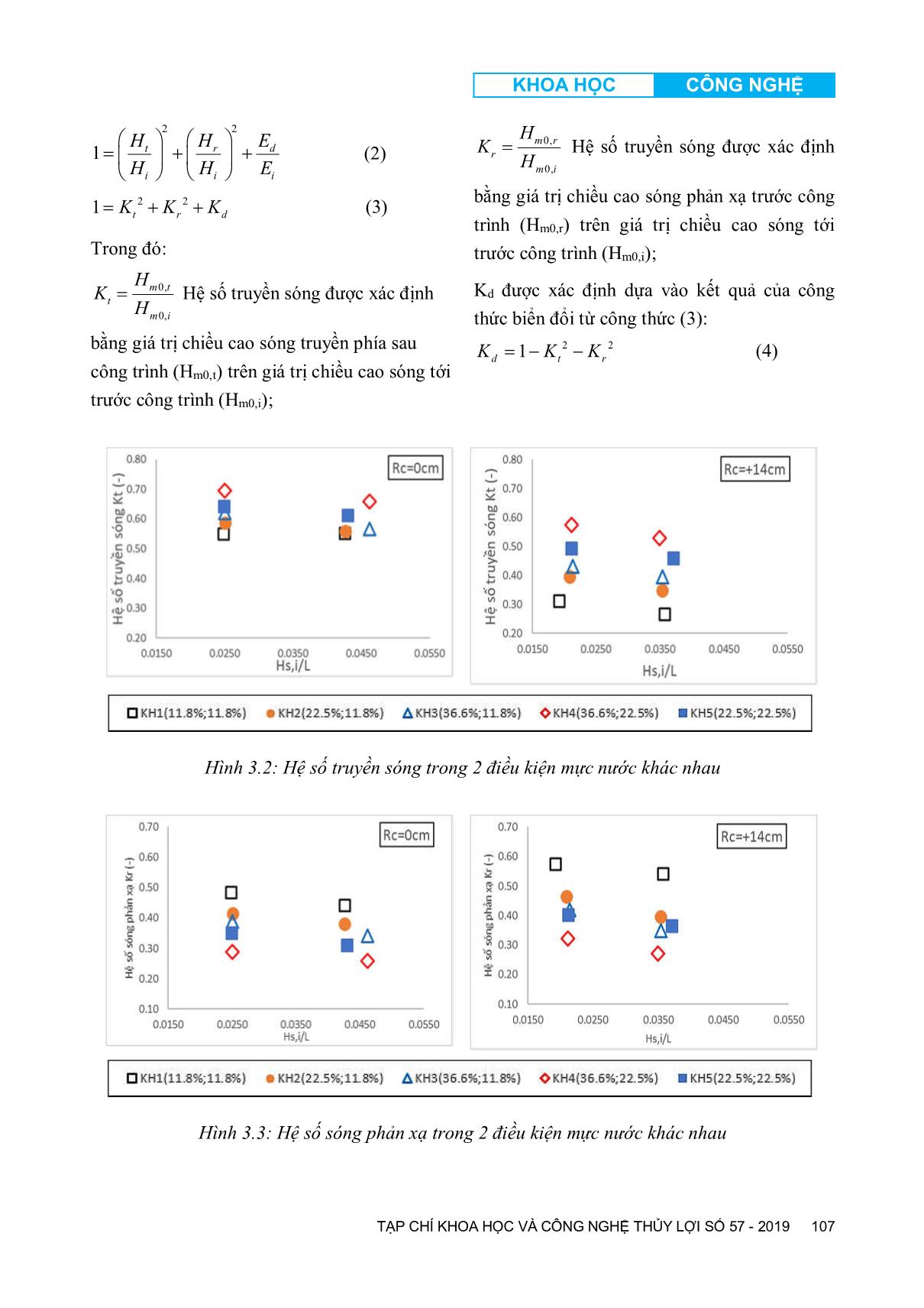
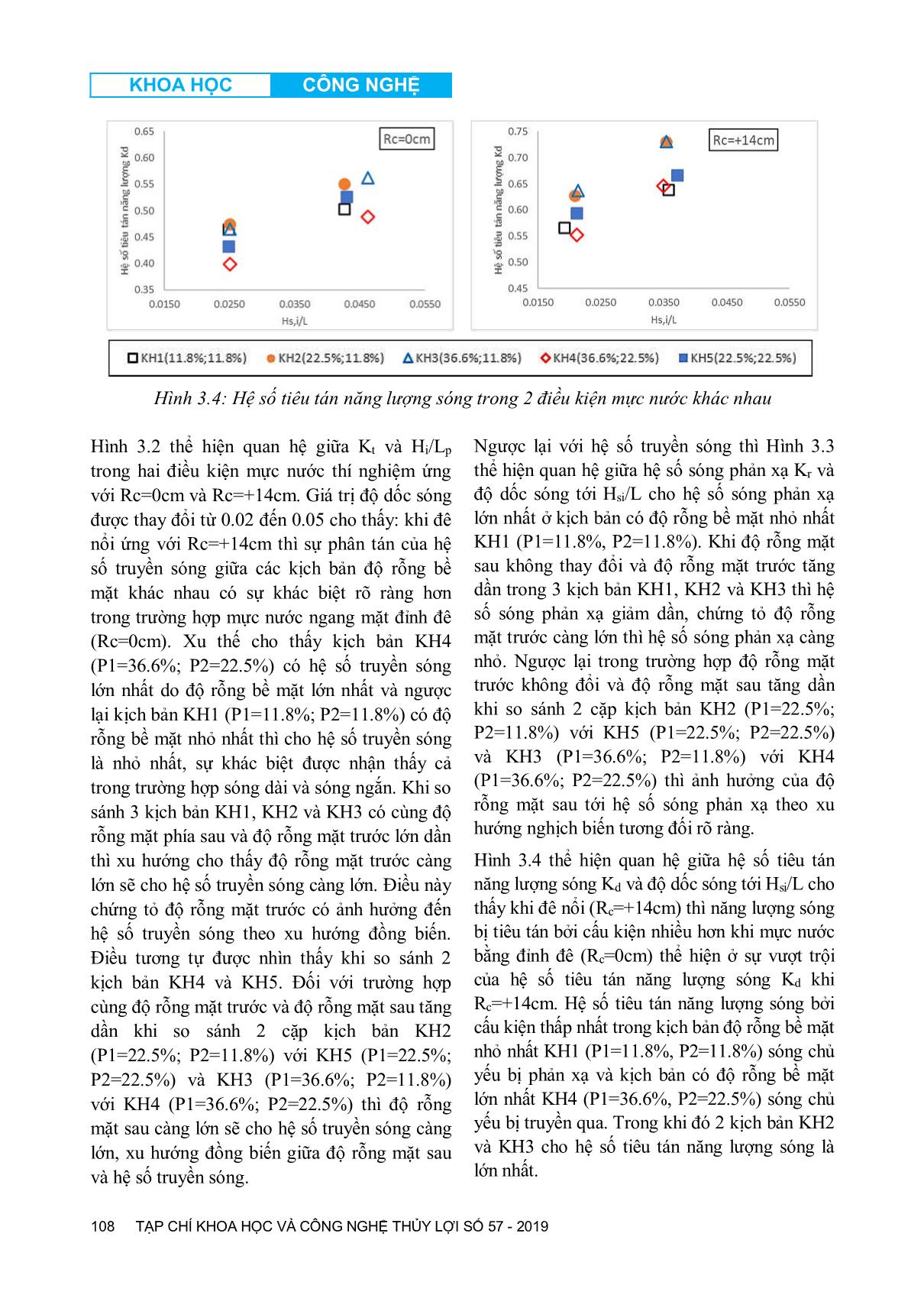
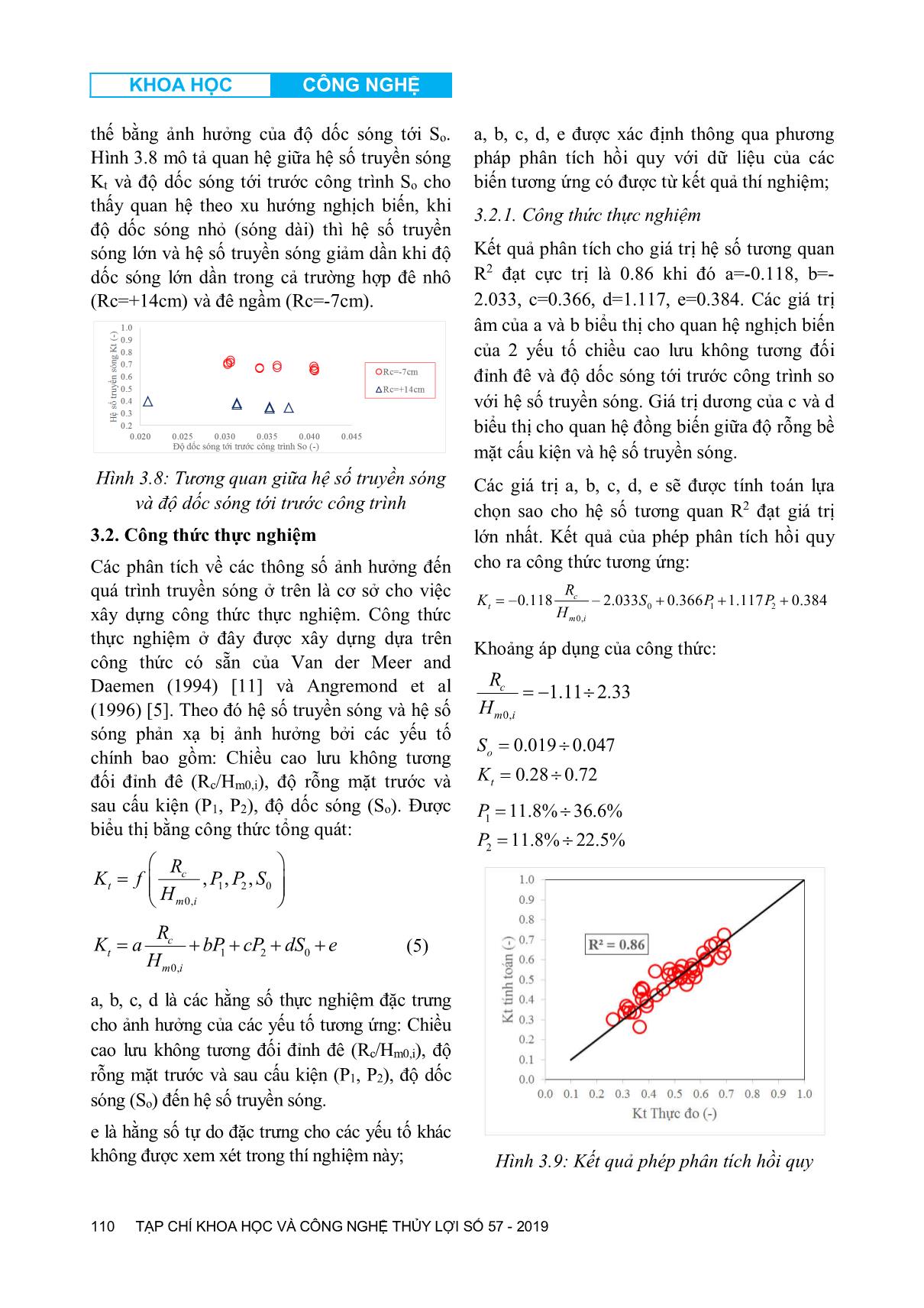
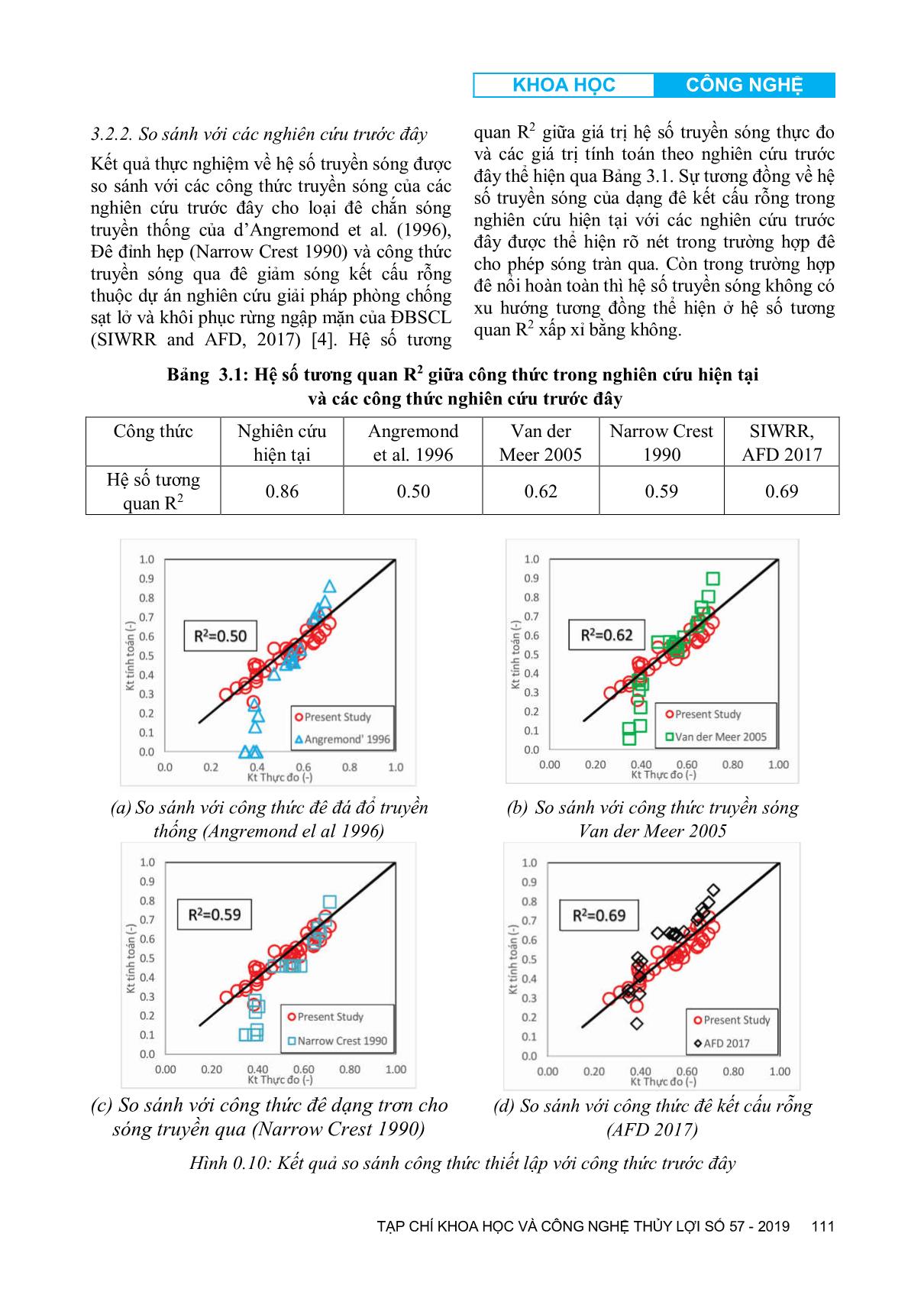
ết thì vấn đề thủy động 
lực học này tuân thủ định luật bảo toàn năng 
lượng và được thể hiện dưới dạng toán học 
băng công thức cân bằng năng lượng 
(Burcharth and Hughes 2003): 
i t r dE E E E (1) 
Trong đó, EI, Et, Er và Ed là năng lượng của 
sóng đến, sóng truyền, sóng phản xạ và sóng 
bị tiêu tán. Và hàm cân bằng năng lượng có 
thể được viết lại như sau: 
KHOA HỌC CÔNG NGHỆ 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 57 - 2019 107
2 2
1 t dr
i i i
H EH
H H E
(2) 
2 21 t r dK K K (3) 
Trong đó: 
0,
0,
m t
t
m i
H
K
H
 Hệ số truyền sóng được xác định 
bằng giá trị chiều cao sóng truyền phía sau 
công trình (Hm0,t) trên giá trị chiều cao sóng tới 
trước công trình (Hm0,i); 
0,
0,
m r
r
m i
H
K
H
 Hệ số truyền sóng được xác định 
bằng giá trị chiều cao sóng phản xạ trước công 
trình (Hm0,r) trên giá trị chiều cao sóng tới 
trước công trình (Hm0,i); 
Kd được xác định dựa vào kết quả của công 
thức biển đổi từ công thức (3): 
2 21d t rK K K (4) 
Hình 3.2: Hệ số truyền sóng trong 2 điều kiện mực nước khác nhau 
Hình 3.3: Hệ số sóng phản xạ trong 2 điều kiện mực nước khác nhau 
KHOA HỌC CÔNG NGHỆ 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 57 - 2019 108
Hình 3.4: Hệ số tiêu tán năng lượng sóng trong 2 điều kiện mực nước khác nhau 
Hình 3.2 thể hiện quan hệ giữa Kt và Hi/Lp 
trong hai điều kiện mực nước thí nghiệm ứng 
với Rc=0cm và Rc=+14cm. Giá trị độ dốc sóng 
được thay đổi từ 0.02 đến 0.05 cho thấy: khi đê 
nổi ứng với Rc=+14cm thì sự phân tán của hệ 
số truyền sóng giữa các kịch bản độ rỗng bề 
mặt khác nhau có sự khác biệt rõ ràng hơn 
trong trường hợp mực nước ngang mặt đỉnh đê 
(Rc=0cm). Xu thế cho thấy kịch bản KH4 
(P1=36.6%; P2=22.5%) có hệ số truyền sóng 
lớn nhất do độ rỗng bề mặt lớn nhất và ngược 
lại kịch bản KH1 (P1=11.8%; P2=11.8%) có độ 
rỗng bề mặt nhỏ nhất thì cho hệ số truyền sóng 
là nhỏ nhất, sự khác biệt được nhận thấy cả 
trong trường hợp sóng dài và sóng ngắn. Khi so 
sánh 3 kịch bản KH1, KH2 và KH3 có cùng độ 
rỗng mặt phía sau và độ rỗng mặt trước lớn dần 
thì xu hướng cho thấy độ rỗng mặt trước càng 
lớn sẽ cho hệ số truyền sóng càng lớn. Điều này 
chứng tỏ độ rỗng mặt trước có ảnh hưởng đến 
hệ số truyền sóng theo xu hướng đồng biến. 
Điều tương tự được nhìn thấy khi so sánh 2 
kịch bản KH4 và KH5. Đối với trường hợp 
cùng độ rỗng mặt trước và độ rỗng mặt sau tăng 
dần khi so sánh 2 cặp kịch bản KH2 
(P1=22.5%; P2=11.8%) với KH5 (P1=22.5%; 
P2=22.5%) và KH3 (P1=36.6%; P2=11.8%) 
với KH4 (P1=36.6%; P2=22.5%) thì độ rỗng 
mặt sau càng lớn sẽ cho hệ số truyền sóng càng 
lớn, xu hướng đồng biến giữa độ rỗng mặt sau 
và hệ số truyền sóng. 
Ngược lại với hệ số truyền sóng thì Hình 3.3 
thể hiện quan hệ giữa hệ số sóng phản xạ Kr và 
độ dốc sóng tới Hsi/L cho hệ số sóng phản xạ 
lớn nhất ở kịch bản có độ rỗng bề mặt nhỏ nhất 
KH1 (P1=11.8%, P2=11.8%). Khi độ rỗng mặt 
sau không thay đổi và độ rỗng mặt trước tăng 
dần trong 3 kịch bản KH1, KH2 và KH3 thì hệ 
số sóng phản xạ giảm dần, chứng tỏ độ rỗng 
mặt trước càng lớn thì hệ số sóng phản xạ càng 
nhỏ. Ngược lại trong trường hợp độ rỗng mặt 
trước không đổi và độ rỗng mặt sau tăng dần 
khi so sánh 2 cặp kịch bản KH2 (P1=22.5%; 
P2=11.8%) với KH5 (P1=22.5%; P2=22.5%) 
và KH3 (P1=36.6%; P2=11.8%) với KH4 
(P1=36.6%; P2=22.5%) thì ảnh hưởng của độ 
rỗng mặt sau tới hệ số sóng phản xạ theo xu 
hướng nghịch biến tương đối rõ ràng. 
Hình 3.4 thể hiện quan hệ giữa hệ số tiêu tán 
năng lượng sóng Kd và độ dốc sóng tới Hsi/L cho 
thấy khi đê nổi (Rc=+14cm) thì năng lượng sóng 
bị tiêu tán bởi cấu kiện nhiều hơn khi mực nước 
bằng đỉnh đê (Rc=0cm) thể hiện ở sự vượt trội 
của hệ số tiêu tán năng lượng sóng Kd khi 
Rc=+14cm. Hệ số tiêu tán năng lượng sóng bởi 
cấu kiện thấp nhất trong kịch bản độ rỗng bề mặt 
nhỏ nhất KH1 (P1=11.8%, P2=11.8%) sóng chủ 
yếu bị phản xạ và kịch bản có độ rỗng bề mặt 
lớn nhất KH4 (P1=36.6%, P2=22.5%) sóng chủ 
yếu bị truyền qua. Trong khi đó 2 kịch bản KH2 
và KH3 cho hệ số tiêu tán năng lượng sóng là 
lớn nhất. 
KHOA HỌC CÔNG NGHỆ 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 57 - 2019 109
3.1.2. Ảnh hưởng của chiều cao lưu không đỉnh đê 
- Hệ số truyền sóng 
Chiều cao lưu không tương đối của đỉnh để có 
ảnh hưởng rất rõ ràng đến hệ số lan truyền 
sóng Kt thể hiện trong Hình 3.5. Kết cấu công 
trình đạt hiệu quả giảm sóng cao trên 50% 
(ứng với hệ số truyền sóng kt nhỏ hơn 0.5) khi 
đê nổi (Rc>0cm). Hệ số truyền sóng bắt đầu có 
xu hướng không thay đổi nhiều khi Rc/Hm0,i > 
1.00 tức là khi sóng không tràn qua đỉnh đê mà 
chỉ truyền qua lỗ rỗng cấu kiện, lúc này hiệu 
quả giảm sóng của cấu kiện hoàn toàn phụ 
thuộc vào phần trăm lỗ rỗng hai mặt cấu kiện 
và hiệu quả giảm sóng đạt khoảng 66% tương 
ứng với hệ số truyền sóng kt= 0.34. 
Hình 3.5: Ảnh hưởng của chiều cao lưu 
 không đến hệ số truyền sóng 
- Hệ số sóng phản xạ 
Sóng phản xạ phía trước công trình được tạo 
thành từ tương tác giữa sóng và công trình. Nó 
không được mô tả chi tiết trong quá trình 
truyền sóng, tuy nhiên thông qua việc xác định 
hệ số sóng phản xạ cho phép xác định khả 
năng tiêu tán năng lượng sóng của công trình. 
Hình 3.6 thể hiện tương quan giữa hệ số sóng 
phản xạ Kr và chiều cao lưu không tương đối 
của đỉnh đê Rc/Hm0,i cho thấy khi Rc tăng dần 
từ -7cm đến 0cm (đê thay đổi từ trạng thái 
ngập qua mực nước bằng mặt đỉnh đê) thì hệ 
số sóng phản xạ cũng tăng theo xu hướng 
tuyến tính từ 0.28 lên 0.40. Khi đê làm việc 
trong điều kiện nổi Rc = +7cm tới Rc=+14cm 
thì hệ số sóng phản xạ không có xu hướng 
tăng giảm rõ ràng mà giao động trong khoảng 
từ 0.40 đến 0.45. 
Hình 3.6: Tương quan giữa hệ số sóng 
phản xạ và Rc/Hm0 
Điều kiện biên của thí nghiệm (Hs, Tp, Rc) 
được sử dụng để tính toán hệ số sóng phản xạ 
của đê dạng trơn, đê có khối phủ hấp thụ sóng 
dựa trên các công thức thực nghiệm được 
nghiên cứu bởi Zanuttigh and Van der Meer 
(2008) [9] thể hiện trong Hình 3.7. So với các 
dạng kết cấu đê giảm sóng nghiên cứu trước 
đây thì hệ số sóng phản xạ của kết cấu trong 
nghiên cứu này có xu hướng lớn hơn sóng 
phản xạ của dạng đê mái nghiêng có khối phủ 
hấp thụ sóng và nhỏ hơn đê dạng trơn không 
có khối phủ hấp thụ sóng. 
Việc nhận biết và tính toán sóng phản xạ rất 
cần thiết trong quá trình thiết kế đê giảm sóng 
kết cấu rỗng, đặc biệt cho việc thiết kế giải 
phải bảo vệ chân chống xói cho công trình. 
Hình 3.7: So sánh hệ số sóng phản xạ với các 
dạng kết cấu truyền thống 
3.1.3. Ảnh hưởng của độ dốc sóng tới trước 
công trình So 
Quá trình truyền sóng qua đê giảm sóng cũng 
phụ thuộc vào hiện tượng sóng vỡ trên mái của 
công trình, tương tác này được thể hiện qua 
chỉ số sóng vỡ Iribarren 0
0
tan
S

 Tuy nhiên 
độ dốc mái công trình 56o là một hằng số 
nên ảnh hưởng của chỉ số này có thể được thay 
KHOA HỌC CÔNG NGHỆ 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 57 - 2019 110
thế bằng ảnh hưởng của độ dốc sóng tới So. 
Hình 3.8 mô tả quan hệ giữa hệ số truyền sóng 
Kt và độ dốc sóng tới trước công trình So cho 
thấy quan hệ theo xu hướng nghịch biến, khi 
độ dốc sóng nhỏ (sóng dài) thì hệ số truyền 
sóng lớn và hệ số truyền sóng giảm dần khi độ 
dốc sóng lớn dần trong cả trường hợp đê nhô 
(Rc=+14cm) và đê ngầm (Rc=-7cm). 
Hình 3.8: Tương quan giữa hệ số truyền sóng 
và độ dốc sóng tới trước công trình 
3.2. Công thức thực nghiệm 
Các phân tích về các thông số ảnh hưởng đến 
quá trình truyền sóng ở trên là cơ sở cho việc 
xây dựng công thức thực nghiệm. Công thức 
thực nghiệm ở đây được xây dựng dựa trên 
công thức có sẵn của Van der Meer and 
Daemen (1994) [11] và Angremond et al 
(1996) [5]. Theo đó hệ số truyền sóng và hệ số 
sóng phản xạ bị ảnh hưởng bởi các yếu tố 
chính bao gồm: Chiều cao lưu không tương 
đối đỉnh đê (Rc/Hm0,i), độ rỗng mặt trước và 
sau cấu kiện (P1, P2), độ dốc sóng (So). Được 
biểu thị bằng công thức tổng quát: 
1 2 0
0,
, , ,ct
m i
R
K f P P S
H
1 2 0
0,
c
t
m i
R
K a bP cP dS e
H
(5) 
a, b, c, d là các hằng số thực nghiệm đặc trưng 
cho ảnh hưởng của các yếu tố tương ứng: Chiều 
cao lưu không tương đối đỉnh đê (Rc/Hm0,i), độ 
rỗng mặt trước và sau cấu kiện (P1, P2), độ dốc 
sóng (So) đến hệ số truyền sóng. 
e là hằng số tự do đặc trưng cho các yếu tố khác 
không được xem xét trong thí nghiệm này; 
a, b, c, d, e được xác định thông qua phương 
pháp phân tích hồi quy với dữ liệu của các 
biến tương ứng có được từ kết quả thí nghiệm; 
3.2.1. Công thức thực nghiệm 
Kết quả phân tích cho giá trị hệ số tương quan 
R2 đạt cực trị là 0.86 khi đó a=-0.118, b=-
2.033, c=0.366, d=1.117, e=0.384. Các giá trị 
âm của a và b biểu thị cho quan hệ nghịch biến 
của 2 yếu tố chiều cao lưu không tương đối 
đỉnh đê và độ dốc sóng tới trước công trình so 
với hệ số truyền sóng. Giá trị dương của c và d 
biểu thị cho quan hệ đồng biến giữa độ rỗng bề 
mặt cấu kiện và hệ số truyền sóng. 
Các giá trị a, b, c, d, e sẽ được tính toán lựa 
chọn sao cho hệ số tương quan R2 đạt giá trị 
lớn nhất. Kết quả của phép phân tích hồi quy 
cho ra công thức tương ứng: 
0 1 2
0,
0.118 2.033 0.366 1.117 0.384ct
m i
R
K S P P
H
Khoảng áp dụng của công thức: 
0,
1.11 2.33c
m i
R
H
  
0.019 0.047
0.28 0.72
o
t
S
K
 
 
1
2
11.8% 36.6%
11.8% 22.5%
P
P
 
 
Hình 3.9: Kết quả phép phân tích hồi quy 
KHOA HỌC CÔNG NGHỆ 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 57 - 2019 111
3.2.2. So sánh với các nghiên cứu trước đây 
Kết quả thực nghiệm về hệ số truyền sóng được 
so sánh với các công thức truyền sóng của các 
nghiên cứu trước đây cho loại đê chắn sóng 
truyền thống của d’Angremond et al. (1996), 
Đê đỉnh hẹp (Narrow Crest 1990) và công thức 
truyền sóng qua đê giảm sóng kết cấu rỗng 
thuộc dự án nghiên cứu giải pháp phòng chống 
sạt lở và khôi phục rừng ngập mặn của ĐBSCL 
(SIWRR and AFD, 2017) [4]. Hệ số tương 
quan R2 giữa giá trị hệ số truyền sóng thực đo 
và các giá trị tính toán theo nghiên cứu trước 
đây thể hiện qua Bảng 3.1. Sự tương đồng về hệ 
số truyền sóng của dạng đê kết cấu rỗng trong 
nghiên cứu hiện tại với các nghiên cứu trước 
đây được thể hiện rõ nét trong trường hợp đê 
cho phép sóng tràn qua. Còn trong trường hợp 
đê nổi hoàn toàn thì hệ số truyền sóng không có 
xu hướng tương đồng thể hiện ở hệ số tương 
quan R2 xấp xỉ bằng không. 
Bảng 3.1: Hệ số tương quan R2 giữa công thức trong nghiên cứu hiện tại 
 và các công thức nghiên cứu trước đây 
Công thức Nghiên cứu 
hiện tại 
Angremond 
et al. 1996 
Van der 
Meer 2005 
Narrow Crest 
1990 
SIWRR, 
AFD 2017 
Hệ số tương 
quan R2 
0.86 0.50 0.62 0.59 0.69 
(a) So sánh với công thức đê đá đổ truyền 
thống (Angremond el al 1996) 
(b) So sánh với công thức truyền sóng 
Van der Meer 2005 
(c) So sánh với công thức đê dạng trơn cho 
sóng truyền qua (Narrow Crest 1990) 
(d) So sánh với công thức đê kết cấu rỗng 
(AFD 2017) 
Hình 0.10: Kết quả so sánh công thức thiết lập với công thức trước đây 
KHOA HỌC CÔNG NGHỆ 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 57 - 2019 112
4. KẾT LUẬN VÀ KIẾN NGHỊ 
Chuỗi thí nghiệm đánh giá ảnh hưởng của độ 
rỗng bề mặt, chiều cao lưu không đỉnh đê và 
sự chi phối của các tham số sóng đến hiệu quả 
giảm sóng, các hệ số sóng phản xạ và hệ số 
tiêu tán năng lượng của kết cấu giảm sóng kết 
cấu rỗng đã được thực hiện trên mô hình vật lý 
2D của phòng thí nghiệm thủy động lực của 
Viện khoa học Thủy lợi miền Nam. Kết quả 
thí nghiệm cho một số kết luận: 
Độ rỗng bề mặt cấu kiện (bao gồm cả mặt 
trước và sau cấu kiện) ảnh hưởng đồng biến 
đến hệ số truyền sóng và nghịch biến với hệ số 
sóng phản xạ. 
Chiều cao lưu không tương đối đỉnh đê và độ 
dốc sóng ảnh hưởng nghịch biến đến hệ số 
truyền sóng. 
Từ kết quả số liệu thí nghiệm thực đo, nghiên 
cứu đã xây dựng được công thức xác định hệ 
số truyền sóng qua đê giảm sóng kết cấu rỗng. 
Công thức xác định hệ số truyền sóng bị chi 
phối bởi các yếu tố chính là chiều cao lưu 
không tương đối đỉnh đê (Rc/Hi), độ rỗng bề 
mặt (P1, P2), độ dốc sóng (S0). Sự tương đồng 
về hệ số truyền sóng giữa kết cấu trong nghiên 
cứu hiện tại với các kết cấu của những nghiên 
cứu trước đây xảy ra khi đê làm việc trong 
điều kiện cho phép sóng tràn qua. 
TÀI LIỆU THAM KHẢO 
[1] Hocine Oumeraci - Nonconventional Wave Damping Structures, Leichtweiss - Institute for 
hydraulic Engineering and water resource Technical University Braunschweig 
[2] Design of low-crested (submerged) structures - an overview - Krystian W. Pilarczyk, 
Rijkswaterstaat, Road and Hydraulic Engineering Division, P.O. Box 5044, 2600 GA 
Delft, the Netherlands; k.w.pilarczyk@dww.rws.minvenw.nl 
[3] Environmental Design of Low Crested Coastal Defence Structures “D31 Wave basin 
experiment final form-3D stability tests at AUU- by Morten kramer and Hans Burcharth”. 
[4] Report 2D laboratory study and protection measures for LWD wave transmission at porous 
breakwaters on mangrove foreshore and large-scale near-shore sandbank nourishment 
“AFD, SIWRR, European Union. 
[5] Angremond, K., Van der Meer, J.W. and de Jong, R.J., 1996. Wave transmission at 
low-crested structures. Proc. 25th ICCE, ASCE, Orlando, USA. 
[6] Implications for the concept of “bound” wave release at short wave breaking. 
Coastal Engineering, 60, pp. 276-285. 
[7] Horstman, E., Dohmen-Janssen, M., Narra, P., van den Berg, NJ., Siemerink, M., 
Balke, T., Bouma, T., and Hulscher, S., 2012. Wave attenuation in mangrove 
forests; field data obtained in Trang, Thailand. Proc. 33nd Int. Conf. Coastal Eng., 
ASCE , pp. 40. 
[8] Hughes, A.S., 1993. Physical models and laboratory techniques in coastal 
engineering, World Scientific, Singapore, 568 pp. 
[9] Zanuttigh, B., van der Meer, J.W. Wave reflection from coastal structures in design 
conditions. Coastal Engineering (55). 2008. pp. 771-779. 
[10] Tuan, T.Q., Tien, N.V. and Verhagen, H.J., 2016. Wave transmission over 
submerged, smooth and impermeable breakwaters on a gentle and shallow 
foreshore. In: Proc. 9th PIANC-COPEDEC, pp. 897-905, Rio de Janeiro, BRAZIL. 
KHOA HỌC CÔNG NGHỆ 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 57 - 2019 113
[11] Van der Meer, J.W., Daemen, I.F.R., 1994. Stability and wave transmission at low 
crested rubble mound structures. Journal of Waterway, Port Coastal and Ocean 
Engineering, 1, 1-19. 
[12] Van der Meer, J. W., Briganti, R., Zanuttigh, B. and Wang, B., 2005. Wave 
transmission and reflection at low-crested structures: Design formulae, oblique 
wave attack and spectral change. Coastal Engineering, 52, 915 - 929. 
[13] Zelt, J.A. and Skjelbreia, J.E., 1992. Estimating incident and reflected wave fields 
using an arbitrary number of wave gauges. Proc. 23rd Int. Conf. Coastal Eng., ASCE, 
pp. 777-789. 
[14] Wave reflection characteristics of permeable and impermeable submerged trapezoidal 
Breakwaters - Mathew Hornack (2011).