Một số mô hình phân loại học và đánh giá giáo dục trong việc đánh giá người học ngành Khoa học máy tính

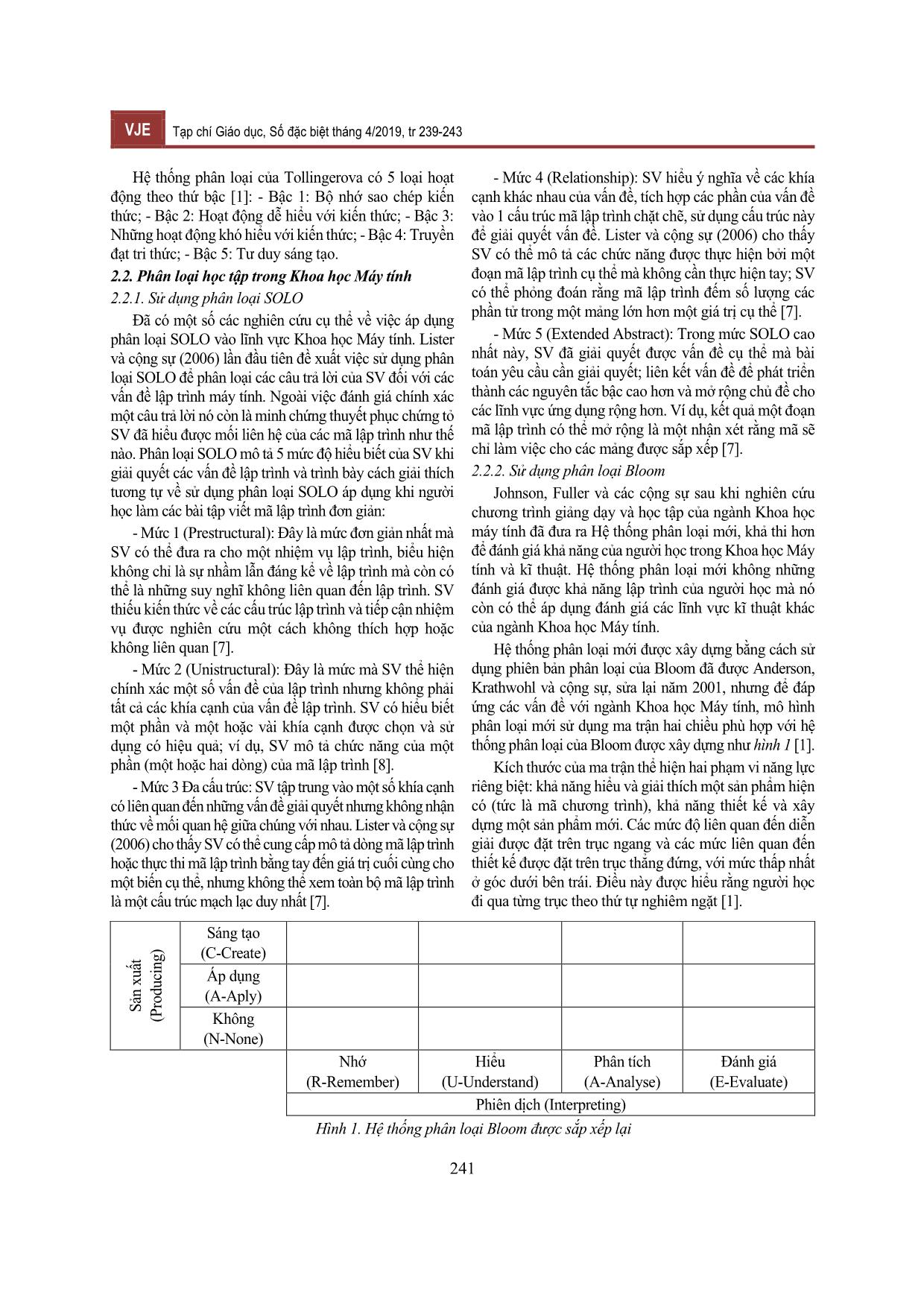
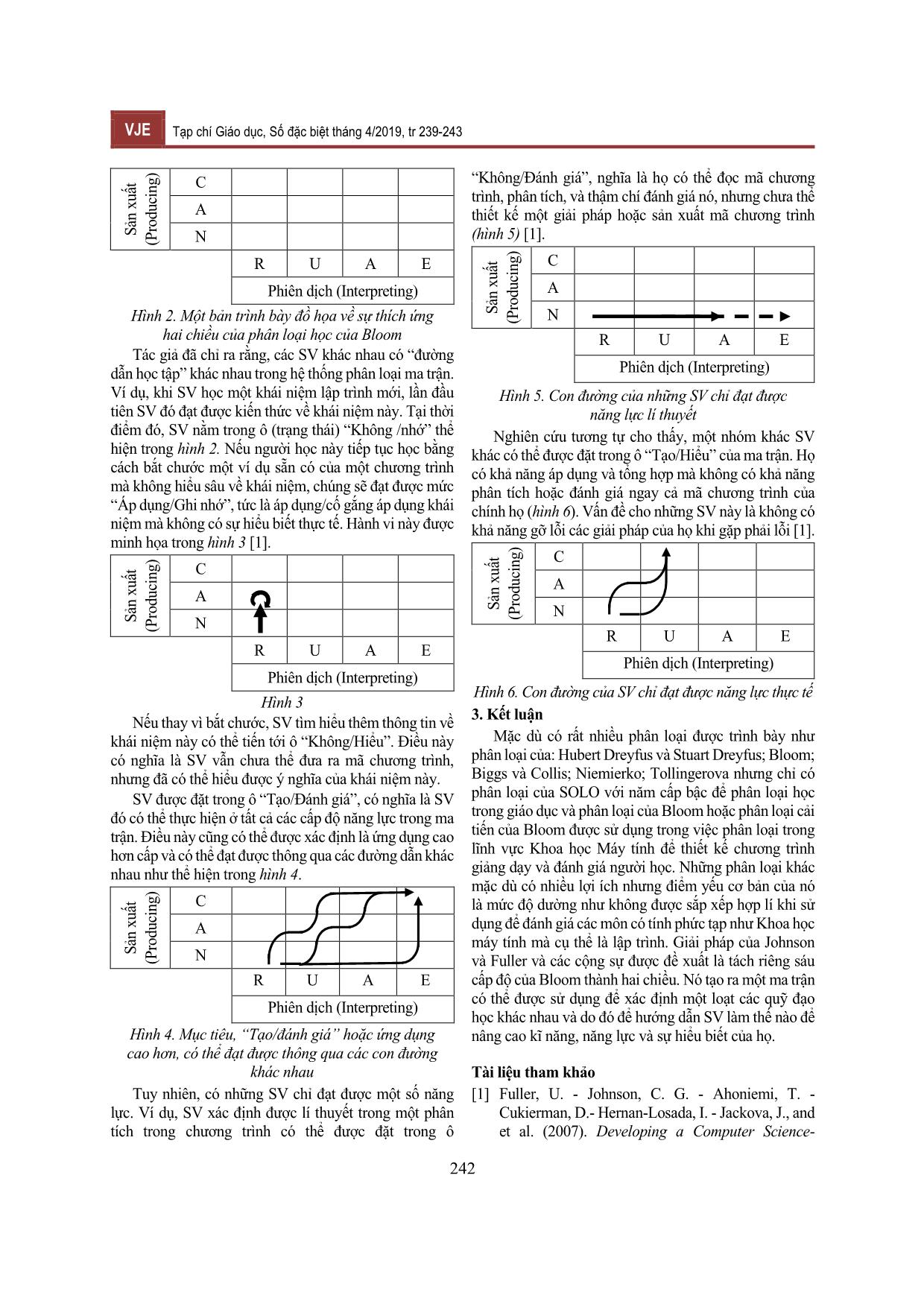
ơn cấu trúc (Uni-Structural): Câu trả lời 
chỉ dựa vào một khía cạnh liên quan, kết luận hạn chế và 
dễ mang tính giáo điều. 
- Mức 3: Đa cấu trúc (Multi-Structural): Một vài dữ 
liệu nhất quán được chọn lọc, bất cứ một sự không nhất 
quán hoặc nội dung trái chiều nào, đều được bỏ qua để 
có thể đưa ra kết luận chắc chắn. 
- Mức 4: Mối quan hệ (Relational): Hầu hết những 
dữ liệu được chấp nhận, những thông tin trái chiều được 
cho vào một hệ thống và giải thích trong một bối cảnh 
nhất định. 
- Mức 5: Trừu tượng mang tính mở (Extended 
Abstract): Người học có thể khái quát hóa cấu trúc để 
nắm bắt những vấn đề mới và trừu tượng hơn, biểu thị 
một trạng thái phát triển mới và cao hơn. 
Áp dụng Phân loại SOLO cho việc đánh giá kết quả 
học tập liên quan đến việc xem xét các mục tiêu của 
chuẩn đầu ra dự kiến ở các cấp độ khác nhau. Các tính 
năng quan trọng liên quan đến phân loại SOLO được 
trình bày bởi Biggs và Collis (1982) là phân loại SOLO 
phân cấp được người học và người học có xu hướng tiến 
bộ, các kết quả định lượng được thể hiện ở mức 2 và mức 
3; các kết quả định tính được thể hiện ở mức 4 và mức 5. 
Phân loại SOLO là nội dung độc lập và do đó nó có thể 
được sử dụng như một thước đo chung về sự hiểu biết 
giữa các ngành khác nhau. SOLO là một lược đồ phát 
triển phân loại các kết quả học tập theo độ phức tạp của 
chúng, do đó cho phép người hướng dẫn đánh giá công 
việc của sinh viên (SV) về chất lượng học tập chứ không 
phải là tính số lượng câu trả lời chính xác trong một 
nhiệm vụ hoặc hoạt động cụ thể [6]. 
2.1.4. Thang phân loại của Niemierko 
Niemierko và cộng sự cho rằng ba loại Bloom cao 
nhất (quy trình tư duy cao hơn) không thể được sắp xếp 
thứ bậc trong các môn khoa học. Ông đã phát triển hệ 
thống phân loại “ABC” của các mục tiêu học tập được tổ 
chức theo hai chiều (bảng 2): 
Bảng 2. Mức độ Các loại mục tiêu học tập 
Bậc Mục tiêu học tập 
I. Kiến thức 
A. Nhớ lại kiến thức 
B. Hiểu biết về kiến thức 
II. Khả năng 
và kĩ năng 
C. Áp dụng kiến thức trong các tình 
huống điển hình 
D. Ứng dụng kiến thức trong những 
tình huống phức tạp 
Các ứng dụng trong nhóm D bao gồm các phân tích, 
tổng hợp, và các loại đánh giá của hệ thống phân loại 
Bloom [1]. 
2.1.5. Thang phân loại của Tollingerova 
VJE Tạp chí Giáo dục, Số đặc biệt tháng 4/2019, tr 239-243 
241 
Hệ thống phân loại của Tollingerova có 5 loại hoạt 
động theo thứ bậc [1]: - Bậc 1: Bộ nhớ sao chép kiến 
thức; - Bậc 2: Hoạt động dễ hiểu với kiến thức; - Bậc 3: 
Những hoạt động khó hiểu với kiến thức; - Bậc 4: Truyền 
đạt tri thức; - Bậc 5: Tư duy sáng tạo. 
2.2. Phân loại học tập trong Khoa học Máy tính 
2.2.1. Sử dụng phân loại SOLO 
Đã có một số các nghiên cứu cụ thể về việc áp dụng 
phân loại SOLO vào lĩnh vực Khoa học Máy tính. Lister 
và cộng sự (2006) lần đầu tiên đề xuất việc sử dụng phân 
loại SOLO để phân loại các câu trả lời của SV đối với các 
vấn đề lập trình máy tính. Ngoài việc đánh giá chính xác 
một câu trả lời nó còn là minh chứng thuyết phục chứng tỏ 
SV đã hiểu được mối liên hệ của các mã lập trình như thế 
nào. Phân loại SOLO mô tả 5 mức độ hiểu biết của SV khi 
giải quyết các vấn đề lập trình và trình bày cách giải thích 
tương tự về sử dụng phân loại SOLO áp dụng khi người 
học làm các bài tập viết mã lập trình đơn giản: 
- Mức 1 (Prestructural): Đây là mức đơn giản nhất mà 
SV có thể đưa ra cho một nhiệm vụ lập trình, biểu hiện 
không chỉ là sự nhầm lẫn đáng kể về lập trình mà còn có 
thể là những suy nghĩ không liên quan đến lập trình. SV 
thiếu kiến thức về các cấu trúc lập trình và tiếp cận nhiệm 
vụ được nghiên cứu một cách không thích hợp hoặc 
không liên quan [7]. 
- Mức 2 (Unistructural): Đây là mức mà SV thể hiện 
chính xác một số vấn đề của lập trình nhưng không phải 
tất cả các khía cạnh của vấn đề lập trình. SV có hiểu biết 
một phần và một hoặc vài khía cạnh được chọn và sử 
dụng có hiệu quả; ví dụ, SV mô tả chức năng của một 
phần (một hoặc hai dòng) của mã lập trình [8]. 
- Mức 3 Đa cấu trúc: SV tập trung vào một số khía cạnh 
có liên quan đến những vấn đề giải quyết nhưng không nhận 
thức về mối quan hệ giữa chúng với nhau. Lister và cộng sự 
(2006) cho thấy SV có thể cung cấp mô tả dòng mã lập trình 
hoặc thực thi mã lập trình bằng tay đến giá trị cuối cùng cho 
một biến cụ thể, nhưng không thể xem toàn bộ mã lập trình 
là một cấu trúc mạch lạc duy nhất [7]. 
- Mức 4 (Relationship): SV hiểu ý nghĩa về các khía 
cạnh khác nhau của vấn đề, tích hợp các phần của vấn đề 
vào 1 cấu trúc mã lập trình chặt chẽ, sử dụng cấu trúc này 
để giải quyết vấn đề. Lister và cộng sự (2006) cho thấy 
SV có thể mô tả các chức năng được thực hiện bởi một 
đoạn mã lập trình cụ thể mà không cần thực hiện tay; SV 
có thể phỏng đoán rằng mã lập trình đếm số lượng các 
phần tử trong một mảng lớn hơn một giá trị cụ thể [7]. 
- Mức 5 (Extended Abstract): Trong mức SOLO cao 
nhất này, SV đã giải quyết được vấn đề cụ thể mà bài 
toán yêu cầu cần giải quyết; liên kết vấn đề để phát triển 
thành các nguyên tắc bậc cao hơn và mở rộng chủ đề cho 
các lĩnh vực ứng dụng rộng hơn. Ví dụ, kết quả một đoạn 
mã lập trình có thể mở rộng là một nhận xét rằng mã sẽ 
chỉ làm việc cho các mảng được sắp xếp [7]. 
2.2.2. Sử dụng phân loại Bloom 
Johnson, Fuller và các cộng sự sau khi nghiên cứu 
chương trình giảng dạy và học tập của ngành Khoa học 
máy tính đã đưa ra Hệ thống phân loại mới, khả thi hơn 
để đánh giá khả năng của người học trong Khoa học Máy 
tính và kĩ thuật. Hệ thống phân loại mới không những 
đánh giá được khả năng lập trình của người học mà nó 
còn có thể áp dụng đánh giá các lĩnh vực kĩ thuật khác 
của ngành Khoa học Máy tính. 
Hệ thống phân loại mới được xây dựng bằng cách sử 
dụng phiên bản phân loại của Bloom đã được Anderson, 
Krathwohl và cộng sự, sửa lại năm 2001, nhưng để đáp 
ứng các vấn đề với ngành Khoa học Máy tính, mô hình 
phân loại mới sử dụng ma trận hai chiều phù hợp với hệ 
thống phân loại của Bloom được xây dựng như hình 1 [1]. 
Kích thước của ma trận thể hiện hai phạm vi năng lực 
riêng biệt: khả năng hiểu và giải thích một sản phẩm hiện 
có (tức là mã chương trình), khả năng thiết kế và xây 
dựng một sản phẩm mới. Các mức độ liên quan đến diễn 
giải được đặt trên trục ngang và các mức liên quan đến 
thiết kế được đặt trên trục thẳng đứng, với mức thấp nhất 
ở góc dưới bên trái. Điều này được hiểu rằng người học 
đi qua từng trục theo thứ tự nghiêm ngặt [1]. 
S
ản
 x
u
ất
(P
ro
d
u
ci
n
g
) 
Sáng tạo 
(C-Create) 
Áp dụng 
(A-Aply) 
Không 
(N-None) 
Nhớ 
(R-Remember) 
Hiểu 
(U-Understand) 
Phân tích 
(A-Analyse) 
Đánh giá 
(E-Evaluate) 
 Phiên dịch (Interpreting) 
Hình 1. Hệ thống phân loại Bloom được sắp xếp lại 
VJE Tạp chí Giáo dục, Số đặc biệt tháng 4/2019, tr 239-243 
242 
S
ản
 x
u
ất
(P
ro
d
u
ci
n
g
) 
C 
A 
N 
 R U A E 
 Phiên dịch (Interpreting) 
Hình 2. Một bản trình bày đồ họa về sự thích ứng 
hai chiều của phân loại học của Bloom 
Tác giả đã chỉ ra rằng, các SV khác nhau có “đường 
dẫn học tập” khác nhau trong hệ thống phân loại ma trận. 
Ví dụ, khi SV học một khái niệm lập trình mới, lần đầu 
tiên SV đó đạt được kiến thức về khái niệm này. Tại thời 
điểm đó, SV nằm trong ô (trạng thái) “Không /nhớ” thể 
hiện trong hình 2. Nếu người học này tiếp tục học bằng 
cách bắt chước một ví dụ sẵn có của một chương trình 
mà không hiểu sâu về khái niệm, chúng sẽ đạt được mức 
“Áp dụng/Ghi nhớ”, tức là áp dụng/cố gắng áp dụng khái 
niệm mà không có sự hiểu biết thực tế. Hành vi này được 
minh họa trong hình 3 [1]. 
S
ản
 x
u
ất
(P
ro
d
u
ci
n
g
) 
C 
A 
N 
 R U A E 
 Phiên dịch (Interpreting) 
Hình 3 
Nếu thay vì bắt chước, SV tìm hiểu thêm thông tin về 
khái niệm này có thể tiến tới ô “Không/Hiểu”. Điều này 
có nghĩa là SV vẫn chưa thể đưa ra mã chương trình, 
nhưng đã có thể hiểu được ý nghĩa của khái niệm này. 
SV được đặt trong ô “Tạo/Đánh giá”, có nghĩa là SV 
đó có thể thực hiện ở tất cả các cấp độ năng lực trong ma 
trận. Điều này cũng có thể được xác định là ứng dụng cao 
hơn cấp và có thể đạt được thông qua các đường dẫn khác 
nhau như thể hiện trong hình 4. 
S
ản
 x
u
ất
(P
ro
d
u
ci
n
g
) 
C 
A 
N 
 R U A E 
 Phiên dịch (Interpreting) 
Hình 4. Mục tiêu, “Tạo/đánh giá” hoặc ứng dụng 
cao hơn, có thể đạt được thông qua các con đường 
khác nhau 
Tuy nhiên, có những SV chỉ đạt được một số năng 
lực. Ví dụ, SV xác định được lí thuyết trong một phân 
tích trong chương trình có thể được đặt trong ô 
“Không/Đánh giá”, nghĩa là họ có thể đọc mã chương 
trình, phân tích, và thậm chí đánh giá nó, nhưng chưa thể 
thiết kế một giải pháp hoặc sản xuất mã chương trình 
(hình 5) [1]. 
S
ản
 x
u
ất
(P
ro
d
u
ci
n
g
) 
C 
A 
N 
 R U A E 
 Phiên dịch (Interpreting) 
Hình 5. Con đường của những SV chỉ đạt được 
năng lực lí thuyết 
Nghiên cứu tương tự cho thấy, một nhóm khác SV 
khác có thể được đặt trong ô “Tạo/Hiểu” của ma trận. Họ 
có khả năng áp dụng và tổng hợp mà không có khả năng 
phân tích hoặc đánh giá ngay cả mã chương trình của 
chính họ (hình 6). Vấn đề cho những SV này là không có 
khả năng gỡ lỗi các giải pháp của họ khi gặp phải lỗi [1]. 
S
ản
 x
u
ất
(P
ro
d
u
ci
n
g
) 
C 
A 
N 
 R U A E 
 Phiên dịch (Interpreting) 
Hình 6. Con đường của SV chỉ đạt được năng lực thực tế 
3. Kết luận 
Mặc dù có rất nhiều phân loại được trình bày như 
phân loại của: Hubert Dreyfus và Stuart Dreyfus; Bloom; 
Biggs và Collis; Niemierko; Tollingerova nhưng chỉ có 
phân loại của SOLO với năm cấp bậc để phân loại học 
trong giáo dục và phân loại của Bloom hoặc phân loại cải 
tiến của Bloom được sử dụng trong việc phân loại trong 
lĩnh vực Khoa học Máy tính để thiết kế chương trình 
giảng dạy và đánh giá người học. Những phân loại khác 
mặc dù có nhiều lợi ích nhưng điểm yếu cơ bản của nó 
là mức độ dường như không được sắp xếp hợp lí khi sử 
dụng để đánh giá các môn có tính phức tạp như Khoa học 
máy tính mà cụ thể là lập trình. Giải pháp của Johnson 
và Fuller và các cộng sự được đề xuất là tách riêng sáu 
cấp độ của Bloom thành hai chiều. Nó tạo ra một ma trận 
có thể được sử dụng để xác định một loạt các quỹ đạo 
học khác nhau và do đó để hướng dẫn SV làm thế nào để 
nâng cao kĩ năng, năng lực và sự hiểu biết của họ. 
Tài liệu tham khảo 
[1] Fuller, U. - Johnson, C. G. - Ahoniemi, T. - 
Cukierman, D.- Hernan-Losada, I. - Jackova, J., and 
et al. (2007). Developing a Computer Science-
VJE Tạp chí Giáo dục, Số đặc biệt tháng 4/2019, tr 239-243 
243 
specific Learning Taxonomy. SIGCSE Bulletin, 
Vol. 39 (4), pp. 152-170. 
[2] Dreyfus, Stuart E. - Dreyfus, Hubert L. (1980). A 
Fiưe-Stage Model of the Mental Actiưities involved 
in Directed Skill Acquisition. Washington, DC: 
Storming Media. 
[3] Bloom, B. - Engelhart, M. - Furst, E. - Hill, W. - 
Krathwohl, D. (1956). Taxonomy of educational 
objectives: the classification of educational goals. 
Handbook 1: Cognitive Domain. Longmans Green, 
New York. 
[4] Nguyễn Lộc - Nguyễn Lan Phương (đồng chủ biên) 
- Đặng Xuân Cương - Trịnh Thị Anh Hoa - Nguyễn 
Thị Hồng Vân (2016). Phương pháp, kĩ thuật xây 
dựng chuẩn đánh giá năng lực đọc hiểu và năng lực 
giải quyết vấn đề. NXB Giáo dục Việt Nam. 
[5] Lâm Quang Thiệp (2011). Đo lường trong giáo dục lí 
thuyết và ứng dụng. NXB Đại học Quốc gia Hà Nội. 
[6] Biggs, J. B. - Collis, K. F. (1982). Evaluating the 
Quality of Learning: The SOLO Taxonomy. 
Academic Press, New York. 
[7] Chan, C. C. - Chui, M. S. - Chan, M. Y. C. (2002). 
Applying the Structure of the Observed Learning 
Outcomes (SOLO) taxonomy on student’s learning 
outcomes: An empirical study. Assessment & Evaluation 
in Higher Education, Vol. 27 (6), pp. 511-527. 
[8] Lister, R. - Simon, B. - Thompson, E. - Whalley, J. L. 
- Prasad, C. (2006). Not seeing the forest for the trees: 
novice programmers and the SOLO taxonomy. ACM 
SIGCSE Bulletin, Vol. 41 (3), pp. 118-122. 
[9] Lister, R. - Adams, E. S. - Fitzgerald, S. - Fone, W. 
- Hamer, J. - Lindholm, M. - McCartney, R. - 
Moström, E. - Sanders, K. - Seppälä, O. - Simon, B. 
- Thomas, L. (2004). A multi-national study of 
reading and tracing skills in novice programmers. 
ACM SIGCSE Bulletin, Vol. 36 (4), pp. 119-150. 
[10] Nguyễn Công Khanh (chủ biên) - Đào Thị Oanh 
(2017). Giáo trình Kiểm tra, đánh giá trong giáo 
dục. NXB Đại học Sư phạm. 
[11] Anderson, L. W. - Krathwohl, D. R. (2001). A 
Taxonomy for Learning, Teaching and Assessing: A 
Revision of Bloom’s Taxonomy of Educational 
Objectives. Addison Wesley Longman, New York, 
abridged edition. 
[12] Biggs, J. B. (1999). Teaching for Quality Learning 
at University. SRHE and Open University Press, 
Buckingham, UK. 
[13] Biggs, J. - Tang, C. (2007). Teaching for Quality 
Learning at University. SRHE and Open University 
Press, Maidenhead, UK, 3rd edition. 
[14] Brabrand, C. - Dahl, B. (2009). Using the SOLO 
Taxonomy to Analyze Competence Progression of 
University Science Curricula. Higher Education, 
Vol. 58 (4), pp. 531-549. 
RÈN LUYỆN NĂNG LỰC GIẢI QUYẾT VẤN ĐỀ... 
(Tiếp theo trang 183) 
đặt ra là tìm các thời điểm trong vòng 2 giây đầu tiên, con 
lắc ở vị trí có li độ dài bằng 1,5(cm), có nghĩa là tìm 
nghiệm [0;2]t của phương trình 
3
3cos(5 ) .
6 2
t
Đây là phương trình lượng giác cơ bản đối với hàm 
số cos (khi giải tìm nghiệm, HS cần lưu ý tới điều kiện 
của ẩn  0;2t ). 
3. Kết luận 
Trong dạy học môn Toán, NLGQVĐ là một trong 
những năng lực cơ bản của HS, giúp các em thành công 
trong học tập và trong cuộc sống; rèn luyện NLGQVĐ 
cho HS sẽ góp phần nâng cao hiệu quả dạy học môn 
Toán. Do vậy, trong quá trình dạy học môn Toán phần 
Lượng giác ở trường trung học phổ thông, GV cần vận 
dụng các phương pháp dạy học phù hợp với từng đối 
tượng HS nhằm giúp các em phát triển được NLGQVĐ. 
Tài liệu tham khảo 
[1] Bộ GD-ĐT (2018). Chương trình giáo dục phổ 
thông - chương trình tổng thể. 
[2] Bộ GD-ĐT (2018). Chương trình giáo dục phổ 
thông môn Toán. NXB Giáo dục Việt Nam. 
[3] Hoàng Phê (chủ biên, 1996). Từ điển Tiếng Việt. 
NXB Đà Nẵng. 
[4] Bộ GD-ĐT (2014). Tài liệu tập huấn PISA 2015 và 
dạng câu hỏi do OECD phát hành lĩnh vực Toán học. 
[5] Hoàng Ngọc Anh - Nguyễn Dương Hoàng - Nguyễn 
Tiến Trung (2017). Đổi mới quá trình dạy học môn 
Toán thông qua các chuyên đề dạy học. NXB Giáo 
dục Việt Nam. 
[6] Nguyễn Thị Lan Phương (2013). Khung đánh giá 
năng lực hiểu biết toán của PISA. Tạp chí Khoa học 
Giáo dục, Viện Khoa học Giáo dục Việt Nam. 
[7] G. Polya (1995). Toán học về những suy luận có lí. 
NXB Giáo dục. 
[8] K. K.Platonov (1997). Tâm lí học. NXB Đại học Sư phạm. 
[9] Nguyễn Bá Kim (chủ biên) - Vũ Dương Thụy (1992). 
Phương pháp dạy học môn Toán. NXB Giáo dục. 
[10] Phạm Gia Đức (1998). Phương pháp dạy học môn 
Toán (tập 1). NXB Giáo dục.