Một phương pháp định lượng giá trị ngôn ngữ cho tập mẫu huấn luyện trong điều kiện hạn chế

ất LươngTháng trong 
Bảng 2 như sau: XLươngTháng = ( XLươngTháng, GLươngTháng, HLươngTháng, ), với GLươngTháng = {cao, thấp}, 
 40 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 14, Số 1 (2019) 
H+LươngTháng = ,hơn, rất}, H-LươngTháng = {khả năng, ít} với quan hệ ngữ nghĩa: rất > hơn và ít 
>khả năng. WLươngTháng = 0.6, fm(thấp) = 0.4, fm(cao) = 0.6, fm(rất) = 0.35, fm(hơn) = 0.25, 
fm(khả năng) = 0.20, fm(ít) = 0.20. Miền trị ngôn ngữ là {Ít cao, Thấp, Khả năng cao, Ít thấp, 
Cao, Cao, Rất cao, Ít thấp, Rất cao, Khả năng cao, Rất cao, Ít thấp, Khả năng cao, Khả năng 
cao}. IC() = {0.45, 0.24, 0.52, 0.34, 0.64, 0.64, 0.79, 0.35, 1, 0.50, 0.79, 0.4, 0.55, 0.50}. Biết 
đoạn con có miền trị là *1, 2] = [30, 65+ tương ứng với miền trị của ngôn ngữ là *LV1, 
LV2] = [Ít thấp, Hơn cao+. Hãy định lượng các giá trị ngôn ngữ cho LươngTháng. 
 Ta có: fm(rất thấp) = 0.35 x 0.4 = 0.14, fm(hơn thấp) = 025 x 0.4 = 0.10, fm(ít thấp) = 
0.2 x 0.4 = 0.08, fm(khả năng thấp) = 0.2 x 0.4 = 0.08. Vì rất thấp < hơn thấp < thấp < khả năng 
thấp < ít thấp nên: I(rất thấp) = [0, 0.14], I(hơn thấp) = [0.14, 0.24], I(khả năng thấp) = [0.24, 
0.32], I(ít thấp) = [0.32, 0.4]. fm(rất cao) = 0.35 x 0.6 = 0.21, fm(hơn cao) = 0.25 x 0.6 = 0.15, 
fm(ít cao) = 0.2 x 0.6 = 0.12, fm(khả năng cao) = 0.2 x 0.6 = 0.12. Vì ít cao < khả năng cao < 
cao < hơn cao < rất cao nên : I(ít cao) = [0.4, 0.52], I(khả năng cao) = [0.52, 0.64], I(hơn cao) = 
[0.64, 0.79], I(rất cao) = [0.79, 1]. 
 B1: Tính các  có giá trị ngôn ngữ trong đoạn [Ít thấp, Hơn cao] 
 Ít thấp = IC(Ít cao)(2-1)+1 = 0.4(65-30)+30=44 
 Ít cao = IC(Ít cao)(2-1)+1 = 0.52(65-30)+30=48 
 Khả năng cao = IC(Khả năng cao)(2-1)+1 = 0.64(65-30)+30=52 
 B2: Tính các  có giá trị ngôn ngữ trong đoạn [Hơn cao, Rất cao] 
 Hơn cao = 2*IC(Khả năng cao)/IC(Hơn cao) = 65 * 0.64 / 0.52 = 80 
 Rất cao = 2*IC(Hơn cao)/IC(Rấ cao) = 80 * 0.79 / 0.64 = 99 
 B3: Tính các  có giá trị ngôn ngữ trong đoạn [Rất thấp, Ít thấp] 
 Khả năng thấp = 1*IC(Ít thấp)/IC(Khả năng thấp) = 30 * 0.32 / 0.4 = 24 
 Hơn thấp = 1*IC(Khả năng thấp)/IC(Hơn thấp) = 24 * 0.24 / 0.32 = 18 
 Rất thấp = 1*IC(Hơn thấp)/IC(Rất thấp) = 18 * 0.14 / 0.24 = 10 
 Vậy miền trị sau khi được định lượng giá trị là: {48, 18, 52, 30, 80, 80, 99, 30, 99, 
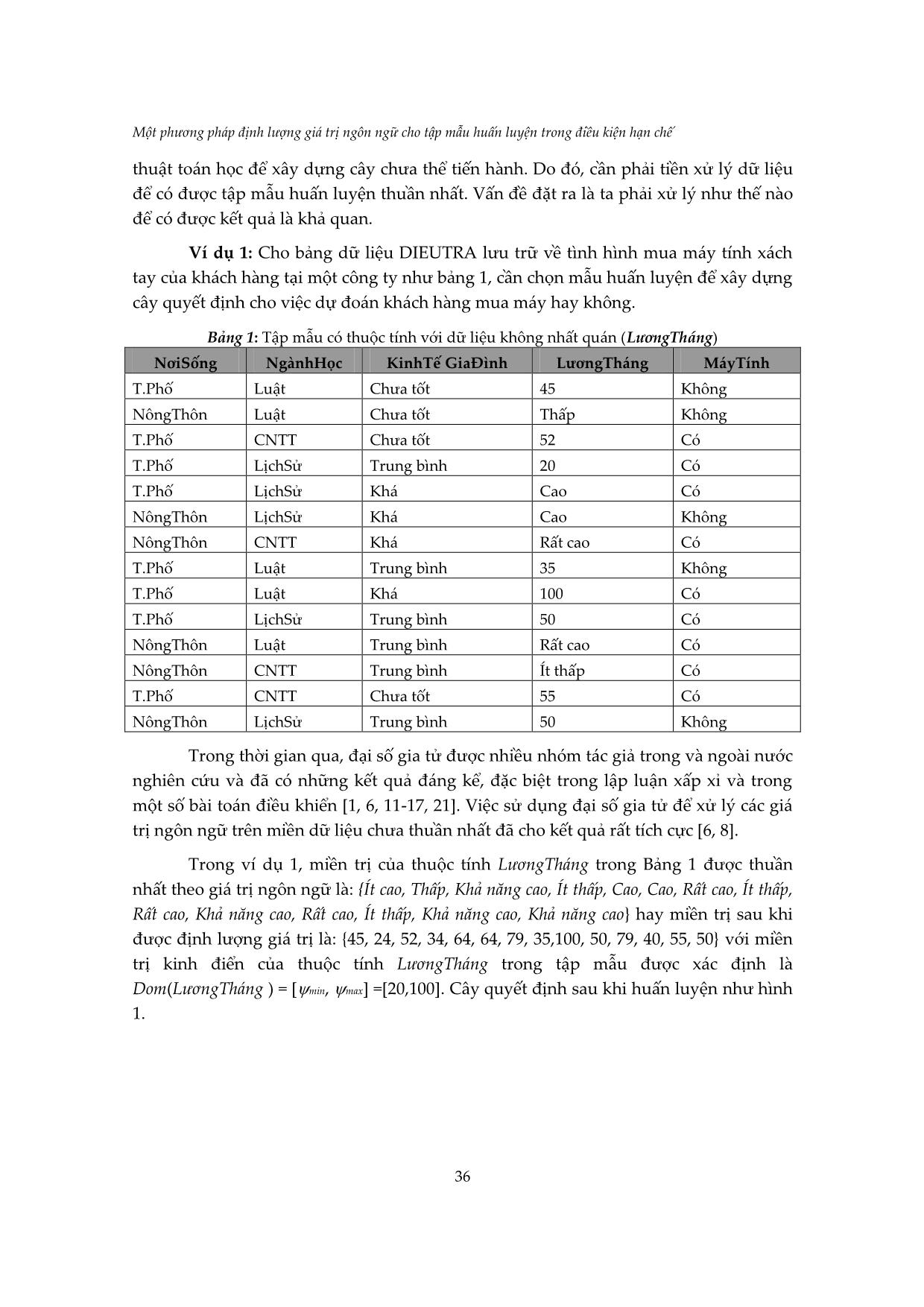
52, 99, 30, 52, 52}. Cây quyết định sau khi huấn luyện như hình 2. 
 41 
Một phương pháp định lượng giá trị ngôn ngữ cho tập mẫu huấn luyện trong điều kiện hạn chế 
 Ngànhhọc 
 Luật LịchSử 
 CNTT 
 Lƣơng tháng Có Nơi sống 
 >=80 <80 Nông thôn T.Phố 
 Không Có 
 Có Không 
 Hình 2. Cây quyết định được tạo sau khi định lượng thuộc tính nhờ biết đoạn con 
 của [min, max] và toàn bộ IC() 
2. Định lƣợng giá trị ngôn ngữ khi chỉ biết một đoạn con của [min, max] nhƣng chƣa 
xác định đƣợc toàn bộ IC() 
 Cho thuộc tính không thuần nhất Ai, lúc này ta có Dom(Ai) = DAi LDAi nhưng 
giá trị biên *min, max+ đối với miền trị kinh điển DAi của Ai không được xác định, mà ta 
cũng chỉ tìm được một đoạn con *1, 2] của nó tương ứng giá trị ngôn ngữ *LV1, LV2] 
của LDAi tức là (LV1) = IC(1) và (LV2) = IC(2). Lúc này ta phải tìm các giá trị IC(i) 
còn lại tức các IC(i) thỏa IC(i) IC(2) 
  
 1 max
 Do IC() = nên tất cả các  nằm giữa [1, 2+ sẽ đúng với quy tắc 
 max min
  
 2 
này, tức là IC() = 1 với  21 . Do vậy có thể xây dựng một ĐSGT để 
 2 1
định lượng giá trị cho chúng. 
 Theo phương pháp xây dựng ĐSGT đã nêu ở mục II, ta thấy tính mờ của các 
giá trị trong đại số gia tử là một đoạn con của *0,1+ cho nên họ các đoạn con như vậy 
của các giá trị có cùng độ dài sẽ tạo thành phân hoạch của *0,1+. Phân hoạch ứng với 
các giá trị có độ dài từ lớn hơn sẽ mịn hơn và khi độ dài lớn vô hạn thì độ dài của các 
đoạn trong phân hoạch giảm dần về 0. 
 Hơn nữa, các giá trị ngôn ngữ là một tập sắp thứ tự tuyến tính nên ta sẽ chia 
các đoạn con tương ứng thành các phân hoạch nhỏ hơn nhằm xác định lại độ dài của 
các đoạn *0, (i)] hay [(i), 1+ để từ đó có xác định giá trị rõ cho các giá trị ngôn ngữ 
này. Đây chính là điểm để tính các IC() không nằm trong đoạn *1, 2] bằng cách 
phân chia liên tiếp các đoạn con này để xác định các IC(i) tương ứng. Vậy ta có giải 
thuật như sau 
 B1: Xây dựng 1 ĐSGT trong miền *1, 2+ để tính các IC() tương ứng cho các 
giá trị trong đoạn *1, 2] này. 
 42 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 14, Số 1 (2019) 
 B2: Tính lại các phân hoạch cho các IC() như sau : 
 1. Nếu i < 1 thì : 
 - Phân hoạch đoạn [0, (1)] thành [0, (i)] và [(i), (1)] 
 - Tính fm(hi) ~ fm(h1) x I(1) và fm(h1) = fm(h1) - fm(hi) 
 2. Nếu i > 2 thì : 
 - Phân hoạch đoạn *(2), 1] thành [(2), (i)] và [(i), 1] 
 - Tính fm(hi) ~ fm(h2) x I(2) và fm(h2) = fm(h2) - fm(hi) 
 3. Tính giá trị IC(i) và i tại vị trí i. Gán vị trí i đang có thành vị trí 1 và tiếp tục 
tính lùi với các giá trị còn lại với i < 1 hay gán vị trí i đang có thành vị trí 2 và tiếp tục 
tính tiến với các giá trị còn lại với i > 2 
 B3: Thực hiện định lượng các giá trị ngôn ngữ với cách tính ở mục 1 khi đã biết 
toàn bộ IC(). 
 Tính đúng của giải thuật: Do tất cả các phân hoạch trên không vượt ra khỏi đoạn 
đang xét là |fm(h1)| hay |fm(h2| nên không làm phá vỡ các phân hoạch đang có của 
đoạn *0,1+, do I(1)>0 và I(2)<1, nên cách phân hoạch trên là phù hợp với phương 
pháp thuần nhất đã nêu ở mục II. 
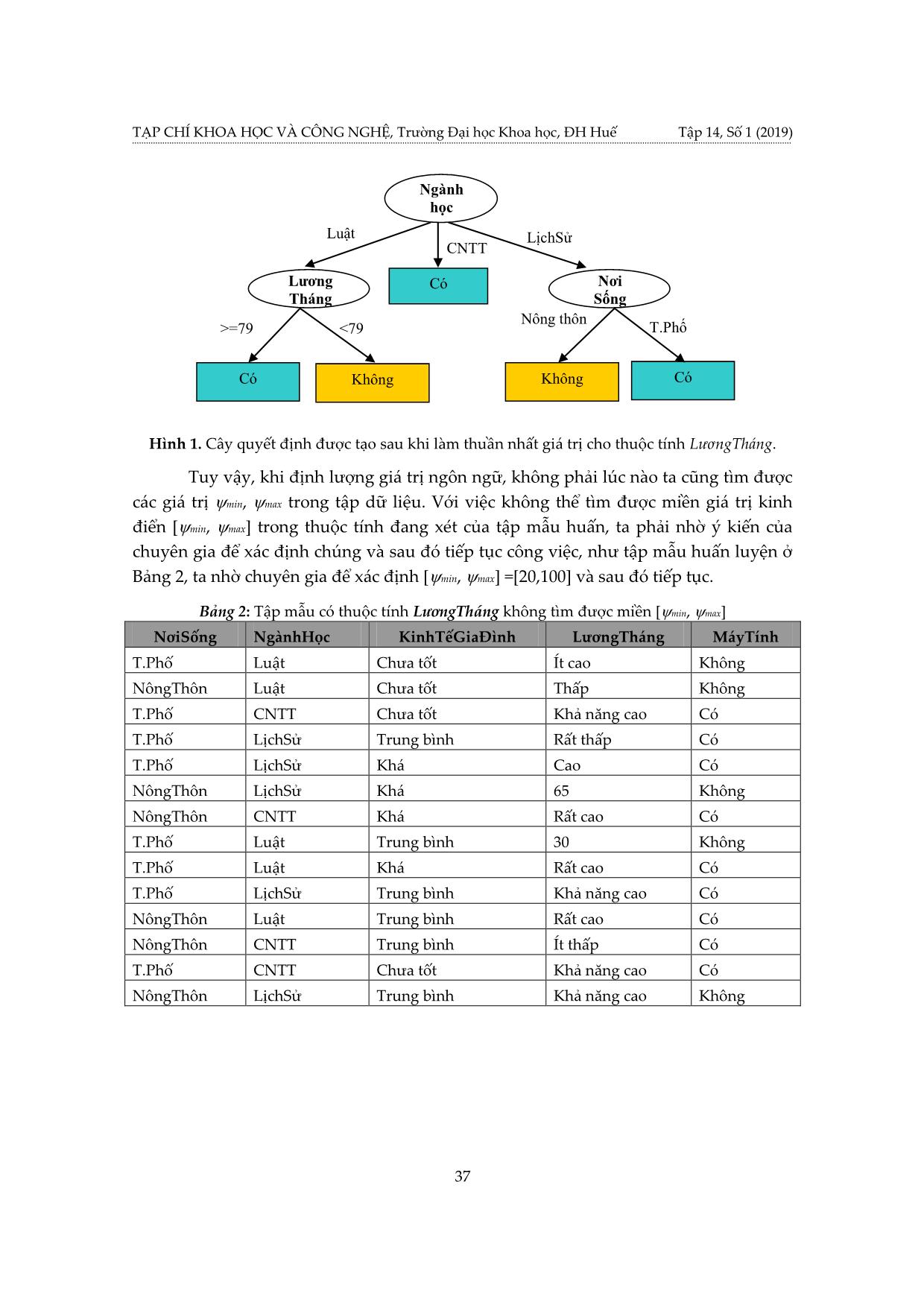
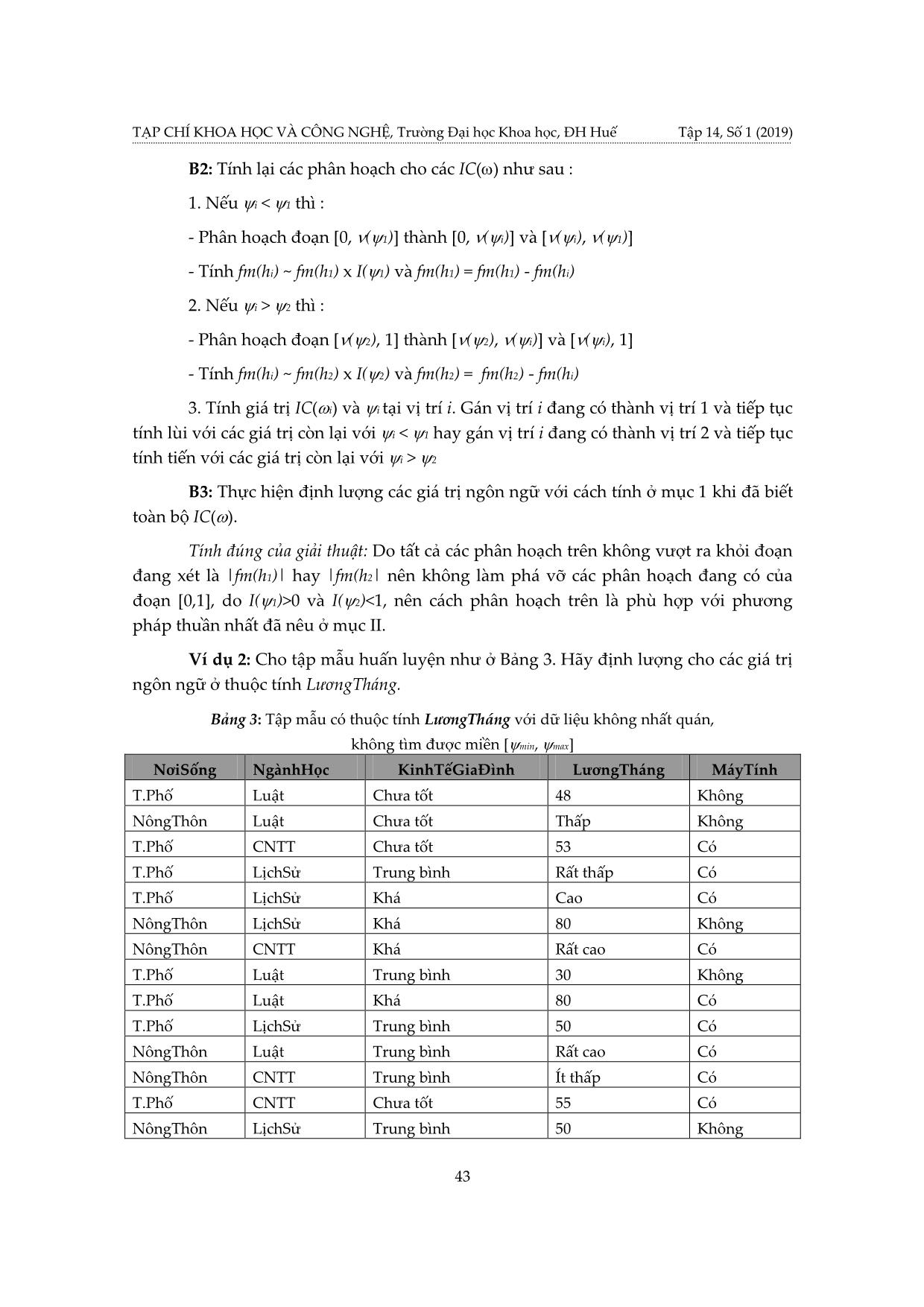
 Ví dụ 2: Cho tập mẫu huấn luyện như ở Bảng 3. Hãy định lượng cho các giá trị 
ngôn ngữ ở thuộc tính LươngTháng. 
 Bảng 3: Tập mẫu có thuộc tính LươngTháng với dữ liệu không nhất quán, 
 không tìm được miền [min, max] 
 NơiSống NgànhHọc KinhTếGiaĐình LƣơngTháng MáyTính 
T.Phố Luật Chưa tốt 48 Không 
NôngThôn Luật Chưa tốt Thấp Không 
T.Phố CNTT Chưa tốt 53 Có 
T.Phố LịchSử Trung bình Rất thấp Có 
T.Phố LịchSử Khá Cao Có 
NôngThôn LịchSử Khá 80 Không 
NôngThôn CNTT Khá Rất cao Có 
T.Phố Luật Trung bình 30 Không 
T.Phố Luật Khá 80 Có 
T.Phố LịchSử Trung bình 50 Có 
NôngThôn Luật Trung bình Rất cao Có 
NôngThôn CNTT Trung bình Ít thấp Có 
T.Phố CNTT Chưa tốt 55 Có 
NôngThôn LịchSử Trung bình 50 Không 
 43 
Một phương pháp định lượng giá trị ngôn ngữ cho tập mẫu huấn luyện trong điều kiện hạn chế 
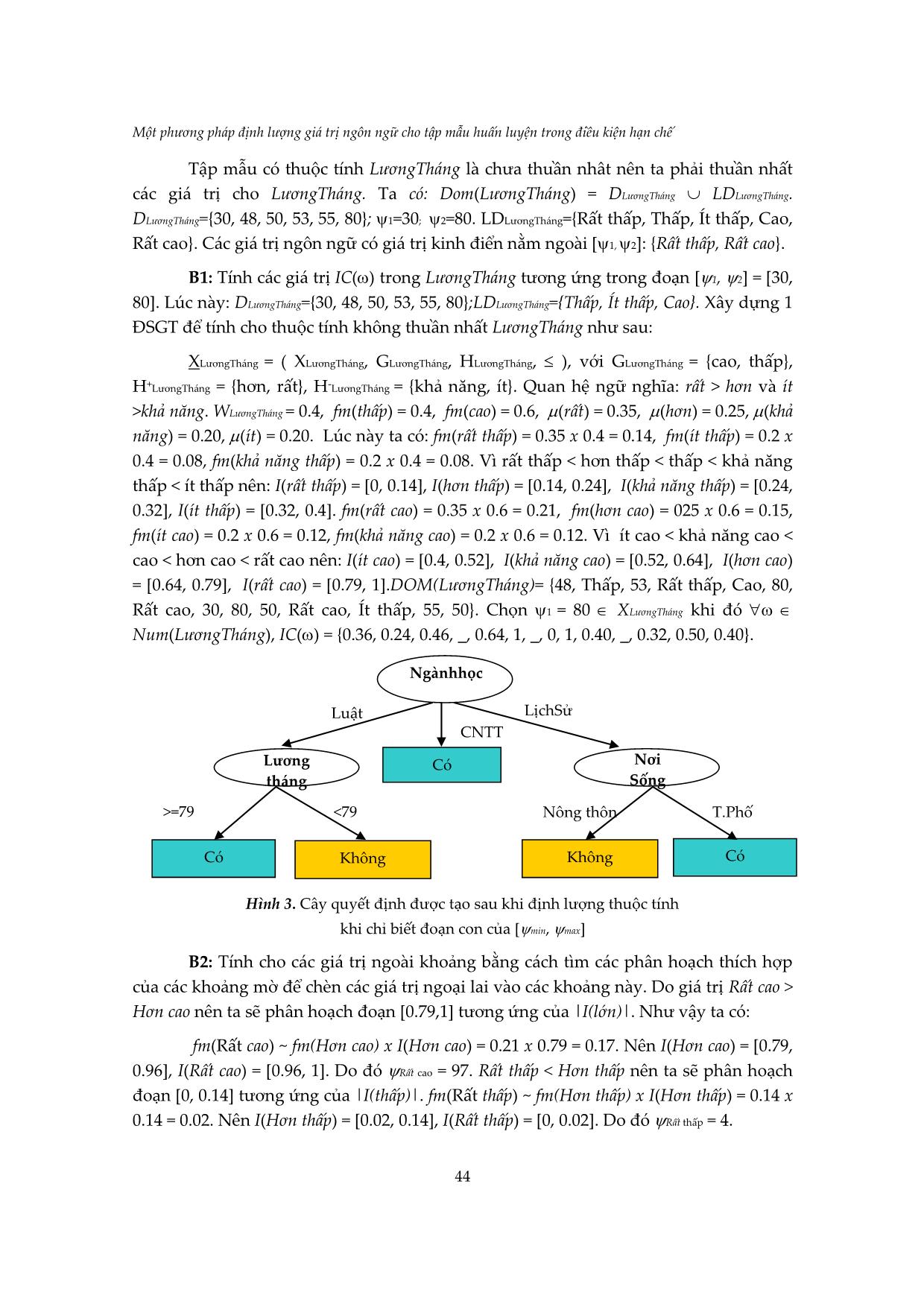
 Tập mẫu có thuộc tính LươngTháng là chưa thuần nhât nên ta phải thuần nhất 
các giá trị cho LươngTháng. Ta có: Dom(LươngTháng) = DLươngTháng  LDLươngTháng. 
DLươngTháng={30, 48, 50, 53, 55, 80}; 1=30; 2=80. LDLươngTháng=,Rất thấp, Thấp, Ít thấp, Cao, 
Rất cao}. Các giá trị ngôn ngữ có giá trị kinh điển nằm ngoài *1, 2]: {Rất thấp, Rất cao}. 
 B1: Tính các giá trị IC() trong LươngTháng tương ứng trong đoạn [1, 2] = [30, 
80]. Lúc này: DLươngTháng={30, 48, 50, 53, 55, 80};LDLươngTháng={Thấp, Ít thấp, Cao}. Xây dựng 1 
ĐSGT để tính cho thuộc tính không thuần nhất LươngTháng như sau: 
 XLươngTháng = ( XLươngTháng, GLươngTháng, HLươngTháng, ), với GLươngTháng = {cao, thấp}, 
H+LươngTháng = ,hơn, rất}, H-LươngTháng = {khả năng, ít}. Quan hệ ngữ nghĩa: rất > hơn và ít 
>khả năng. WLươngTháng = 0.4, fm(thấp) = 0.4, fm(cao) = 0.6, (rất) = 0.35, (hơn) = 0.25, (khả 
năng) = 0.20, (ít) = 0.20. Lúc này ta có: fm(rất thấp) = 0.35 x 0.4 = 0.14, fm(ít thấp) = 0.2 x 
0.4 = 0.08, fm(khả năng thấp) = 0.2 x 0.4 = 0.08. Vì rất thấp < hơn thấp < thấp < khả năng 
thấp < ít thấp nên: I(rất thấp) = [0, 0.14], I(hơn thấp) = [0.14, 0.24], I(khả năng thấp) = [0.24, 
0.32], I(ít thấp) = [0.32, 0.4]. fm(rất cao) = 0.35 x 0.6 = 0.21, fm(hơn cao) = 025 x 0.6 = 0.15, 
fm(ít cao) = 0.2 x 0.6 = 0.12, fm(khả năng cao) = 0.2 x 0.6 = 0.12. Vì ít cao < khả năng cao < 
cao < hơn cao < rất cao nên: I(ít cao) = [0.4, 0.52], I(khả năng cao) = [0.52, 0.64], I(hơn cao) 
= [0.64, 0.79], I(rất cao) = [0.79, 1].DOM(LươngTháng)= ,48, Thấp, 53, Rất thấp, Cao, 80, 
Rất cao, 30, 80, 50, Rất cao, Ít thấp, 55, 50}. Chọn 1 = 80 XLươngTháng khi đó  
Num(LươngTháng), IC() = {0.36, 0.24, 0.46, _, 0.64, 1, _, 0, 1, 0.40, _, 0.32, 0.50, 0.40}. 
 Ngànhhọc 
 Luật LịchSử 
 CNTT 
 Lƣơng Có Nơi 
 tháng Sống 
 >=79 <79 Nông thôn T.Phố 
 Có Không Không Có 
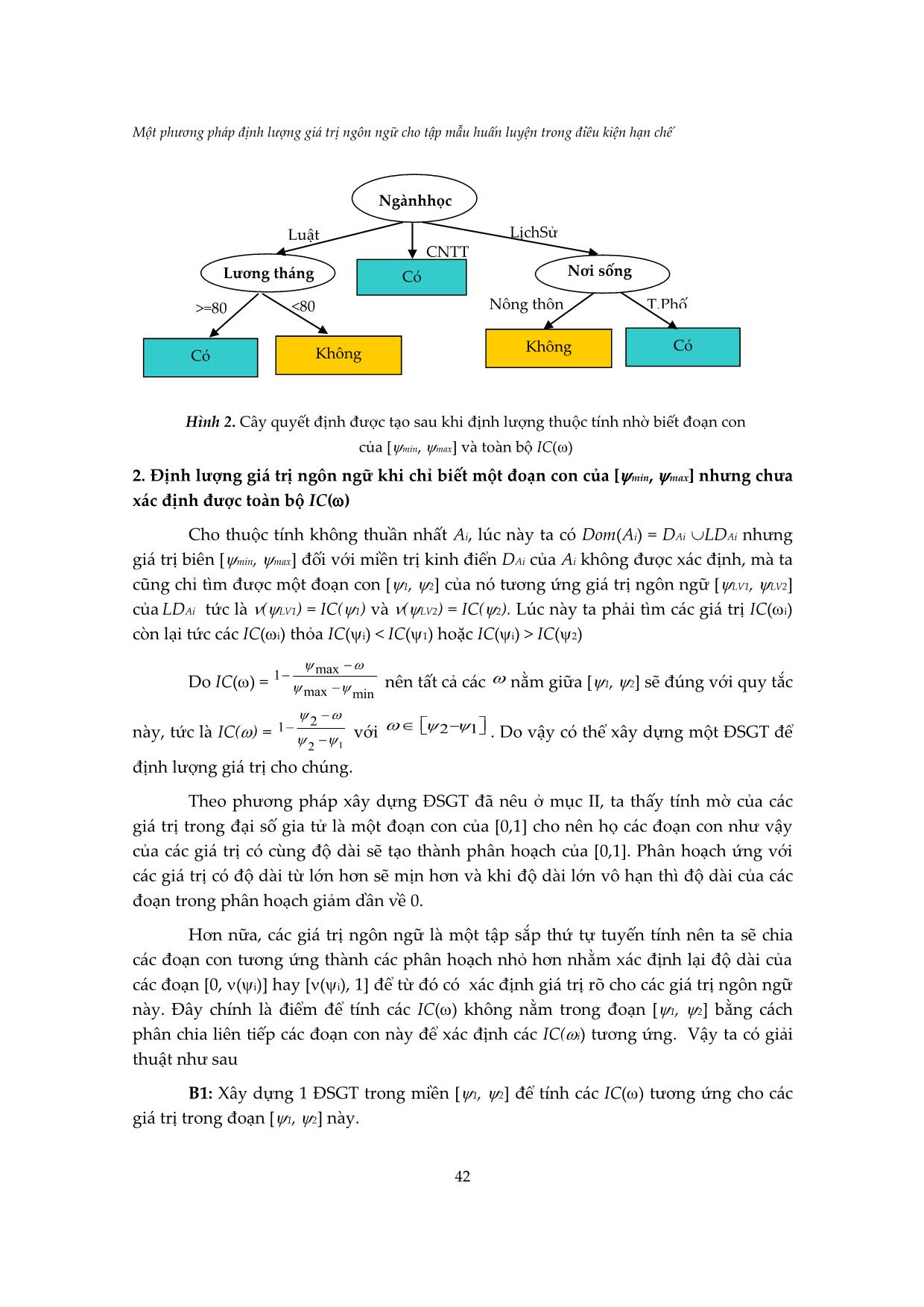
 Hình 3. Cây quyết định được tạo sau khi định lượng thuộc tính 
 khi chỉ biết đoạn con của [min, max] 
 B2: Tính cho các giá trị ngoài khoảng bằng cách tìm các phân hoạch thích hợp 
của các khoảng mờ để chèn các giá trị ngoại lai vào các khoảng này. Do giá trị Rất cao > 
Hơn cao nên ta sẽ phân hoạch đoạn *0.79,1+ tương ứng của |I(lớn)|. Như vậy ta có: 
 fm(Rất cao) ~ fm(Hơn cao) x I(Hơn cao) = 0.21 x 0.79 = 0.17. Nên I(Hơn cao) = [0.79, 
0.96], I(Rất cao) = *0.96, 1+. Do đó Rất cao = 97. Rất thấp < Hơn thấp nên ta sẽ phân hoạch 
đoạn *0, 0.14+ tương ứng của |I(thấp)|. fm(Rất thấp) ~ fm(Hơn thấp) x I(Hơn thấp) = 0.14 x 
0.14 = 0.02. Nên I(Hơn thấp) = [0.02, 0.14], I(Rất thấp) = *0, 0.02+. Do đó Rất thấp = 4. 
 44 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 14, Số 1 (2019) 
 B3: Tính lại IC() với *1, 2] = [4, 97]. Lúc này ta có: IC() = {0.47, 0.24, 0.52, 0, 
0.64, 0.81, 1, 0.27, 0.81, 0.49, 1, 0.40, 0.54, 0.49}. 
 Vậy thuộc tính LươngTháng sau khi được định lượng có giá trị là: {48, 26, 52, 4, 
64, 79, 97, 29, 79, 50, 97, 41, 54, 50}. Cây quyết định sau khi huấn luyện như hình 3. 
VI. KẾT LUẬN 
 Bài báo đã đánh giá tính phức tạp của dữ liệu huấn luyện được chọn từ dữ liệu 
nghiệp vụ, phân tích tính đa dạng của miền trị thuộc tính đồng thời chỉ ra tính phức 
tạp khi định lượng giá trị ngôn ngữ. Trên cơ sở của đại số gia tử, bằng việc xem xét 
tính hiệu quả khi làm thuần nhất giá trị cho các thuộc tính chưa thuần nhất trong mẫu 
theo giá trị ngôn ngữ hay theo giá trị kinh điển, bài báo đã chỉ ra một cách thức để có 
thể xác định được giá trị rõ cho các giá trị ngôn ngữ trong điều kiện hạn chế, để từ đó 
ta có thể huấn luyện được cây quyết định phù hợp với thực tế. 
 TÀI LIỆU THAM KHẢO 
[1]. Nguyễn Cát Hồ. Lý thuyết tập mờ và Công nghệ tính toán mềm, Tuyển tập các bài giảng 
 về Trường thu hệ mờ và ứng dụng (2006). 
[2]. Nguyễn Cát Hồ. Cơ sở dữ liệu mờ với ngữ nghĩa đại số gia tử, Bài giảng trường Thu - Hệ 
 mờ và ứng dụng, Viện Toán học Việt Nam (2008). 
[3]. Nguyễn Công Hào, Nguyễn Cát Hồ, Một cách tiếp cận xấp xỉ dữ liệu trong cơ sở dữ liệu 
 mờ, Tạp chí Tin học và Điều khiển học (2006). 
[4]. Lê Văn Tường Lân. Một cách tiếp cận chọn tập mẫu huấn luyện cây quyết định dựa trên 
 đại số gia tử, Hội nghị Quốc gia lần thứ VI về nghiên cứu cơ bản và ứng dụng Công nghệ 
 Thông tin (FAIR), Nhà xuất bản Khoa học tự nhiên và Công nghệ (2013). 
[5]. A.K. Bikas, E. M. Voumvoulakis and N. D. Hatziargyriou. Neuro-Fuzzy Decision Trees for 
 Dynamic Security Control of Power Systems, Department of Electrical and Computer 
 Engineering, Greece (2008) 
[6]. Chida, A. Enhanced Encoding with Improved Fuzzy Decision Tree Testing Using CASP 
 Templates, Computational Intelligence Magazine, IEEE (2012). 
[7]. [Chang, Robin L. P. Pavlidis. Fuzzy Decision Tree Algorithms, Man and Cybernetics, IEEE 
 (2007). 
[8]. Dorian, P.. Data Preparation for Data Mining, Morgan Kaufmann (1999). 
[9]. Daveedu R. A., Jaya Suma. G, Lavanya Devi. G. Construction of Fuzzy Decision Tree using 
 Expectation Maximization Algorithm, International Journal of Computer Science and 
 Management Research (2012). 
[10]. Fernandez A., Calderon M., Barrenechea E.. Enhancing Fuzzy Rule Based Systems in 
 Multi-Classication Using Pairwise Coupling with Preference Relations, EUROFUSE 
 45 
Một phương pháp định lượng giá trị ngôn ngữ cho tập mẫu huấn luyện trong điều kiện hạn chế 
 Workshop Preference Modelling and Decision Analysis, Public University of Navarra, 
 Pamplona, Spain (2009). 
[11]. FA. Chao Li, Juan sun, Xi-Zhao Wang. Analysis on the fuzzy filter in fuzzy decision trees, 
 Proceedings of the Second International Conference on Machine Learxung and Cybernetics 
 (2003). 
[12]. Kavita Sachdeva, Madasu Hanmandlu, Amioy Kumar. Real Life Applications of Fuzzy 
 Decision Tree, International Journal of Computer Applications (2012). 
[13]. Hesham A. Hefny, Ahmed S. Ghiduk, Ashraf Abdel Wahab. Effective Method for 
 Extracting Rules from Fuzzy Decision Trees based on Ambiguity and Classifiability, 
 Universal Journal of Computer Science and Engineering Technology, Cairo University, 
 Egypt. (2010). 
[14]. Ho Tu Bao. Introduction to knowledge discovery and data mining, Institute of Information 
 Technology National Center for Natural Science (2000). 
[15]. Ho N. C. and Nam H. V.. An algebraic approach to linguistic hedges in Zadeh's fuzzy 
 logic, Fuzzy Sets and Systems, vol.129, pp.229-254 (2002). 
[16]. Moustakidis, S. Mallinis, G. ; Koutsias, N. ; Theocharis, J.B. ; Petridis, V. . SVM-Based 
 Fuzzy Decision Trees for Classification of High Spatial Resolution Remote Sensing Images, 
 Geoscience and Remote Sensing, IEEE (2012). 
[17]. Oleksandr Dorokhov, Vladimir Chernov. Application of the fuzzy decision trees for the 
 tasks of alternative choices, Transport and Telecommunication Institute, Lomonosova, 
 Latvia , Vol.12, No 2 (2011). 
 A METHOD TO DETERMINE THE LINGUISTIC VALUES IN THE LIMITED 
 CONDITIONS OF TRAINING DATA SET 
 Le Van Tuong Lan 
 Faculty of Information Technology, University of Sciences, Hue University 
 Email: lvtlan@yahoo.com 
 ABSTRACT 
 Sample training data set plays an important role in the training process. When the 
 value of the attribute domain may be value or linguistics, we need a method to 
 homogenise sample training data set. Hedge algebra is a useful tool to make the 
 training set homogeneous by changing the values of mixed domain to 
 homogeneous data domain that only contains linguistics or values. In the process 
 of homogeneous data domain, we have to know the values min, max. However, in 
 reality, we do not know the values min, max exactly. In this paper, we present a 
 46 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 14, Số 1 (2019) 
 method to determine the linguistic values when we only know the sub values [1, 
 2] without knowing the values [min, max] exactly. 
 Keywords: Fuzzy decision tree, linguistic values, training data set. 
 Lê Văn Tƣờng Lân sinh năm 1974 tại thành phố Huế. Ông tốt nghiệp cử 
 nhân chuyên ngành Toán – Tin học tại Trường Đại học Khoa học, Đại học 
 Huế năm 1996 và thạc sĩ chuyên ngành Công nghệ thông tin tại Trường 
 Đại học Bách khoa Hà Nội, năm 2002. Hiện đang là Nghiên cứu sinh tại 
 Trường Đại học Khoa học, Đại học Huế, chuyên ngành Khoa học máy 
 tính. Ông công tác tại khoa Công nghệ thông tin, Trường Đại học Khoa 
 học, Đại học Huế từ năm 1996 đến nay. 
 Lĩnh vực nghiên cứu: Khai phá dữ liệu, công nghệ phần mềm. 
 47 
Một phương pháp định lượng giá trị ngôn ngữ cho tập mẫu huấn luyện trong điều kiện hạn chế 
 48