Modeling of the Dalat Nuclear Research Reactor (DNRR) with the Serpent 2 Monte Carlo code

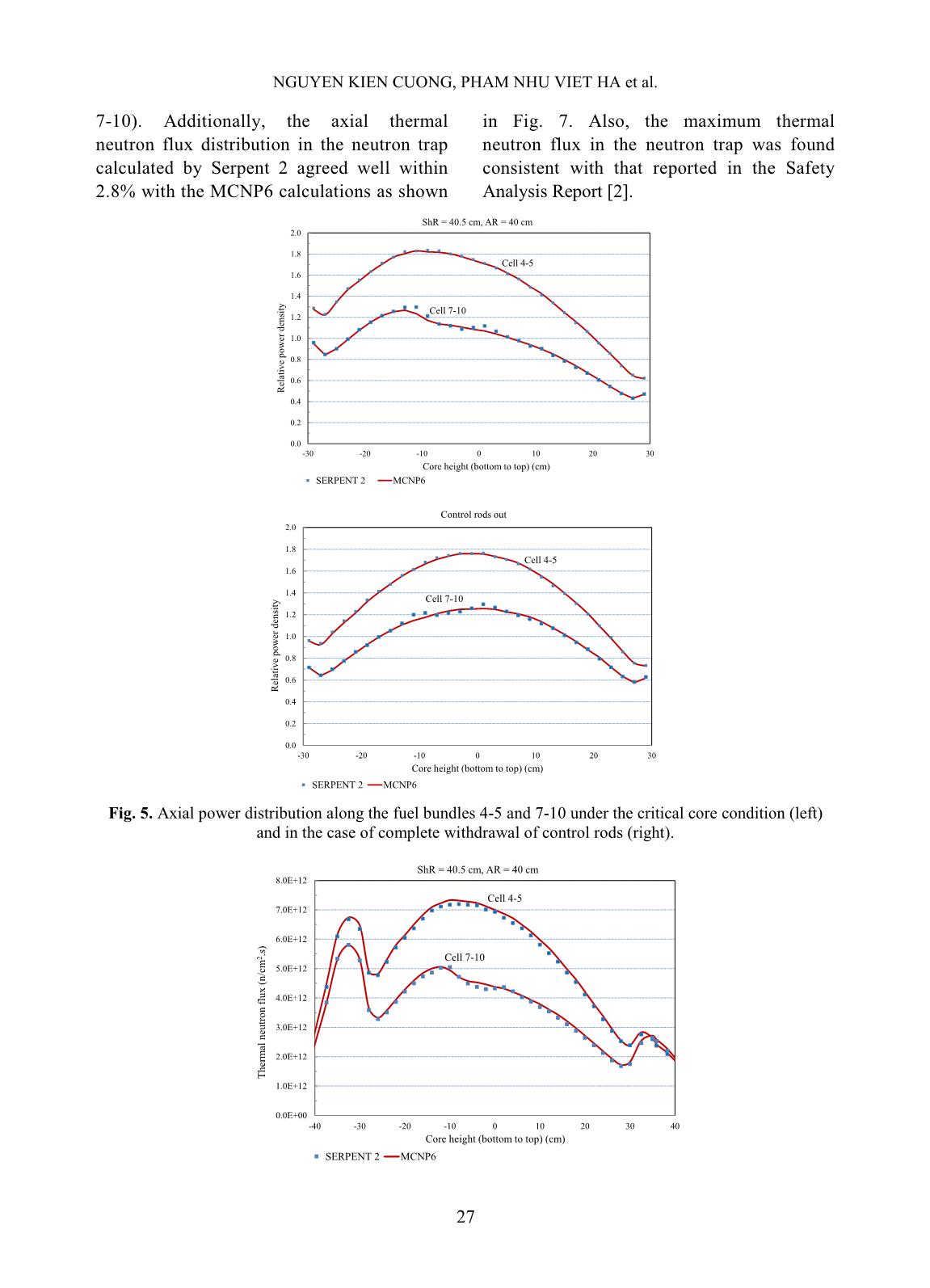
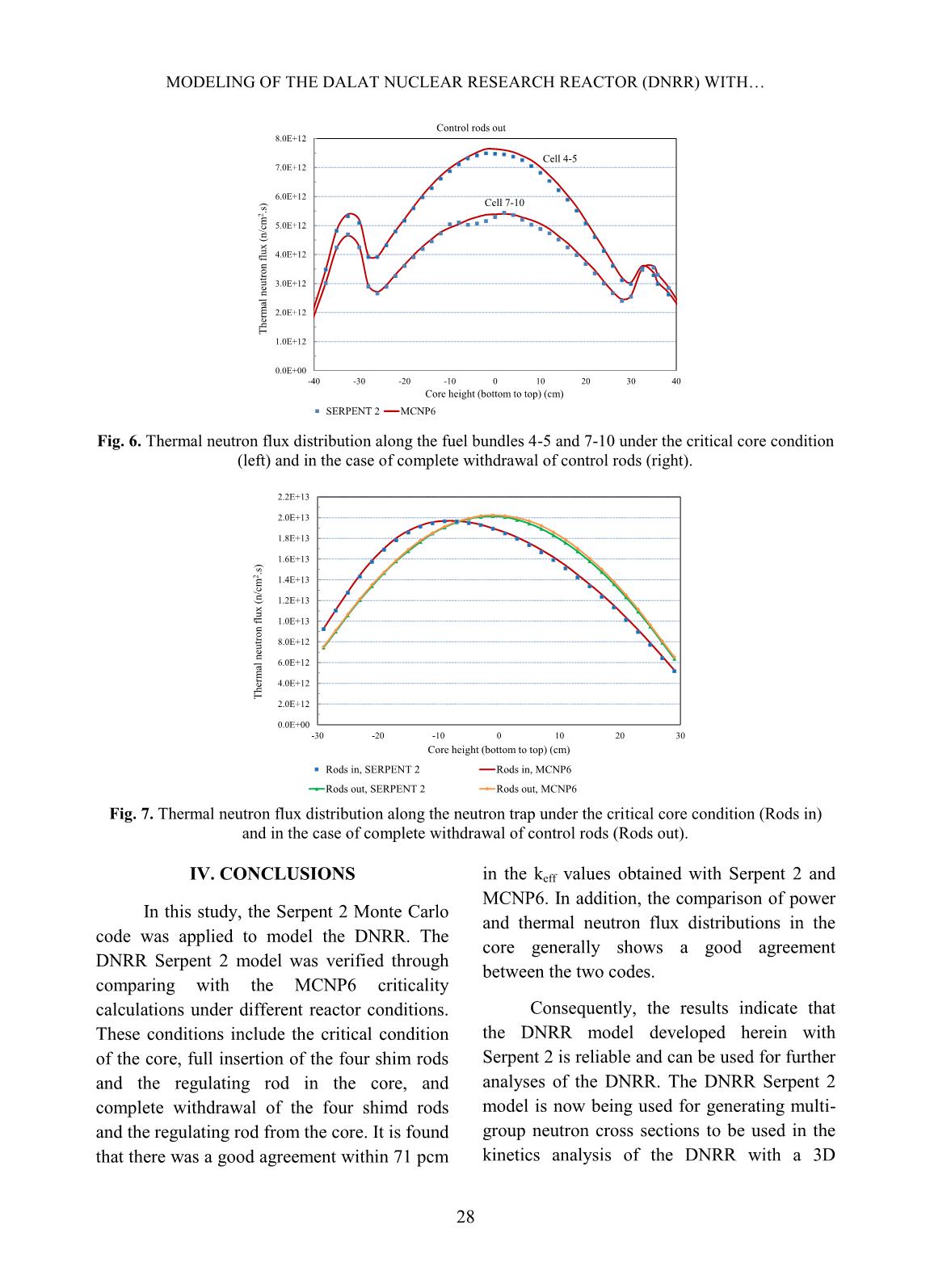
ks. The beryllium blocks 
have the same outer shape and dimension with 
the fuel bundle. At several peripheral cells, if 
no fuel bundle is loaded, the beryllium blocks 
are loaded for providing supplementary 
neutron reflection. A ring of serrated beryllium 
blocks is also located between the active core 
and the graphite reflector to act as an additional 
NGUYEN KIEN CUONG, PHAM NHU VIET HA et al. 
23 
reflector. This beryllium ring and the core are 
placed in a cylindrical aluminum shell, which 
is the lower section of the supporting structure. 
The thickness of the graphite reflector is 30.5 
cm. The core and the graphite reflector are 
placed in the reactor pool. 
In this work, the DNRR configuration 
with 92 LEU fuel bundles (Fig. 2) was simulated 
using the Serpent 2 Monte Carlo code [8]. The 
DNRR model with Serpent 2 was then verified 
through comparing with the MCNP6 criticality 
calculations under different reactor conditions 
including the critical condition and the cases of 
complete withdrawal and full insertion of the four 
shim rods and the regulating rod. The radial 
layout of the DNRR core modeled in MCNP6 
and Serpent 2 was shown in Fig. 3. The 
ENDF/B-VII.0 data library [9] was used in both 
the Serpent 2 and MCNP6 calculations. The 
parameters to be calculated and compared 
include the keff; radial power distributions; axial 
power distributions in cell 4-5 and cell 7-10; and 
axial thermal neutron flux distributions in cell 4-5, 
cell 7-10 and neutron trap. 
The DNRR model with MCNP6 was 
developed similarly to that reported with 
MCNP5 in Ref. [5]. It is noted that the 
DNRR model with MCNP had been well 
validated against experiments and other 
calculation results obtained with different 
codes [2][5]. By using MCNP, the complex 
geometry of the DNRR including the fuel 
bundles, control rods, in-core irradiation 
channels, beryllium rods, horizontal beam 
tubes, graphite reflector, rotary specimen 
rack, thermal column and thermalizing 
column was simulated with high accuracy 
and detail. This calculation model covers 
from the active core to reactor tank following 
the radial direction with 198.72 cm in 
diameter and the axial direction with 187 cm 
in height. Tallies 4 and 7 were used for 
calculating the neutron flux and power 
distributions, respectively. Then a DNRR 
model was developed with Serpent 2 using 
the same input data for the reactor geometry 
and materials with the MCNP6 model as 
described below. 
Fig. 1. Horizontal cross section view of the DNRR. 
MODELING OF THE DALAT NUCLEAR RESEARCH REACTOR (DNRR) WITH 
24 
Serpent is a three-dimensional 
continuous-energy Monte Carlo reactor 
physics burnup calculation code developed at 
the VTT Technical Research Centre of 
Finland [8]. Similar to MCNP, the code 
allows easily modeling of complicated reactor 
geometries for criticality calculations, fuel 
cycle studies, etc. Furthermore, it has also 
various powerful capabilities such as 
automated burnup sequence for spatial 
homogenization, coupled multi-physics 
calculations, transient simulations, sensitivity 
calculations, reactor geometry pre-
implementation and fast running time. 
Therefore, Serpent 2 has been widely used in 
the calculations of nuclear reactors in general 
and of TRIGA reactors in particular [10][11]. 
To simulate the DNRR geometry with high 
detail in the Serpent 2 model, we adopted all 
the data that were input to the DNRR MCNP6 
model as above mentioned. The only 
simplification is that the rounded corners of 
the outer hexagonal tubes of the VVR-M2 
fuel bundles were not modeled in the Serpent 
2 simulation. It is worth noting that the delta 
tracking method was used in the Serpent 2 
calculations as compared to the track length 
method used in the MCNP6 calculations. 
Fig. 2. Radial layout of the VVR-M2 fuel bundle (left) and configuration of the DNRR core with 92 LEU bundles 
(right). SR: safety rod, ShR: shim rod, and AR: automatic regulating rod. 
Fig. 3. The DNRR core with 92 LEU bundles modeled in MCNP6 (left) and Serpent 2 (right). 
NGUYEN KIEN CUONG, PHAM NHU VIET HA et al. 
25 
Table I. Main specifications of the DNRR. 
Reactor type Pool type 
Nominal thermal power 500 kW 
Coolant and moderator Light water 
Core cooling mechanism Natural convection 
Reflector Graphite, beryllium and light water 
Active core height 60 cm 
Core equivalent diameter 44.2 cm 
Fuel pitch 3.5 cm 
Fuel type 
VVR-M2 type, dispersed UO2-Al with 19.75% enrichment, 
aluminium cladding 
Number of control rods 7 (2 safety rods, 4 shim rods, 1 regulating rod) 
Material of safety and shim rods B4C 
Material of automatic regulating rod Stainless steel 
Vertical irradiation channels 4 (1 neutron trap, 1 wet channel, 2 dry channels) 
Horizontal beam ports 4 (1 tangential, 3 penetrant) 
III. RESULTS AND DISCUSSION 
A. Effective neutron multiplication factor 
The keff values obtained by Serpent 2 
and MCNP6 in the cases of (a) criticality 
condition (four shim rods were inserted 40.5 
cm in the core and the regulating rod was 
inserted 40 cm in the core), (b) complete 
withdrawal of the four shim rods and the 
regulating rod from the core, and (c) full 
insertion of the four shim rods and the 
regulating rod in the core were shown in Table 
II. In all the calculations, the two safety rods 
were assumed completely withdrawn from the 
core as they are used only for emergency 
shutdown. In this investigation, the four shim 
rods were inserted in the core and then the 
position of the regulating rod was adjusted 
correspondingly to search for the criticality of 
the core. It can be seen that there was a good 
agreement within 71 pcm in the keff values 
calculated using Serpent 2 and MCNP6. Also, 
the statistic errors of the keff values in the 
Serpent 2 and MCNP6 calculations were 
almost identical to each other with the same 
number of neutron history used. The difference 
in the keff values of at most 71 pcm might be 
mainly related to the two reasons as follows: 
(1) the rounded corners of the outer hexagonal 
tubes of the VVR-M2 fuel bundles were not 
included in the Serpent 2 model, and (2) 
different neutron tracking methods used in the 
Serpent 2 (delta tracking method) and MCNP6 
(track length method) calculations. 
Table II. Comparison of keff calculated using Serpent 2 and MCNP6. 
Position of control rods (cm) keff 
Four shim rods Regulating rod Serpent 2 MCNP6 Deviation 
(pcm) 
MODELING OF THE DALAT NUCLEAR RESEARCH REACTOR (DNRR) WITH 
26 
Full insertion Full insertion 0.97103 0.00007 0.97140 0.00006 -37 
Complete withdrawal Complete withdrawal 1.07864 0.00007 1.07793 0.00005 71 
40.5 40 1.00073 0.00007 1.00018 0.00006 55 
B. Power and thermal neutron flux 
distributions 
In this Section, power and thermal 
neutron flux distributions were calculated 
and analyzed using Serpent 2 in comparison 
with the MCNP6 calculations. The two 
cases including the criticality of the core 
and complete withdrawal of the shim rods 
and the regulating rod as shown in Table II 
were considered. Fig. 4 displays the relative 
radial power distributions calculated by 
Serpent 2 and MCNP6. It can be seen that 
there was a good agreement between the 
two codes. The maximum difference in the 
radial power distributions calculated by 
Serpent 2 and MCNP6 in the cases was 6.2% 
(critical condition) and -5.7% (complete 
withdrawal of control rods), which appeared 
at the fuel bundles located in the periphery 
of the core. The maximum value of the 
relative radial power distribution was found 
at cell 4-5 in both cases. This value was 
1.424 under the critical condition and 1.374 
in case of complete withdrawal of control 
rods. Hence, the insertion of control rods 
under the critical condition increased the 
maximum value of the radial power 
distribution 3.6%. 
Fig. 4. Relative radial power distribution in the core under the critical condition (left) and in the case of 
complete withdrawal of control rods (right). The upper and lower values were obtained with Serpent 2 and 
MCNP6, respectively. 
The axial power and thermal neutron 
flux distributions in cell 4-5 and cell 7-10 were 
shown in Figs. 5-6. Cell 4-5 is the position at 
which the relative radial power was highest 
and cell 7-10 is the position next to the 
regulating rod, which can show clearly the 
effect of control rod insertion. Fig. 5 shows a 
good agreement between the axial power 
distributions obtained with Serpent 2 and 
MCNP6 in these two cells. The respective 
maximum difference between the codes was 
1.5% (cell 4-5) and 4.9% (cell 7-10). Similarly, 
the axial thermal neutron flux distributions in 
cell 4-5 and cell 7-10 calculated by Serpent 2 
compared well with those calculated by 
MCNP6 as shown in Fig. 6. The respective 
maximum difference between the codes in 
this case was 3.3% (cell 4-5) and -4.2% (cell 
NGUYEN KIEN CUONG, PHAM NHU VIET HA et al. 
27 
7-10). Additionally, the axial thermal 
neutron flux distribution in the neutron trap 
calculated by Serpent 2 agreed well within 
2.8% with the MCNP6 calculations as shown 
in Fig. 7. Also, the maximum thermal 
neutron flux in the neutron trap was found 
consistent with that reported in the Safety 
Analysis Report [2]. 
Fig. 5. Axial power distribution along the fuel bundles 4-5 and 7-10 under the critical core condition (left) 
and in the case of complete withdrawal of control rods (right). 
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
-30 -20 -10 0 10 20 30
R
el
at
iv
e 
p
o
w
er
 d
en
si
ty
Core height (bottom to top) (cm)
ShR = 40.5 cm, AR = 40 cm
SERPENT 2 MCNP6
Cell 4-5
Cell 7-10
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
-30 -20 -10 0 10 20 30
R
el
at
iv
e 
p
o
w
er
 d
en
si
ty
Core height (bottom to top) (cm)
Control rods out
SERPENT 2 MCNP6
Cell 7-10
Cell 4-5
0.0E+00
1.0E+12
2.0E+12
3.0E+12
4.0E+12
5.0E+12
6.0E+12
7.0E+12
8.0E+12
-40 -30 -20 -10 0 10 20 30 40
T
h
er
m
al
 n
eu
tr
o
n
 f
lu
x
 (
n
/c
m
2
.s
)
Core height (bottom to top) (cm)
ShR = 40.5 cm, AR = 40 cm
SERPENT 2 MCNP6
Cell 4-5
Cell 7-10
MODELING OF THE DALAT NUCLEAR RESEARCH REACTOR (DNRR) WITH 
28 
Fig. 6. Thermal neutron flux distribution along the fuel bundles 4-5 and 7-10 under the critical core condition 
(left) and in the case of complete withdrawal of control rods (right). 
Fig. 7. Thermal neutron flux distribution along the neutron trap under the critical core condition (Rods in) 
and in the case of complete withdrawal of control rods (Rods out). 
IV. CONCLUSIONS 
In this study, the Serpent 2 Monte Carlo 
code was applied to model the DNRR. The 
DNRR Serpent 2 model was verified through 
comparing with the MCNP6 criticality 
calculations under different reactor conditions. 
These conditions include the critical condition 
of the core, full insertion of the four shim rods 
and the regulating rod in the core, and 
complete withdrawal of the four shimd rods 
and the regulating rod from the core. It is found 
that there was a good agreement within 71 pcm 
in the keff values obtained with Serpent 2 and 
MCNP6. In addition, the comparison of power 
and thermal neutron flux distributions in the 
core generally shows a good agreement 
between the two codes. 
Consequently, the results indicate that 
the DNRR model developed herein with 
Serpent 2 is reliable and can be used for further 
analyses of the DNRR. The DNRR Serpent 2 
model is now being used for generating multi-
group neutron cross sections to be used in the 
kinetics analysis of the DNRR with a 3D 
0.0E+00
1.0E+12
2.0E+12
3.0E+12
4.0E+12
5.0E+12
6.0E+12
7.0E+12
8.0E+12
-40 -30 -20 -10 0 10 20 30 40
T
h
er
m
al
 n
eu
tr
o
n
 f
lu
x
 (
n
/c
m
2
.s
)
Core height (bottom to top) (cm)
Control rods out
SERPENT 2 MCNP6
Cell 4-5
Cell 7-10
0.0E+00
2.0E+12
4.0E+12
6.0E+12
8.0E+12
1.0E+13
1.2E+13
1.4E+13
1.6E+13
1.8E+13
2.0E+13
2.2E+13
-30 -20 -10 0 10 20 30
T
h
er
m
al
 n
eu
tr
o
n
 f
lu
x
 (
n
/c
m
2
.s
)
Core height (bottom to top) (cm)
Rods in, SERPENT 2 Rods in, MCNP6
Rods out, SERPENT 2 Rods out, MCNP6
NGUYEN KIEN CUONG, PHAM NHU VIET HA et al. 
29 
reactor kinetics code. Also, this model with 
Serpent 2 is being planned for performing fuel 
burnup calculations of the DNRR. 
ACKNOWLEDGMENTS 
This research is funded by Ministry of 
Science and Technology of Vietnam under 
grant number DTCB.06/18/VKHKTHN. The 
visit of Pham Nhu Viet Ha in North Carolina 
State University during this work was 
supported by the IAEA TC Project VIE9016. 
REFERENCE 
[1]. TRIGA History, URL: 
 (accessed on 
April 4, 2017. 
[2]. Safety Analysis Report (SAR) for the Dalat 
Nuclear Research Reactor, Nuclear Research 
Institute, Dalat, Vietnam, 2012. 
[3]. N. N. Dien, L. B. Vien, L. V. Vinh, D. V. 
Dong, N. X. Hai, P. N. Son, and C. D. Vu, 
“Results of operation and utilization of the 
Dalat nuclear research reactor,” Nuclear 
Science and Technology, 4(1), 1-9, 2014. 
[4]. Q. B. Do, P. L. Nguyen, “Application of a 
genetic algorithm to the fuel reload 
optimization for a research reactor,” Applied 
Mathematics and Computation 187, 977, 2007. 
[5]. G. Phan, H. N. Tran, K. C. Nguyen, V. P. 
Tran, V. K. Hoang, P. N. V. Ha, and H. A. T. 
Kiet, “Comparative analysis of the Dalat 
nuclear research reactor with HEU fuel using 
SRAC and MCNP5,” Science and Technology 
of Nuclear Installations, Article ID 2615409, 
Volume 2017. 
[6]. Q. B. Do, G. T. T. Phan, K. C. Nguyen, Q. H. 
Ngo, H. N. Tran, “Criticality and rod worth 
analysis of the DNRR research reactor using 
the SRAC and MCNP5 codes,” Nuclear 
Engineering and Design 343, 197-209, 2019. 
[7]. D. B. Pelowitz et al., MCNP6TM User’s 
Manual, Version 1.0, LA-CP-13-00634, Rev. 
0, 2013. 
[8]. J. Leppänen, M. Pusa, T. Viitanen, V. 
Valtavirta, and T. Kaltiaisenaho. “The Serpent 
Monte Carlo code: Status, development and 
applications in 2013,” Annals of Nuclear 
Energy 82, 142-150, 2015. 
[9]. M. B. Chadwick, P. Obloˇzinsk´y, M. Herman 
et al., ENDF/B-VII.0: next generation 
evaluated nuclear data library for nuclear 
science and technology, Nucl. Data Sheets, 
Special Issue on Evaluated Nuclear Data File 
ENDF/B-VII.0, 2006. 
[10]. D. Ćalić, G. Žerovnik, A. Trkov, L. Snoj, 
“Validation of the Serpent 2 code on TRIGA 
Mark II benchmark experiments,” Applied 
Radiation and Isotopes 107, 165-170, 2016. 
[11]. C. Castagna, D. Chiesa, A. Cammi, S. Boarin, 
E. Previtali, M. Sisti, M. Nastasi, A. Salvini, 
G. Magrotti, M. Prata, “A new model with 
Serpent for the first criticality benchmarks of 
the TRIGA Mark II reactor,” Annals of 
Nuclear Energy 113, 171-176, 2018.