Mô hình hàng đợi retrial trong mạng WLAN với cơ chế kênh bảo vệ phân đoạn FGC

n trạng thái được chỉ ra trong Hình
3), do đó X có thể biểu diễn thông qua các ma trận Aj, Bj, Cj (đều có kích thước
(c + 1) × (c + 1)) như sau [11-14]:
 • Aj(i, k): ma trận chuyển trạng thái từ (i, j) đến (k, j) (với ,0 ≤ i, k ≤ c, j ≥ 0)
 do việc yêu cầu một cuộc gọi thành công (bao gồm cả các cuộc gọi chuyển vùng
 và cuộc gọi mới) hoặc một cuộc gọi rời khỏi hệ thống do đã được phục vụ. Aj
 có các phần tử khác không Aj(i, i − 1) = iµ, i = 1, c và Aj(i, i + 1) = λi =
 βiλF + λH , i = 0, c − 1. Lưu ý do j là mức độc lập nên ta có Aj = A.
 0 λ0 0 ... 0 0 0 
 0 0 λ1 ... 0 0 0 
 . . . . . 
 Aj = A = . . . .. .  , (j ≥ 0)
  
 0 0 0 ... (c − 1)µ 0 λc−1
 0 0 0 ... 0 cµ 0
 • Bj (i, k): ma trận chuyển trạng thái từ (i, j) đến (k, j + 1) (với 0 ≤ i, k ≤ c,
 j ≥ 0) do một cuộc gọi mới đi vào bị từ chối và chuyển vùng sang mạng WLAN
 hoặc một cuộc gọi chuyển vùng đi vào nhưng khi đó tất cả các kênh đều bận
 phục vụ và chuyển vùng sang mạng WLAN. Bj có các phần tử khác không là
 Bj (i, i) = (1 − βi) PimλF , i = 0, c − 1 và Bj (c, c) = Pimλ. Tương tự như trên,
 ta cũng có Bj = B.
38
 Tạp chí Khoa học và Kỹ thuật - Học viện KTQS - Số 190 (04-2018)
 Hình 3. Mô hình trạng thái
 (1 − β0)PimλF ... 0 0 
  0 ... 0 0 
  . . . . 
 Bj = B =  . .. . .  , (j ≥ 0)
  
  0 ... (1 − β1−βc−1 )PimλF 0 
 0 ... 0 Pimλ
 • Cj (i, k): ma trận chuyển trạng thái từ (i, j) đến (k, j − 1) (với 0 ≤ i, k ≤ c, j ≥ 1)
 do một cuộc gọi chuyển vùng mạng WLAN quay lại và được phục vụ hoặc rời
 khỏi hệ thống mãi mãi nhưng chưa được phục vụ. Cj có các phần tử khác không
 là Cj (i, i + 1) = jαH , i = 0, c − 1 và Cj (c, c) = (1 − P im) jαH .
  
 0 jαH 0 ··· 0 0
 0 0 jαH ··· 0 0 
 . . . . . . 
 Cj = C = . . . . . .  , (j ≥ 1)
  
 0 0 0 ··· 0 jαH 
 0 0 0 ··· 0 (1 − P im) jαH
Khi đó ta có ma trận sinh Q tổng quát như sau:
 39
Chuyên san Công nghệ thông tin và Truyền thông - Số 11 (04-2018)
  (0) (0) 
 Q1 Q2
 Q(1) Q(1) Q(1) 
  0 1 2 
  (2) (2) (2) 
 Q =  Q0 Q1 Q2 
  (3) (3) . 
  Q Q ..
  0 1 
 ... ...
 (j) (j) A Cj (j)
 Với Q2 = B, Q1 = A − D − B − D (j ≥ 0),Q0 = Cj(j ≥ 1). Do hệ thống
của ta là vô hạn nên ta có thể xấp xỉ các giá trị j ≥ N theo [15], như sau:
 
 jαH , j < N
 αH (j) =
 M (N) αH , j ≥ N
 Với M(N) = E(J|J ≥ N) là kỳ vọng số cuộc gọi trong mạng WLAN và không
nhỏ hơn N . Khi đó ta có thể xấp xỉ C = Cj (với j ≥ N):
  
 0 M (N) αH 0 ··· 0 0
 0 0 M (N) αH ··· 0 0 
 . . . . . . 
 Cj = C = . . . . . .  , (j ≥ N)
  
 0 0 0 ··· 0 M (N) αH 
 0 0 0 ··· 0 (1 − P im) M (N) αH
 (j) A C (j)
Dễ dàng suy ra Q1 = Q1 = A − D − B − D (j ≥ 0),Q0 = C(j ≥ N). Do đó theo
 j−N+1
phương pháp nhân ma trận ta có vj = vN−1R , (j ≥ N − 1) với R là nghiệm tối
thiểu không âm thỏa:
 2
 B + RQ1 + R C = (0, 0,..., 0)
 | {z }
 c+1
Domenech-Benlloch [15] đã đề xuất 2 giải thuật gọi là HM2 và Simple Substitution để
ước lượng giá trị M(N) thỏa mãn độ hội tụ M cho trước dựa vào hệ thức sau đây:
 P∞  −1 
 −1
 j=N jvje vN R(I − R) + NI (I − R) e
 M (N) = P∞ = −1 (1)
 j=N vje vN (I − R) e
.
 Giải thuật HM2:
 Trong đó vN được tính từ N phương trình cân bằng đầu:
 (j−1) (j) (j+1)
 vj−1Q2 + vjQ1 + vj+1Q0 = (0, 0,..., 0)
 | {z }
 c+1
40
 Tạp chí Khoa học và Kỹ thuật - Học viện KTQS - Số 190 (04-2018)
 Algorithm 1: HM2
 Đầu vào :
 • Các ma trận A, B, Cj;
 • Giá trị N;
 • Độ chính xác mong muốn: M ;
 Đầu ra :
 • Giá trị M(N) thoả mãn độ hội tụ M ;
1 Gán M0(N) = N;
2 Gán k = 1;
  |Mk(N)−Mk−1(N)| 
3 while < M do
 Mk−1(N)
4 Tính ma trận R theo giải thuật Simple Substitution;
 −1 −1
 vN (R(I−R) +NI)(I−R) e
5 Mk (N) = −1 ;
 vN (I−R) e
6 k = k + 1;
Với j = 0,N − 1 và v−1 = 0.
 Sau khi tìm được giá trị M(N) ta tính được v0, v1,. . . , vN−1 và từ phương trình
 PN−2 −1
chuẩn hoá: j=0 vje + vN−1(I − R) e = 1 ta tính được vj (j ≥ N).
2.5. Các thông số hiệu năng của hệ thống
 • Xác suất tắc nghẽn của các cuộc gọi mới PBF : hệ thống từ chối các cuộc gọi
 mới đến (với xác suất 1 − βi theo cơ chế FGC).
 PN−2 −1
 PBF = j=0 vj (e − β) + vN−1(I − R) (e − β) (2)
 T
 Với β = (β0, β1, . . . , βc−1, 0) .
 • Xác suất tắc nghẽn của các cuộc gọi chuyển vùng PBH : xảy ra khi có một yêu
 cầu chuyển vùng đến được tiếp nhận theo cơ chế FGC nhưng khi đó tất cả kênh
 của hệ thống đều bận.
 PN−2 −1
 PBH = j=0 vjz + vN−1(I − R) z (3)
 Với z = (0, 0,..., 0, 1)T .
 | {z }
 c+1
3. Phân tích kết quả
 Ta mô hình hệ thống với các tham số như sau (nếu không đề cập đến cơ chế FGC
thì ta mặc định sử dụng cơ chế LFGC). Các kết quả phân tích được mô tả về mặt đồ
thị (viết bằng ngôn ngữ Matlab) sự biến thiên của xác suất tắc nghẽn phụ thuộc vào
lưu lượng tải mạng (ρ). Các tham số mô phỏng được lựa chọn dựa theo các nghiên cứu
trong [11-12] và được mô tả ở Bảng 1.
 41
Chuyên san Công nghệ thông tin và Truyền thông - Số 11 (04-2018)
 Algorithm 2: Simple Substitution
 Đầu vào :
 • Các ma trận B, Q1,C;
 • Độ chính xác mong muốn: R;
 Đầu ra :
 • Ma Trận R với độ chính xác mong muốn;
1 Gán R = 0;
2 Gán k = 0;
 −1
3 Gán V = −BQ1 ;
 −1
4 Gán W = −CQ1 ;
5 while k Rk − Rk−1 k≥ R do
 2
6 Rk = −V − R(k−1)W ;
7 k = k + 1;
 Tên thông số Ký hiệu Giá trị
 Số lượng kênh trong mạng cellular c 9
 Số kênh cho phép g 8
 Xác suất cho phép một cuộc gọi mới nhận dịch vụ p 0.5
 Tải lưu lượng ρ = λ/ (cµ) 0.4
 Tốc độ đến của cuộc gọi chuyển vùng λH 6/425
 Tốc độ đến của cuộc gọi mới λF 12/425
 Tốc độ phục vụ mạng cellular µ 1/85
 Tốc độ retrial chuyển từ mạng WLAN sang mạng αH 1/6
 cellular
 Xác suất kiên nhẫn của khách hàng Pim 0.6
3.1. Phân tích và so sánh xác suất tắc nghẽn theo giá trị ρ
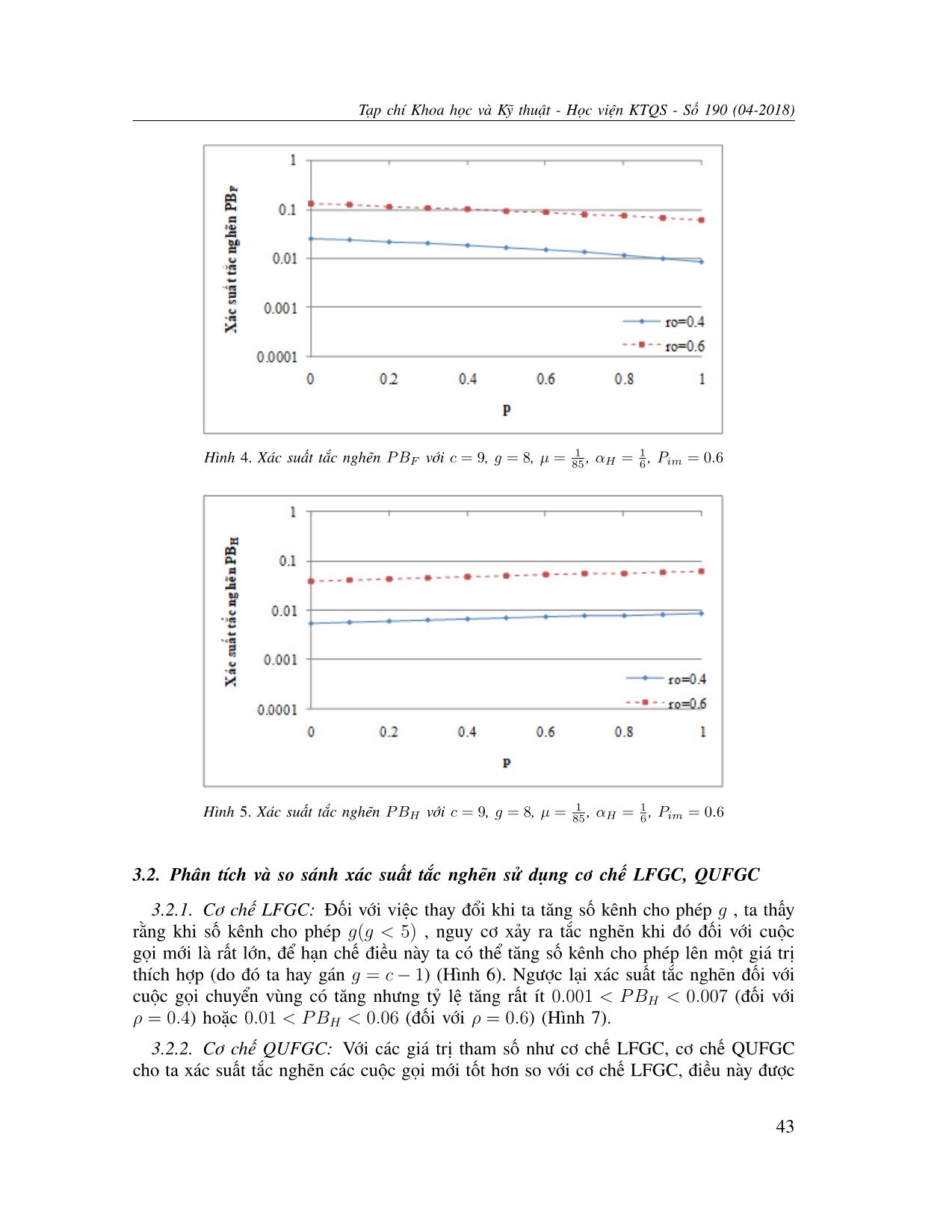
 Từ kết quả phân tích ta thấy rằng xác suất tắc nghẽn PBF giảm dần khi ta tăng giá
trị xác suất cho phép p (Hình 4) là do khả năng cho phép các cuộc gọi mới đi vào
càng cao thì hiển nhiên xác suất tắc nghẽn PBF sẽ càng thấp, trong khi đó xác suất
tắc nghẽn PBH tăng ít khi ta tăng giá trị p (Hình 5). Ngoài ra ta còn thấy với giá trị
ρ1 = 0.4 đều cho ta xác suất tắc nghẽn PBF và PBH tốt hơn giá trị ρ2 = 0.6 hay
λ2 > λ1 (tương ứng với giá trị ρ1 và ρ2) do tốc độ đến cuộc các gọi lớn hơn thì khả
năng tắc nghẽn càng cao. Điều này hoàn toàn phù hợp với các công thức (2) và (3) và
định nghĩa tải lưu lượng chứng tỏ tính đúng đắn của mô hình.
42
 Tạp chí Khoa học và Kỹ thuật - Học viện KTQS - Số 190 (04-2018)
 1 1
 Hình 4. Xác suất tắc nghẽn PBF với c = 9, g = 8, µ = 85 , αH = 6 , Pim = 0.6
 1 1
 Hình 5. Xác suất tắc nghẽn PBH với c = 9, g = 8, µ = 85 , αH = 6 , Pim = 0.6
3.2. Phân tích và so sánh xác suất tắc nghẽn sử dụng cơ chế LFGC, QUFGC
 3.2.1. Cơ chế LFGC: Đối với việc thay đổi khi ta tăng số kênh cho phép g , ta thấy
rằng khi số kênh cho phép g(g < 5) , nguy cơ xảy ra tắc nghẽn khi đó đối với cuộc
gọi mới là rất lớn, để hạn chế điều này ta có thể tăng số kênh cho phép lên một giá trị
thích hợp (do đó ta hay gán g = c − 1) (Hình 6). Ngược lại xác suất tắc nghẽn đối với
cuộc gọi chuyển vùng có tăng nhưng tỷ lệ tăng rất ít 0.001 < P BH < 0.007 (đối với
ρ = 0.4) hoặc 0.01 < P BH < 0.06 (đối với ρ = 0.6) (Hình 7).
 3.2.2. Cơ chế QUFGC: Với các giá trị tham số như cơ chế LFGC, cơ chế QUFGC
cho ta xác suất tắc nghẽn các cuộc gọi mới tốt hơn so với cơ chế LFGC, điều này được
 43
Chuyên san Công nghệ thông tin và Truyền thông - Số 11 (04-2018)
 1 1
 Hình 6. Xác suất tắc nghẽn PBF với c = 9, p = 0.5, µ = 85 , αH = 6 , Pim = 0.6
 1 1
 Hình 7. Xác suất tắc nghẽn PBH với c = 9, p = 0.5, µ = 85 , αH = 6 , Pim = 0.6
giải thích là do khi có cùng số kênh cho phép g như nhau, khi đó đối với c − g kênh
còn lại QUFGC cho phép các cuộc gọi mới đi vào với xác suất p, khác với LFGC chỉ
cho duy nhất một kênh còn lại trong c − g kênh được phục vụ với xác suất p (Hình 8).
Trong khi đó, nếu so với cơ chế LFGC thì xác suất tắc nghẽn cuộc gọi chuyển vùng
theo cơ chế QUFGC lại cho ta giá trị cao hơn nhưng không nhiều (Hình 9).
3.3. Phân tích và so sánh xác suất tắc nghẽn đối với giá trị λF /λH
 Từ Hình 10 ta thấy rằng với giá trị ρ cố định (hay giá trị λ = λF + λH là cố định)
thì khi tỷ lệ λF /λH thay đổi xác suất tắc nghẽn lại ít thay đổi. Điều này nói lên rằng
44
 Tạp chí Khoa học và Kỹ thuật - Học viện KTQS - Số 190 (04-2018)
 1 1
 Hình 8. Xác suất tắc nghẽn PBF với c = 9, p = 0.5, µ = 85 , αH = 6 , Pim = 0.6
 1 1
 Hình 9. Xác suất tắc nghẽn PBH với c = 9, p = 0.5, µ = 85 , αH = 6 , Pim = 0.6
xác suất tắc nghẽn PBF và PBH ít phụ thuộc vào tỷ lệ λF /λH (hay λF /λ ) mà chỉ
phụ thuộc vào tổng tốc độ đến (λ = λF + λH ).
3.4. Phân tích và so sánh xác suất tắc nghẽn theo giá trị ρ
 Ta thấy rằng khi tải lưu lượng ρ(ρ < 0.6) thấp thì giá trị xác suất tắc nghẽn (cả cuộc
gọi mới và cuộc gọi chuyển vùng) là rất nhỏ và khi giá trị ρ ≥ 1 thì xác suất tắc nghẽn
khi đó sẽ xảy ra rất lớn. Điều này nói lên rằng tốc độ đến λ càng cao (hay ρ càng cao
do tỷ lệ thuận) thì hiển nhiên khả năng tắc nghẽn của hệ thống là rất lớn (Hình 11).
 Như vậy, với các kết quả phân tích ở trên, mô hình mà bài báo đưa ra đáp ứng các
yêu cầu trong việc phân tích để đảm bảo xác suất tắc nghẽn của các cuộc gọi chuyển
 45
Chuyên san Công nghệ thông tin và Truyền thông - Số 11 (04-2018)
 1 1
 Hình 10. Xác suất tắc nghẽn với c = 15, ρ = 0.4, µ = 85 , αH = 6 , Pim = 0.6
 1 1
 Hình 11. Xác suất tắc nghẽn với c = 15, g = 8, µ = 85 , αH = 6 , Pim = 0.6
vùng luôn thấp hơn các cuộc gọi mới dựa vào số kênh cho phép cuộc gọi mới đi vào g
và xác suất cho phép phục vụ đối với các cuộc gọi mới p. Các kết quả phân tích đảm
bảo độ tin cậy và chính xác, tuy nhiên, để kết quả có thể sát với thực tế hơn, mô hình
cần có được sự so sánh và đánh giá thông qua mô phỏng.
4. Kết luận
 Trong bài báo này, chúng tôi đã đề xuất một mô hình hàng đợi retrial dạng M/M/c
có xét đến tính kiên nhẫn của khách hàng để giải quyết bài toán chuyển vùng trong
mạng 3G-WLAN có sử dụng kênh bảo vệ phân đoạn FGC. Từ các kết quả phân tích đã
46
 Tạp chí Khoa học và Kỹ thuật - Học viện KTQS - Số 190 (04-2018)
chỉ ra rằng mô hình mà ta xây dựng là phù hợp và chính xác. Ngoài ra, trong mô hình
chúng tôi xây dựng đã có sự đánh giá, phân tích và so sánh giữa hai cơ chế FGC là
LFGC và QUFGC để giảm xác suất tắc nghẽn cuộc gọi mới nhưng vẫn phải đảm bảo
cuộc gọi chuyển vùng được bảo vệ theo cơ chế điều khiển tiếp nhận cuộc gọi CAC.
Tài liệu tham khảo
[1] N. Akar and K. Sohraby, “Finite and Infinite QBD Chains: A Simple and Unifying Algorithmic Approach”,
 Proceedings of IEEE INFOCOM, pp. 1105–1113, 1997.
[2] J.R. Artalejo, “Accessible bibliography on retrial queues”, Mathematical and Computer Modelling, pp. 1-6, no.
 30, 1999.
[3] F.A. Cruz-Pérez and L. Ortigoza-Guerrero, "Fractional Resource Reservation in Mobile cellular Systems",
 Resource, Mobility, and Security Management in Wireless Networks and Mobile Communications, pp. 335-362,
 2006.
[4] J.R. Artalejo, “A classi?ed bibliography of research on retrial queues: Progress in 2000-2009”. Mathematical
 and Computer Modelling, pp. 1071-1081, vol. 51, 2010.
[5] J.R. Artalejo and G.I. Falin, “Standard and retrial queueing systems: A comparative analysis”. Revista Matemática
 Complutense, pp. 101-129, vol. 15, no. 1, 2002.
[6] J.R. Artalejo and A. Gómez-Corral, Retrial Queueing Systems: A Computational Approach, Springer, Berlin,
 2008.
[7] D. Bini and B. Meini, “On the Solution of a Nonlinear Matrix Equation Arising in Queueing Problems”, SIAM
 Journal on Matrix Analysis and Applications, pp. 906–926, vol. 17 , no. 4, 1996.
[8] D. Bini and B. Meini, “Improved Cyclic Reduction for Solving Queueing Problems”, Numerical Algorithms, pp.
 57–74, vol. 15, no. 1, 1997.
[9] D. Bini et al, “Structured Markov chains solver: algorithms”,In Proceedings of SMCtools 2006, ACM Press,
 Pisa, 2006
[10] M. Ghaderi and R. Boutaba, "Call Admission Control in Mobile Cellular Networks: a comprehensive survey",
 Wireless Communications and Mobile Computing, pp. 69-93, vol. 6, no. 1, 2006.
[11] T.V. Do, “Solution for A Retrial Queueing Problem in Cellular Networks with the Fractional Guard Channel
 Policy”, Mathematical and Computer Modelling, pp. 2058–2065, vol. 53, no. 11, (2011).
[12] T. V. Do, “A new computational algorithm for retrial queues to cellular mobile systems with guard channels”,
 Computers and Industrial Engineering, pp. 865–872, vol. 59, no. 4, 2010.
[13] T.V. Do, “An efficient method to compute the rate matrix for retrial queues with large number of servers”,
 Applied Mathematical Modelling, pp. 638-643, vol. 23, no. 5, 2010.
[14] T.V. Do, “An enhanced algorithm to solve multiserver retrial queueing systems with impatient customer”,
 Computers and Industrial Engineering, pp. 719-728, vol. 65, no. 4, 2013.
[15] M.J. Domenech-Benlloch et al, “Generalized Truncated Methods for an Efficient Solution of retrial Systems”,
 Mathematical Problems in Engineering, pp. 1-15., 2008.
[16] M.J. Domenech-Benlloch, “Efficient Method to Approximately Solve retrial Systems with Impatience”, Journal
 of Applied Mathematics, pp. 1-18, 2012.
[17] G.I. Falin, “A survey of retrial queues”, Queueing Systems, pp. 127-167, vol. 7, no. 2, 1990.
[18] G.I. Falin and J.G. Templeton, Retrial Queues, Chapman and Hall, New Jersey, 1997.
[19] R.M. Feldman and C. Valdez-Flores, Applied Probability and Stochastic Processes. Springer-Verlag Berlin
 Heidelberg, 2010.
[20] J.F. Gross et al, Fundamentals of Queueing Theory, John Wiley and Sons, New Jersey, 2008.
[21] J.L. Vazquez-Ávila and F.A. Cruz-Pérez, “Performance Analysis of Fractional Guard Channel Policies in Mobile
 Cellular Networks”, IEEE Transactions on Wireless Communications, pp. 301-305, vol. 5, no. 2, 2006.
[22] J.L. Vázquez-Ávila, F.A. Cruz-Pérez, and L. Ortigoza-Guerrero, “Performance comparison of fractional guard
 channel policies in mobile cellular networks”, Proc. IEEE PIMRC04, pp. 1476–1480, 2004.
[23] T.V. Do , N.H. Do, Á. Horváth, J. Wang, “Modelling opportunistic spectrum renting in mobile cellular
 networks”, Journal of Network and Computer Applications, pp. 129-138, vol. 52, 2016.
 Ngày nhận bài 29-11-2017; Ngày chấp nhận đăng 21-03-2018.
 
 47
Chuyên san Công nghệ thông tin và Truyền thông - Số 11 (04-2018)
 Đặng Thanh Chương sinh năm 1975 tại Thành phố Vinh; Tốt nghiệp Đại học ngành Vật lý
 tại Đại học Khoa học Huế năm 1997; Nhận bằng Thạc sĩ chuyên ngành Tin học năm 2004
 tại Đại học Khoa học Huế, bằng Tiến sĩ tại Viện Công nghệ thông tin, Viện Hàn lâm khoa
 học và công nghệ Việt Nam năm 2014; Hiện công tác tại Khoa Công nghệ thông tin, Đại học
 Khoa học, Đại học Huế. Hướng nghiên cứu: Mạng OBS, Đánh giá hiệu năng mạng.
 Hoa Lý Cương Sinh năm 1990 tại An Giang. Tốt nghiệp ĐH Công nghệ thông tin chuyên
 ngành Kỹ thuật phần mềm tại trường ĐH Khoa học Tự nhiên, ĐH Quốc gia thành phố Hồ Chí
 Minh, năm 2012. Nhận bằng Thạc sĩ chuyên ngành Khoa học Máy tính, Trường ĐH Khoa
 học, ĐH Huế, năm 2017.
 Email: hlcuong90@gmail.com
48