Kỹ thuật phân lớp để giải mã hiệu quả mã LDPC trong hệ thống thông tin di động 5G

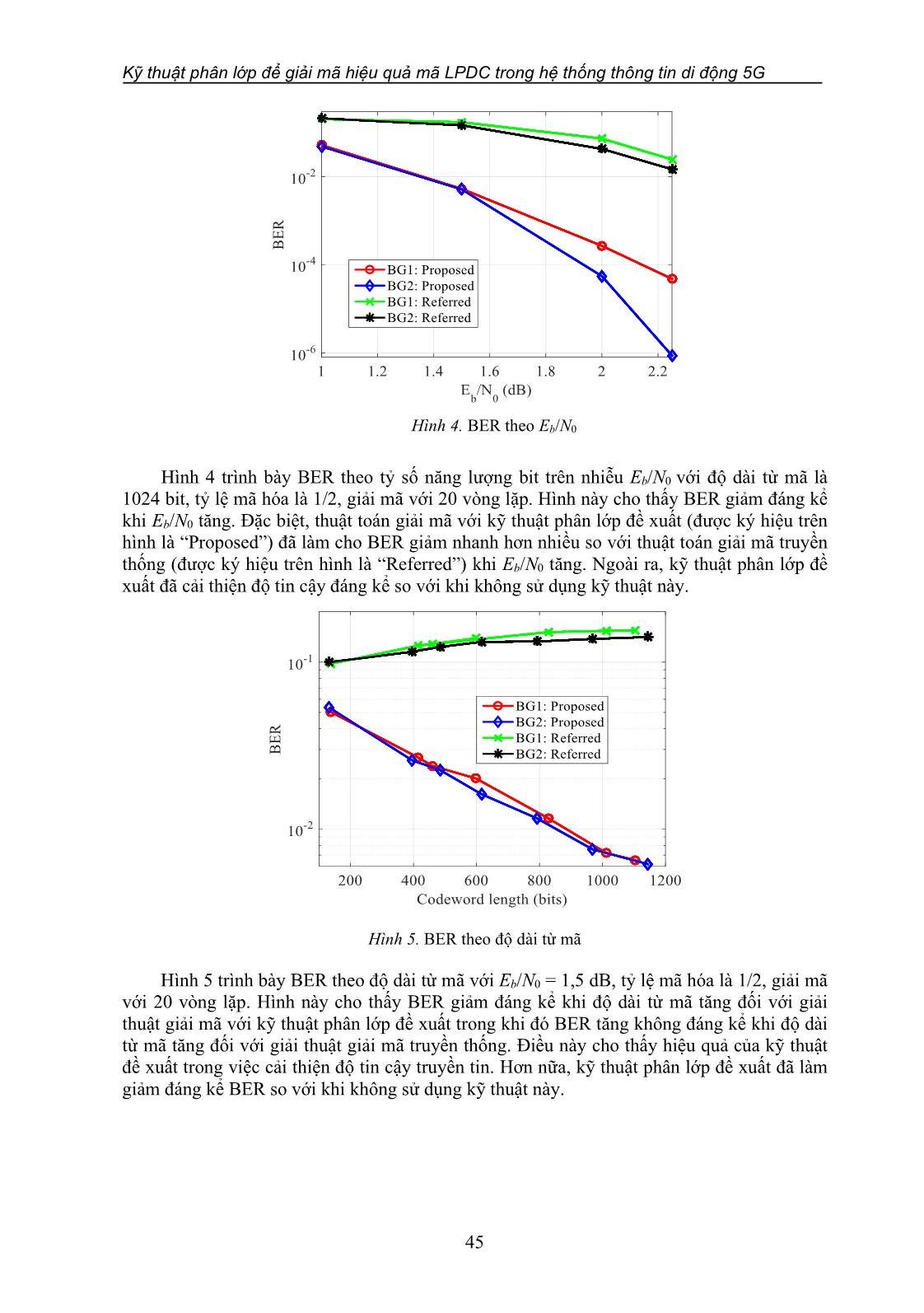
n tất cả các giá trị 
 asi, j j . Trong phép toán modulo 2, λi có được bằng cách thực hiện các phép toán XOR trên 
tất cả các phần tử của asi, j j . Các giá trị λi có thể được ước tính trên mỗi chu kỳ xung nhịp 
trong g = 4 chu kỳ. Khối thứ nhất của các bit chẵn lẻ p được tính bằng cách tích lũy tất cả 
 a1
các giá trị λi. Các cặp bit chẵn lẻ còn lại có thể được lấy bằng một phương pháp có thể dễ 
dàng suy ra từ phương trình (19)-(21). Quá trình này có thể được thực hiện trong 2 chu kỳ 
xung nhịp vì có sự phụ thuộc giữa p và p . Tất cả các bit chẵn lẻ pa trong phần chẵn lẻ 
 a3 a4
đầu tiên được lưu trữ trong các thanh ghi dịch. 
 Trong bước thứ hai, phần pc có thể được xác định dễ dàng dựa trên phương trình (10), 
trong đó ma trận C1 và C2 được cho bởi 
 c1,1 c 2,1 c 1,k c 1, k+ 1 c 2, k + 2 c 1, k + g 
 b b b b 
 c c c c c c
 CC== 2,1 2,2 2,kb 2,1 k b+ 2,2 k b + 2, k b + g (22) 
 12 
 c c c c c c 
 mgb−,1 mg b − ,2 mgk b − , b mgk b − , b + 1 mgk b − , b + 2 mgkg b − , b + 
 Khi áp dụng phương trình (10), các phần tử của pc có thể được tính bằng các phương 
trình sau: 
 41 
Nguyễn Trọng Duy, Hồ Văn Khương 
 kb g
 p=+ c s c p ,
 c1 1, j j 1, kbj+ j a
 jj==11
 kb g
 p=+ c s c p ,
 c2 2, j j 2, kbj+ j a (23) 
 jj==11
 kb g
 pc=+ c m− g,, j s j c m − g k + j p a .
 mb − g b b b j
 jj==11
 Tương tự, csi, j j biểu thị sự chuyển dịch vòng của sj với hệ số dịch chuyển được xác 
định bởi ci,j và cp biểu thị sự chuyển dịch vòng của p với hệ số dịch chuyển được 
 i, kbj+ j a a j
xác định bởi c . Ngay sau khi thu được cs và cp, chúng có thể được sử dụng 
 i, kb + j i, j j i, kbj+ j a
để xác định giá trị của các bit chẵn lẻ tương ứng trong phần chẵn lẻ thứ hai pc. Bước này có 
thể được thực hiện trong một chu kỳ xung nhịp duy nhất. Do đó, tất cả các bit chẵn lẻ pc có 
thể được thu thập trong chu kỳ xung nhịp (mb-g). Sau đó, từ mã là sự kết hợp của thông điệp 
ban đầu s và hai phần chẵn lẻ được tính toán pa và pc. 
3.2. Giải mã 
 Sum-product là tên chung cho một lớp thuật toán giải mã Maximum Likelihood (ML) [13]. 
Thuật toán sử dụng thông tin kênh truyền và các giá trị từ kênh truyền. Thuật toán tạo ra một 
giá trị xác suất cho mỗi bit nhận được và làm mới giá trị này sau nhiều lần lặp để tìm ước 
lượng cho bit đó. 
 Mã LDPC (N, K) là mã nhị phân được đặc trưng bởi ma trận kiểm tra chẵn lẻ thưa HM×N 
trong đó M = N - K có thể được biểu diễn bằng đồ hình Tanner của các nút biến 
nN 1, ,  và các nút kiểm tra mM 1, ,  . Biểu thị tập hợp các nút biến được kết 
nối với một nút kiểm tra m nào đó là  m. Một nút biến n được kết nối với nút kiểm tra m 
nếu nm   . Ngoài ra, tập  mn\ biểu thị tập các nút biến được kết nối với nút kiểm 
tra m không bao gồm n. Tương tự, tập các nút kiểm tra nối với một nút biến nào đó n được 
ký hiệu là  n. Một nút kiểm tra được kết nối với nút biến n nào đó nếu mn  . Tập 
hợp  nm\ biểu thị tập hợp các nút kiểm tra được kết nối với nút biến n loại trừ m. 
 Thuật toán sum-product xử lý lặp đi lặp lại các bit nhận được theo các bước nối liền 
nhau có thể được nhìn thấy trên đồ hình Tanner dưới dạng bước ngang tiếp theo là bước dọc 
để cải thiện độ tin cậy của mỗi bit được giải mã. Các thước đo độ tin cậy được tính toán của 
các bit ở cuối bất kỳ lần lặp giải mã nào được sử dụng làm đầu vào của lần lặp tiếp theo. 
Thuật toán giải mã lặp này tiếp tục cho đến khi thỏa mãn một tiêu chí dừng nào đó. 
 Để minh họa, hãy xét độ tin cậy của một bit đã giải mã được đo bằng xác suất posteriori 
 , 1 nN. Sau đó, Log-Likelihood Ratio (LLR) của mỗi bit mã được tính bởi 
P( xn Y )
 P x= 0 Y
 ( n ) (24) 
 Lx( n ) = log 
 P( xn =1 Y )
 Trong mỗi lần lặp lại, một giá trị rmn→ được tính theo bước ngang tại mỗi nút kiểm tra 
m và được chuyển cho tất cả các nút biến n nếu nm   . Tương tự, mỗi nút biến n sẽ gửi 
 42 
Kỹ thuật phân lớp để giải mã hiệu quả mã LPDC trong hệ thống thông tin di động 5G 
một giá trị qnm→ trong bước dọc đến tất cả các nút kiểm tra m nếu mn  . 
 Từ mã được ký hiệu là X= x12,,, x xN  , trong đó xn 0,1. Các giá trị LLR của 
vector nhận được tương ứng được biểu thị bằng Y= y12,,, y yN . 
 Bước khởi tạo
 Bước ngang
 Bước dọc
 Bước quyết định
 Thỏa điều kiện 
 dừng vòng lặp? Không
 Có
 Các bit được giải mã
 Hình 2. Giải thuật giải mã sum-product 
 Quá trình giải mã sử dụng thuật toán sum-product có thể được thực hiện theo các bước 
liên tiếp như Hình 2. 
 Bước khởi tạo: Các giá trị ban đầu của LLR có thể nhận được từ đầu ra của bộ giải điều 
chế yn. Các giá trị ban đầu này được sử dụng làm qnm→ của lần lặp đầu tiên cho bước cập 
nhật nút kiểm tra (Bước ngang). 
 Bước ngang: Bước ngang tại nút kiểm tra m được dành riêng để xử lý các giá trị đến từ 
các nút biến qnm→ để tính toán các giá trị trả lời rmn→ cho mọi nm   . Vì vậy, đối với 
mỗi nút kiểm tra m: 
 q 
 rq= sgn( ) 2 tanh−1 tanh nm'→ (25) 
 m→→ n  n' m 
 n'\'\ ( m) n n ( m) n 2 
 Bước dọc: Bước dọc tại nút biến n được dành riêng để xử lý các giá trị đến từ các nút 
kiểm tra rmn→ để tính toán các giá trị trả lời qnm→ cho mọi mn  . Vì vậy, đối với mỗi 
nút biến n: 
 qn→→ m=+ y n r m' n( x n ) (26) 
 m'\ M( n) m
 Bước quyết định: Đối với mỗi nút biến, các giá trị LLR được cập nhật theo 
 L( xn) =+ y n r m→ n( x n ) (27) 
 mn ( )
 43 
Nguyễn Trọng Duy, Hồ Văn Khương 
 Các giá trị LLR được áp dụng cho quyết định cứng để quyết định về giá trị có thể có 
 T
của xn là 1 nếu Lx( n ) 0 và 0 nếu ngược lại. Syndrome Hxˆ sau đó được tính toán và 
kiểm tra để quyết định giải mã thành công nếu Syndrome bằng 0 hoặc tiến hành lặp lại tiếp 
theo nếu điều kiện Syndrome không được thỏa mãn. Quá trình này tiếp tục cho đến khi từ mã 
được giải mã thành công hoặc số lần lặp tối đa đã hết. 
3.3. Kỹ thuật phân lớp đề xuất 
 Để cải thiện hiệu năng giải mã của thuật toán sum-product, nhóm tác giả đề xuất kỹ 
thuật phân lớp. Kỹ thuật này tăng tính bảo mật cho quyết định của bit xn. Ưu điểm của kỹ 
thuật đề xuất là hệ số hiệu chỉnh làm giảm tổn thất hiệu năng và độ phức tạp của việc giải 
mã. Trong kỹ thuật này, chúng ta xem lớp đầu tiên là một tập hợp các nút biến có giá trị thấp 
của thông tin nội tại yn của bit xn. 
 Đối với mỗi lần lặp, chúng ta tính toán nút kiểm tra và nút biến trong một lớp. Việc giải 
mã sau đó diễn ra tuần tự. Điều này có nghĩa là ta sẽ tập hợp một số hàng của ma trận kiểm 
tra chẵn lẽ thành một lớp và thực hiện bước dọc trong giải thuật giải mã sum-product. Ma 
trận H sẽ được phân lớp thành như sau: 
 H1
 H
 H = 2 (28) 
 H NK−
trong đó mỗi khối hàng trong ma trận H là một lớp. 
 Hình 3 minh họa sơ đồ giải mã của kỹ thuật phân lớp đề xuất khi có 2 lớp trong đó: 
C1 là từ mã được mã hóa từ H1 và C2 là từ mã được mã hóa từ H2. Việc giải mã C1 sẽ sử 
dụng LLR trong vòng lặp đầu tiên, sau đó sẽ sử dụng LLR21 sau khi đã cập nhật cột. 
 LLR
 Giải mã cho C1
 LLR12 LLR21
 Giải mã cho C2
 Hình 3. Thuật toán giải mã đề xuất với kỹ thuật phân lớp 
 4. KẾT QUẢ MINH HỌA 
 Phần này trình bày các kết quả mô phỏng cho hệ thống truyền thông được điều chế 
BPSK (Binary Phase Shift Keying) với nhiễu Gaussian trắng cộng (Additive White Gaussian 
Noise - AWGN). Mã LDPC sử dụng 2 loại ma trận kiểm tra chẵn lẻ, BG1 và BG2, cho hệ 
thống thông tin di động 5G. Giải thuật mã hóa và giải mã đã được trình bày trong phần 3. 
 44 
Kỹ thuật phân lớp để giải mã hiệu quả mã LPDC trong hệ thống thông tin di động 5G 
 Hình 4. BER theo Eb/N0 
 Hình 4 trình bày BER theo tỷ số năng lượng bit trên nhiễu Eb/N0 với độ dài từ mã là 
1024 bit, tỷ lệ mã hóa là 1/2, giải mã với 20 vòng lặp. Hình này cho thấy BER giảm đáng kể 
khi Eb/N0 tăng. Đặc biệt, thuật toán giải mã với kỹ thuật phân lớp đề xuất (được ký hiệu trên 
hình là “Proposed”) đã làm cho BER giảm nhanh hơn nhiều so với thuật toán giải mã truyền 
thống (được ký hiệu trên hình là “Referred”) khi Eb/N0 tăng. Ngoài ra, kỹ thuật phân lớp đề 
xuất đã cải thiện độ tin cậy đáng kể so với khi không sử dụng kỹ thuật này. 
 Hình 5. BER theo độ dài từ mã 
 Hình 5 trình bày BER theo độ dài từ mã với Eb/N0 = 1,5 dB, tỷ lệ mã hóa là 1/2, giải mã 
với 20 vòng lặp. Hình này cho thấy BER giảm đáng kể khi độ dài từ mã tăng đối với giải 
thuật giải mã với kỹ thuật phân lớp đề xuất trong khi đó BER tăng không đáng kể khi độ dài 
từ mã tăng đối với giải thuật giải mã truyền thống. Điều này cho thấy hiệu quả của kỹ thuật 
đề xuất trong việc cải thiện độ tin cậy truyền tin. Hơn nữa, kỹ thuật phân lớp đề xuất đã làm 
giảm đáng kể BER so với khi không sử dụng kỹ thuật này. 
 45 
Nguyễn Trọng Duy, Hồ Văn Khương 
 Hình 6. BER theo tỷ lệ mã hóa 
 Hình 6 trình bày BER theo tỷ lệ mã hóa với Eb/N0 = 1,5 dB và giải mã với 20 vòng lặp. 
Hình này cho thấy BER giảm đáng kể khi tỷ lệ mã hóa tăng đối với giải thuật giải mã với kỹ 
thuật phân lớp đề xuất trong khi đó BER giảm không đáng kể khi tỷ lệ mã hóa tăng đối với 
giải thuật giải mã truyền thống. Tuy nhiên, đối với mọi giá trị của tỷ lệ mã hóa thì kỹ thuật 
phân lớp đề xuất đều đạt BER nhỏ hơn đáng kể so với khi không sử dụng kỹ thuật này. Điều 
này cho thấy hiệu quả của kỹ thuật đề xuất trong việc cải thiện độ tin cậy truyền tin. 
 Sử dụng công cụ đo thời gian thực của Matlab, chúng tôi đã khảo sát thời gian giải mã 
của thuật toán giải mã với Eb/N0 = 1 dB, giải mã với 20 vòng lặp, ma trận kiểm tra chẵn lẻ 
BG2 với Z = 52, 100 khối bit truyền. Kết quả đo được khi không sử dụng và sử dụng kỹ 
thuật phân lớp được trình bày lần lượt trên các Hình 7 và 8. Các hình này cho thấy thời gian 
giải mã giảm đáng kể từ khoảng 45,383 giây xuống còn 27,811 giây khi sử dụng kỹ thuật 
phân lớp. 
 Hình 7. Thời gian giải mã khi không sử dụng kỹ thuật phân lớp. “Function Name” = “Tên 
 hàm” dùng để tính thời gian thực hiện. Trong hình này thì tên hàm là BPSK_nrldpc_sim. 
 “Calls” là số hàm cần thực hiện để đo thời gian. “Total Time” là tổng thời gian thực hiện. 
 Hình 8. Thời gian giải mã khi sử dụng kỹ thuật phân lớp. “Function Name” = “Tên hàm” dùng 
 để tính thời gian thực hiện. Tên hàm là BPSK_nrldpc. “Calls” là số hàm cần thực hiện để đo 
 thời gian. “Total Time” là tổng thời gian thực hiện. 
 Tổng hợp các kết quả ở trên cho thấy, kỹ thuật phân lớp đã giảm đáng kể cả về tỷ lệ lỗi 
bit và thời gian giải mã. Điều này cho thấy ưu điểm của kỹ thuật phân lớp đề xuất. 
 46 
Kỹ thuật phân lớp để giải mã hiệu quả mã LPDC trong hệ thống thông tin di động 5G 
 5. KẾT LUẬN 
 Bài báo này đã đề xuất kỹ thuật phân lớp để giảm thời gian giải mã và tỷ lệ lỗi bit cho 
mã LDPC ứng dụng trong hệ thống thông tin di động 5G. Nhiều kết quả đã chứng minh các 
ưu điểm của kỹ thuật đề xuất bằng cách so sánh thuật toán giải mã sum-product khi sử dụng 
và khi không sử dụng kỹ thuật này theo nhiều thông số khác nhau như tỷ lệ năng lượng bit 
trên nhiễu, độ dài từ mã, tỷ lệ mã hóa. 
 Bài báo này đã hiện thực thuật toán mã hóa và giải mã cho mã LDPC ứng dụng trong 
hệ thống thông tin di động 5G sử dụng phần mềm Matlab. Hướng phát triển tiếp theo là đánh 
giá hiệu năng của mã LDPC trong điều kiện vận hành thực tế của hệ thống thông tin di động 
5G để đánh giá toàn diện khả năng triển khai của kỹ thuật phân lớp đề xuất. 
 TÀI LIỆU THAM KHẢO 
 1. Gallager R. - Low-density parity-check codes, IRE Transactions on Information 
 Theory 8 (1) (1962) 21-28. 
 2. MacKay D. J. C. and Neal R. M. - Near Shannon limit performance of low density 
 parity check codes, Electronics Letters 33 (6) (1997) 457-458. 
 3. Yuhai S., Chunjiang L. and Ming Y. - The application of LDPC code in ABS-S 
 system, in Proc. International Forum on Information Technology and Applications, 
 Chengdu, China (2009) 159-162. 
 4. Zhu K. and Wu Z. - Comprehensive study on CC-LDPC, BC-LDPC and polar code, 
 in Proc. IEEE Wireless Communications and Networking Conference Workshops 
 (WCNCW), Seoul, South Korea (2020) 1-6. 
 5. Sun Y., Karkooti M. and Cavallaro J. R. - High throughput, parallel, scalable LDPC 
 encoder/decoder architecture for OFDM systems, in Proc. IEEE Dallas/CAS 
 Workshop on Design, Applications, Integration and Software, Richardson, TX, USA 
 (2006) 39-42. 
 6. de Fez I., Fraile F., Belda R. and Guerri J. C. - Analysis and evaluation of adaptive 
 LDPC AL-FEC codes for content download services, IEEE Transactions on 
 Multimedia 14 (3) (2012) 641-650. 
 7. Wang Y., Ueng Y., Peng C. and Yang C. - A low-complexity LDPC decoder 
 architecture for WiMAX applications, in Proc. International Symposium on VLSI 
 Design, Automation and Test, Hsinchu, Taiwan (2011) 1-4. 
 8. Tsatsaragkos I. and Paliouras V. - A reconfigurable LDPC decoder optimized for 
 802.11n/ac applications, IEEE Transactions on Very Large Scale Integration (VLSI) 
 Systems 26 (1) (2018) 182-195. 
 9. Li H., Bai B., Mu X., Zhang J. and Xu H. - Algebra-assisted construction of quasi-
 cyclic LDPC codes for 5G new radio, IEEE Access 6 (2018) 50229-50244. 
 10. https://www.cohere-technologies.com/wp-content/uploads/2017/06/R1-1700859.pdf 
 11. Yasotharan H. and Carusone A. C. - A flexible hardware encoder for systematic 
 low-density parity-check codes, in Proc. IEEE International Midwest Symposium on 
 Circuits and Systems, Cancun, Mexico (2009) 54-57. 
 12. N. T. B. Tram, N. T. Tuy, and L. Hanho - Efficient QC-LDPC encoder for 5G new 
 radio, Electronics 8 (6) (2019) 1-15. 
 47 
Nguyễn Trọng Duy, Hồ Văn Khương 
 13. Emran A. A. and Elsabrouty M. - Simplified variable-scaled min sum LDPC decoder 
 for irregular LDPC codes, in Proc. IEEE Consumer Communications and 
 Networking Conference (CCNC), Las Vegas, NV, USA (2014) 518-523. 
 14. Liang T., Zhang P., Liu C. and Liu J. - Efficient encoding of quasi-cyclic low-density 
 parity-check codes, in Proc. IEEE Advanced Information Technology, Electronic and 
 Automation Control Conference (IAEAC), Chongqing, China (2018) 1189-1193. 
 15. Roberts M. K., Mohanram S. S., and Shanmugasundaram N. - An improved low 
 complex offset min-sum based decoding algorithm for LDPC codes, Mobile 
 Networks and Applications 24 (6) (2019) 1848-1852. 
 ABSTRACT 
 STRATIFYING TECHNIQUE FOR DECODING EFFICIENTLY LDPC CODES 
 IN 5G MOBILE COMMUNICATION SYSTEM 
 Nguyen Trong Duy, Ho Van Khuong* 
 Ho Chi Minh City University of Technology, VNU-HCM 
 *Email: hvkhuong@hcmut.edu.vn 
 The 5th Generation (5G) mobile communication system must meet three main criteria: 
wide bandwidth, high reliability and low latency. Low density parity check (LDPC) code 
was adopted for the 5G mobile communication system because the LDPC code reaches 
closely to the Shannon capacity. This paper proposes a stratifying technique to significantly 
reduce the decoding time and improve the bit error rate (BER). The performance of the 
proposed technique is evaluated in different system parameters such as energy-per-bit to 
noise power ratio, codeword length and code rate. 
Keywords: LDPC code, 5G, BER, sum-product, stratified decoding. 
 48