Improving performance of the asynchronous cooperative relay network with maximum ratio combining and transmit antenna selection technique

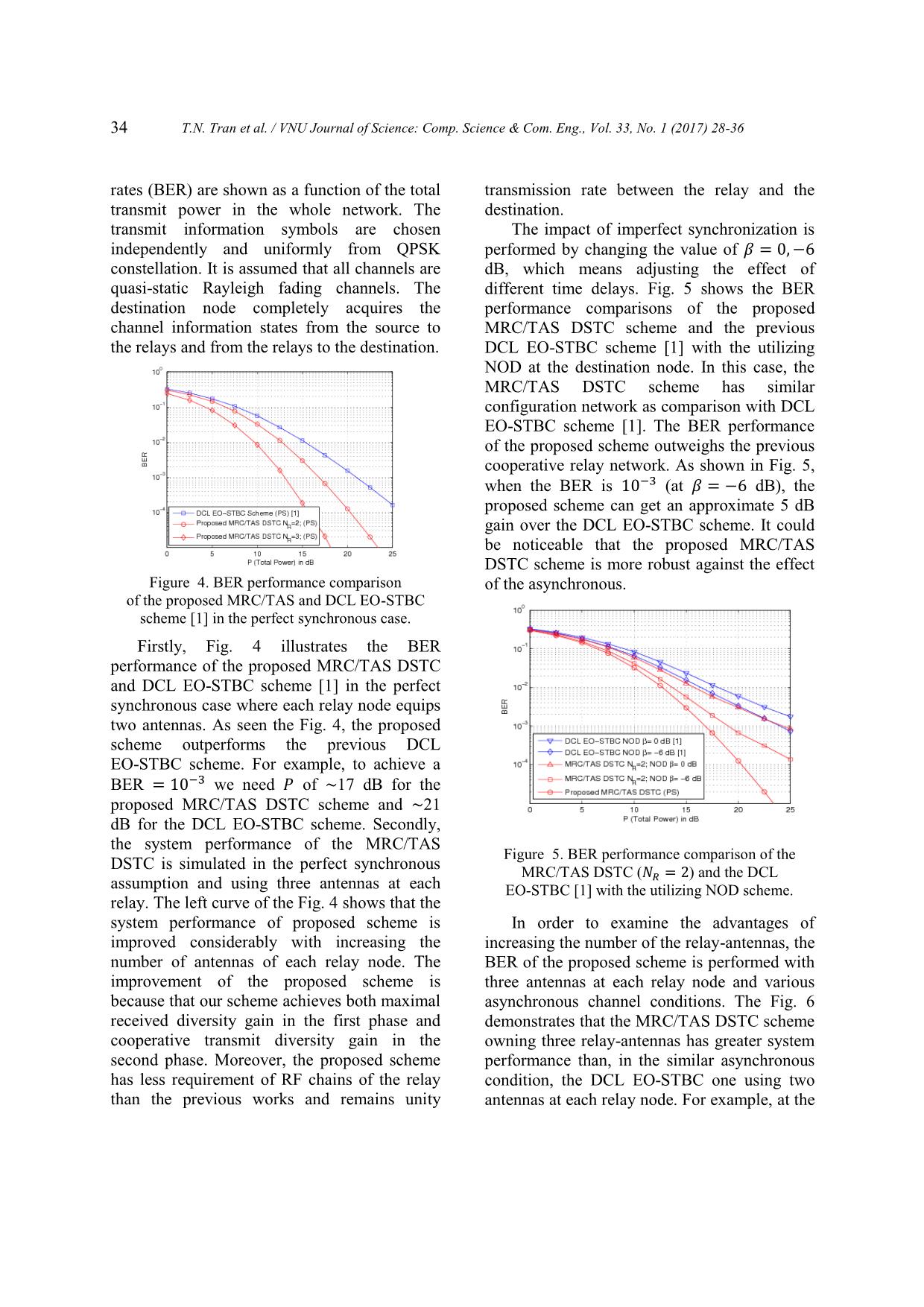
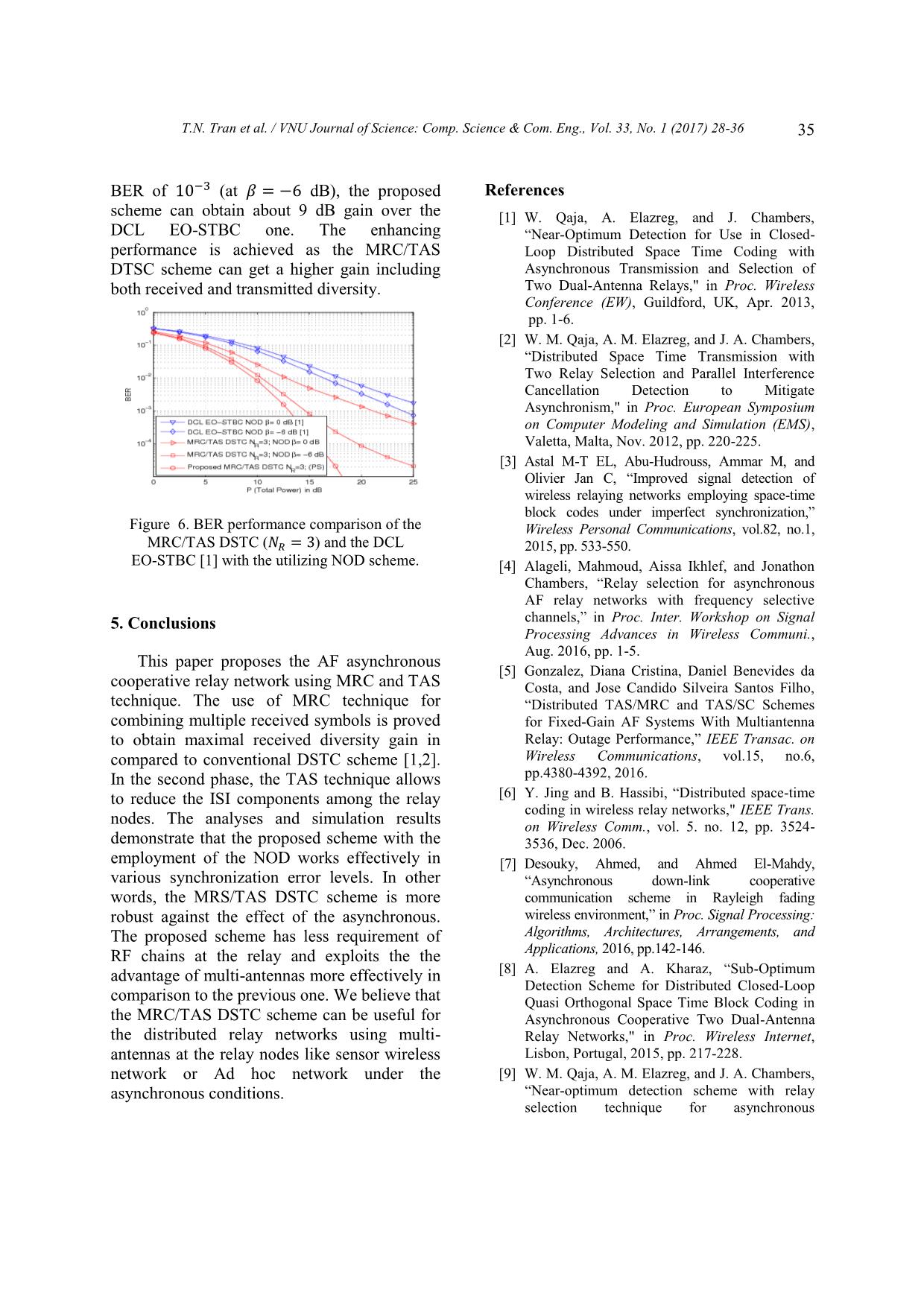
ntenna 퐭 (푛) is denotes the channel gain from the selected 
described by a linear function of 퐫 (푛) and its 
 ∗ transmit antenna of the 푡ℎ relay node to the 
conjugate 퐫 (푛) as follow destination node. The TAS technique allows to 
 푃2 ∗ achieve the transmitted diversity gain in the 
 퐭 (푛) = √ (퐀 퐫 (푛) + 퐁 퐫 (푛)).(4) 
 푃1+1 second phase. 
 G 
 Figure 3. Representation of ISI components between the selected transmit relay antenna 
 and the destination antenna. 
 As the previous mention in [1, 2], the whereas both antennas of the second relay node 
transmitted signals from the cooperative relay (denotes 푅2) and the destination node are 
nodes to the destination will undergo different synchronized imperfectly (푒. 𝑖. 휏2 = 휏12 =
time delays due to different locations of the 휏22 ≠ 0) as shown in Fig.3. The received 
relay nodes. Therefore, the received symbols at symbols at the destination are written as follow 
the destination node may not align. Without 
loss of generality, we assume that both antennas 퐲(1, 푛) = 퐭1(1, 푛) 1(푛) + 퐭2(1, 푛) 2(푛) 
of the first relay node (denotes 푅1) and the +퐭2(2, 푛 − 1) 2(푛 − 1) + 퐳(1, 푛), (6) 
destination node are synchronized perfectly, 
32 T.N. Tran et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 33, No. 1 (2017) 28-36 
 퐲(2, 푛) = 퐭1(2, 푛) 1(푛) + 퐭2(2, 푛) 2(푛) + 퐈i푛푡(1, 푛)
퐭2(1, 푛) 2(푛 − 1) + 퐳(2, 푛), (7) 퐈i푛푡(푛) = [ ]
 퐈i푛푡(2, 푛)
 ∗
 where 퐳(푛) is the additive Gaussian noise ‖ 2‖퐹 2(푛 − 1)퐬 (1, 푛 − 1)
 = [ ∗ ∗ ], 
vector at the destination. By substituting (4) ‖ 1‖퐹 2(푛 − 1)퐬 (2, 푛)
into (6) and (7), then taking the conjugate of and 
퐲(2, 푛), the received symbols at the destination 퐰(푛)
can be rewritten as ∗
 푃2 1(푛)퐯1(1, 푛) − 2(푛)퐯2(2, 푛)
 푃2푃1 = √ [ ∗ ∗ ∗ ] 
 퐲(1, 푛) = √ (‖ 1‖퐹 1(푛)퐬(1, 푛) + 1 + 푃1 1(푛)퐯1(2, 푛) + 2(푛)퐯2(1, 푛)
 1+푃1
‖ ‖ ) 퐳(1, 푛)
 2 퐹 2(푛)퐬(2, 푛) + [ ]. 
 퐳∗(2, 푛)
 푃 푃
 2 1 ∗ As similar literatures, the effects of ISIs 
 +√ ‖ 2‖퐹 2(푛 − 1)퐬 (1, 푛 − 1) 
 1 + 푃1 from the previous symbols in (8) and (9) are 
 represented by 2(푛 − 1). The strengths of 
 푃2
 +√ ( (푛)퐯 (1, 푛) − (푛)퐯∗(2, 푛)) 2(푛 − 1) can be expressed as a ratio as [1]: 
 1 + 푃 1 1 2 2 2 2
 1 훽 = | 2(푛 − 1)| /| 2(푛)| . (11) 
 +퐳(1, 푛), (8) 
 The second term of (10), i.e. 퐈푖푛푡(, 푛) called 
 ISI components, and the Fig. 3 give that the 
 푃 푃
 ∗ 2 1 ∗ received symbols at the destination have two 
 퐲 (2, 푛) = √ (‖ 2‖퐹 2(푛)퐬(1, 푛)
 1 + 푃1 ISI components. The ISI components of 
 ∗ proposed scheme are reduced in compared to 
 − ‖ 1‖퐹 1(푛)퐬(2, 푛)) 
 the previous DSTC schemes [1, 2] (See Fig. 1 
 푃2푃1 ∗ ∗ in Section 1). It is important that the number of 
 +√ 2(푛 − 1)퐬 (2, 푛) 
 1 + 푃1 ISI components of the proposed scheme always 
 equals two and is independent of the number of 
 푃2 ∗ ∗ ∗ the transmitted relay-antennas. Moreover, the 
 +√ ( 1(푛)퐯1(2, 푛) + 2(푛)퐯2(1, 푛)) 
 1 + 푃1 above analyses show that the TAS technique 
 +퐳∗(2, 푛), (9) not only allows to reduce the requirement of RF 
 The equation (8) and (9) can be rewritten in chains at the relay nodes, but also increases at 
vector form as twice the transmit power at each transmitted 
 antenna as comparison to the previous 
 퐲(1, 푛) cooperative relay networks. However, the 
퐲′(푛) = [ ∗ ] number of feedback bits of the proposed 
 퐲 (2, 푛) scheme is quite larger than the DCL EO-STBC 
 푃2푃1 푃2푃1 scheme. It is a reasonable price for the 
 = √ 퐇퐬′(푛) + √ 퐈i푛푡(푛) advantages of the proposed scheme. 
 1 + 푃1 1 + 푃1
 +퐰(푛), (10) 
 3. Near-Optimumdetection (NOD) 
 where 
 fortheproposedscheme 
 ‖ 1‖퐹 1(푛) ‖ 2‖퐹 2(푛)
 퐇 = [ ∗ ∗ ] ; 
 ‖ 2‖퐹 2(푛) −‖ 1‖퐹 1(푛) As remarked above, although the number of 
 퐬(1, 푛)
 퐬′(푛) = [ ], ISI components have been reduced by using 
 퐬(2, 푛) TAS technique, the ISI components have still 
 existed in the received symbol vector at the 
 T.N. Tran et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 33, No. 1 (2017) 28-36 33 
destination node. The existing ISI components Step 3: Apply the Least Square (LS) at the 
can lead to substantial degradation in system destination to estimate the transmitted signals 
performance. To the end this lack of the from the source node. 
asynchronous cooperative relay network, the As seen the equation (14) 퐲′′(2, 푛) is only 
near-optimum detection (NOD) scheme is related to 퐬(2, 푛). In addition, it can be proved 
employed at the destination node before the that 퐰 (2, 푛) is a circularly symmetric 
information detection. In fact, the symbol Gaussian random variable with zero-mean and 
 2
퐬(1, 푛 − 1) is known through the use of pilot covariance 휎퐖. Assuming the CSI at the 
symbols at the start of the packet. Therefore, the destination node, 퐬̃(2, 푛)can be detected as 
interference components 퐈푖푛푡(1, 푛) = follow 
 ∗
‖ 2‖퐹 2(푛 − 1)퐬 (1, 푛 − 1) in the equation 퐬̃(2, 푛) = arg min |퐲′′(2, 푛)
(10) caneliminate as follows: 퐬(2,푛)∈ 
 Step 1: Remove the ISI components 푃1푃2
 − √ (휆퐬(2, 푛) 
 푃1 + 1
 퐲′(1, 푛) − 퐈 (1, 푛)
 퐲̂(푛) = [ 푖푛푡 ](12) ∗ 2
 퐲′(2, 푛) +Λ(2, 푛)퐬 (2, 푛))| . (16) 
 Step 2: Apply the matched filter by where 퐬(2, 푛) ∈ is possible transmitted 
multiplying the signals removed the ISI symbol. 
components in (12) by 퐇 . Therefore, the Similarly, substituting 퐬̃(2, 푛) back to the 
estimated signals can be represented as equation (15), 퐲′′(1, 푛) also is only related to 
 퐲′′(1, 푛) 퐬(1, 푛). Therefore, 퐬̃(1, 푛) can be detected by 
 퐲′′(푛) = [ ] = 퐇 퐲̂(푛) 퐬̃(1, 푛) = arg min |퐲′′(1, 푛)
 퐲′′(2, 푛) 퐬(1,푛)∈ 
 푃1푃2
 푃1푃2 ∗ − √ (휆퐬(1, 푛) 
 = √ (Δ퐬′(푛) + Λ퐬 (2, 푛)) + 퐰 (푛), 푃 + 1
 푃1+1 1
 (13) +Λ(1, 푛)퐬̃∗(2, 푛))|2. (17) 
 where 퐲′′(1, 푛) and 퐲′′(2, 푛) are given by Due to the presence of the interference 
 component 퐈 (푛) in (10), which will destroy 
 푃 푃 푖푛푡
 퐲′′(2, 푛) = √ 1 2 (휆퐬(2, 푛) the orthogonality of the received signal causing 
 푃1 + 1 a degradation in the system performance when 
 + Λ(2, 푛)퐬∗(2, 푛)) the conventional detector, e.g., the maximum 
 +퐰 (2, 푛), (14) likelihood without interference cancellation, 
 uses at the destination node [1]. However, the 
 푃 푃
 퐲′′(1, 푛) = √ 1 2 (휆퐬(1, 푛) received symbol 퐲′′(2, 푛) in the equation (14) 
 푃1 + 1 has no ISI component via the using NOD. It is 
 + Λ(1, 푛)퐬∗(2, 푛)) noticeable from this equation that the 
 application of the NOD at the destination 
 +퐰 (1, 푛), (15) 
 with effectively removes the interference 
 휆 0 components due to the impact of imperfect 
 Δ = 퐇 퐇 = [ ] ,
 0 휆 synchronous among the relay nodes. 
 2
 2 2
 휆 = ∑ ‖ ‖퐹| (푛)| , 4. Comparisonresults 
 =1
 0 In this section, we present some numerical 
 Λ = 퐇 [ ], 
 ‖ ‖ ∗(푛 − 1)퐬∗(2, 푛) results to demonstrate the performance of our 
 1 퐹 2 proposed cooperative relay network with MRC 
 and 퐰 (푛) = 퐇 퐰(푛). 
 and TAS technique. In all figures, the bit error 
34 T.N. Tran et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 33, No. 1 (2017) 28-36 
rates (BER) are shown as a function of the total transmission rate between the relay and the 
transmit power in the whole network. The destination. 
transmit information symbols are chosen The impact of imperfect synchronization is 
independently and uniformly from QPSK performed by changing the value of 훽 = 0, −6 
constellation. It is assumed that all channels are dB, which means adjusting the effect of 
quasi-static Rayleigh fading channels. The different time delays. Fig. 5 shows the BER 
destination node completely acquires the performance comparisons of the proposed 
channel information states from the source to MRC/TAS DSTC scheme and the previous 
the relays and from the relays to the destination. DCL EO-STBC scheme [1] with the utilizing 
 NOD at the destination node. In this case, the 
 MRC/TAS DSTC scheme has similar 
 configuration network as comparison with DCL 
 EO-STBC scheme [1]. The BER performance 
 of the proposed scheme outweighs the previous 
 cooperative relay network. As shown in Fig. 5, 
 when the BER is 10−3 (at 훽 = −6 dB), the 
 proposed scheme can get an approximate 5 dB 
 gain over the DCL EO-STBC scheme. It could 
 be noticeable that the proposed MRC/TAS 
 DSTC scheme is more robust against the effect 
 Figure 4. BER performance comparison of the asynchronous. 
 of the proposed MRC/TAS and DCL EO-STBC 
 scheme [1] in the perfect synchronous case. 
 Firstly, Fig. 4 illustrates the BER 
performance of the proposed MRC/TAS DSTC 
and DCL EO-STBC scheme [1] in the perfect 
synchronous case where each relay node equips 
two antennas. As seen the Fig. 4, the proposed 
scheme outperforms the previous DCL 
EO-STBC scheme. For example, to achieve a 
BER = 10−3 we need 푃 of ~17 dB for the 
proposed MRC/TAS DSTC scheme and ~21 
dB for the DCL EO-STBC scheme. Secondly, 
the system performance of the MRC/TAS 
 Figure 5. BER performance comparison of the 
DSTC is simulated in the perfect synchronous 
 MRC/TAS DSTC ( 푅 = 2) and the DCL 
assumption and using three antennas at each EO-STBC [1] with the utilizing NOD scheme. 
relay. The left curve of the Fig. 4 shows that the 
system performance of proposed scheme is In order to examine the advantages of 
improved considerably with increasing the increasing the number of the relay-antennas, the 
number of antennas of each relay node. The BER of the proposed scheme is performed with 
improvement of the proposed scheme is three antennas at each relay node and various 
because that our scheme achieves both maximal asynchronous channel conditions. The Fig. 6 
received diversity gain in the first phase and demonstrates that the MRC/TAS DSTC scheme 
cooperative transmit diversity gain in the owning three relay-antennas has greater system 
second phase. Moreover, the proposed scheme performance than, in the similar asynchronous 
has less requirement of RF chains of the relay condition, the DCL EO-STBC one using two 
than the previous works and remains unity antennas at each relay node. For example, at the 
 T.N. Tran et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 33, No. 1 (2017) 28-36 35 
BER of 10−3 (at 훽 = −6 dB), the proposed References 
scheme can obtain about 9 dB gain over the [1] W. Qaja, A. Elazreg, and J. Chambers, 
DCL EO-STBC one. The enhancing “Near-Optimum Detection for Use in Closed-
performance is achieved as the MRC/TAS Loop Distributed Space Time Coding with 
DTSC scheme can get a higher gain including Asynchronous Transmission and Selection of 
both received and transmitted diversity. Two Dual-Antenna Relays," in Proc. Wireless 
 Conference (EW), Guildford, UK, Apr. 2013, 
 pp. 1-6. 
 [2] W. M. Qaja, A. M. Elazreg, and J. A. Chambers, 
 “Distributed Space Time Transmission with 
 Two Relay Selection and Parallel Interference 
 Cancellation Detection to Mitigate 
 Asynchronism," in Proc. European Symposium 
 on Computer Modeling and Simulation (EMS), 
 Valetta, Malta, Nov. 2012, pp. 220-225. 
 [3] Astal M-T EL, Abu-Hudrouss, Ammar M, and 
 Olivier Jan C, “Improved signal detection of 
 wireless relaying networks employing space-time 
 block codes under imperfect synchronization,” 
 Figure 6. BER performance comparison of the Wireless Personal Communications, vol.82, no.1, 
 MRC/TAS DSTC ( 푅 = 3) and the DCL 2015, pp. 533-550. 
 EO-STBC [1] with the utilizing NOD scheme. [4] Alageli, Mahmoud, Aissa Ikhlef, and Jonathon 
 Chambers, “Relay selection for asynchronous 
 AF relay networks with frequency selective 
5. Conclusions channels,” in Proc. Inter. Workshop on Signal 
 Processing Advances in Wireless Communi., 
 Aug. 2016, pp. 1-5. 
 This paper proposes the AF asynchronous 
 [5] Gonzalez, Diana Cristina, Daniel Benevides da 
cooperative relay network using MRC and TAS Costa, and Jose Candido Silveira Santos Filho, 
technique. The use of MRC technique for “Distributed TAS/MRC and TAS/SC Schemes 
combining multiple received symbols is proved for Fixed-Gain AF Systems With Multiantenna 
to obtain maximal received diversity gain in Relay: Outage Performance,” IEEE Transac. on 
compared to conventional DSTC scheme [1,2]. Wireless Communications, vol.15, no.6, 
In the second phase, the TAS technique allows pp.4380-4392, 2016. 
to reduce the ISI components among the relay [6] Y. Jing and B. Hassibi, “Distributed space-time 
 coding in wireless relay networks," IEEE Trans. 
nodes. The analyses and simulation results on Wireless Comm., vol. 5. no. 12, pp. 3524-
demonstrate that the proposed scheme with the 3536, Dec. 2006. 
employment of the NOD works effectively in [7] Desouky, Ahmed, and Ahmed El-Mahdy, 
various synchronization error levels. In other “Asynchronous down-link cooperative 
words, the MRS/TAS DSTC scheme is more communication scheme in Rayleigh fading 
robust against the effect of the asynchronous. wireless environment,” in Proc. Signal Processing: 
The proposed scheme has less requirement of Algorithms, Architectures, Arrangements, and 
RF chains at the relay and exploits the the Applications, 2016, pp.142-146. 
advantage of multi-antennas more effectively in [8] A. Elazreg and A. Kharaz, “Sub-Optimum 
 Detection Scheme for Distributed Closed-Loop 
comparison to the previous one. We believe that Quasi Orthogonal Space Time Block Coding in 
the MRC/TAS DSTC scheme can be useful for Asynchronous Cooperative Two Dual-Antenna 
the distributed relay networks using multi- Relay Networks," in Proc. Wireless Internet, 
antennas at the relay nodes like sensor wireless Lisbon, Portugal, 2015, pp. 217-228. 
network or Ad hoc network under the [9] W. M. Qaja, A. M. Elazreg, and J. A. Chambers, 
asynchronous conditions. “Near-optimum detection scheme with relay 
 selection technique for asynchronous 
36 T.N. Tran et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 33, No. 1 (2017) 28-36 
 cooperative relay networks," IET Comm., vol. 8, [12] J. Harshan and B. S. Rajan, “Co-ordinate 
 no. 8, pp. 1347-1354, May 2014. interleaved distributed space-time coding for 
 [10] B. Kumbhani and R. S. Kshetrimayum, “Error two-antenna-relays networks," IEEE Trans. on 
 performance of two-hop decode and forward Wireless Comm., vol. 8, no. 4, pp. 1783-1791, 
 relaying systems with source and relay transmit Apr. 2009. 
 antenna selection," Electronics Letters, vol. 51, [13] Y. Jing and H. Jafarkhani, “Using Orthogonal 
 no. 6, pp. 530-532, 2015. and Quasi-Orthogonal Designs in Wireless 
 [11] M. T. O. E. Astal and J. C. Olivier, “Distributed Relay Networks," IEEE Trans. on Infor. Theory, 
 Closed-Loop Extended Orthogonal STBC: vol. 53, no. 11, pp. 4106-4118, 2007. 
 Improved performance in imperfect [14] D. A. Gore and A. J. Paulraj, “MIMO antenna 
 synchronization," in Proc. Personal Indoor and subset selection with space-time coding," IEEE 
 Mobile Radio Communications (PIMRC), Trans. on Signal Processing, vol. 50, no. 10, pp. 
 London, England, Sept. 2013, pp. 1941-1945. 2580-2588, 2002. 
G 
h