Hydraulic flow unit classification from core data: Case study of the Z gas reservoir, Poland

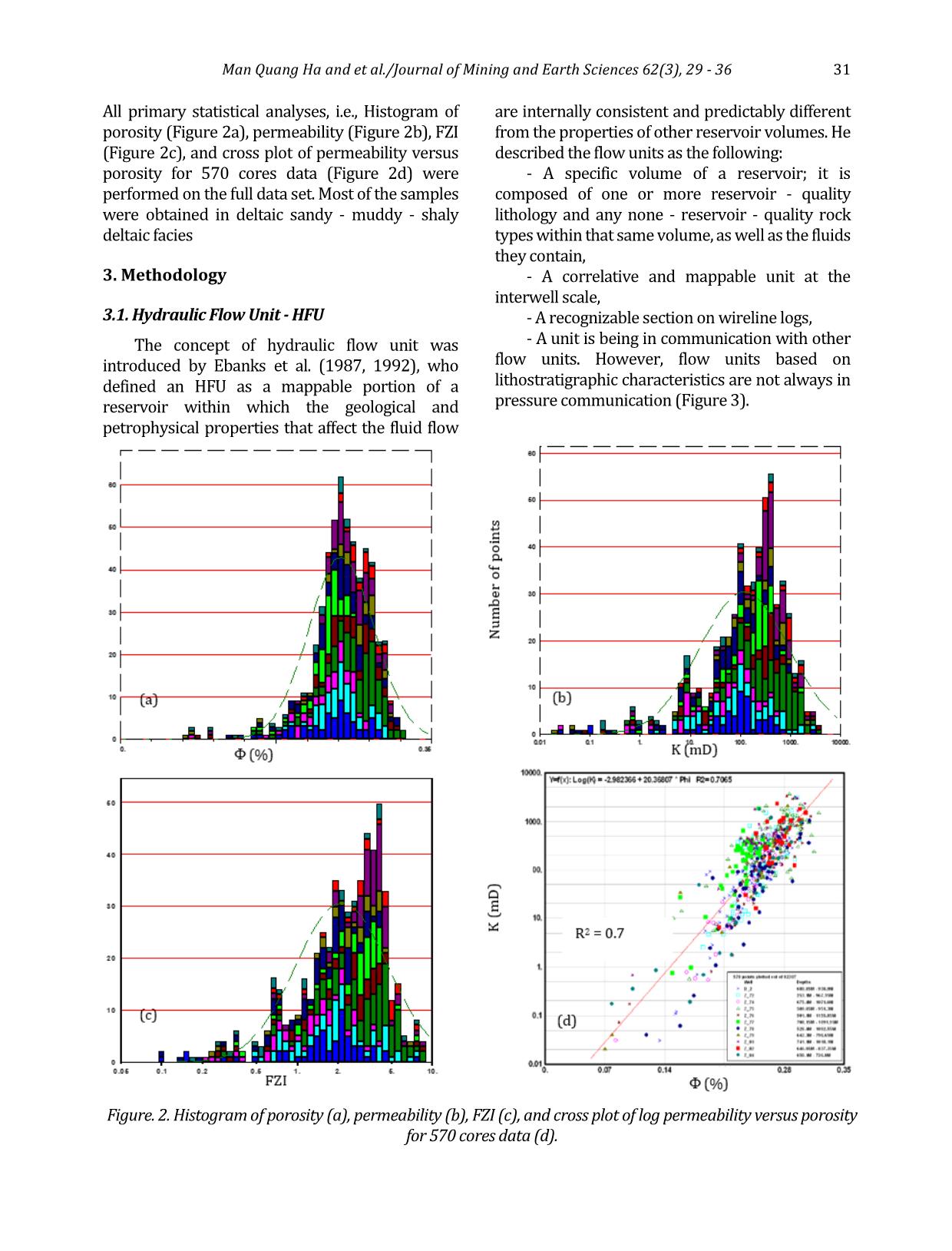
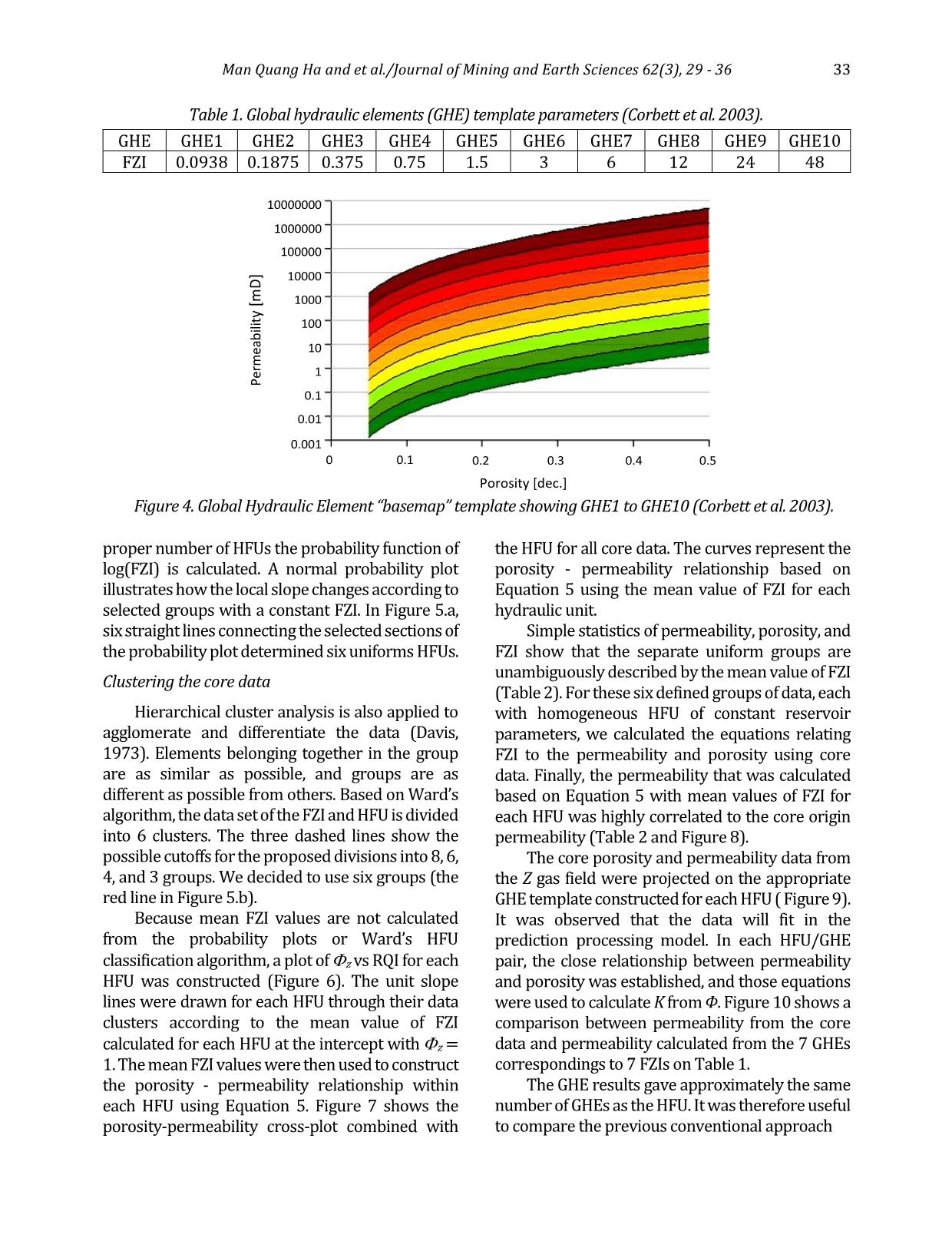
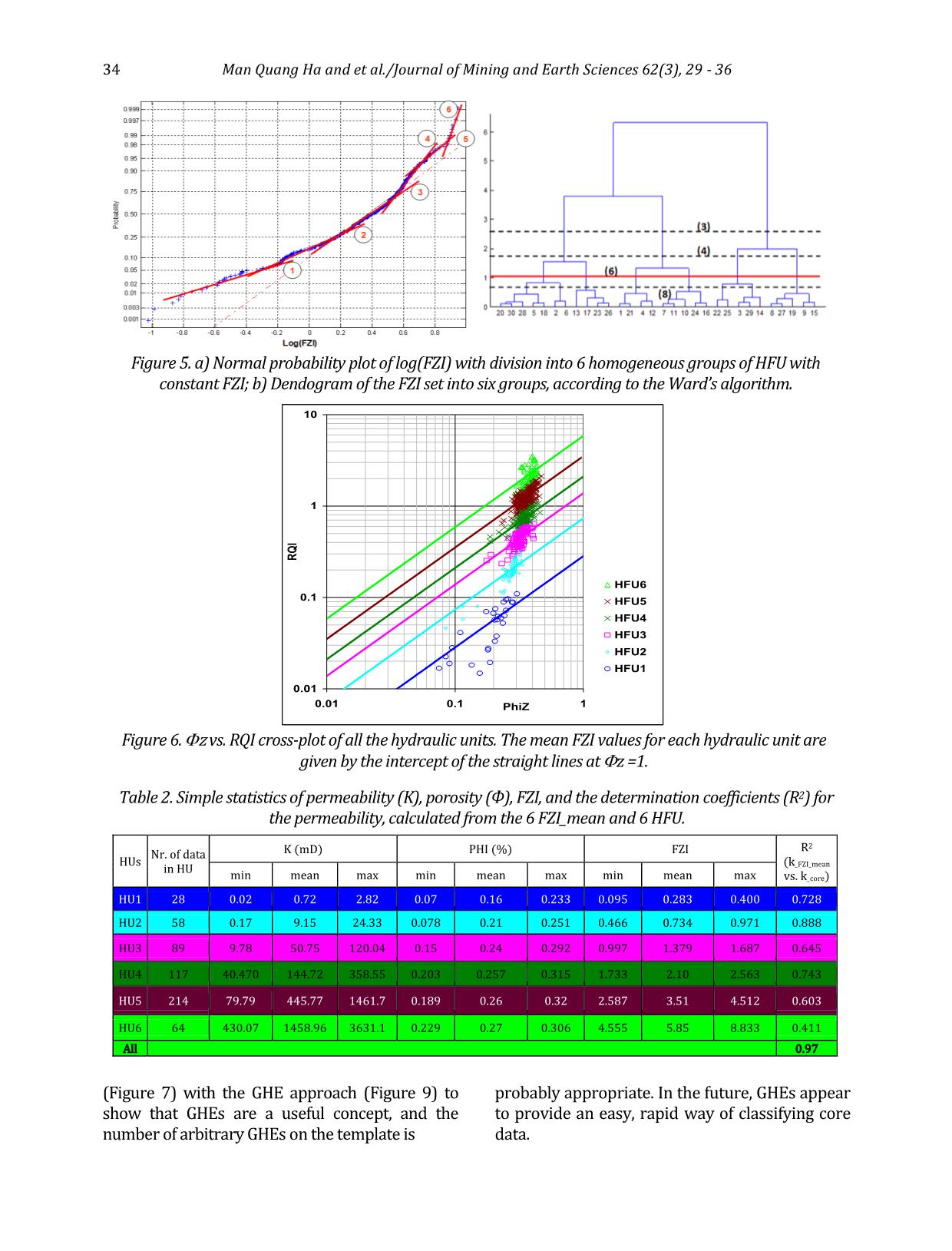
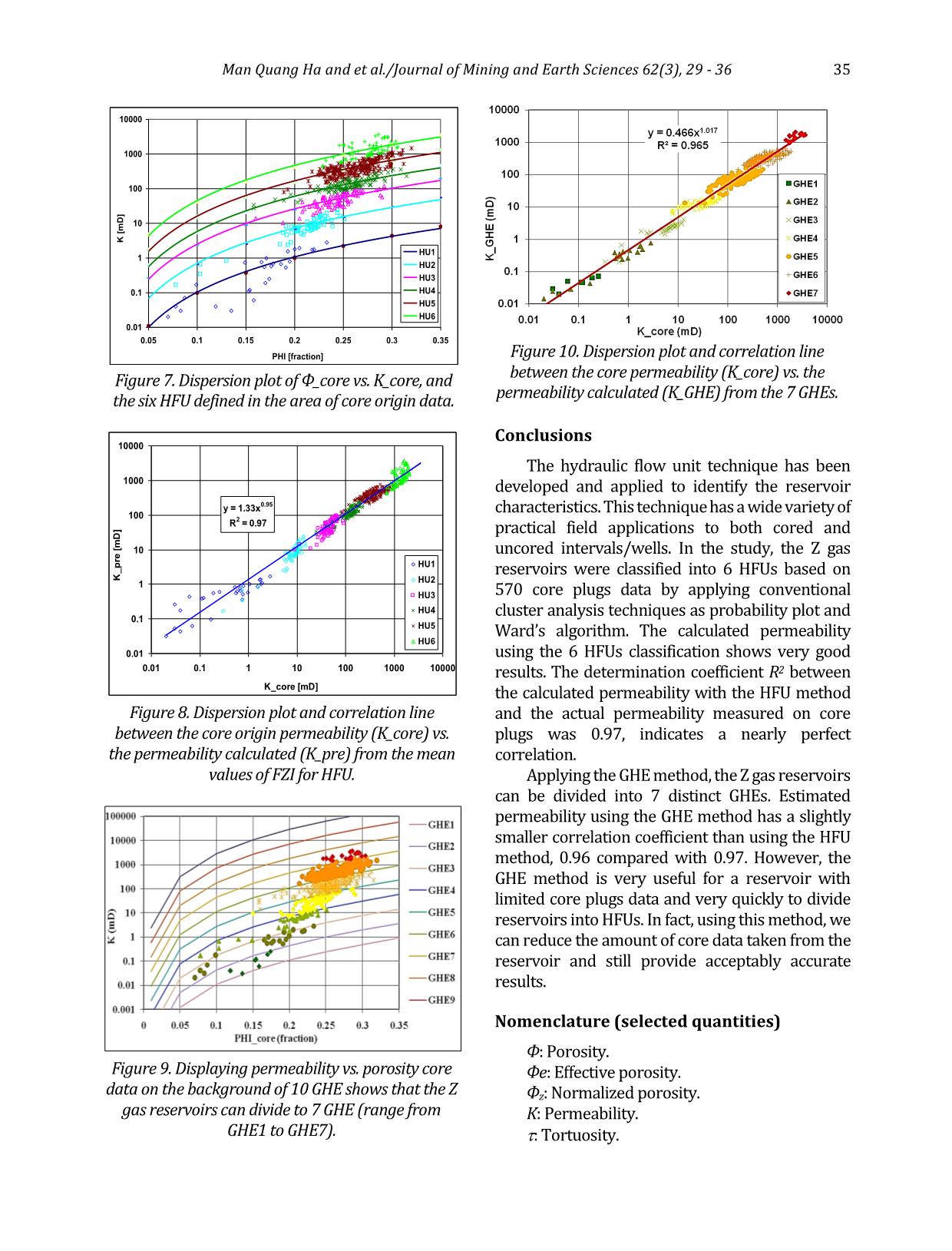
d with the 11 wells location (after Mysliwiec, 2006; Mysliwiec et al., 2004). 
 Man Quang Ha and et al./Journal of Mining and Earth Sciences 62(3), 29 - 36 31 
All primary statistical analyses, i.e., Histogram of 
porosity (Figure 2a), permeability (Figure 2b), FZI 
(Figure 2c), and cross plot of permeability versus 
porosity for 570 cores data (Figure 2d) were 
performed on the full data set. Most of the samples 
were obtained in deltaic sandy - muddy - shaly 
deltaic facies 
3. Methodology 
3.1. Hydraulic Flow Unit - HFU 
The concept of hydraulic flow unit was 
introduced by Ebanks et al. (1987, 1992), who 
defined an HFU as a mappable portion of a 
reservoir within which the geological and 
petrophysical properties that affect the fluid flow 
are internally consistent and predictably different 
from the properties of other reservoir volumes. He 
described the flow units as the following: 
- A specific volume of a reservoir; it is 
composed of one or more reservoir - quality 
lithology and any none - reservoir - quality rock 
types within that same volume, as well as the fluids 
they contain, 
- A correlative and mappable unit at the 
interwell scale, 
- A recognizable section on wireline logs, 
- A unit is being in communication with other 
flow units. However, flow units based on 
lithostratigraphic characteristics are not always in 
pressure communication (Figure 3). 
Figure. 2. Histogram of porosity (a), permeability (b), FZI (c), and cross plot of log permeability versus porosity 
for 570 cores data (d). 
32 Man Quang Ha and et al./Journal of Mining and Earth Sciences 62(3), 29 - 36 
The structure, texture, and mineral 
composition of rock formation strongly influence 
the relationship between porosity and 
permeability. Petrophysicists working for the oil 
and gas industry and prospecting hydrogeology 
and geothermal water reserves prospecting try to 
find the best relationship between those two 
reservoir parameters since the times of Kozeny 
(1927) and Carman (1937). A breakthrough was 
noted with an approach based on the FZI proposed 
by Amaefule et al. (1993), which was then followed 
by other authors (Prasad, 2000). FZI is a derivative 
factor determined based on the generalized 
Cozeny - Carman equation: 
gvs SF
k
222
e
e
3 1
-1 

(1) 
where: K - the permeability; Φe - the effective 
porosity; Fs - the shape factor; τ - the tortuosity of 
pores; Sgv - the specific surface. 
Amaefule et al. (1993) introduced two 
auxiliary factors: Φz, the normalized porosity 
(Equation 2), and RQI, the reservoir quality index 
(Equation 3). This results in a new formula 
(Equation 4), which is a definition of FZI. 
The basis of HFU classification is to identify 
groups of data that form the unit - slope straight 
lines on a log - log plot of RQI versus z. The 
permeability of a sample point is then calculated 
from a pertinent HFU using the mean FZI value and 
the corresponding sample porosity using the 
following Equation (5). 
e
e
z 


1
(2) 
e
k
RQI

0314.0 
(3) 
zgvs
RQI
SF
FZI

1
(4) 
2
3
2
)1(
)(24.1014
e
eFZIK
 

(5) 
On the basis of Equations (Equation 1÷4), we 
assume that units of constant FZI have invariable 
reservoir parameters that differ from the 
surrounding neighbourhood. Proper division of 
the data set into units of constant FZI forms the 
basis for the HFU construction, resulting in the best 
partial relationships of permeability vs porosity for 
each HFU. 
3.2. Global Hydraulic Elements - GHE 
Corbett et al. (2003, 2004) proposed the rapid 
and more straightforward approach to plot the 
porosity and permeability data on the 
predetermined global hydraulic elements (GHE) 
template ( Figure 4), which is constructed based on 
eq. (5). A systematic series of a priori FZI values 
were arbitrarily chosen to define 10 porosity - 
permeability elements. Only ten were chosen to 
split the wide range of porosity and permeability 
parameter space into a manageable number of 
GHEs (Table 1). 
Data in the study projected on the Corbett and 
Potter (2004) template shows the close 
relationship between permeability and porosity in 
each HFU = GHE. Thus, established equations are 
used to calculate K from Φ and FZI. The 
relationship between permeability from the core 
data and permeability calculated from the means of 
FZIs in GHE is very close (Figure 4). 
4. Results and discussions 
Probability function to select number of HFU 
To confirm the division of the data set into the 
Figure 3. Various parameters are used in defining 
geologic flow units; the flow units are defined based 
on lithofacies, pore types, porosity, and permeability 
cross - plots, capillary pressure measurements, and 
gamma - ray log response (after Ebanks et al. 1992). 
 Man Quang Ha and et al./Journal of Mining and Earth Sciences 62(3), 29 - 36 33 
GHE GHE1 GHE2 GHE3 GHE4 GHE5 GHE6 GHE7 GHE8 GHE9 GHE10 
FZI 0.0938 0.1875 0.375 0.75 1.5 3 6 12 24 48 
proper number of HFUs the probability function of 
log(FZI) is calculated. A normal probability plot 
illustrates how the local slope changes according to 
selected groups with a constant FZI. In Figure 5.a, 
six straight lines connecting the selected sections of 
the probability plot determined six uniforms HFUs. 
Clustering the core data 
Hierarchical cluster analysis is also applied to 
agglomerate and differentiate the data (Davis, 
1973). Elements belonging together in the group 
are as similar as possible, and groups are as 
different as possible from others. Based on Ward’s 
algorithm, the data set of the FZI and HFU is divided 
into 6 clusters. The three dashed lines show the 
possible cutoffs for the proposed divisions into 8, 6, 
4, and 3 groups. We decided to use six groups (the 
red line in Figure 5.b). 
Because mean FZI values are not calculated 
from the probability plots or Ward’s HFU 
classification algorithm, a plot of z vs RQI for each 
HFU was constructed (Figure 6). The unit slope 
lines were drawn for each HFU through their data 
clusters according to the mean value of FZI 
calculated for each HFU at the intercept with z = 
1. The mean FZI values were then used to construct 
the porosity - permeability relationship within 
each HFU using Equation 5. Figure 7 shows the 
porosity-permeability cross-plot combined with 
the HFU for all core data. The curves represent the 
porosity - permeability relationship based on 
Equation 5 using the mean value of FZI for each 
hydraulic unit. 
Simple statistics of permeability, porosity, and 
FZI show that the separate uniform groups are 
unambiguously described by the mean value of FZI 
(Table 2). For these six defined groups of data, each 
with homogeneous HFU of constant reservoir 
parameters, we calculated the equations relating 
FZI to the permeability and porosity using core 
data. Finally, the permeability that was calculated 
based on Equation 5 with mean values of FZI for 
each HFU was highly correlated to the core origin 
permeability (Table 2 and Figure 8). 
The core porosity and permeability data from 
the Z gas field were projected on the appropriate 
GHE template constructed for each HFU ( Figure 9). 
It was observed that the data will fit in the 
prediction processing model. In each HFU/GHE 
pair, the close relationship between permeability 
and porosity was established, and those equations 
were used to calculate K from Φ. Figure 10 shows a 
comparison between permeability from the core 
data and permeability calculated from the 7 GHEs 
correspondings to 7 FZIs on Table 1. 
The GHE results gave approximately the same 
number of GHEs as the HFU. It was therefore useful 
to compare the previous conventional approach 
1000000
100000
10000
1000
100
10
1
0.1
0.01
0.001
10000000
P
er
m
ea
b
ili
ty
 [
m
D
]
Porosity [dec.]
0 0.1 0.2 0.3 0.4 0.5
Figure 4. Global Hydraulic Element “basemap” template showing GHE1 to GHE10 (Corbett et al. 2003). 
Table 1. Global hydraulic elements (GHE) template parameters (Corbett et al. 2003). 
34 Man Quang Ha and et al./Journal of Mining and Earth Sciences 62(3), 29 - 36 
(Figure 7) with the GHE approach (Figure 9) to 
show that GHEs are a useful concept, and the 
number of arbitrary GHEs on the template is
probably appropriate. In the future, GHEs appear 
to provide an easy, rapid way of classifying core 
data.
Figure 5. a) Normal probability plot of log(FZI) with division into 6 homogeneous groups of HFU with 
constant FZI; b) Dendogram of the FZI set into six groups, according to the Ward’s algorithm. 
0.01
0.1
1
10
0.01 0.1 1PhiZ
R
Q
I
HFU6
HFU5
HFU4
HFU3
HFU2
HFU1
Figure 6. z vs. RQI cross-plot of all the hydraulic units. The mean FZI values for each hydraulic unit are 
given by the intercept of the straight lines at z =1. 
HUs 
Nr. of data 
in HU 
K (mD) PHI (%) FZI R2 
(k_FZI_mean 
vs. k_core) min mean max min mean max min mean max 
HU1 28 0.02 0.72 2.82 0.07 0.16 0.233 0.095 0.283 0.400 0.728 
HU2 58 0.17 9.15 24.33 0.078 0.21 0.251 0.466 0.734 0.971 0.888 
HU3 89 9.78 50.75 120.04 0.15 0.24 0.292 0.997 1.379 1.687 0.645 
HU4 117 40.470 144.72 358.55 0.203 0.257 0.315 1.733 2.10 2.563 0.743 
HU5 214 79.79 445.77 1461.7 0.189 0.26 0.32 2.587 3.51 4.512 0.603 
HU6 64 430.07 1458.96 3631.1 0.229 0.27 0.306 4.555 5.85 8.833 0.411 
All 0.97 
Table 2. Simple statistics of permeability (K), porosity (Ф), FZI, and the determination coefficients (R2) for 
the permeability, calculated from the 6 FZI_mean and 6 HFU. 
 Man Quang Ha and et al./Journal of Mining and Earth Sciences 62(3), 29 - 36 35 
Conclusions 
The hydraulic flow unit technique has been 
developed and applied to identify the reservoir 
characteristics. This technique has a wide variety of 
practical field applications to both cored and 
uncored intervals/wells. In the study, the Z gas 
reservoirs were classified into 6 HFUs based on 
570 core plugs data by applying conventional 
cluster analysis techniques as probability plot and 
Ward’s algorithm. The calculated permeability 
using the 6 HFUs classification shows very good 
results. The determination coefficient R2 between 
the calculated permeability with the HFU method 
and the actual permeability measured on core 
plugs was 0.97, indicates a nearly perfect 
correlation. 
Applying the GHE method, the Z gas reservoirs 
can be divided into 7 distinct GHEs. Estimated 
permeability using the GHE method has a slightly 
smaller correlation coefficient than using the HFU 
method, 0.96 compared with 0.97. However, the 
GHE method is very useful for a reservoir with 
limited core plugs data and very quickly to divide 
reservoirs into HFUs. In fact, using this method, we 
can reduce the amount of core data taken from the 
reservoir and still provide acceptably accurate 
results. 
Nomenclature (selected quantities) 
Ф: Porosity. 
Фe: Effective porosity. 
Фz: Normalized porosity. 
K: Permeability. 
: Tortuosity. 
0.01
0.1
1
10
100
1000
10000
0.05 0.1 0.15 0.2 0.25 0.3 0.35
PHI [fraction]
K
 [
m
D
]
HU1
HU2
HU3
HU4
HU5
HU6
y = 1.33x
0.95
R
2
 = 0.97
0.01
0.1
1
10
100
1000
10000
0.01 0.1 1 10 100 1000 10000
K_core [mD]
K
_
p
re
 [
m
D
]
HU1
HU2
HU3
HU4
HU5
HU6
Figure 7. Dispersion plot of Ф_core vs. K_core, and 
the six HFU defined in the area of core origin data. 
Figure 8. Dispersion plot and correlation line 
between the core origin permeability (K_core) vs. 
the permeability calculated (K_pre) from the mean 
values of FZI for HFU. 
Figure 9. Displaying permeability vs. porosity core 
data on the background of 10 GHE shows that the Z 
gas reservoirs can divide to 7 GHE (range from 
GHE1 to GHE7). 
Figure 10. Dispersion plot and correlation line 
between the core permeability (K_core) vs. the 
permeability calculated (K_GHE) from the 7 GHEs. 
36 Man Quang Ha and et al./Journal of Mining and Earth Sciences 62(3), 29 - 36 
Sgr: Specific surface area per unit grain. 
RQI: Reservoir Quality Index. 
FZI: Flow Zone Index. 
GHE: Global Hydraulic Element. 
HFU: Hydraulic Flow Unit. 
Author contributions 
The first author, Man Ha Quang, built up 
conception, data analysis and draft the article. The 
second author, Anh Le Ngoc contributed to the 
methodology and Jadwiga Jarzyna author give a 
critical review for the final version to be submitted. 
References 
Amaefule, J. O., Altunbay, M., Tiab, D., Kersey, D. G., 
and Keelan, D. K., (1993). Enhanced reservoir 
description: Using core and log data to identify 
hydraulic (flow) units and predict 
permeability in uncored intervals/wells: SPE 
Paper 26436. 205 - 220. 
Carman, P. C., (1937). Fluid Flow through 
Granular Beds: Trans. AIChE 15. 150 - 166. 
Corbett P., Ellabard Y., Mohhammed K., (2003). 
Global Hydraulic Elements - Elementary 
Petrophysics for Reduced Reservoir Modeling: 
EAGE 65th Conference and Exhibition, 
Stavanger paper F. 26. 
Corbett P. W. M. and Potter D. K., (2004). 
Petrotyping: a basemap and atlas for 
navigating through permeability and porosity 
data for reservoir comparison and 
permeability prediction: Paper prepared for 
presentation at the international symposium of 
the Society of Core Analysts held in Abu Dhabi, 
UAE, 5 - 9 October. 1 - 12. 
Davis, J. C., (1973). Statistics and data analysis in
geology: John Wiley & Sons, INC. 
Ebanks W. J., (1987). Flow unit concept - 
integrated approach for engineering projects. 
Abstract presented June 8, during the 
roundtable sessions at the 1987 American 
Association of Petroleum Geologists Annual 
Convention. 
Ebanks, W. J. Jr., Scheiling, M. H., Atkinson, C. D., 
(1992). Flow units for reservoir 
characterization. In: D. Morton - Thompson, 
A.M. Woods (Eds.), Development Geology 
Reference Manual, Amer. Assoc. Petrol. Geol. 
Methods in Exploration Series No. 10. 282 - 284. 
Kozeny, J., (1927). Uber Kapillare Letung des 
Wassers im Boden, Sitzungsberichte: Royal 
Academy of Science, Vienna, Proc. Class I 136. 
271 - 306. 
Matyasik I., Mysliwiec M., Lesniak G., Such P., 
(2007). Relationship between Hydrocarbon 
Generation and Reservoir Development in the 
Carpathian Foreland: Chapter 22 - Frontiers in 
Earth Science: Thrust Belt and Foreland Basin 
From Fault Kinetics to Hydrocarbon System, 
Springer. 
Mysliwiec M., (2006). Types of the Miocene 
reservoir rocks (Zołynia - LeZajsk gas field) 
and the methods of the gas reserves 
estimation: Nafta - Gaz 62(4). 139 - 150 (in 
Polish, abstract in English). 
Mysliwiec M., Madej K., Bys I., (2004). The 
Miocene gas fields discovered in the Rzeszów 
area, Carpathian Foredeep, on the base of the 
Direct Hydrocarbon Indicators: Przegląd 
Geologiczny 52(7). 501 - 506 (in Polish, 
Abstract in English).