Giáo trình môn Chương trình dịch (Phần 2)
ĐỊNH NGHĨA CÚ PHÁP ĐIỀU KHIỂN.
Cú pháp điều khiển (syntax-directed definition) là một dạng tổng quát hoá của
văn phạm phi ngữ cảnh, trong đó mỗi ký hiệu văn phạm có một tập thuộc tính đi
kèm, được chia thành 2 tập con là thuộc tính tổng hợp (synthesized attribute) và
thuộc tính kế thừa (inherited attribute) của ký hiệu văn phạm đó.
Một cây phân tích cú pháp có trình bày các giá trị của các thuộc tính tại mỗi
nút được gọi là cây phân tích cú pháp có chú giải (hay gọi là cây phân tích đánh
dấu) (annotated parse tree).
2.1. Cú pháp điều khiển.
2.1.1. Dạng của định nghĩa cú pháp điều khiển.
Trong mỗi cú pháp điều khiển, mỗi sản xuất A->α có thể được liên kết với
một tập các qui tắc ngữ nghĩa có dạng b = f(c1, . . .,ck) với f là một hàm và
a) b là một thuộc tính tổng hợp của A, còn c1, . . .,ck là các thuộc tính của các ký
hiệu trong sản xuất đó. Hoặc
b) b là một thuộc tính kế thừa của một trong những ký hiệu ở vế phải của sản
xuất, còn c1, . . . ,ck là thuộc tính của các ký hiệu văn phạm.Ta nói là thuộc tính b phụ thuộc vào các thuộc tính c1, . . .,ck.
- Một văn phạm thuộc tính (Attribute Grammar) là một cú pháp điều khiển
mà các luật ngữ nghĩa không có hành động phụ.
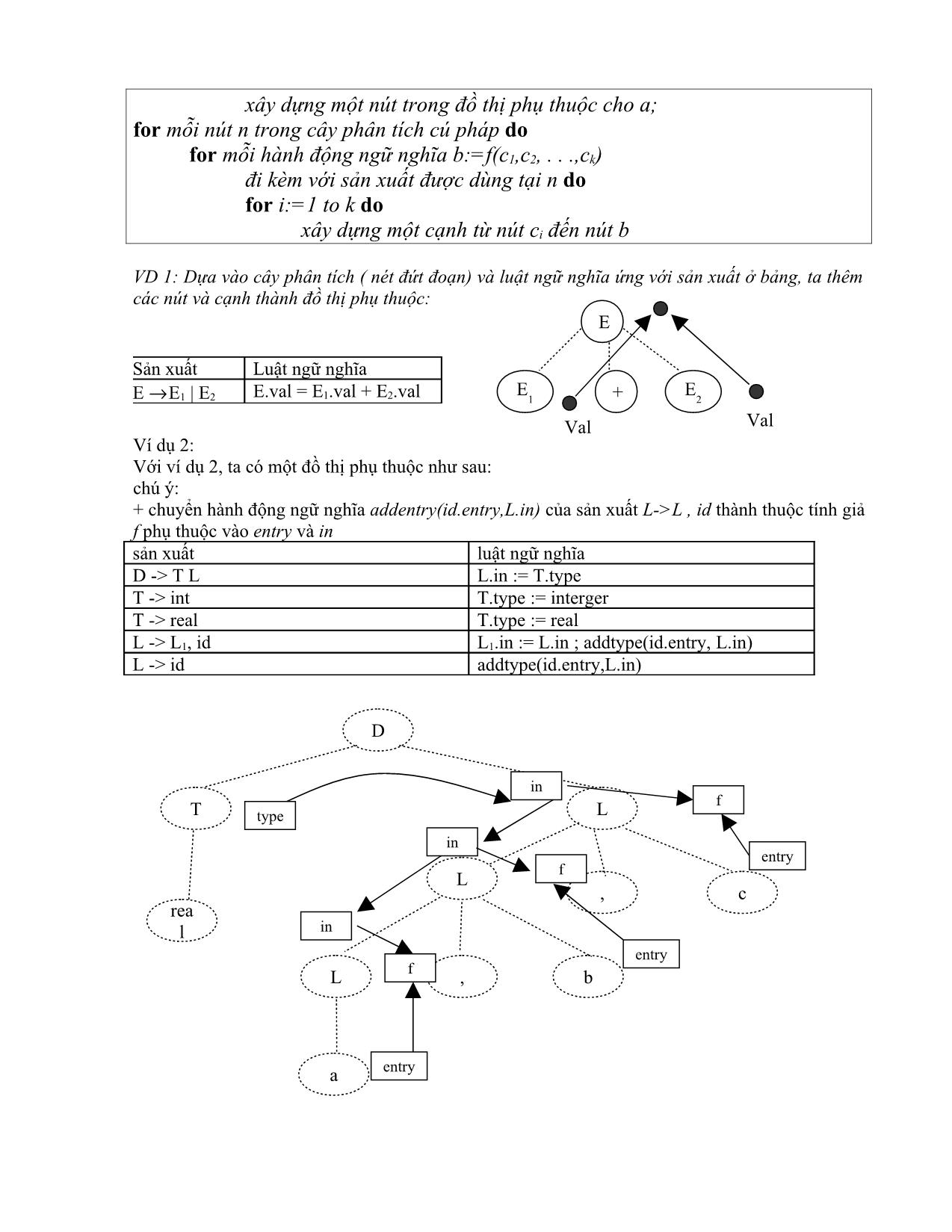
Ví dụ: Sau đây là văn phạm cho một chương trình máy tính bỏ túi với val là một
thuộc tính biểu diễn giá trị của ký hiệu văn phạm.
Sản xuất Luật ngữ nghĩa
L -> E n Print(E.val)
E -> E1 + T E.val = E1.val + T.val
E -> T E.val = T.val
T -> T1 * F T.val = T1.val * F.val
T -> F T.val = F.val
F -> ( E ) F.val = E.val
F -> digit F.val = digit.lexval
Từ tố digit có thuộc tính Lexval: là giá trị của digit đó được tính nhờ bộ phân tích từ vựng. Kí
hiệu n : xuống dòng, Print : in kết quả ra màn hình.
2.1.2. Thuộc tính tổng hợp.
Trên một cây phân tích, thuộc tính tổng hợp được tính dựa vào các thuộc ở
các nút con của nút đó, hay nói cách khác thuộc tính tổng hợp được tính cho các ký
hiệu ở vế trái của sản xuất và tính dựa vào thuộc tính của các ký hiệu ở vế phải.
Một cú pháp điều khiển chỉ sử dụng các thuộc tính tổng hợp được gọi là cú
pháp điều khiển thuần tính S (S-attribute definition).
Một cây phân tích cho văn phạm cú pháp điều khiển thuần tính S có thể thực
hiện các luật ngữ nghĩa theo hướng từ lá đến gốc và có thể sử dụng trong phương
pháp phân tích LR.
Ví dụ: vẽ cây cho đầu vào: 3*4+4n

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Giáo trình môn Chương trình dịch (Phần 2)

You are asked the count the number of constants (CONS), variables (VAR) and
MOPER in an expression. Insert action symbols in the grammar described before Question 2,
explain what semantic actions they trigger and what each semantic action does.
(20 points)
Regular Expressions
Question 1: Consider the concept of “closure”. A set S is said to be closed under a (binary)
operation ⊕ if and only if applying the operation to two elements in the set results in another
element in the set. For example, consider the set of natural numbers N and the “+” (addition)
operation. If we add any two natural numbers, we get a natural number. Formally x, y are
elements of N implies x + y is an element of N. State true or false and explain why
a. Only infinite sets (sets with infinite number of elements, like the set of natural numbers)
can be closed
b. Infinite sets are closed under all operations
c. The set [a-z]* is closed under concatenation operation
Question 2:
For each of the regular expressions below, state if they describe the same set of strings (state if
they are equivalent). If they are equivalent, what is the string they describe?
1. [a-z][a-z]* and [a-z]+
2. [a-z0-9]+ and [a-z]+[0-9]+
3. [ab]?[12]? and a1|b1|a2|b2
4. [ab12]+ and a|b|1|2|[ab12]*
5. [-az]* and [a-z]*
6. [abc]+ and [cba]+
7. [a-j][k-z] and [a-z]
Question 3:
For each of the strings described below, write a regular expression that describes them and draw a
finite automaton that accepts them.
1. 1. The string of zero or more a followed by three b followed zero or more c
2. 2. The string of zero or more a, b and c but every a is followed by two or
more b
3. 3. All strings of digits that represent even numbers
4. 4. All strings of a’s and b’s that contain no three consecutive b’s.
5. 5. All strings that can be made from {0, 1} except the strings 11 and 111
Question 1: Pumping Lemma and Regular Languages
You can use the pumping lemma and the closure of the class of regular
languages under
union, intersection and complement to answer the following question. Proofs
should be
rigorous. Note that for each of the questions below, you may or may not have
to use the
pumping lemma.
Note that the notation 0m means “0 repeated m times”. So the language of
strings of the
form 0m such that m ¡Ý 0 would contain strings like the null string 0, 00, 000,
(this is
[0]*. Whereas the language of strings of the form 0m such that m ¡Ý 1 would
be [0]+)
a. Is the language of strings of the form 0m1n0m such that m, n ¡Ý 0 regular? If
it is regular,
prove that it is regular. If it is not regular, prove that is not regular. Note
that, a rigorous
proof is needed. General reasoning or explanations that are not rigorous will
not get full
credit. (15 points)
b. Consider a language whose alphabet is from the set {a, b}. Is the
language of
palindromes over this alphabet regular? If it is regular, prove that it is
regular. If it is not
regular, prove that is not regular. Note that, a rigorous proof is needed.
General reasoning
or explanations that are not rigorous will not get full credit. (15 points)
Hint: A palindrome is a word such that when read backwards, is the same
word. For
example the word “mom” when read left to right is the same as it is when it
is read right
to left. In general, the first half, when reversed, yields the second half. If the
length of the
string is odd, the middle character is left as it is. For example, consider the
word
“redivider”. Reversing “redi” yields “ider” and “v” is left as it is. For strings
with
alphabet {a, b}, “aaabaaa” is a palindrome but “abaaa” is not.
c. A language, whose alphabet is {a, b}, such that the strings of the
language contain
equal number of “ab” and “ba”. Note that “aba” is part of the language,
because the first
letter and the second letter form “ab” and the second and third form “ba”. Is
this language
regular? If it is regular, prove that it is regular. If it is not regular, prove that
is not
regular. Note that, a rigorous proof is needed. General reasoning or
explanations that are
not rigorous will not get full credit. (15 points)
d. The class of regular languages is closed under union. That is of A is a
regular language
and B is a regular language, then C is a regular language, where C = A . B.
Note that B
. C. (B is a subset of C). Let D be some subset of C (that is, D . C). In general,
is D
regular? If it is regular, prove that it is regular. If it is not regular, prove that
is not
regular. Note that, a rigorous proof is needed. General reasoning or
explanations that are
not rigorous will not get full credit. (15 points)
Question 2:
Consider the language described by the regular expression a+b*a, the set of
all strings
that has one or more a’s followed by zero or more b’s and ending in a single
a.
a. Construct a NFA which recognizes this language. Note that you need to
construct a
primitive NFA using the constructions describe in class. (10 points)
b. Convert the above NFA to a DFA using . closure. Clearly indicate the steps
of .
closure. (20 points)
c. Convert the above DFA to an optimized DFA (10 points)
HomeWork
1. Work on the homework individually. Do not collaborate or copy from others
2. The homework is due on Tuesday, April 24 In Class. No late submissions
will be entertained
3. Do not email your answers to either the Professor or the TA. Emailed
answers will not be
considered for evaluation
Question 1. (50 Points)
Consider the following grammar. Construct LR(0) items, DFA for this grammar
showing LR(0) shiftreduce
table. Is this grammar LR(0)? Indicate all possible shift-reduce as well as
reduce-reduce
conflicts. Using the concept of look-ahead, generate SLR(1) table – which
LR(0) conflicts get
eliminated? Using the input (ID + ID) * ID show the SLR(1) parse - show the
stack states and shifts
and reductions as shown in the examples in the Louden book.
Grammar:
E' -> E
E -> E + T
E -> T
T -> T * ID
T -> ID
T -> (E)
Question 2. (50 Points)
Construct a pushdown automaton for the following language:
L = { aibjck | i, j, k >= 0, either i = j or j = k}
Practice
Q #1. Design a Turing machine for recognizing the language (please give a
formal
description including tape alphabet, full state transition diagram identifying
the
acceptance and rejection states if any)
L = {an bn cn | n >= 0}
L = { w | w contains twice as many 0's as 1's, w is made from {0,1}* }
Q #2. Design a Turing machine to perform multiplication of two natural
numbers
represented as the number of zeroes. For example, number five is
represented as 00000
Hint: Use repeated addition
Q #3 Design LR(0) items, their DFA and SLR(1) parse table for the following
grammar
showing the parse for the following input : ((a), a, (a, a)) Also show the parse
tree
obtained. Is this a LR(0) grammar? If not show the conflicts and show how
you can
resolve them through SLR(1) construction
Grammar :
E -> (L)| a
L -> L, E| E
Q #4 Design Context free grammars for the following languages (alphabet is
{0,1})
a. {w | w starts and ends with the same symbol (either 0 or 1, which is the
alphabet)}
b. {w | w = wr ie, w is a palindrome}
c. {ai bj ck | i = j or j = k, i, j, k >= 0}
Q #5 Design pushdown automata (PDA) for the following language:
{w | w has odd length and the middle character is 0}
Q #6 Show first, follow and predict sets for the following grammar after
removing left
recursion and left factoring:
E -> E + T
E -> T
T -> T * P
T -> P
P -> (E)
P -> ID
Q # 7 Using the pumping lemma show that the following languages are not
regular:
{0m 1n | m not equal to n}
{02n
| n >= 0}
Q #8 Design NFA, DFA and minimize the DFA for the regular expression:
0*1*0*0
Test 1
Question 1: DFAs (Choose any three questions out of five: 30 points)
Devise DFAs for:
1. All strings that start with 1 must end with a 0 and those which start with
0 must end with 1 (alphabet of this language is {0,1}), no null string
2. All strings from the alphabet {a, b} which contain an odd number of a’s
and even (but non-zero) number of b’s
3. All strings that must have 0110 as the substring (alphabet {0,1})
4. All strings which have a length greater than or equal to 3 and ending on
b or two consecutive a’s
5. Strings that do not contain 3 consecutive a’s
Question 2: Regular expressions (Choose any three questions out of
five: 30 points)
Write regular expressions for:
1. Expressions that enumerate all positive integers (including 0) upto 100000
but without any leading zeroes
2. Strings made from {a, b} that start and end on the same letter (ie, strings
starting with a end on a and those starting with b end on b)
3. Floats using decimal point representation with integer and fractional parts
– no leading or trailing zeros and precision upto 4 places after decimal
4. Identifiers that start with a digit or lowercase letter following which one
can optionally have one or more of digits or letters or underscores.
Identifiers can not end on an underscore (consecutive underscores ok
though)
5. Positive integers no leading zeros in which all 2’s should occur only after
3’s and all 1’s should occur only after 2’s (ie, no 2 should occur before a 3
or no 1 should occur before a 2).
Question 3: Regular Expression . NFA . DFA (30 points)
Convert the following regular expression into a NFA and convert the NFA to
DFA
showing the key steps (such as computing å-closures of sets of states etc.) :
b[ab]* Show
all possible NFA transitions (using parallel tree) for the string babba and
verify the state
transitions in corresponding DFA
Question 4: State True or False (10 points)
a. Consider a language S=(a|b)*. Consider a Regular Language L, whose
alphabet is
from the set .= {a, b}. Let M be a DFA that Recognizes L. Let M' be a DFA
obtained from M by changing all accepting states of the M into non-accepting
states, and by changing all non-accepting states of M to accepting states. M'
recognizes the complement of language L given by S – L
b. For every NFA and its equivalent DFA, the number of states in equivalent
DFA
must be at least equal to the number of states in the NFA.
c. Consider languages L and L’ such that L . L’. Let M be a DFA that
recognizes L
and M’ be DFA that recognizes L’ then the number of states in M’ must be
equal
to or greater than those in M.
d. Consider languages L and L’ such that L . L’. Let M be a DFA that
recognizes L
and M’ be DFA that recognizes L’ then the number of states in M’ must be
lesser
than or equal to those in M.
e. For every regular expression there can exist more than one DFA that
recognizes
the language described by the regular expression.
.
Tesst 2
Project
Notes:
1. This project has two phases. Phase 1 is due by April 14th by 5pm. Phase 2
is due by April 28th
by 5pm.
2. There will be no extensions for either phases
3. You will work in groups of three
4. Each group should submit a report and source code for each phase. If
multiple source files, they
must be tarred along with the makefile
5. You can program in C, C++ or Java. Do not use tools (like lex and yacc) or
the standard
template library
6. Code should be properly documented with meaningful variable and
function names. Short
elegant code will get bonus points.
7. You will find the course slides on DFA/NFA/scanner/recursive descent
parser useful.
8. Each phase of the project is worth 100 points. The bonus section is worth
50 points.
Phase 1:
Objective: To write a scanner and parser which can construct and execute an
NFA for any regular
expression.
Consider the language of regular expressions. The alphabet of this language
is the set {a, b, *,
+, (, ), ., |} (commas and spaces are not part of the language). Using
this alphabet one can
write any regular expression. Our goal in this project is to be able to read any
regular expression
described by the following grammar and construct primitive NFAs and join
them together to form a
NFA that will recognize strings described by the regular expression. We will
do this step by step by
developing answers to the following questions. The production rules for this
language are given by
R . R*
R . R+
R . (R)
R . (R | R)
R . R.R
R . a
R . b
Question 1: Rewrite the grammar to remove left recursion.
Question 2: Identify the tokens of this language and write a scanner program
which can scan this
language and return tokens .
Question 3: Write a recursive descent parser which can parse this language
(based on the modified
grammar which removed left recursion) and yield a parse tree. Note that this
grammar has implicit
precedence. That is for a regular expression, a.b* the “*” operates on “b” and
not a.b as a whole. This
is true unless it is bracketed. In, (a.b)* on the other hand, the “*” operates on
(a.b) When you build a
parse tree you must take care of such precedences
Question 4: Now you need to write a program which can construct a NFAs
based on the parse tree
based on primitive NFAs. As discussed in class, primitive NFAs should be
joined together to form
NFA for the complete regular expression. This final NFA will be represented
as an adjacency matrix
described below. Thus the output of this program should be an adjacency
matrix.
Adjacency matrix: Any NFA is a directed graph. A directed graph G consists of
a set of nodes (in our
case states) and directed edges (in our case, transitions). For example, in the
graph below, A,B,C are
nodes and 1,2,3 are edges
A
B
C
1 2
3
Any directed graph can be represented by an adjacency matrix. For example,
the matrix below
represents the graph. Since edge “1” connects A to B, there is a “1” in the
row corresponding to “A”
and the column corresponding to “B”.
A B C
A 1 3
B 2
C
Similarly an NFA can be represented by an adjacency matrix. Note that more
than one element can be
present in a cell. For example, in the NFA if the edge from A to B is labeled
a,b then you would have
both “a” and “b” in the corresponding cell.
Question 5: Given such an adjacency matrix of an NFA and given an input
string consisting of a’s and
b’s write a program to simulate the NFA and output if the string is accepted
or rejected. Note : NFAs
can progress on multiple paths and you should simulate this effect – if one of
the paths results in accept
state then the input string is accepted by NFA.
Phase 2: To write a program which will construct a DFA from any NFA. You
will use adjacency
matrix as the representation and use epsilon closures to generate DFA.
Finally write a program to
simulate the DFA.
Bonus: Given an adjacency matrix for a DFA, write a program to produce
minimal DFA by state
merging.
File đính kèm:
 giao_trinh_mon_chuong_trinh_dich_phan_2.pdf
giao_trinh_mon_chuong_trinh_dich_phan_2.pdf

