Giáo trình Maple - Chương 5: Sử dụng Maple trong dạy và học toán
Phần mềm toán học và vai trò của người thầy
Một số người ít tiếp xúc với máy tính thường tưởng rằng máy tính vào nhà
trường sẽ làm cho học sinh lười học toán và làm cho các thầy dạy toán "mất
thiêng". Nếu quan niệm rằng "học toán là để làm bài tập, còn dạy toán là dạy cách
làm bài tập" thì đúng như vậy. Trên thực tế, máy tính sẽ làm cho các mẹo mực, tiểu
xảo giải bài tập trở thành "tầm thường". Trình độ toán học của mỗi người sẽ được
thể hiện (đánh giá) bằng khối lượng kiến thức cơ bản và khả năng xử lý các bài
toán thực tiễn (mà không qua mẹo mực làm bài tập, như lâu nay người ta vẫn lầm
tưởng). Điều này tất yếu đưa đến định hướng việc dạy và học vào những kiến thức
Toán học cơ bản và, theo định hướng này, vai trò người thầy sẽ được nâng cao lên
đúng tầm của mình: người thầy của sự nghiệp truyền bá “văn hoá toán học”, chứ
không phải là "thợ chữa bài tập".
Không ít người vẫn có ảo tưởng về những phần mềm có thể thay thế người thầy
trong giảng dạy toán học. Nhưng cho đến nay, với các khả năng tính toán và biểu
diễn tuyệt vời, phần mềm và máy tính vẫn chưa đáp ứng được kỳ vọng này. Ngoại
trừ một số chủ đề sơ đẳng được thể hiện bằng những phần mềm dạng "học mà chơi
- chơi mà học", việc giảng dạy những kiến thức cơ bản của Toán học vẫn đòi hỏi
công sức và tài năng sư phạm của người thầy, còn máy tính và phần mềm chỉ có thể
là công cụ đắc lực cho người thầy phát huy tài năng đó.
Ngày nay, trong nhà trường (kể cả các trường phổ thông ở nông thôn), máy
tính không còn là xa lạ, nhưng việc để cho máy tính điện tử (cùng các phần mềm)
thực sự trở thành công cụ cho việc giảng dạy của thầy và học tập của trò vẫn còn
gặp không ít khó khăn, vướng mắc. Có nhiều nguyên nhân dẫn đến tình trạng này,
nhưng lý do cơ bản là thiếu những phần mềm và phương pháp thiết thực phù hợp
với đối tượng và nội dung chương trình sách giáo khoa hiện hành ở nước ta. Khi
không còn ảo tưởng rằng phần mềm có thể làm nên tất cả, người ta sẽ thấy rằng
một trong những vấn đề cần phải đặt ra một cách nghiêm túc là: Không thể chỉ biết
sử dụng những gì có sẵn, mà còn phải biết gia công các chương trình hiện có,
hướng chúng vào việc phục vụ cho nội dung, phương pháp giảng dạy của mình, và
chỉ có như thế người thầy mới phát huy được các ưu thế sở trường của mình.
Như vậy, với phần mềm và máy tính, người giáo viên chẳng những không được
phép ỷ lại một cách thụ động vào những gì có sẵn, mà phải chủ động phát huy tối
đa khả năng sáng tạo của mình. Qua đó, vai trò của người thầy không hề bị máy
móc lấn lướt, mà được nâng lên tầm cao hơn: Người thầy của sự sáng tạo trong thời
đại công nghệ mới, mà không phải của sự nhồi nhét các loại tiểu xảo thông thường

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
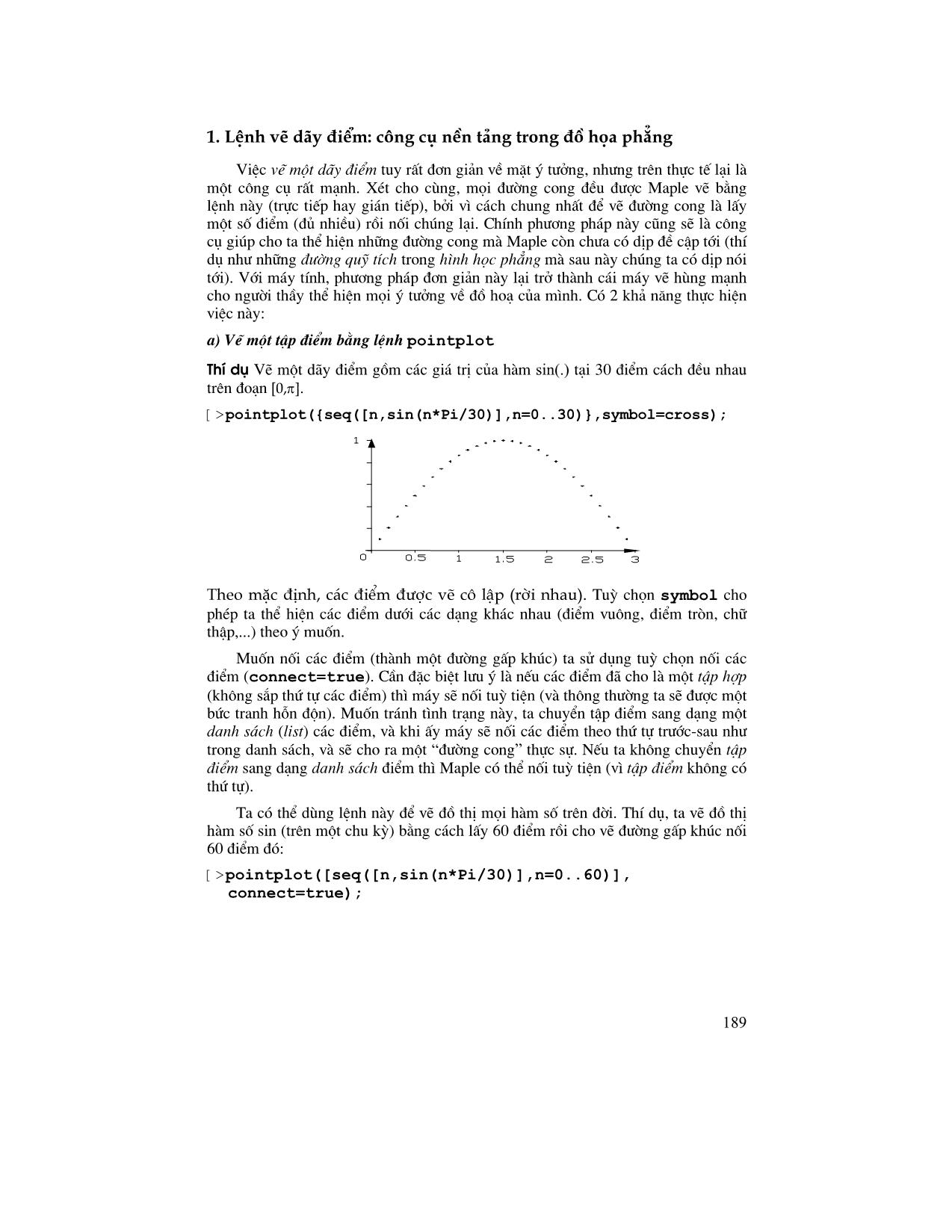
Trang 7
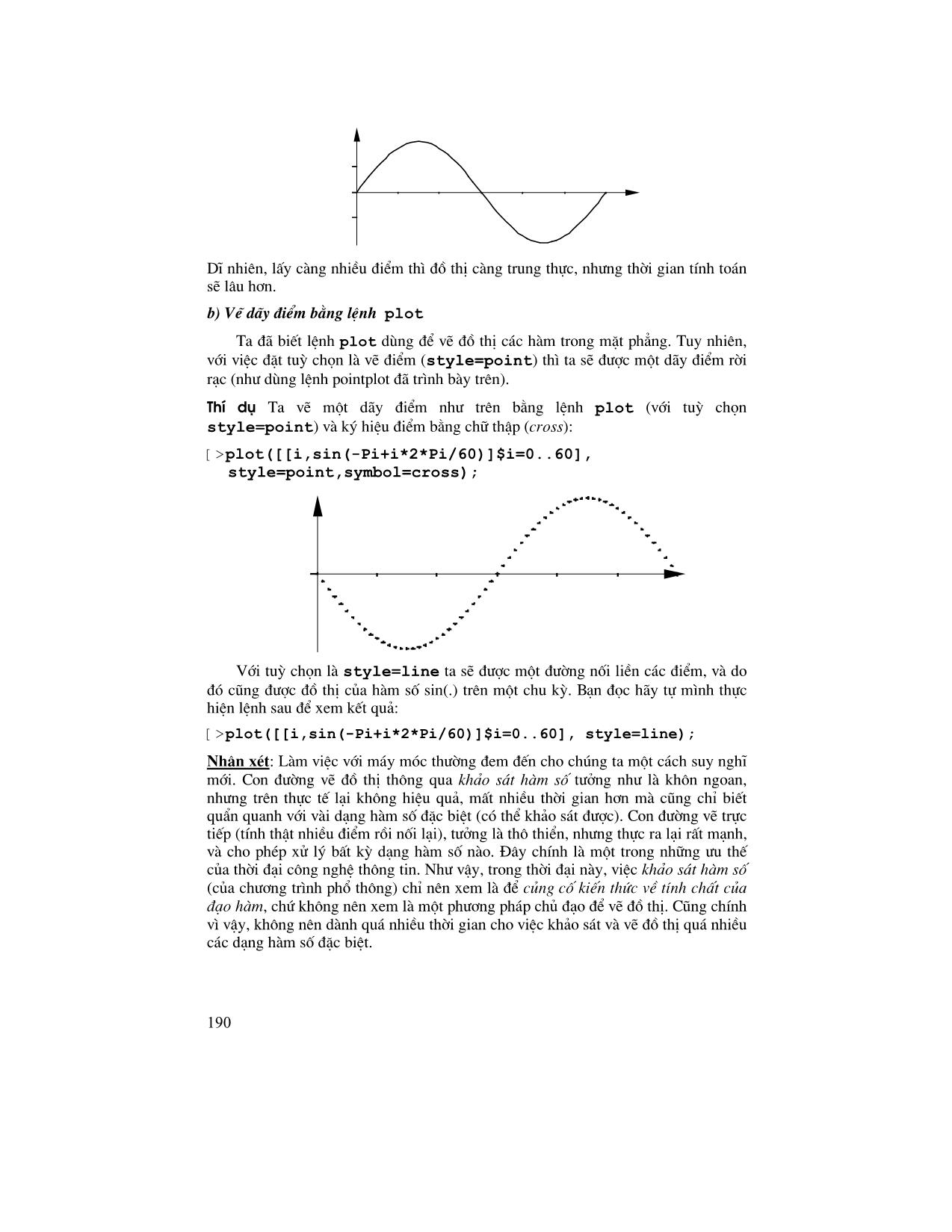
Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Giáo trình Maple - Chương 5: Sử dụng Maple trong dạy và học toán

xảo tìm nguyên hàm th−ờng là quá nhiều. Điều này khiến cho thầy đ−ợc "nhẹ gánh" về giảng giải, nh−ng lại làm cho học sinh bị "quá tải" vì làm bài tập (mà vẫn không nắm đ−ợc bản chất vấn đề). Máy tính hỗ trợ cho ta làm ng−ợc lại: ta không còn phải lo lắng nhiều về việc luyện kỹ xảo làm bài tập, mà có thể dành nhiều thời gian hơn cho việc giảng dạy bản chất vấn đề. Khi ấy, thầy sẽ phải mất nhiều thời gian và công sức hơn trong việc giảng giải, còn học sinh thì nhẹ nhàng hơn trong việc tiếp thu, và cũng không bị quá vất vả vì bài tập. Một ng−ời thầy có trách nhiệm thì luôn ý thức đ−ợc rằng cái "tải" không tự nhiên mất đi, và cách "giảm tải cho học sinh" hợp lý nhất là hãy để cho cái "tải" dồn sang phía thầy. Còn ng−ời thầy của thời đại công nghệ thông tin thì lại có thể dồn một phần "tải" sang cho máy tính. Đây chính là ph−ơng pháp "giảm tải cho học sinh" mà vẫn "bảo toàn", nếu không nói là "tăng c−ờng", về mặt chất l−ợng. Rõ ràng, trong rất nhiều chủ đề khác ta cũng gặp những tình huống t−ơng tự. Thí dụ: Nếu phần khảo sát và vẽ đồ thị hàm số chỉ dừng lại ở mục đích nắm đ−ợc các tính chất cơ bản của hàm khả vi thông qua đạo hàm của nó, và việc làm bài tập minh hoạ không quá đi sâu vào các tiểu xảo xử lý các dạng hàm số đặc biệt, thì ta rút gọn đ−ợc quá một nửa thời gian. T−ơng tự nh− vậy đối với phần giải ph−ơng trình và rất nhiều các phần khác, nếu đ−ợc xem xét lại một cách thấu đáo, chúng ta sẽ có đ−ợc ph−ơng án "giảm tải" khoa học và rất hiệu quả. Không thể phủ định vai trò quan trọng của việc rèn luyện t− duy thông qua giải các bài tập toán học, và cần dành thời gian xứng đáng cho công việc này. Tuy nhiên, cần phải tránh việc tập trung vào luyện các kỹ xảo làm bài tập một cách quá mức, đến nỗi không còn thời gian và công sức cho việc trau dồi các kiến thức cơ bản. Thật là nghịch lý nếu ta không dạy cho học sinh cách chứng minh những công thức, định lý rất cơ bản trong ch−ơng trình (công thức tính giới hạn của một tổng, công thức tính đạo hàm của các hàm l−ợng giác,...) vì sợ học sinh không tiếp thu nổi, mà lại mặc sức đ−a vào các loại bài tập với những chứng minh lắt léo và khó hiểu gấp nhiều lần. 5.3. Thiết lập những khả năng mới Nội dung phần này chỉ có ý nghĩa minh hoạ cho một h−ớng nghiên cứu với các chủ đề vô cùng phong phú, rộng mở cho tất cả những ai muốn phát huy sáng tạo trong việc dạy và học toán. Nó không đòi hỏi phải chuẩn bị nhiều, vì kiến thức khởi đầu chỉ cần nắm vững mấy ch−ơng đã trình bày trong tài liệu này. Với những ng−ời đã nắm đ−ợc các kiến thức đó, việc trình bày chi tiết về lập trình với các lệnh cụ thể sẽ là không cần thiết, mà điều cần quan tâm nhất là ý t−ởng. Chính vì vậy, những vấn đề trình bầy trong phần này chỉ mang tính gợi ý. Chủ đề đ−ợc chọn để minh hoạ trong phần này là vấn đề giảng dạy môn Hình học phẳng trong ch−ơng trình phổ thông. Phát triển cụ thể của các ý t−ởng nêu trong phần 210 này có thể tham khảo trong luận văn Thạc sỹ của tác giả Mai Công Mãn (xem danh mục tài liệu dẫn). Có thể khẳng định rằng, những gì Maple cung cấp trong gói Hình học, không đủ để đáp ứng cho nội dung giảng dạy ch−ơng trình môn hình học phẳng ở n−ớc ta. Tuy nhiên, chúng ta có thể nghiên cứu mở rộng gói công cụ hình học này để có thể thích ứng với đối t−ợng và phù hợp với ch−ơng trình sách giáo khoa hiện hành, qua đó có đ−ợc ph−ơng tiện giảng dạy tốt hơn cho bộ môn này. Thí dụ, trong Maple, ta chỉ có thể tìm thấy các lệnh để vẽ hình và tính toán trên các đối t−ợng hình học cơ bản nhất, mà không thể tìm đ−ợc các ph−ơng tiện thể hiện nội dung ch−ơng trình chúng ta đang dạy, chẳng hạn: Trong phần vẽ hình: Đối với đ−ờng thẳng chỉ mới có lệnh vẽ đ−ờng thẳng đi qua hai điểm có toạ độ cho sẵn, hay đã biết ph−ơng trình của nó, với tam giác mới có lệnh vẽ tam giác biết toạ độ ba đỉnh, với đ−ờng tròn cũng chỉ có các lệnh vẽ đ−ờng tròn đi qua ba điểm không thẳng hàng,v.v... Trong khi đó ch−ơng trình phổ thông lại đ−a ra rất nhiều cách xác định chúng (Ví dụ: Tam giác đ−ợc hoàn toàn xác định trong các tr−ờng hợp nh−: Biết ba đỉnh, biết cạnh-góc-cạnh, biết góc-cạnh- góc, biết cạnh-cạnh-cạnh...). Hơn nữa, trong thực tế ta gặp những tr−ờng hợp này nhiều hơn. Trong phần tính toán các đối t−ợng hình học: Maple chỉ mới nêu các lệnh nh−: Tính độ dài đoạn thẳng, tính diện tích tam giác, hình vuông, hình tròn, ellipse và một số hình đơn giản khác. Trong thực tế giảng dạy học tập cũng nh− trong đời sống, chúng ta lại hay phải tiếp xúc với những hình không đơn giản nh− vậy (Chẳng hạn: Hình tứ giác bất kỳ, hình thang, hình bình hành, hay phức tạp hơn là những hình đa giác bất kỳ...).Việc tính toán trên các đối t−ợng này mới thực sự là có ý nghĩa trong thực tiễn sản xuất và quản lý. Tóm lại, chúng ta cần nhấn mạnh một điều có tính then chốt là: Việc đ−a một công cụ tin học vào giảng dạy không cho phép ng−ời thầy thoả mãn với những gì có sẵn, mà luôn phải đào sâu suy nghĩ, phát huy tối đa năng lực sáng tạo. Chỉ có nh− vậy, phần mềm ứng dụng tin học nói chung và Maple nói riêng mới đ−ợc sử dụng rộng rãi trong hệ thống các ngành học, cấp học ở n−ớc ta. Sau đây là một số ví dụ về mở rộng khả năng của Maple. 5.3.1. Chủ đề đa giác trong hình học phẳng Đây là chủ đề khó đối với học sinh, vì trong ch−ơng trình hình học ở phổ thông đã không đ−ợc xét một cách hệ thống, mà chỉ có tính chất giới thiệu về nó. Nh−ng trong các bài tập thực hành có rất nhiều loại phải giải quyết trên đa giác. Đặc biệt trong đời sống hàng ngày, học sinh th−ờng xuyên tiếp xúc với các đồ vật mà hình ảnh của nó phần nhiều lại là những đa giác. Trong khi đó, qua thực tế giảng dạy chúng ta đều nhận thấy rằng kiến thức về đa giác của học sinh rất hạn chế do đó rất ngại khi tiếp xúc với loại toán này. Mặc dù Maple hầu nh− ch−a có sẵn các lệnh hỗ trợ cho giải quyết các bài toán trên đa giác nói chung, nh−ng nó cho phép chúng ta tạo các lệnh để vẽ và kiểm tra các tính chất của một đa giác. Bằng việc thiết lập các chu trình tính toán đơn giản, chúng ta dễ dàng thiết lập các lệnh mới, với các chức năng khá mạnh, trong đó có: 211 ♦ Kiểm tra tính lồi của một đa giác; ♦ Kiểm tra tính nội tiếp của một đa giác; ♦ Tính diện tích, tính chu vi của một đa giác bất kỳ (không tự cắt); Tức là, ta có thể làm cho học sinh thấy rằng, khi ra tr−ờng họ có thể làm việc trên mọi đối t−ợng hình học phức tạp mà không ngại. 5.3.2. Bài toán quỹ tích trong hình học phẳng Bài toán quỹ tích, một vấn đề mang nặng tính thách đố, luôn luôn gây e ngại cho bất kỳ ai, kể cả những học sinh rất giỏi, bởi lẽ ch−a có ai đ−a ra một ph−ơng pháp kiến thiết trong việc xử lý các bài toán loại này, mà chỉ dựa vào khả năng suy đoán, mẹo mực và kinh nghiệm. Với Maple, chúng ta có thể đ−a ra một ph−ơng pháp kiến thiết để giải các bài toán quỹ tích, khiến cho chúng mất tính huyền bí, kể cả đối với những học sinh bình th−ờng. Hơn thế, chúng ta có thể đề cập đến những loại quỹ tích đa dạng và phong phú hơn những gì đang xét trong ch−ơng trình phổ thông (cho đến nay), mà không gặp khó khăn gì hơn. Trong ch−ơng trình hình học phẳng, bài toán quỹ tích th−ờng đ−ợc trình bày d−ới nội dung là ''Tìm tập hợp tất cả các điểm M trên mặt phẳng thoả mãn một hay (một số) tính chất T nào đó''. Để giải quyết bài toán đặt ra, ng−ời ta th−ờng tiến hành theo các b−ớc sau 1. Phán đoán: Trong phần này, th−ờng ta lấy một số điểm ở các vị trí đặc biệt để phát hiện xem M nằm trên đ−ờng cong nào? 2. Phần thuận: Ta chứng tỏ điểm M có tính chất T thì thuộc hình (H). 3. Phần đảo: Ta chứng tỏ những điểm M thuộc hình (H) thì có tính chất T. 4. Giới hạn nếu có và kết luận: Tập hợp điểm M là hình (H). Lâu nay chúng ta vẫn ch−a đ−a ra một ph−ơng pháp kiến thiết để giải quyết bài toán này, nên việc giải nó chỉ thiên về kinh nghiệm. Tr−ớc một bài toán quỹ tích, việc giải đ−ợc nó đối với học sinh vẫn còn là sự may mắn và đa số cũng chỉ ở các bài toán cho dạng quỹ tích là đ−ờng thẳng hoặc đ−ờng tròn, chứ ở dạng quỹ tích khác thì rất hiếm. Nó luôn mang nặng tính thách đố đối với học sinh ở bậc học phổ thông, và th−ờng chỉ dành cho những học sinh khá giỏi. Điều này th−ờng làm cho học sinh thiếu tự tin, và dẫn đến hạn chế việc nâng cao kiến thức đối với học sinh. Với Maple chúng ta có thể đ−a ra một ph−ơng pháp kiến thiết để giải quyết các loại bài toán quỹ tích nói chung, nhằm giúp thầy giáo và học sinh v−ợt qua sự thách đố của nó. Với ph−ơng pháp này, bất cứ học sinh nào cũng có thể tiếp cận những bài toán quỹ tích một cách không ngần ngại. 1. Các loại quỹ tích thông th−ờng Vì trong ch−ơng trình hình học phẳng bậc phổ thông ta chỉ xét các dạng quỹ tích là đ−ờng thẳng hoặc đ−ờng tròn, cho nên ta gọi chúng là những dạng quỹ tích thông th−ờng. Bài toán đ−ợc giải quyết trên Maple nh− sau: 212 Tr−ớc hết ta lấy ba điểm phân biệt (nên xét những điểm này ở vị trí đặc biệt, dễ xác định nhất). Ta có thể kiểm tra xem chúng có thẳng hàng hay không bằng lệnh AreCoLinear . ắ Nếu chúng thẳng hàng ta vẽ đ−ờng thẳng qua ba điểm đó. Sau đó lấy điểm M bất kỳ (thoả mãn tính chất T ) và dùng lệnh IsOnLine để kiểm tra xem nó có thuộc đ−ờng thẳng này không. Nếu đúng ta kết luận quỹ tích các điểm cần tìm nằm trên đ−ờng thẳng đó. ắ Nếu chúng không thẳng hàng ta vẽ đ−ờng tròn qua ba điểm đó (bằng lệnh sẵn có trong Maple). Sau đó lấy một điểm M bất kỳ (thoả mãn tính chất T ) và dùng lệnh IsOnCircle kiểm tra xem điểm này có nằm trên đ−ờng tròn đó hay không (hoặc có thể dùng lệnh kiểm tra tứ giác nội tiếp, có thể thiết lập đ−ợc, để làm việc này). Nếu đúng ta kết luận quỹ tích các điểm cần tìm nằm trên đ−ờng tròn đó. Ph−ơng pháp này chỉ cho phép ta kết luận điểm M nằm trên đ−ờng thẳng hay đ−ờng tròn mà thôi (nh−ng đó cũng là vấn đề cốt yếu nhất mà ta cần). Để kết luận chính xác về quĩ tích của điểm M ta còn phải thêm phần giới hạn tập hợp điểm M . Để làm việc này ta có thể trở về ph−ơng pháp truyền thống nh− lâu nay. Nh− vậy nếu ta biết kết hợp ph−ơng pháp truyền thống với việc sử dụng công cụ Maple nh− trên, thì loại bài toán quĩ tích dạng thông th−ờng ta có thể giải quyết triệt để và đ−a ra kết luận qũi tích một cách chính xác. 2. Các loại quỹ tích khác Trong mục này ta xét các bài toán quỹ tích không phải là đ−ờng thẳng hay đ−ờng tròn, mà là một đ−ờng cong nào đó. Nói chung, loại quỹ tích này th−ờng không có công thức giải tích biểu diễn (nhất là trong phạm vi kiến thức ở phổ thông), hoặc nếu có thì chúng ta cũng ch−a có một ph−ơng pháp thể hiện đồ thị của các công thức này một cách chính xác tuyệt đối (L−u ý rằng, đồ thị của các hàm quen thuộc trong giáo trình phổ thông nh−: các hàm l−ợng giác, hàm mũ,... cũng không có cách biểu diễn chính xác tuyệt đối, mà chỉ đ−ợc vẽ một cách xấp xỉ với độ chính xác nào đó, bằng một tập điểm đủ dày). Nh− vậy, khi quỹ tích là một đ−ờng bất kỳ (không thẳng, không tròn), ta không hy vọng gì hơn là có đ−ợc biểu diễn xấp xỉ của nó với độ chính xác tuỳ ý, nh− có thể đạt đ−ợc với các đ−ờng cong quen biết trong giáo trình phổ thông. Rõ ràng bằng ph−ơng pháp thủ công chúng ta không thể làm đ−ợc điều này, nh−ng với Maple ta có thể đạt đ−ợc mong muốn ấy không mấy khó khăn. Muốn thực hiện điều này, ta chỉ cần sử dụng lệnh vẽ một dãy điểm (pointplot) kết hợp với tuỳ chọn (connect=true) để nối dãy điểm này lại. Ph−ơng pháp này tuy đơn giản (ai cũng hiểu đ−ợc) nh−ng rất cơ bản, và công cụ chính đề vẽ tất cả các loại đồ thị trên đời. L−u ý rằng, quỹ tích không thông th−ờng (không thẳng cũng không tròn) lại rất th−ờng xảy ra trong thực tiễn (xem các ví dụ đơn giản d−ới đây). Cho nên, Maple cho phép ta mở rộng đ−ợc phạm vi bài toán quỹ tích ra một miền rộng lớn hơn nhiều, mà không còn phải loanh quanh với 2 loại đ−ờng quỹ tích quen thuộc đã biết. Ví dụ 1 Cho đ−ờng tròn (O,r) nằm trong đ−ờng tròn (O', r'). Một tia Ot quay quanh O cắt hai đ−ờng tròn lần l−ợt tại A và B . Tìm quỹ tích các trung điểm của đoạn AB . 213 Bằng cách sinh một dãy cặp điểm đủ dày (t−ơng ứng trên các vòng tròn đã cho, nh− đầu bài qui định), ta dễ dàng tính đ−ợc dãy các trung điểm của các cặp điểm này. Cho máy vẽ dãy các trung điểm vừa tính đ−ợc ta có ngay quỹ tích cần tìm (nh− trong hình vẽ sau). Nhận xét: Một điều lý thú là, với hình vẽ trên, ta có cảm giác nh− quỹ tích là một đ−ờng tròn. Nếu chỉ bằng ph−ơng pháp thủ công nh− lâu nay, để kiểm tra xem điều đó đúng hay sai thì không đơn giản chút nào, ngay cả với những học sinh giỏi. Tuy nhiên với Maple, bằng cách chọn 4 điểm nào đó rồi dùng lệnh 'kiểm tra bốn điểm có nằm trên đ−ờng tròn không' thì ta có ngay kết luận rằng nó không phải là vòng tròn! Ví dụ 2 Cho đ−ờng tròn tâm O bán kính r và đ−ờng thẳng D cách tâm O một khoảng r<d . Ký hiệu N là điểm chạy trên đ−ờng thẳng D , và M là giao điểm của đ−ờng thẳng ON với đ−òng tròn . Tìm quỹ tích các trung điểm của đoạn MN . Với ph−ơng pháp hoàn toàn t−ơng tự nh− trên, ta có đ−ợc quỹ tích là đ−ờng cong trong hình vẽ sau: Nhận xét: Quỹ tích trên tuy rất đơn giản về mặt thiết lập, nh−ng nếu không có máy thì một học sinh giỏi cũng đành chịu bó tay. Với Maple, bài toán này không thể gọi là khó với ngay cả những học sinh bình th−ờng nhất! 5.4. Kết luận Các phân tích trên cho thấy rằng mẹo mực và kỹ xảo dù có tinh vi và phong phú đến đâu đi chăng nữa cũng không thể sánh đ−ợc với những ph−ơng pháp cơ bản, vốn đơn giản, dễ hiểu mà lại vô cùng vạn năng. Chính vì vậy, một biện pháp tốt và không tốn kém để tránh tụt hậu quá xa so với sự phát triển của thế giới là tránh tiêu phí thời gian và sức lực vào những việc không mang lại hiệu quả đáng kể. Chọn lọc tinh vi những gì cần thiết nhất, đồng thời nâng cao hiệu suất dạy và học thông qua việc tận 214 dụng các thành tựu công nghệ hiện đại là những điều cần làm ngay, nhất là trong ngành giáo dục đào tạo. Hành trang b−ớc vào thế kỷ 21 của thế hệ trẻ phải là: ph−ơng pháp cơ bản và công cụ mạnh. Muốn nắm đ−ợc ph−ơng pháp cơ bản phải học lý thuyết một cách nghiêm túc. Muốn có công cụ mạnh phải th−ờng xuyên cập nhật các thành tựu mới về khoa học và công nghệ. Việc sử dụng các phần mềm toán học hiện đại không những cho ta một công cụ tính toán hiệu quả, mà còn đem lại một cách học mới, đi sâu vào bản chất, đề cao các ph−ơng pháp cơ bản, tránh lãng phí quá nhiều thời gian cho các “tiểu xảo” trong Toán học. 215 Tài liệu dẫn 1. b.w.char., k.o. geddes, g.h. gonnet, b.l. leong, m.b. managan, s.m. watt, Maple V Library Reference Manual, Springer- Verlag, 1993; 2. phạm huy điển, tạ duy ph−ợng, đinh thế lục, H−ớng dẫn thực hành tính toán trên Maple, NXB Giáo dục, Hà Nội - 1998; 3. đinh thế lục, phạm huy điển, tạ duy ph−ợng, nguyễn xuân tấn, Giải tích Toán học: Những nguyên lý cơ bản và tính toán thực hành, NXB Giáo dục, Hà Nội - 1998; 4. Mai công mãn, Sử dụng Maple trong giảng dạy môn Hình học phẳng, Luận văn Thạc sỹ Toán học, Viện Toán học, 2000;
File đính kèm:
 giao_trinh_maple_chuong_5_su_dung_maple_trong_day_va_hoc_toa.pdf
giao_trinh_maple_chuong_5_su_dung_maple_trong_day_va_hoc_toa.pdf

