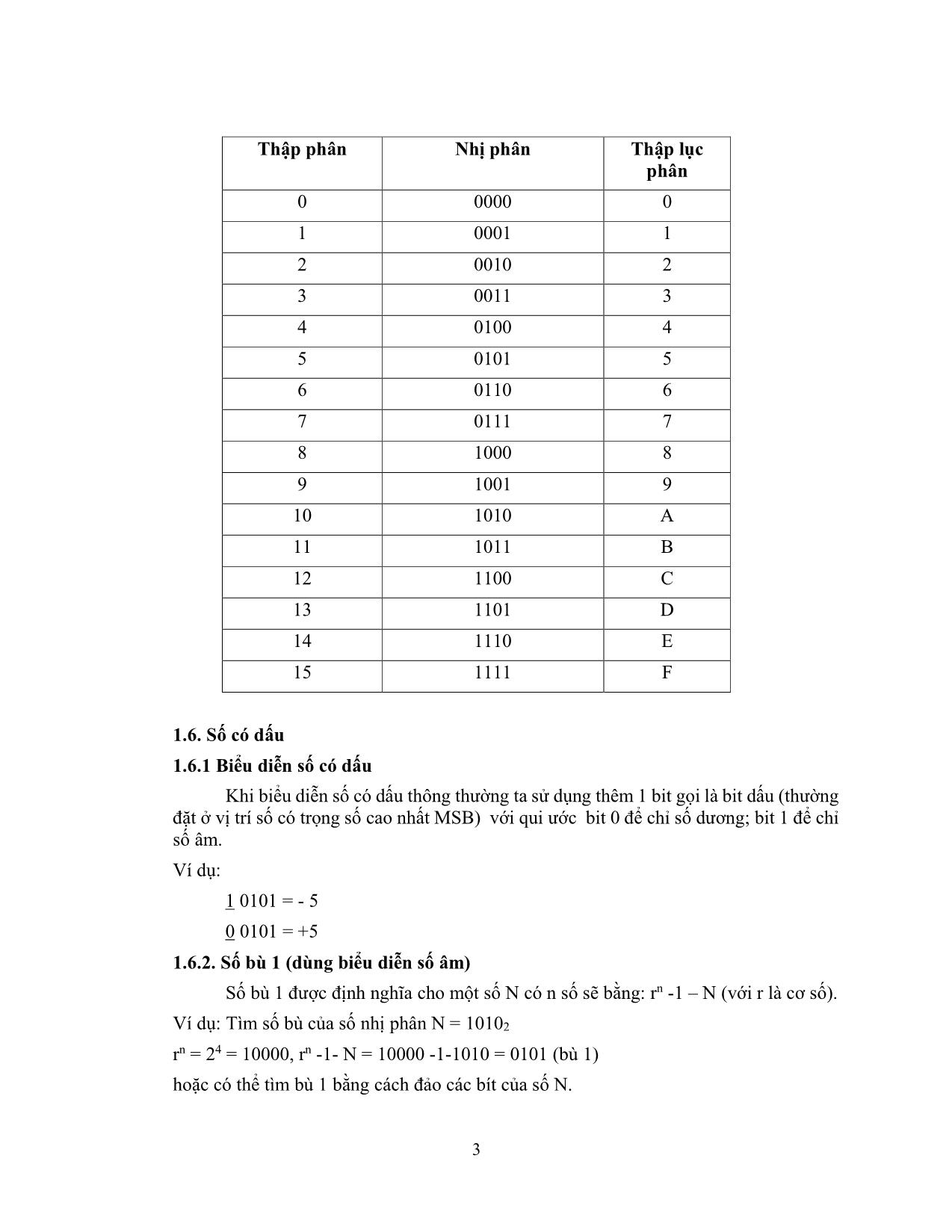
Giáo trình Điện tử số (Phần 1)

c nhấn (VÀ CÁC PHÍM P1P3 
KHÔNG NHẤN), nghĩa là khi P4 = 1 hoặc P5 = 1 hoặc P6 = 1 hoặc P7 = 1 
Vậy B = P4 + P5 + P6 + P7. 
C = 1 khi P2 hoặc P3 hoặc P6 hoặc P7 được nhấn, nghĩa là khi P2 = 1 hoặc P3 = 1 
hoặc P6 = 1 hoặc P7 = 1 
Vậy C = P2 + P3 + P6 + P7. 
D = 1 khi P1 hoặc P3 hoặc P5 hoặc P7 hoặc P9 được nhấn, nghĩa là khi P1 = 1 hoặc 
P3 = 1 hoặc P5 = 1 hoặc P7 = 1 hoặc P9 = 1 
Vậy D = P1 + P3 + P5 + P7 + P9. 
Mạch logic: 
3.3. Bộ giải mã 
 Bộ giải mã thực hiện chức năng ngược với bộ mã hóa. Cung cấp thông tin ở đầu 
ra khi đầu vào xuất hiện tổ hợp các biến nhị phân ứng với 1 hay nhiều từ mã đã được 
chọn. 
Từ từ mã xác định được tín hiệu tương ứng với đối tượng đã mã hóa. 
D 
C 
B 
A 
P1 
P2 
P3 
P4 
P5 
P6 
P7 
P8 
P9 
28 
Có 2 trường hợp giải mã: 
- Giải mã cho 1 từ mã (cấu hình) 
Nguyên lý: ứng với một tổ hợp cần giải mã ở đầu vào thì đầu ra bằng 1, các tổ 
hợp đầu vào còn lại, đầu ra bằng 0. 
 Sơ đồ khối: 
- Giải mã cho toàn bộ mã: 
Nguyên lý: ứng với một tổ hợp nào đó ở đầu vào thì 1 trong các đầu ra bằng 1, 
các đầu ra còn lại bằng 0. 
Ví dụ: với bộ giải mã cho toàn bộ từ mã có 2 đầu vào và 4 đầu ra như sau, thì với 
AB=00, đầu ra S0 = 1, còn S1, S2, S3 = 0. Tương tự với các giá trị AB còn lại. 
Sơ đồ khối: 
3.3.1. Bộ giải mã BCD (Binary Coding Decimal) 
Mã BCD là mã dùng hệ nhị phân để mã hóa cho hệ thập phân ( các chữ số từ 0 đến 9). 
BGM 
Từ mã 
Tín hiệu 
xác định 
đối tượng 
A 
B 
S 
BG
M 
S0 
S1 
S2 
S3 
A 
B 
B
G
M 
29 
Bảng mã: 
Xác định đầu vào, đầu ra cho bộ giải mã BCD 
Vào: từ mã nhị phân 4 bit 
Ra: các tín hiệu tương ứng với các số nhị phân mà từ mã mã hóa 
Do có 4 bit, nên có 16 tổ hợp. Ta chỉ sử dụng 10 tổ hợp, còn 6 tổ hợp không sử 
dụng đến, ta coi là không xác định. Nhờ đó ta có thể tối thiểu hóa các biểu thức của đầu 
ra. 
Sơ đồ khối bộ giải mã BCD: 
Chữ số thập 
phân 
0 
1 
2 
3 
4 
5 
6 
7 
8 
9 
Từ mã nhị phân 
0000 
0001 
0010 
0011 
0100 
0101 
0110 
0111 
1000 
1001 
S0 
S1 
S9 
Bộ GM 
BCD 
A 
B 
C 
D 
30 
Bảng sự thật: 
ABCD S0 S1 S2 S3 S4 S5 S6 S7 S8 S9 
0000 1 0 0 0 0 0 0 0 0 0 
0001 0 1 0 0 0 0 0 0 0 0 
0010 0 0 1 0 0 0 0 0 0 0 
0011 0 0 0 1 0 0 0 0 0 0 
0100 0 0 0 0 1 0 0 0 0 0 
0101 0 0 0 0 0 1 0 0 0 0 
0110 0 0 0 0 0 0 1 0 0 0 
0111 0 0 0 0 0 0 0 1 0 0 
1000 0 0 0 0 0 0 0 0 1 0 
1001 0 0 0 0 0 0 0 0 0 1 
1010 x x x x x x x x x x 
1011 x x x x x x x x x x 
1100 x x x x x x x x x x 
1101 x x x x x x x x x x 
1110 x x x x x x x x x x 
1111 x x x x x x x x x x 
Tìm biểu thức của từng đầu ra phụ thuộc vào đầu vào 
S0(A,B,C,D)= A B C D 
 CD 
AB 00 01 11 10 
00 
1 
0 0 0 
01 0 0 0 0 
11 x x x x 
10 0 0 x x 
S1(A,B,C,D)= A B C D 
 CD 
AB 00 01 11 10 
00 0 1 0 0 
01 0 0 0 0 
11 x x x x 
10 0 0 x x 
31 
S2(A,B,C,D)= B C D 
 CD 
AB 
00 01 11 
10 
00 0 0 0 1 
01 0 0 0 0 
11 X X X X 
10 0 0 X X 
S3= B CD 
 CD 
AB 00 01 11 10 
00 0 0 1 0 
01 0 0 0 0 
11 X X X X 
10 0 0 
X 
X 
S4=B C D 
 CD 
AB 00 01 11 10 
00 0 0 0 0 
01 
1 
0 0 0 
11 X X X X 
10 0 0 X X 
S5=B C D 
 CD 
AB 00 01 11 10 
00 0 0 0 0 
01 0 
1 
0 0 
11 X X X X 
10 0 0 X X 
32 
S6=BC D 
 CD 
AB 00 01 11 10 
00 0 0 0 0 
01 0 0 0 1 
11 X X X X 
10 0 0 X X 
S7=BCD 
 CD 
AB 00 01 11 10 
00 0 0 0 0 
01 0 
0 
1 0 
11 - - - - 
10 0 0 - - 
S8=A D 
 CD 
AB 00 01 11 10 
00 0 0 0 0 
01 0 0 0 0 
11 
X X X X 
10 1 0 X X 
 S9=AD 
 CD 
AB 00 01 11 10 
00 0 0 0 0 
01 0 0 0 0 
11 X 
X 
X X 
10 0 1 X X 
33 
Mạch logic: 
3.3.2. Bộ giải mã địa chỉ 
Mỗi bộ vi xử lý có khả năng quản lý một không gian nhớ nhất định. Không gian 
nhớ được chia thành các ngăn nhớ và mỗi ngăn nhớ có một địa chỉ xác định, duy nhất. 
Bộ vi xử lý muốn làm việc (đọc, ghi) với ngăn nhớ nào thì phải phát ra địa chỉ của ngăn 
nhớ đó. 
Giải mã địa chỉ bộ nhớ: 
- Đầu vào: tín hiệu địa chỉ ngăn nhớ phát ra từ bộ vi xử lý 
- Đầu ra: xác định ngăn nhớ nào 
 Ngoài ra còn đầu vào CS (Chip Select) để lựa chọn chip nhớ làm việc. 
Nếu CS=0 thì không được vào lấy địa chỉ 
Nếu CS=1 thì được lấy địa chỉ 
Chức năng: từ tín hiệu địa chỉ phát ra từ bộ vi xử lý, xác định ngăn nhớ nào sẽ 
trao đổi dữ liệu với bộ vi xử lý. 
Sơ đồ khối mạch giải mã địa chỉ: 
S0 
S1 
S2n-1 
BGM 
địa 
chỉ 
Phát 
địa 
chỉ 
0 1 1 0 1 0 0 1 
1 0 1 0 1 0 1 1 
0 1 1 0 1 0 1 0 
n 
CS 
34 
- Bộ giải mã 2-4: 
Sơ đồ khối bộ giải mã 2- 4: 
Bảng sự thật: 
E1 E0 S0 S1 S2 S3 
0 0 1 0 0 0 
0 1 0 1 0 0 
1 0 0 0 1 0 
1 1 0 0 0 1 
Từ bảng sự thật ta có: 
S0 =   ; S1 =  E0 ; S2 = E1 ; S3 = E1E0 
Sơ đồ mạch logic: 
Ta thêm tín hiệu CS (Enable) vào bộ giải mã để lựa chọn bộ giải mã hoạt động hay 
không. 
CS=0, hệ không hoạt động, tất cả các đầu ra =0 
CS=1, hệ hoạt động bình thường 
BGM 
2-4 
E1 
E0 
S0 
S1 
S2 
S3 
CS 
BGM 
2-4 
E1 
E0 
S0 
S1 
S2 
S3 
E0 
E1 
S0 
S1 
S2 
S3 
35 
Sơ đồ logic: 
- Bộ giải mã 3-8: 
Sơ đồ khối: 
Bảng sự thật: 
E2 E1 E0 S0 S1 S2 S3 S4 S5 S6 S7 
0 0 0 1 0 0 0 0 0 0 0 
0 0 1 0 1 0 0 0 0 0 0 
0 1 0 0 0 1 0 0 0 0 0 
0 1 1 0 0 0 1 0 0 0 0 
1 0 0 0 0 0 0 1 0 0 0 
1 0 1 0 0 0 0 0 1 0 0 
1 1 0 0 0 0 0 0 0 1 0 
1 1 1 0 0 0 0 0 0 0 1 
Nhận xét: 
Khi E2 = 0 
S 0 S3 phụ thuộc vào (E1, E0) như một Bộ giải mã 2-4 
S4 S7 = 0 
Khi E2 = 1 
S0 
S7 
BGM 
3-8 
E2 
E1 
E0 
S0 
S1 
S2 
S3 
E0 E1 
36 
S0 S3 = 0 
S4 S7 phụ thuộc vào (E1,E0) như một Bộ giải mã 2-4 
Ta có thể sử dụng 2 bộ giải mã 2 đầu vào để lắp thành 1 bộ giải mã 3-8. 
3.4. Bộ chuyển đổi mã BCD sang mã 7 đoạn 
Dùng để chuyển từ mã BCD sang mã hiển thị 7 thanh, mỗi thanh là một điốt phát quang. 
Sơ đồ khối bộ chuyển đổi mã BCD -7 đoạn: 
a b c d e f g 
b 
c 
d 
e 
a 
f 
g 
E0 
S0 
S1 
S2 
S3 
S4 
S5 
S6 
S7 
E1 
2-4 
CS 
E2 
CS 
2-4 
A 
B 
C 
a 
b 
c 
d 
e 
D f 
g 
37 
Bảng sự thật: 
A B C D a b c d e f g 
0 0 0 0 1 1 1 1 1 1 0 
0 0 0 1 0 1 1 0 0 0 0 
0 0 1 0 1 1 0 1 1 0 1 
0 0 1 1 1 1 1 1 0 0 1 
0 1 0 0 0 1 1 0 0 1 1 
0 1 0 1 1 0 1 1 0 1 1 
0 1 1 0 1 0 1 1 1 1 1 
0 1 1 1 1 1 1 0 0 0 0 
1 0 0 0 1 1 1 1 1 1 1 
1 0 0 1 1 1 1 1 0 1 1 
1 0 1 0 - - - - - - - 
1 0 1 1 - - - - - - - 
1 1 0 0 - - - - - - - 
1 1 0 1 - - - - - - - 
1 1 1 0 - - - - - - - 
1 1 1 1 - - - - - - - 
Biểu diễn đầu ra phụ thuộc vào các đầu vào: 
a = A + C + B D + BD 
 CD 
AB 
00 
01 11 10 
00 1 0 1 1 
01 0 1 1 1 
11 - - - - 
10 1 1 - - 
b = B + C D + CD 
 CD 
AB 00 01 11 10 
00 
1 
1 1 1 
01 1 0 1 0 
11 - - - - 
10 1 1 - - 
38 
c = D + C + B 
 CD 
AB 00 01 11 10 
00 1 1 1 0 
01 1 1 1 1 
11 - - - - 
10 1 1 - - 
d = A + C D + B C + B D + B C D 
 CD 
AB 00 01 11 10 
00 1 0 1 1 
01 0 1 0 1 
11 - - - - 
10 1 1 - - 
e = B D + C D 
 CD 
AB 00 01 11 10 
00 1 0 0 1 
01 0 0 0 1 
11 - - - - 
10 1 0 - - 
f = C D + B C + B D 
 CD 
AB 00 01 11 10 
00 
1 0 0 0 
01 1 1 0 1 
11 - - - - 
10 1 0 - - 
39 
g = A + B C + C D + B C 
 CD 
AB 
00 
01 11 10 
00 0 0 1 1 
01 1 1 0 1 
11 - - - - 
10 1 1 - - 
Sơ đồ mạch bộ giải mã 7 đoạn: 
40 
3.5. Bộ dồn kênh và bộ phân kênh (Multiplexer/DeMultiplexer–MUX/DEMUX) 
3.5.1. Bộ dồn kênh (MUX) 
Mạch dồn kênh hay còn gọi là MUX là mạch có 2n dữ liệu (Data), n ngõ vào điều 
khiển (Selects) và có một ngõ ra 
Chức năng: chọn 1 tín hiệu trong nhiều tín hiệu đầu vào để đưa ra đầu ra 
Mạch MUX 2-1: 
Sơ đồ khối: 
Tín hiệu chọn: 
C0 S 
0 E0 
1 E1 
Tín hiệu ra S = 0C E0 + C0E1 
Mạch MUX 4-1: 
Sơ đồ khối: 
Tín hiệu chọn: 
C1 C0 S 
0 0 E0 
0 1 E1 
1 0 E2 
1 1 E3 
Tín hiệu ra S = 1C 0C E0 + 1C C0E1 + C1 0C E2 + C1C0E3. 
E3 
E2 
E1 
E0 
C1 
C0 
S 
C0 
E1 
E0 
S 
41 
- Thiết kế MUX 2-1 
Bảng sự thật: 
C0 E1 E0 S 
0 0 0 0 
0 0 1 1 
0 1 0 0 
0 1 1 1 
1 0 0 0 
1 0 1 0 
1 1 0 1 
1 1 1 1 
Biểu thức đầu ra S: S = 0C E0 + C0E1 
 E1E0 
C0 
00 01 11 10 
0 0 1 1 0 
1 0 0 1 1 
Sơ đồ mạch: 
 Ứng dụng của Bộ chọn kênh 
a. Chọn nguồn tin 
Giả thiết có 2 nguồn tin A, B, mỗi nguồn 4 bit 
A: a3a2a1a0 
B: b3b2b1b0 
Sơ đồ mạch bộ chọn 2 nguồn tin A và B: 
E0 
E1 
C0 
& 
& 
S 
C0 
a3 a2 a1 a0 b3 b2 b1 b0 
S3 S2 S1 S0 
42 
Khi C0 = 0 
Mux 3 : S3 = a3 
Mux 2 : S2 = a2 
Mux 1 : S1 = a1 
Mux 0 : S0 = a0 
Vậy S = A 
Khi C0 = 1 
Mux 3 : S3 = b3 
Mux 2 : S2 = b2 
Mux 1 : S1 = b1 
Mux 0 : S0 = b0 
Vậy S = B 
b. Bộ chuyển đổi song song – nối tiếp 
Bộ chuyển đổi kênh thực hiện việc chuyển đổi từ truyền song song sang truyền 
nối tiếp 
c.Tạo hàm logic 
MUX có thể được sử dụng để tạo hàm logic 
Ví dụ: MUX 4-1: 
S = 1C 0C E0 + 1C C0E1 + C1 0C E2 + C1C0E3. 
Mặt khác áp dụng định lý Shannon để khai triển hàm 2 biến bất kỳ ta có: 
F(a,b) = a b f(0,0) + abf(0,1) + ab f(1,0) + abf (1,1) 
E3 
E2 
E1 
E0 
C1 
C0 
S 
 S0 
 E0 E1 E2 E3 t 
 t0 t1 t2 t3 
 C1 
 t
 C0 
 t
E3 
E2 
E1 
E0 
C1 
C0 
S 
43 
So sánh ta thấy sự tương ứng 1-1 giữa: 
S và F(a, b); C1 và a; C0 và b; E0 và f(0, 0) 
E1 và f(0, 1) 
E2 và f(1, 0) 
E3 và f(1, 1) 
Vậy ta có cách tạo hàm 2 biến bất kỳ bằng cách sử dụng bộ chọn kênh 4-1 với sự 
tương ứng như trên. 
Ví dụ: Tạo hàm F(A, B) = A + B 
Bảng sự thật: 
A B F 
0 0 0 
0 1 1 
1 0 1 
1 1 1 
Mạch tạo hàm F = A+B bằng MUX 4-1: 
Ví dụ: Tạo hàm F(A, B) = AB 
Bảng thật: 
A B F 
0 0 0 
0 1 0 
1 0 0 
1 1 1 
Mạch tạo hàm F= A.B bằng MUX 4-1: 
E3 = 1 
E2 = 1 
E1 = 1 
E0 = 0 
A 
B 
S F 
44 
3.5.2. Bộ phân kênh (Demultiplexer – DeMUX) 
DEMUX là mạch tổ hợp có 1 ngõ vào, n ngõ điều khiển và 2n ngõ ra.Nếu dữ liệu 
từ MUX đưa đến DEMUX thì dữ liệu sẽ được phục hồi đúng trạng thái ban đầu. 
Chức năng: đưa tín hiệu từ đầu vào tới 1 trong những đầu ra. 
- Mạch DeMUX 1-2 
Sơ đồ khối: 
Tín hiệu chọn: 
C0 S0 S1 
0 E 0 
1 0 E 
- Mạch DeMUX 1-4 
Sơ đồ khối: 
E 
 S0 
S1 
S F 
E3 = 1 
E2 = 0 
E1 = 0 
E0 = 0 
A 
B 
E 
C1 
C0 
S0 
S1 
S2 
S3 
45 
Tín hiệu chọn: 
C1 C0 S0 S1 S2 S3 
0 0 E 0 0 0 
0 1 0 E 0 0 
1 0 0 0 E 0 
1 1 0 0 0 E 
Các ngõ ra: 
S0 =  E 
S1 = C0E 
S2 = C1E 
S3 = C0C1E 
Sơ đồ logic mạch DEMUX 1:4: 
C0 
C1 
S0 
S1 
S2 
S3 
E 
46 
3.6. Các mạch số học 
3.6.1. Bộ cộng 
a.Bộ cộng bán phần (Half-Adder) 
 Bộ cộng bán phần là hệ tổ hợp có nhiệm vụ thực hiện phép cộng số học là 2 bit nhị 
phân ngõ vào ai và bi; hệ có 2 ngõ ra: bit tổng Si (Sum) và bit nhớ Ci+1 (Carry). 
Sơ đồ khối: 
Bảng sự thật: 
ai bi Si Ci+1 
0 0 0 0 
0 1 1 0 
1 0 1 0 
1 1 0 1 
Biểu thức đầu ra phụ thuộc đầu vào: 
Ci+1 = ai.bi 
Si = ai  bi 
Sơ đồ mạch logic: 
b.Bộ cộng đầy đủ (Full-Adder) 
Thực hiện phép cộng giữa 2 bit bất kỳ của phép cộng 2 số nhị phân ( có số nhớ 
trước). 
Sơ đồ khối: 
 C i: số nhớ đầu vào. 
Ci+1: số nhớ đầu ra. 
ai Ci+1 
bi Si 
& 
=1 
ai Si 
bi Ci+1 
HA 
47 
Bảng sự thật: 
ai bi Ci Si Ci+1 
0 0 0 0 0 
0 0 1 1 0 
0 1 0 1 0 
0 1 1 0 1 
1 0 0 1 0 
1 0 1 0 1 
1 1 0 0 1 
1 1 1 1 1 
Biểu thức đầu ra phụ thuộc đầu vào: 
Si = ai  bi  Ci 
Ci+1= ai.bi + Ci(ai bi) 
 aibi 
Ci 
00 01 11 10 
0 0 0 1 0 
1 0 1 1 1 
Sơ đồ mạch logic: 
=1 =1 
& 
& 
>=1 
ai 
bi 
Ci 
si 
Ci+1 
FA 
ai 
bi 
Ci 
Si 
Ci+1 
48 
c. Bộ cộng song song 
Đây là bộ cộng 2 số nhị phân n bit, kết quả nhận được là 1 số nguyên n+1 bit. 
A an-1 an-2 ....... a1 a0 
B bn-1 bn-2 ....... b1 b0 
S sn sn-1 sn-2 ....... s1 s0 
Sơ đồ mach logic: 
3.6.2. Bộ trừ 
a. Bộ trừ bán phần (Half-Substractor) 
Dùng để thực hiện phép trừ giữa 2 bit nhị phân ai và bi; ngõ ra là hiệu Di và số 
nhớ âm (mượn) Bi+1. 
Sơ đồ khối: 
Bảng sự thật: 
ai bi Di Bi+1 
0 0 0 0 
0 1 1 1 
1 0 1 0 
1 1 0 0 
Biểu thức đầu ra phụ thuộc đầu vào 
Di= ai bi 
Bi+1= ia bi 
Sơ đồ logic: 
FAn-2 FAn-1
FA0 FA1
. 
an-1bn-1 an-2bn-2 a1b1 a0b0 
Cn-1 Cn-2 C1 C0 = 0 
C1 C2 Cn-1 Cn 
sn-1 sn-2 s1 s0 sn 
ai Di 
bi Bi+1 
HS 
49 
b.Bộ trừ đầy đủ (Full-Substractor) 
Dùng để thực hiện trừ giữa 2 bit bất kỳ trong phép trừ 2 số nhị phân 
Sơ đồ khối: 
Bảng sự thật: 
Bi ai bi Bi+1 Di 
0 0 0 0 0 
0 0 1 1 1 
0 1 0 0 1 
0 1 1 0 0 
1 0 0 1 0 
1 0 1 1 0 
1 1 0 0 1 
1 1 1 1 1 
Biểu thức đầu ra phụ thuộc đầu vào 
Di = ai  bi  Bi 
Bi+1= ia bi + Bi ( ii ba  ) 
Mạch logic: 
 ai Di 
bi 
 Bi+1 
=1 
& 
ai Bi+1 
bi 
Bi Di 
FS 
50 
3.7. Bộ so sánh 
Có 2 loại mạch so sánh 2 số nhị phân: 
- So sánh đơn giản: kết quả so sánh: bằng nhau, khác nhau 
- So sánh đầy đủ: kết quả so sánh: lớn hơn, nhỏ hơn, bằng nhau 
3.7.1. Bộ so sánh đơn giản 
Xây dựng bộ so sánh đơn giản 2 số A và B: 
A a3 a2 a1 a0 
B b3 b2 b1 b0 
Đầu ra S: 
S = 1 A = B 
S = 0 A B 
Ta có: 
 
 
 
 

 
 
 
 

 
1
1
1
1
0
0
0
0
00
11
22
33
00
11
22
33
00
11
22
33
ba
ba
ba
ba
ba
ba
ba
ba
ba
ba
ba
ba
BA 
Vậy 00112233 ... babababaS  
Sơ đồ mạch logic: 
=1 =1 
& 
& 
>=1 
ai 
bi 
Bi 
Di 
Bi+1 
Bộ so 
sánh 
đơn 
giản 
A 4 
B 4 
S 
51 
3.7.2. Bộ so sánh đầy đủ 
a. Bộ so sánh đầy đủ 2 bit 
Đầu vào: 2 bit cần so sánh ai và bi. 
Đầu ra: 3 tín hiệu để báo kết quả lớn hơn, nhỏ hơn, bằng nhau của 2 bit 
ai > bi Gi = 1 còn Ei, Li = 0 
ai Li = 1 còn Ei, Gi = 0 
ai = bi Ei = 1 còn Gi, Li = 0 
Sơ đồ khối: 
Bảng sự thật: 
ai bi Gi Li Ei 
0 0 0 0 1 
1 0 1 0 0 
0 1 0 1 0 
1 1 0 0 1 
Biểu diễn đầu ra theo đầu vào: 
Gi = ii ba 
Li = iiba 
Ei = ii ba  . 
Sơ đồ mạch logic: 
=1 
a3 
b3 
=1 
a2 
b2 
=1 
a1 
b1 
=1 
a0 
b0 
& 
S 
Bộ so 
sánh 
đầy đủ 
ai 
bi 
Li 
Gi 
Ei 
52 
c. Bộ so sánh đầy đủ 2 số nhị phân nhiều bit 
Có cấu tạo gồm các bộ so sánh 2 bit 
Có tín hiệu CS: 
- CS = 0, tất cả các đầu ra = 0 
- CS = 1, hoạt động bình thường. 
Khi đó, các đầu ra của bộ so sánh 2 bit có biểu thức: 
Gi = CS ii ba 
Li = CS iiba 
Ei = CS( ii ba  ). 
Sơ đồ mạch bộ so sánh 2 số 3 bit: 
A: a2 a1 a0 
B: b2 b1 b0 
ai bi Gi 
 Li 
 Ei 
& 
& 
=1 
Bộ so 
sánh 
đầy đủ 
a1 
b1 
L1 
G1 
E1 
Bộ so 
sánh 
đầy đủ 
a2 
b2 
L2 
G2 
E2 
Bộ so 
sánh 
đầy đủ 
a0 
b0 
L0 
G0 
E0 
CS 
CS 
 1 
 1 
G 
L 
E 
53 
Bài tập chương 3 
1. Một mạch tổ hợp có 5 ngõ vào A, B, C, D, E và một ngõ ra Y. Ngõ vào là một từ mã 
thuộc bộ mã như sau 
E D C B A 
0 0 0 0 0 
0 0 1 1 1 
0 1 0 0 0 
0 1 1 1 1 
1 0 0 0 0 
1 0 1 1 1 
1 1 0 0 0 
1 1 1 1 1 
a. Thiết kế mạch tổ hợp dùng cổng AND-OR sao cho Y=1 khi ngõ vào là một từ 
mã đúng và Y=0 khi ngõ vào là một từ mã sai. 
b. Thực hiện lại câu a chỉ dùng toàn cổng NAND 
2. Cho một hệ tổ hợp hoạt động theo bảng sau 
E X1 X0 Y0 Y1 Y2 Y3 
1 X X 1 1 1 1 
0 0 0 0 1 1 1 
0 0 1 1 0 1 1 
0 1 0 1 1 0 1 
0 1 1 1 1 1 0 
 Thiết kế hệ tổ hợp này dùng toàn cổng NOT và NAND 3 ngõ vào 
3. Thiết kế mạch trừ hai số một bit, trong đó V là biến điều khiển, Ci-1 là số mượn ngõ 
vào, Ci là số mượn ngõ ra. Khi V=0 thì mạch thực hiện D=A-B, khi V=1 thì thực hiện 
D=B-A 
4. Thiết kế mạch trừ hai số 3 bit A và B với biến điều khiển V, dựa trên cơ sở mạch trừ 
hai số một bit ở bài trên.