Giải thuật Chaotic Vortex Search cho bài toán tối ưu toàn cục

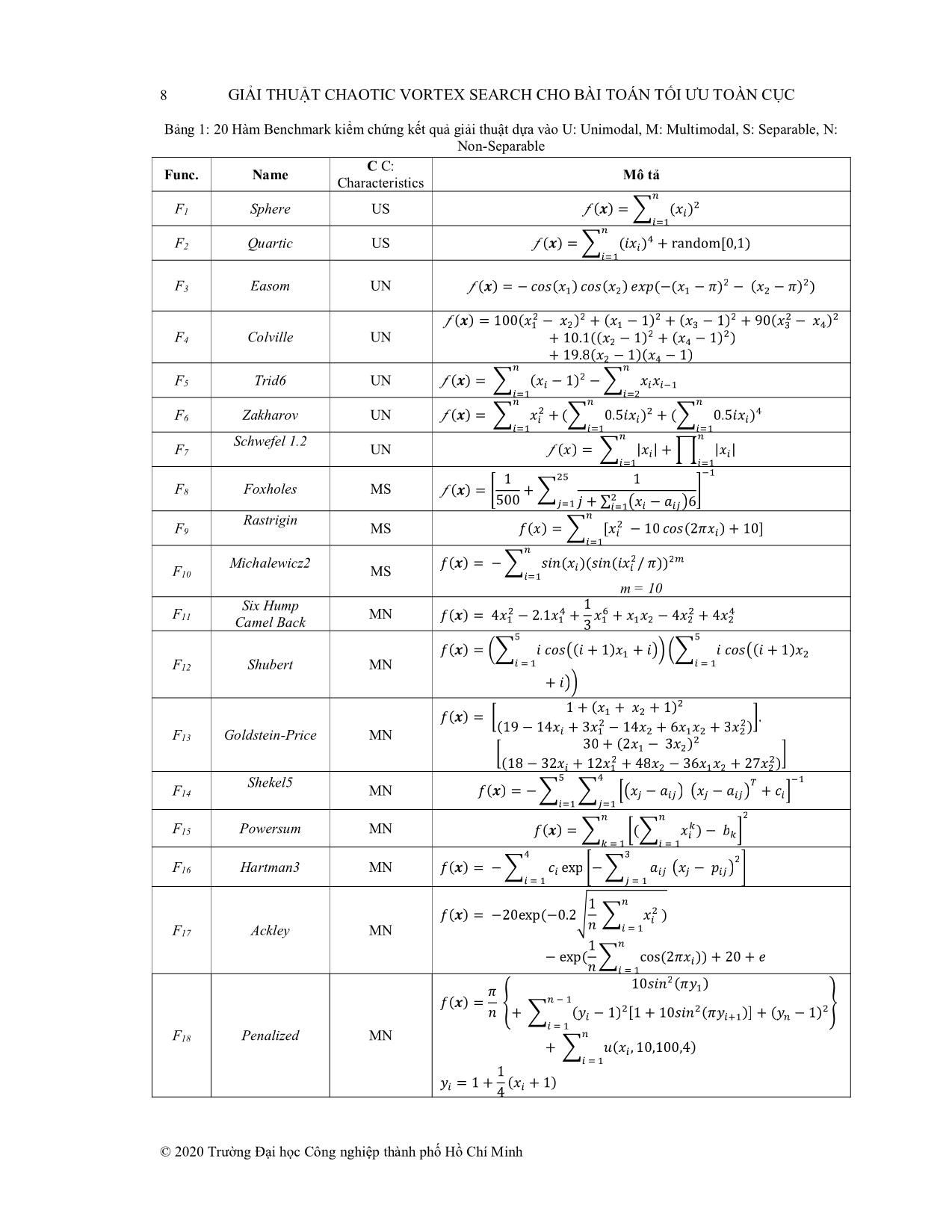
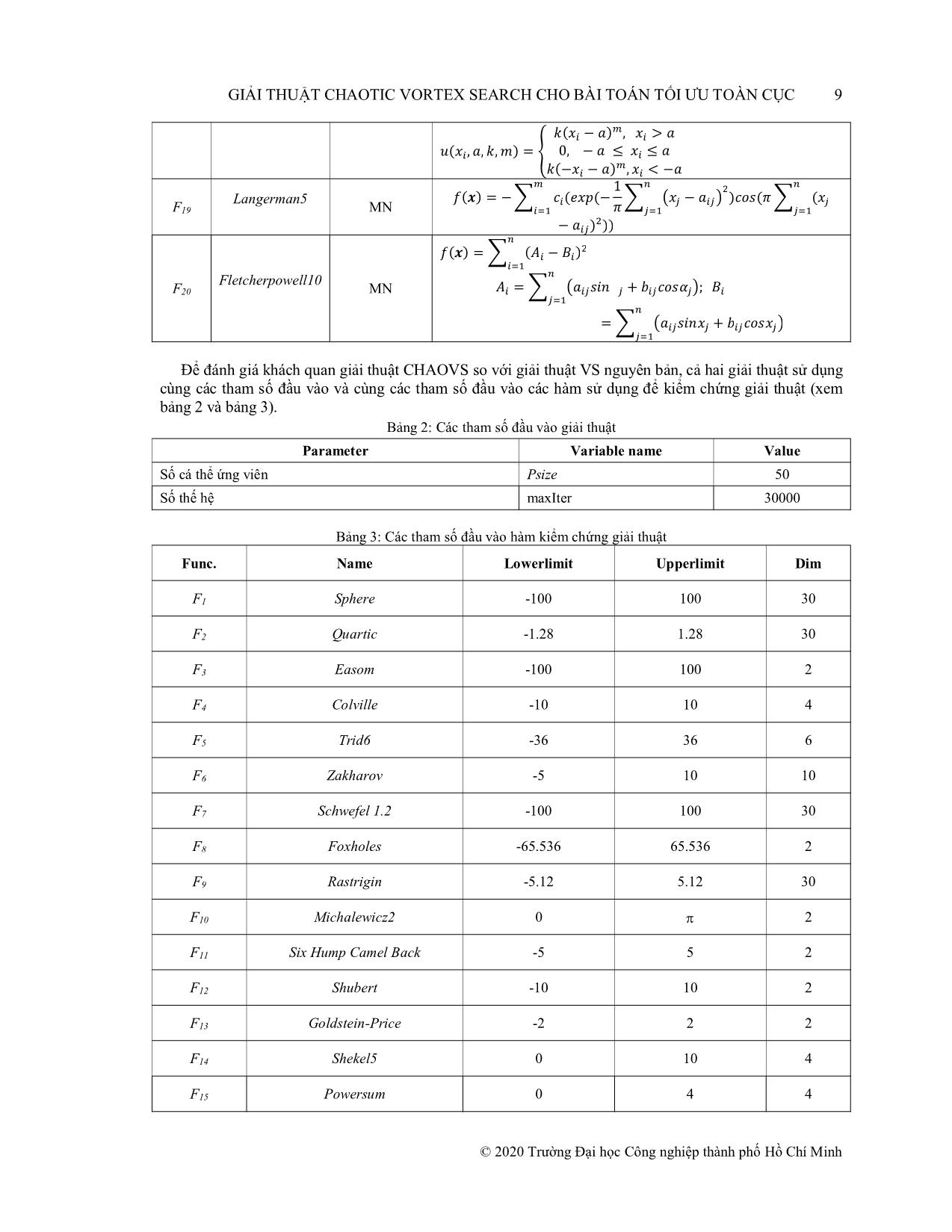
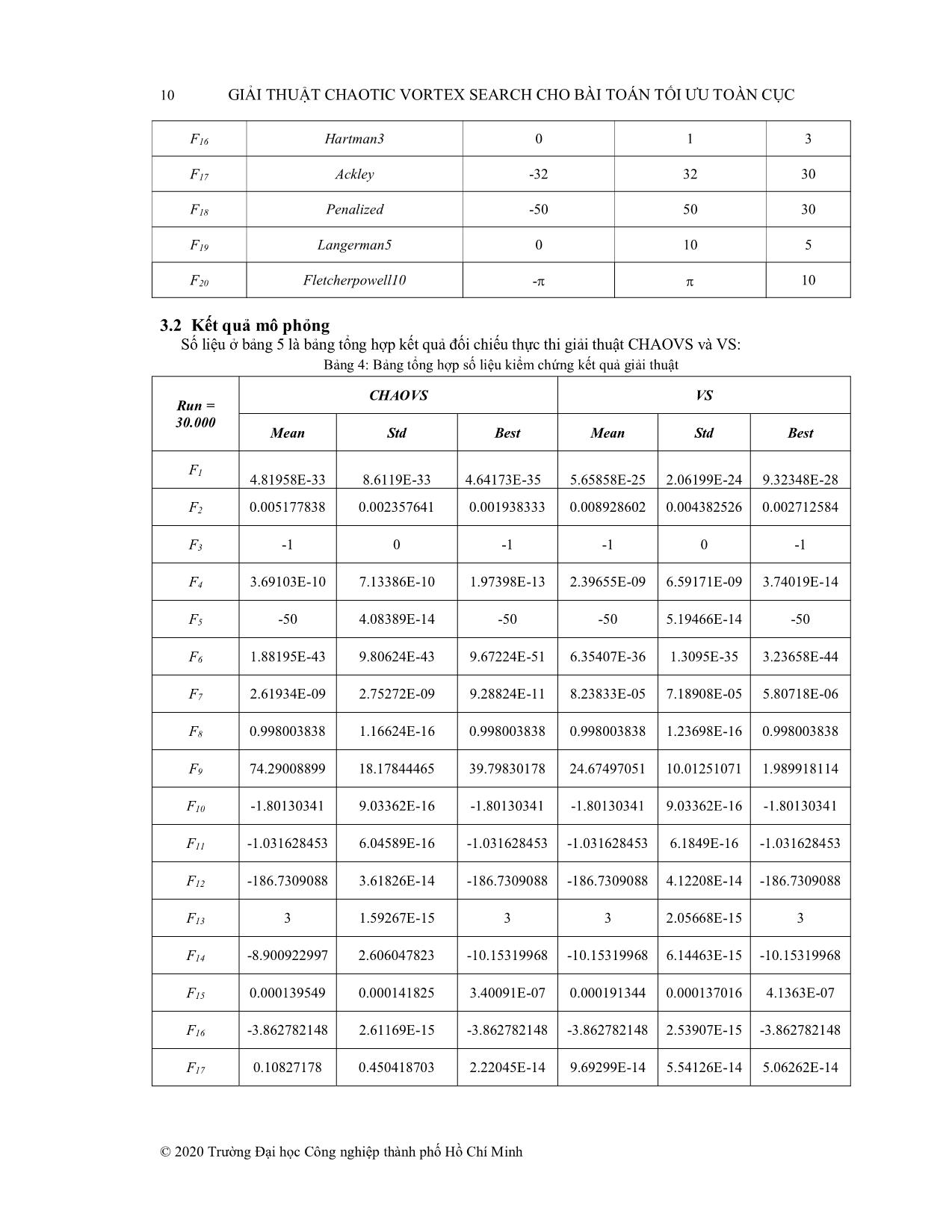
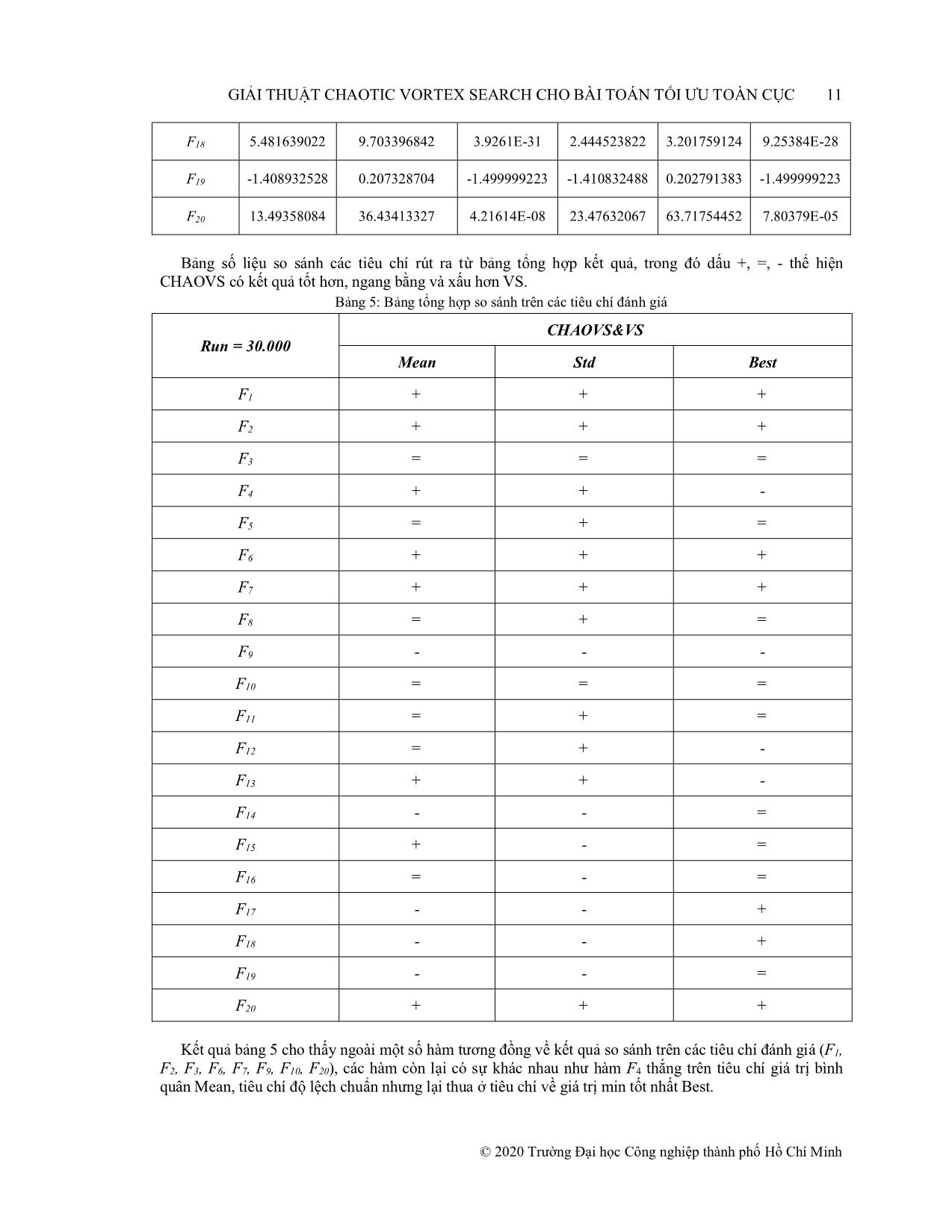
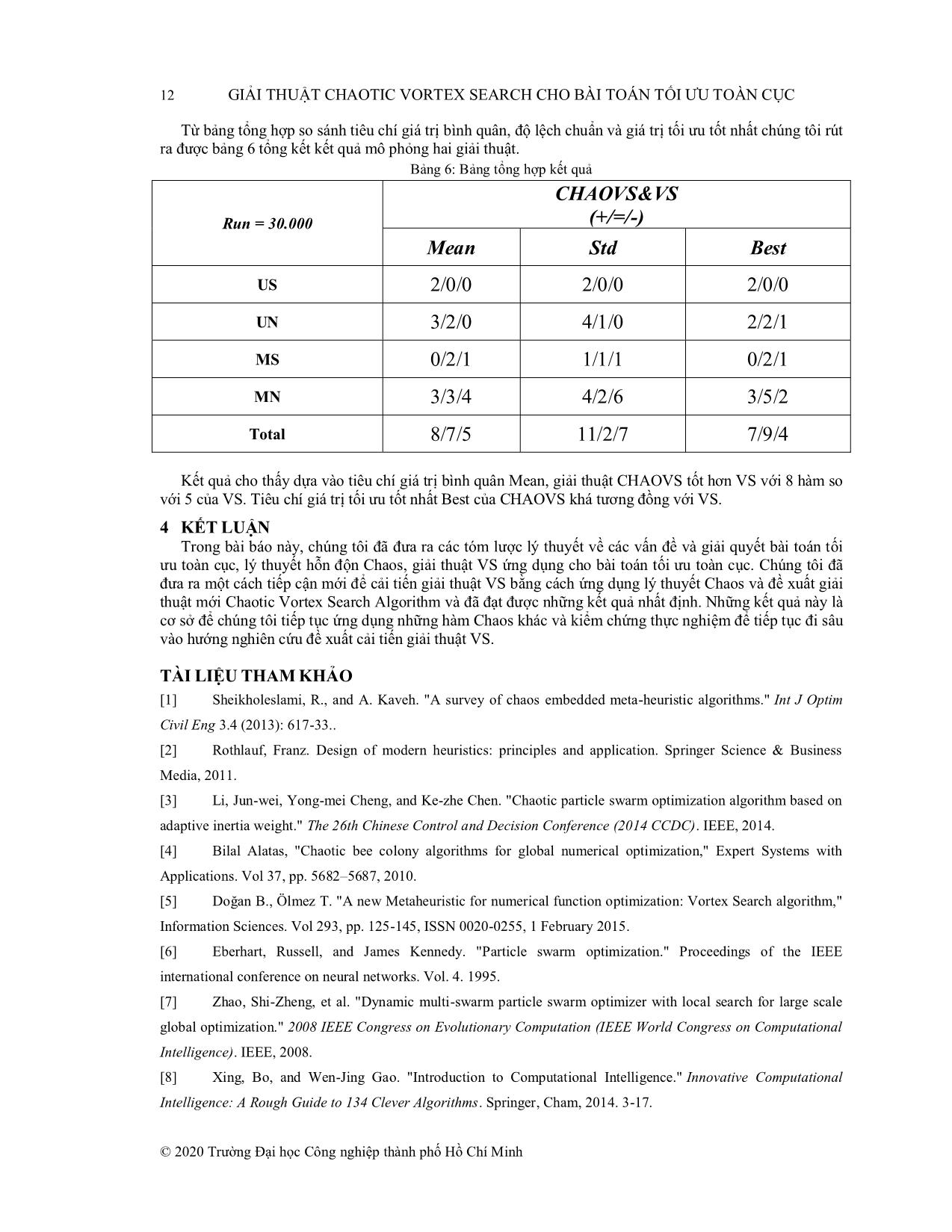
hát sinh tập ứng viên. 
 Hàm Chaotic được chọn là Bernoulli Map, được định nghĩa như sau: 
 s(n+1)= fB(s(n)) 
 Với điều kiện khởi tạo s(0) [-1,1] và fB là một ánh xạ chaotic fB: [-1,1] [-1,1] được định nghĩa: 
 fB(s)=   
   +  ; −1 ≤  < 
  
Trong đó tham số (-1,1). Giá trị s(0) và  được sử dụng cho mô phỏng kết quả là s(0) = 0.5 và = 0.8. 
   −  ;  ≤  ≤1
2.1 Quy luật phát sinh tập ứng viên Cs giải thuật VS 
Gọi μ0 là tâm tìm kiếm ban đầu, μt là tâm tìm kiếm thế hệ thứ t. 
 Khi đó tâm , D là số chiều không gian tìm kiếm 
 1 2 
 Trong đó:  =[0, 0,, 0 ] ; 
  
 [lowerlimiti, upperlimiti] là ràng buộc cận dưới và cận trên không gian chiều thứ i. Các cận dưới và cận 
trên trên tất cả các= chiều không gian với bộ hàm chuẩn Benchmark được thiết lập giá trị chung lowerlimit 
và upplimit (xem bảng 4). 
 Tại mỗi thế hệ tìm kiếm, sử dụng hàm quy luật phân phối chuẩn phát sinh ma trận CPsize,D có Psize dòng 
(kích thước quần thể) mỗi dòng chứa các giá trị số ngẫu nhiên theo quy luật phân phối Gauss (dựa theo 
công thức số (6), (7)) có giá trị trung bình Mean bằng 0, phương sai bằng 1: 
 C =   
  ⋯ 
 Ma trận C được sử dụng như một mặt nạ tìm ⋮kiếm để ⋱ xây dựng ⋮  ma trận công cụ tìm kiếm Ct cho tâm 
  
tìm kiếm Mean bằng 0 độ lệch chuẩn (là bán kính tìm⋯ kiếm thế hệ t): 
 
© 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
 GIẢI THUẬT CHAOTIC VORTEX SEARCH CHO BÀI TOÁN TỐI ƯU TOÀN CỤC 7 
   
  ⋯ 
 
 Trong đó bán kính ban đầu được tính= theo công⋮ thức ⋱ (2):  ⋮ 
  ⋯ 
  
 () − () 
 Bán kính tìm kiểm được điều chỉnh = giảm dần qua các thế hệ theo công thức điều chỉnh:
 ; Với 2 ; 
  
  = .  . (, )  = 1 à  =1− 
 MaxInt là số lượng thế hệ giải thuật thực hiện tìm kiếm. Tham số x được hiểu như độ uốn của hệ số 
giảm bán kính. (Tham số x được sử dụng cho mô phỏng giải thuật là x = 0.1) 
 Ma trận công cụ tìm kiếm Ct được dịch chuyển tới vị trí tâm tìm kiếm thực sự (với tâm tìm kiếm 
sử dụng để phát sinh tập ứng viên thế hệ t): 
  
 C(st) =     
  +  ⋯  + 
 Trong đó  ⋮ ⋱ là ⋮tâm tìm kiếm hiện tại sử dụng cho phát sinh tập ứng viên ở 
      
thế hệ mới C(st). +  1 2 ⋯  +  
  −1 −1 −1
 Đặt  =[ ;, các cá,, thể nếu] vi phạm ràng buộc về chiều không gian thứ i (ràng buộc cận 
dưới và cận trên) sẽ được thực hiện điều chỉnh theo công thức (3). 
  =  + 
 Sau khi thực hiện điều chỉnh các cá thể vi phạm, ta có tập cá thể ứng viên thế hệ t giải thuật VS (gọi là 
 VS
C (st) ): 
 VS
 C (st) =   
  ⋯ 
 VS
C (st) là một ma trận Psize×D trong đó Psize là kích⋮ thước ⋱ quần ⋮thể và D là số chiều không gian. Trong 
  
đó ( , chính là cá thể ứng viên thứ i trong⋯ tập quần thể Psize cá thể. 
    
2.2 Quy=  luật  ,,phát sinh) tập ứng viên Cs giải thuật CHAOVS 
 Sử dụng hàm Bernoulli map, phát sinh ma trận sử dụng để xây dựng quy luật phát sinh tập ứng viên 
mới: 
Bernoulli_map(Psize, D) =   trong đó các là các giá trị số Chaotic phát sinh từ 
  
  ⋯  
 
hàm Bernoulli map.   ⋮ ⋱ ⋮  
  VS 
 Chúng tôi thực hiện lai ghép với C ⋯(st) để tạo ra quy luật phát sinh tập ứng viên mới: 
 CHAOVS
 C (st) =     
   ⋯  
   ⋮ ⋱ ⋮  
3 KẾT QUẢ THỰC NGHIỆM ⋯ 
3.1 Đầu vào giải thuật 
 Để kiểm tra kết quả thực nghiệm để so sánh đối chiếu giải thuật cũ, chúng tôi kiểm chứng trên đầu vào 
là 20 hàm số lấy từ bộ dữ liệu Benchmark Function[16]. Kiểm chứng thực thi giải thuật được thực hiện 
trên phần mềm MATLAB R2013a, cấu hình máy CPU: Intel Core I5 5300u 2.3GHz, bộ nhớ đệm 3MB 
Cache, RAM: 8GB - DDR3 1600MHz. 
 Bộ 20 hàm kiểm chứng được chọn ngẫu nhiên nhưng chứa các đặc điểm khác nhau trong bộ hàm chuẩn 
Benchmark: U-Unimodal (Hàm đơn cực trị), M-Multimodal (Hàm đa cực trị), S-Seperable (Hàm phân tách 
được), N-Non_Seperable (Hàm không phân tách được). 
 © 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
8 GIẢI THUẬT CHAOTIC VORTEX SEARCH CHO BÀI TOÁN TỐI ƯU TOÀN CỤC 
Bảng 1: 20 Hàm Benchmark kiểm chứng kết quả giải thuật dựa vào U: Unimodal, M: Multimodal, S: Separable, N: 
 Non-Separable 
 C C: 
Func. Name Mô t 
 Characteristics ả
 F1 Sphere US  
 
 
 
 F2 Quartic US  () = ( ) 
 
 
 
 () = ( ) + random[0,1)
 F3 Easom UN  
  
  () = − () ()  (−( − ) − ( − ) )
 F4 Colville UN      
      
 () = 100( −  ) + ( − 1) + ( − 1) + 90( −  )
 + 10.1(( − 1) + ( − 1) )
 F5 Trid6 UN    
  + 19.8( −1)( − 1)
 
   
 F6 Zakharov UN  () = ( − 1) −   
   
   
 Schwefel 1.2   
 F7 UN () =  + (0.5 ) + (0.5  )
  
  
 () = | | + | |
 F8 Foxholes MS  
  
 1 1
 Rastrigin () =  +   
 F9 MS     
 500  + ∑  −  6
 
  
 Michalewicz2 () = [ − 10 ( 2 ) + 10]
 F10 MS 
  
 () = −   ()( (m =/ 10) )
 Six Hump 
 F MN 
 11 Camel Back 
   1   
 () = 4 − 2.1 +  +  − 4 + 4
  3 
 F12 Shubert MN 
  
 () =    (  + 1) +     ( + 1)
 +  
 
 F13 Goldstein-Price MN  
 1 + (  +  + 1) 
 () =        . 
 (19 − 14 + 3 − 14 + 6  + 3 )
 30 + (2 − 3)
 Shekel5    
 F14 MN (18 − 32 + 12 + 48 − 36 + 27 ) 
    
     
 () = −    −    −   +  
 F15 Powersum MN 
   
 
 ( )  
 F16 Hartman3 MN   =    (   ) −   
   
    
 () = −     exp −      −   
 
 F17 Ackley MN 1 
 () = −20exp (−0.2   )
     
 
 1 
 − exp (   cos (2 )) + 20 + 
  
 
    10 ( )
    
 F18 Penalized MN () =     
  +    ( − 1) [1 + 10 ( )] + ( − 1)
 
 
 +    ( , 10,100,4)
 1
  = 1 + ( + 1)
 4
© 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
 GIẢI THUẬT CHAOTIC VORTEX SEARCH CHO BÀI TOÁN TỐI ƯU TOÀN CỤC 9 
  
 ( − ) ,  > 
  
 ( , , , ) =  0, −  ≤  ≤ 
 Langerman5  
 F MN  (− − ) ,  < − 
 19 
  1   
 () = −   ( (−  −   ) ( (
  
  
  −  ) ))
 
 Fletcherpowell10  
 F MN () = ( −  )
 20 
      
  =    +   ;  
 
    
 =   +    
 Để đánh giá khách quan giải thuật CHAOVS so với giải thuật VS nguyên bản, cả hai giải thuật sử dụng 
cùng các tham số đầu vào và cùng các tham số đầu vào các hàm sử dụng để kiểm chứng giải thuật (xem 
bảng 2 và bảng 3). 
 Bảng 2: Các tham số đầu vào giải thuật 
 Parameter Variable name Value 
Số cá thể ứng viên Psize 50 
Số thế hệ maxIter 30000 
 Bảng 3: Các tham số đầu vào hàm kiểm chứng giải thuật 
 Func. Name Lowerlimit Upperlimit Dim 
 F1 Sphere -100 100 30 
 F2 Quartic -1.28 1.28 30 
 F3 Easom -100 100 2 
 F4 Colville -10 10 4 
 F5 Trid6 -36 36 6 
 F6 Zakharov -5 10 10 
 F7 Schwefel 1.2 -100 100 30 
 F8 Foxholes -65.536 65.536 2 
 F9 Rastrigin -5.12 5.12 30 
 F10 Michalewicz2 0 2 
 F11 Six Hump Camel Back -5 5 2 
 F12 Shubert -10 10 2 
 F13 Goldstein-Price -2 2 2 
 F14 Shekel5 0 10 4 
 F15 Powersum 0 4 4 
 © 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
10 GIẢI THUẬT CHAOTIC VORTEX SEARCH CHO BÀI TOÁN TỐI ƯU TOÀN CỤC 
 F16 Hartman3 0 1 3 
 F17 Ackley -32 32 30 
 F18 Penalized -50 50 30 
 F19 Langerman5 0 10 5 
 F20 Fletcherpowell10 - 10 
3.2 Kết quả mô phỏng 
 Số liệu ở bảng 5 là bảng tổng hợp kết quả đối chiếu thực thi giải thuật CHAOVS và VS: 
 Bảng 4: Bảng tổng hợp số liệu kiểm chứng kết quả giải thuật 
 CHAOVS VS 
 Run = 
 30.000 
 Mean Std Best Mean Std Best 
 F
 1 4.81958E-33 8.6119E-33 4.64173E-35 5.65858E-25 2.06199E-24 9.32348E-28 
 F2 0.005177838 0.002357641 0.001938333 0.008928602 0.004382526 0.002712584 
 F3 -1 0 -1 -1 0 -1 
 F4 3.69103E-10 7.13386E-10 1.97398E-13 2.39655E-09 6.59171E-09 3.74019E-14 
 F5 -50 4.08389E-14 -50 -50 5.19466E-14 -50 
 F6 1.88195E-43 9.80624E-43 9.67224E-51 6.35407E-36 1.3095E-35 3.23658E-44 
 F7 2.61934E-09 2.75272E-09 9.28824E-11 8.23833E-05 7.18908E-05 5.80718E-06 
 F8 0.998003838 1.16624E-16 0.998003838 0.998003838 1.23698E-16 0.998003838 
 F9 74.29008899 18.17844465 39.79830178 24.67497051 10.01251071 1.989918114 
 F10 -1.80130341 9.03362E-16 -1.80130341 -1.80130341 9.03362E-16 -1.80130341 
 F11 -1.031628453 6.04589E-16 -1.031628453 -1.031628453 6.1849E-16 -1.031628453 
 F12 -186.7309088 3.61826E-14 -186.7309088 -186.7309088 4.12208E-14 -186.7309088 
 F13 3 1.59267E-15 3 3 2.05668E-15 3 
 F14 -8.900922997 2.606047823 -10.15319968 -10.15319968 6.14463E-15 -10.15319968 
 F15 0.000139549 0.000141825 3.40091E-07 0.000191344 0.000137016 4.1363E-07 
 F16 -3.862782148 2.61169E-15 -3.862782148 -3.862782148 2.53907E-15 -3.862782148 
 F17 0.10827178 0.450418703 2.22045E-14 9.69299E-14 5.54126E-14 5.06262E-14 
© 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
 GIẢI THUẬT CHAOTIC VORTEX SEARCH CHO BÀI TOÁN TỐI ƯU TOÀN CỤC 11 
 F18 5.481639022 9.703396842 3.9261E-31 2.444523822 3.201759124 9.25384E-28 
 F19 -1.408932528 0.207328704 -1.499999223 -1.410832488 0.202791383 -1.499999223 
 F20 13.49358084 36.43413327 4.21614E-08 23.47632067 63.71754452 7.80379E-05 
 Bảng số liệu so sánh các tiêu chí rút ra từ bảng tổng hợp kết quả, trong đó dấu +, =, - thể hiện 
CHAOVS có kết quả tốt hơn, ngang bằng và xấu hơn VS. 
 Bảng 5: Bảng tổng hợp so sánh trên các tiêu chí đánh giá 
 CHAOVS&VS 
 Run = 30.000 
 Mean Std Best 
 F1 + + + 
 F2 + + + 
 F3 = = = 
 F4 + + - 
 F5 = + = 
 F6 + + + 
 F7 + + + 
 F8 = + = 
 F9 - - - 
 F10 = = = 
 F11 = + = 
 F12 = + - 
 F13 + + - 
 F14 - - = 
 F15 + - = 
 F16 = - = 
 F17 - - + 
 F18 - - + 
 F19 - - = 
 F20 + + + 
 Kết quả bảng 5 cho thấy ngoài một số hàm tương đồng về kết quả so sánh trên các tiêu chí đánh giá (F1, 
F2, F3, F6, F7, F9, F10, F20), các hàm còn lại có sự khác nhau như hàm F4 thắng trên tiêu chí giá trị bình 
quân Mean, tiêu chí độ lệch chuẩn nhưng lại thua ở tiêu chí về giá trị min tốt nhất Best. 
 © 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
12 GIẢI THUẬT CHAOTIC VORTEX SEARCH CHO BÀI TOÁN TỐI ƯU TOÀN CỤC 
 Từ bảng tổng hợp so sánh tiêu chí giá trị bình quân, độ lệch chuẩn và giá trị tối ưu tốt nhất chúng tôi rút 
ra được bảng 6 tổng kết kết quả mô phỏng hai giải thuật. 
 Bảng 6: Bảng tổng hợp kết quả 
 CHAOVS&VS 
 Run = 30.000 (+/=/-) 
 Mean Std Best 
 US 2/0/0 2/0/0 2/0/0 
 UN 3/2/0 4/1/0 2/2/1 
 MS 0/2/1 1/1/1 0/2/1 
 MN 3/3/4 4/2/6 3/5/2 
 Total 8/7/5 11/2/7 7/9/4 
 Kết quả cho thấy dựa vào tiêu chí giá trị bình quân Mean, giải thuật CHAOVS tốt hơn VS với 8 hàm so 
với 5 của VS. Tiêu chí giá trị tối ưu tốt nhất Best của CHAOVS khá tương đồng với VS. 
4 KẾT LUẬN 
 Trong bài báo này, chúng tôi đã đưa ra các tóm lược lý thuyết về các vấn đề và giải quyết bài toán tối 
ưu toàn cục, lý thuyết hỗn độn Chaos, giải thuật VS ứng dụng cho bài toán tối ưu toàn cục. Chúng tôi đã 
đưa ra một cách tiếp cận mới để cải tiến giải thuật VS bằng cách ứng dụng lý thuyết Chaos và đề xuất giải 
thuật mới Chaotic Vortex Search Algorithm và đã đạt được những kết quả nhất định. Những kết quả này là 
cơ sở để chúng tôi tiếp tục ứng dụng những hàm Chaos khác và kiểm chứng thực nghiệm để tiếp tục đi sâu 
vào hướng nghiên cứu đề xuất cải tiến giải thuật VS. 
TÀI LIỆU THAM KHẢO 
[1] Sheikholeslami, R., and A. Kaveh. "A survey of chaos embedded meta-heuristic algorithms." Int J Optim 
Civil Eng 3.4 (2013): 617-33.. 
[2] Rothlauf, Franz. Design of modern heuristics: principles and application. Springer Science & Business 
Media, 2011. 
[3] Li, Jun-wei, Yong-mei Cheng, and Ke-zhe Chen. "Chaotic particle swarm optimization algorithm based on 
adaptive inertia weight." The 26th Chinese Control and Decision Conference (2014 CCDC). IEEE, 2014. 
[4] Bilal Alatas, "Chaotic bee colony algorithms for global numerical optimization," Expert Systems with 
Applications. Vol 37, pp. 5682–5687, 2010. 
[5] Doğan B., Ölmez T. "A new Metaheuristic for numerical function optimization: Vortex Search algorithm," 
Information Sciences. Vol 293, pp. 125-145, ISSN 0020-0255, 1 February 2015. 
[6] Eberhart, Russell, and James Kennedy. "Particle swarm optimization." Proceedings of the IEEE 
international conference on neural networks. Vol. 4. 1995. 
[7] Zhao, Shi-Zheng, et al. "Dynamic multi-swarm particle swarm optimizer with local search for large scale 
global optimization." 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational 
Intelligence). IEEE, 2008. 
[8] Xing, Bo, and Wen-Jing Gao. "Introduction to Computational Intelligence." Innovative Computational 
Intelligence: A Rough Guide to 134 Clever Algorithms. Springer, Cham, 2014. 3-17. 
© 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh 
 GIẢI THUẬT CHAOTIC VORTEX SEARCH CHO BÀI TOÁN TỐI ƯU TOÀN CỤC 13 
[9] Mitchell, Melanie, "An Introdution to Genetic Algorithms," Cambridge, MA: MIT Press, ISBN 
9780585030944, 1996. 
[10] Granville, Vincent, Mirko Krivánek, and J-P. Rasson. "Simulated annealing: A proof of 
convergence." IEEE transactions on pattern analysis and machine intelligence 16.6 (1994): 652-656. 
[11] Rastrigin L.A.. "The convergence of the random search method in the extremal control of a many 
parameter system," Automation and Remote Control. Vol 24 (10), pp. 1337–1342, 1963. 
[12] Hooke R., Jeeves T. A. "Direct search” solution of numerical and statistical problems,'' Journal of the 
Association for Computing Machinery (ACM). Vol 8 (2), pp. 212–229, 1961. 
[13] Doğan B., Ölmez T. "Modified Off-lattice AB Model for Protein Folding Problem Using the Vortex Search 
Algorithm," International Journal of Machine Learning and Computing. Vol. 5(4), pp. 329-333, 2015. 
[14] Dang, Binh Thanh, Minh Cong Vo, and Tung Khac Truong. "Social spider algorithm-based spectrum 
allocation optimization for cognitive radio networks." International Journal of Applied Engineering Research 12.13 
(2017): 3879-3887. 
[15] Diacu, Florin, and Philip Holmes. Celestial encounters: the origins of chaos and stability. Vol. 22. 
Princeton University Press, 1999. 
[16] Liang, J. J., B. Y. Qu, and P. N. Suganthan. "Problem definitions and evaluation criteria for the CEC 2014 
special session and competition on single objective real-parameter numerical optimization." Computational 
Intelligence Laboratory, Zhengzhou University, Zhengzhou China and Technical Report, Nanyang Technological 
University, Singapore 635 (2013). 
 Ngày nhận bài: 29/03/2019 
 Ngày chấp nhận đăng: 03/01/2020 
 © 2020 Trường Đại học Công nghiệp thành phố Hồ Chí Minh