Experimental investigation of hydrodynamic phenomena in vertical-upward adiabatic two-phase Flow Conditions

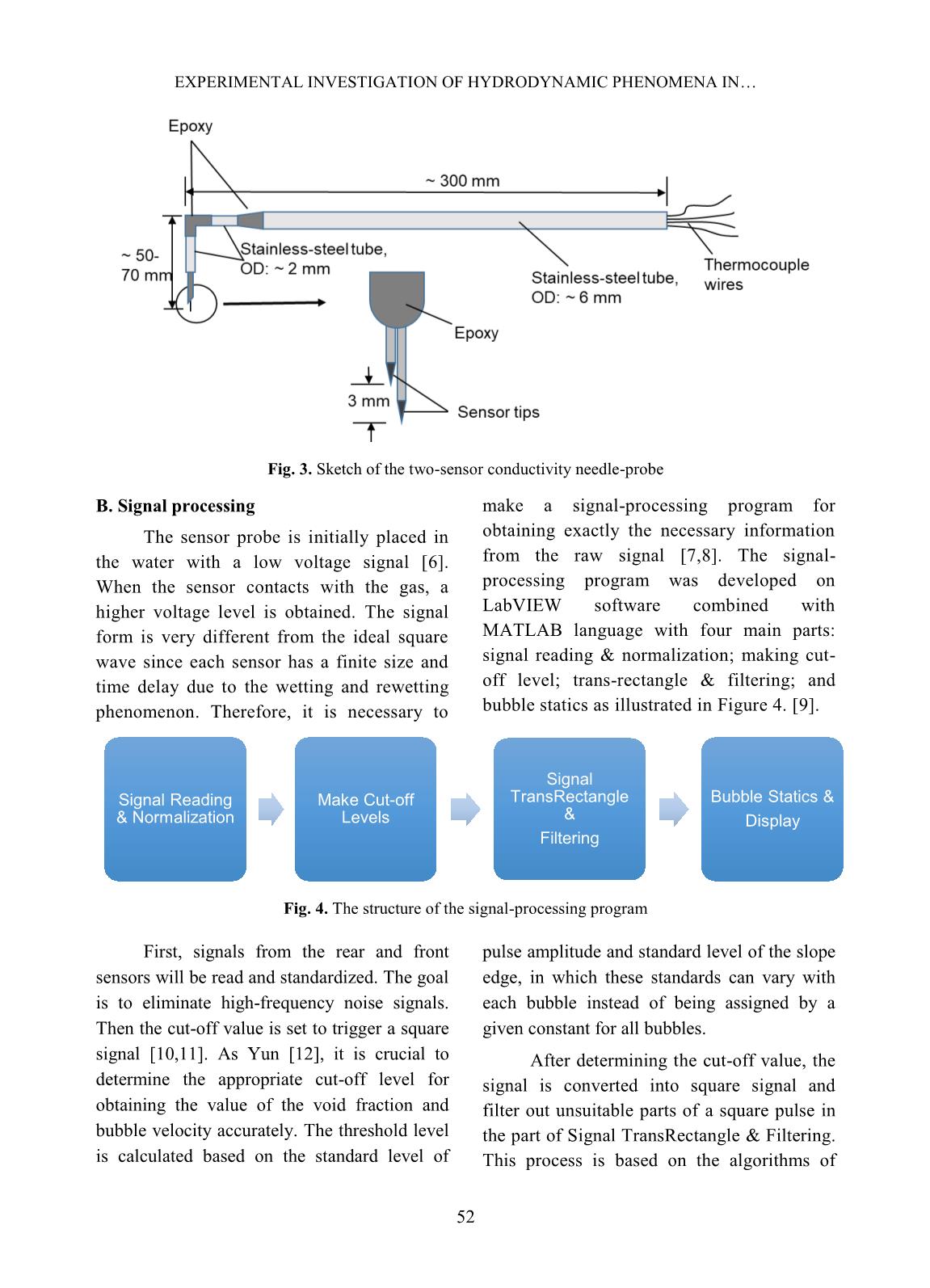
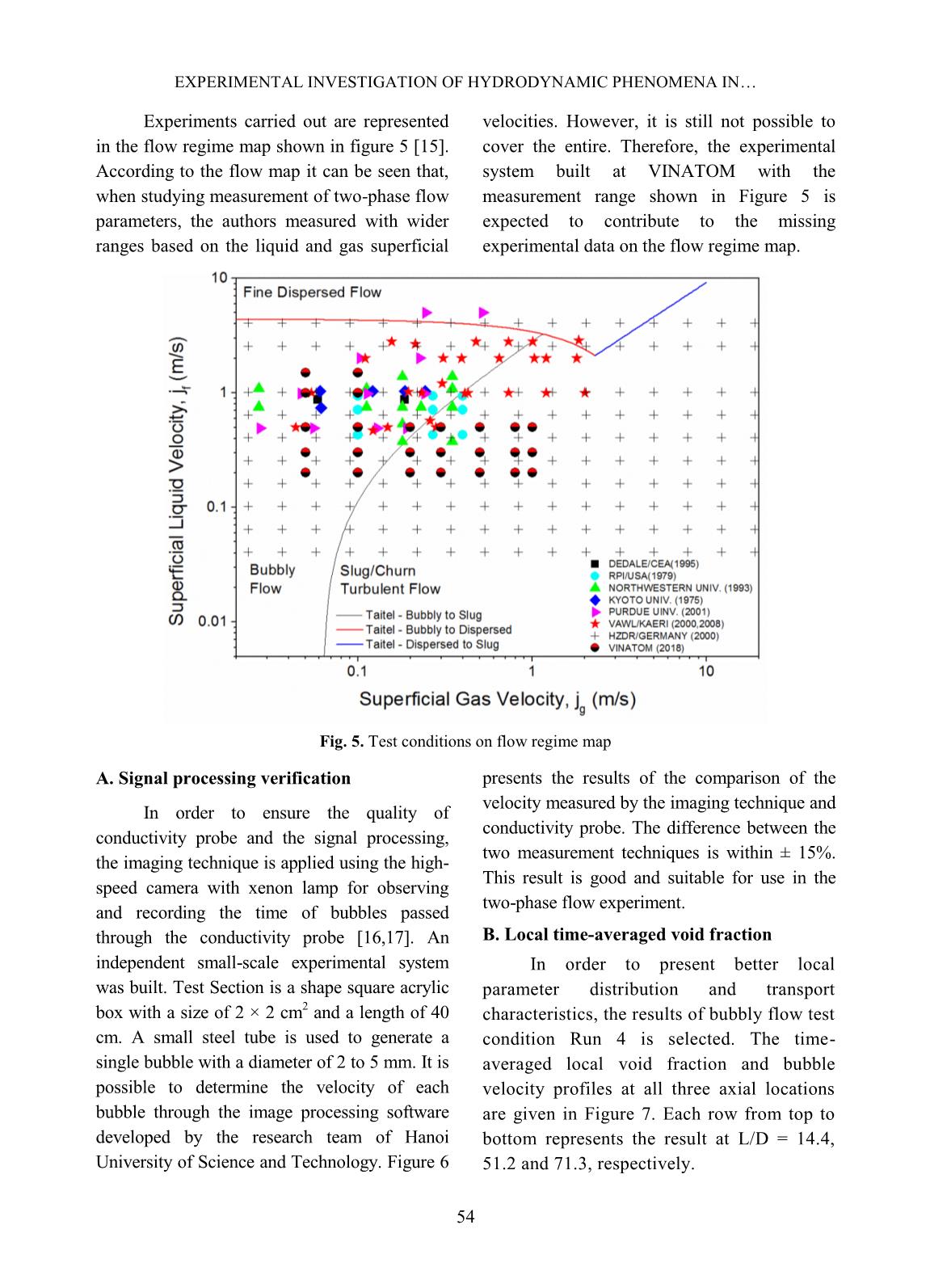
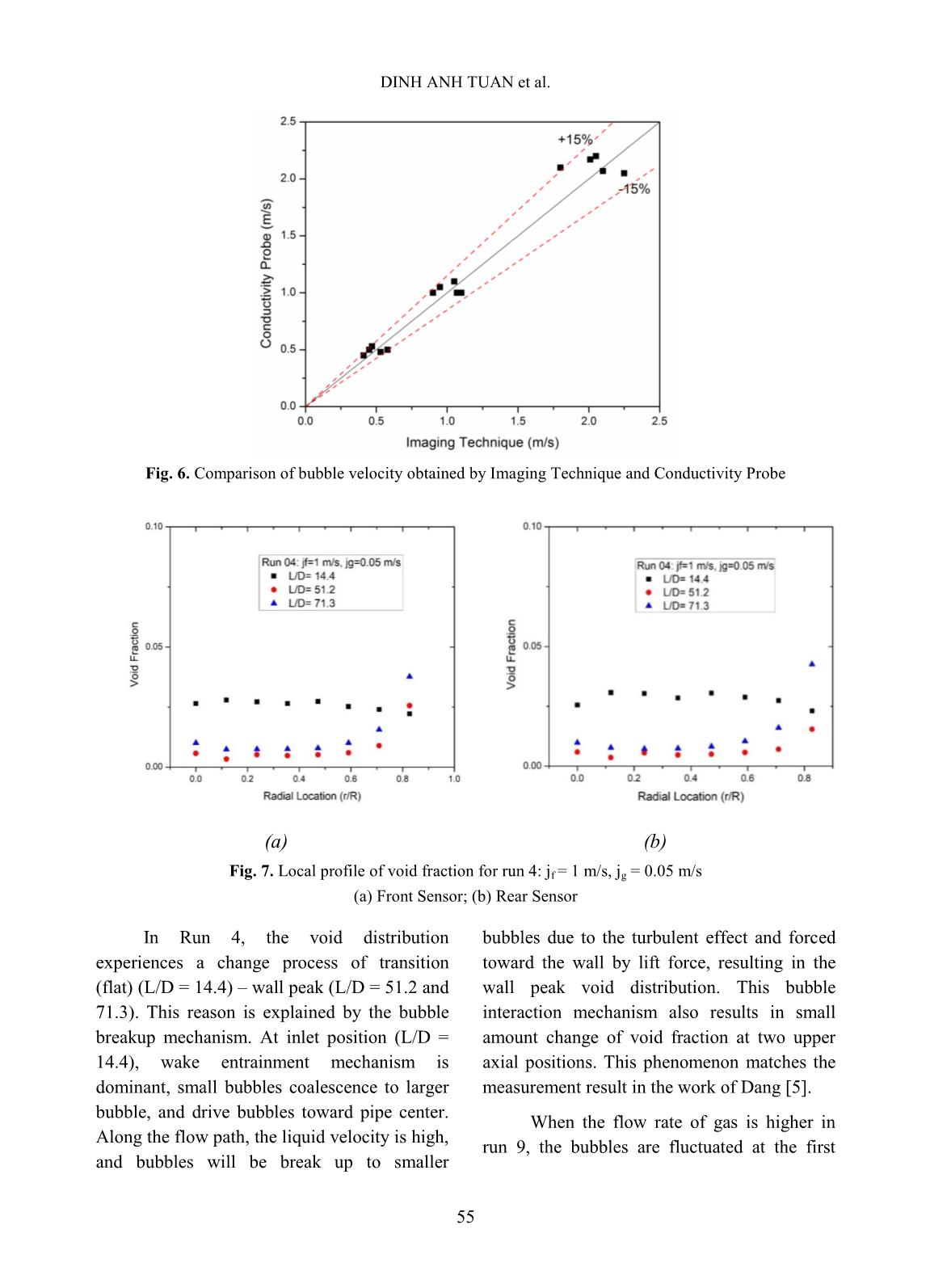
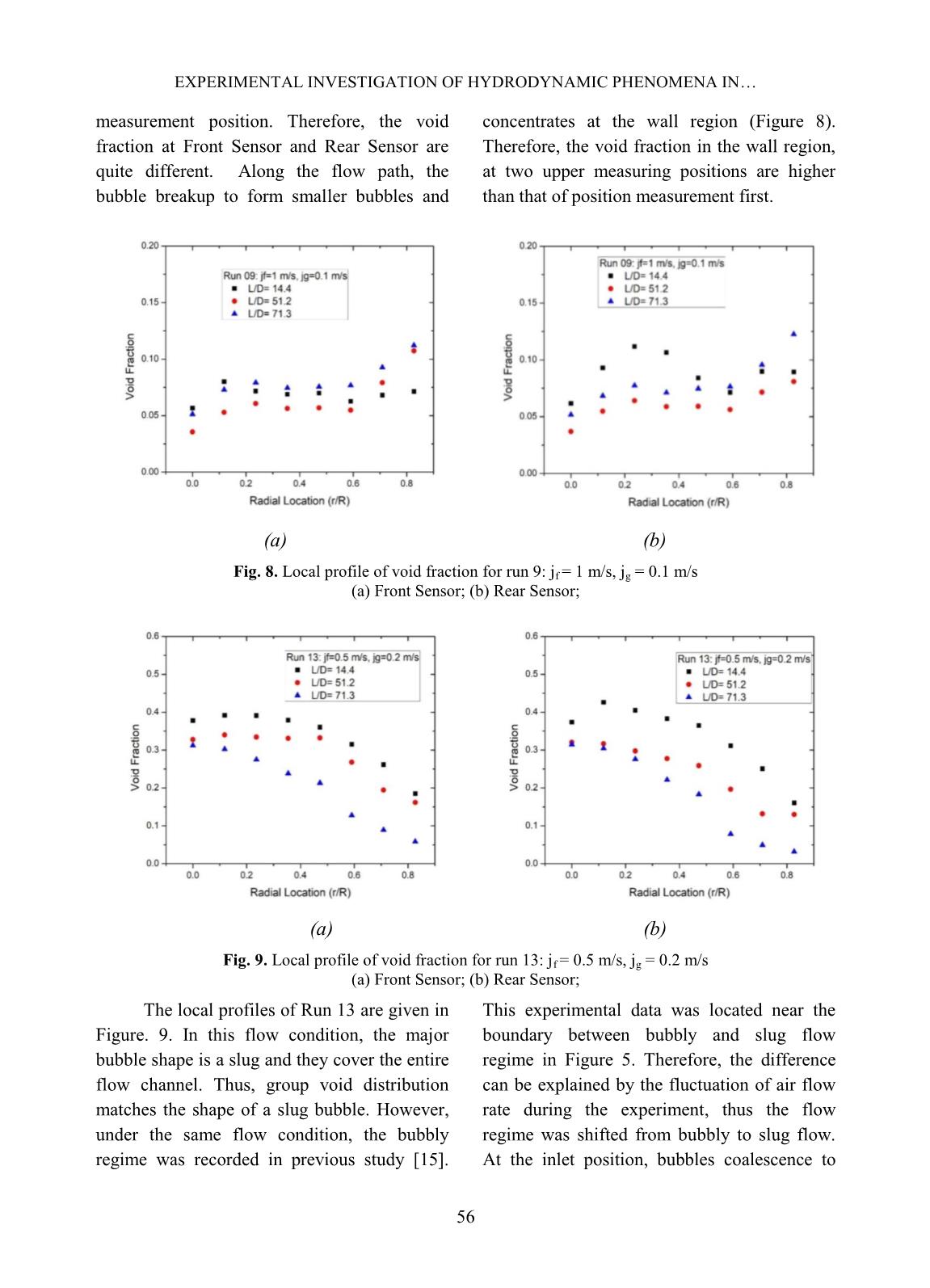
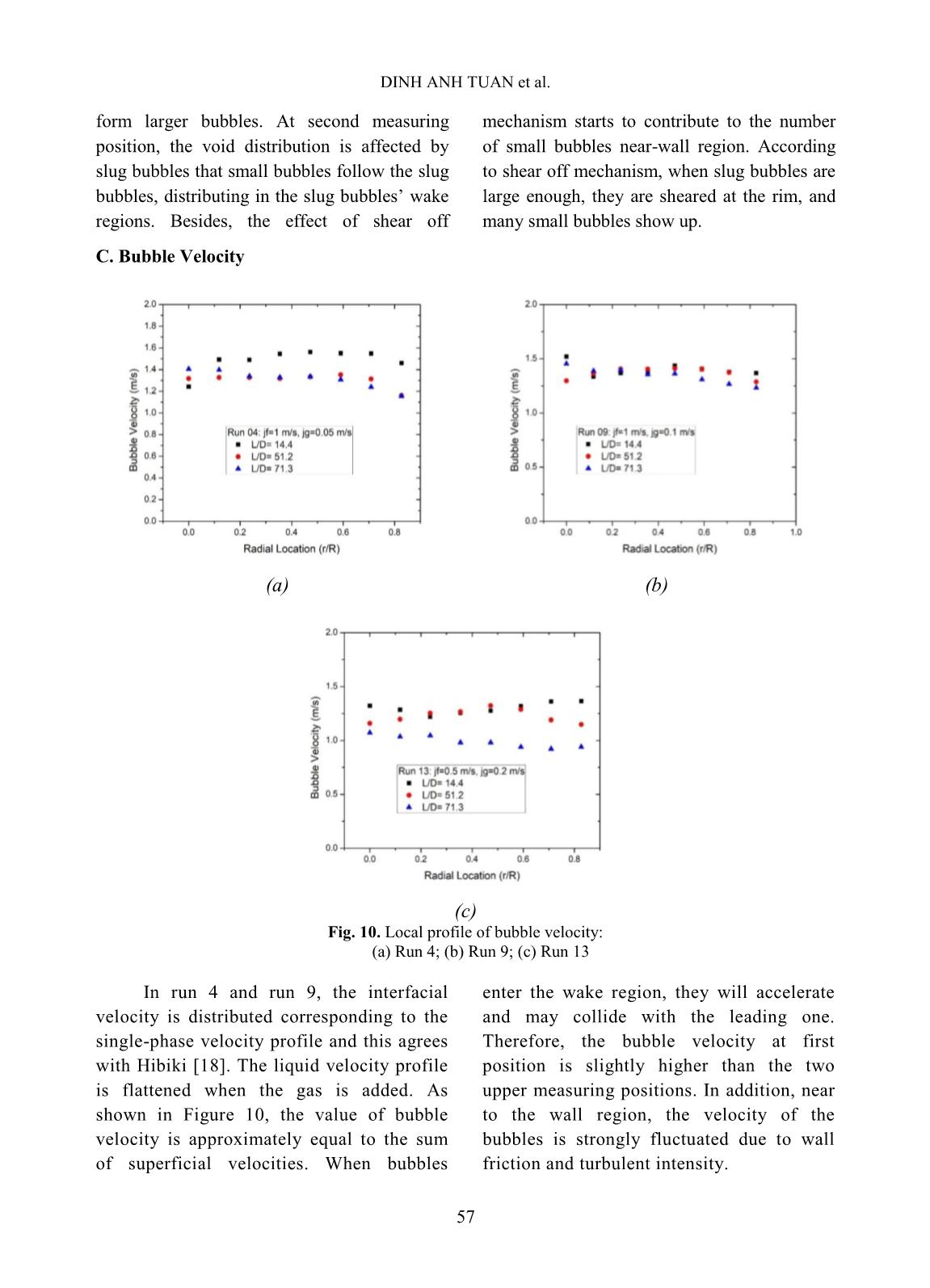
t of Signal TransRectangle & Filtering. 
This process is based on the algorithms of 
Signal Reading 
& Normalization 
Make Cut-off 
Levels 
Signal 
TransRectangle 
& 
Filtering 
Bubble Statics & 
Display 
DINH ANH TUAN et al. 
53 
Yun [12] and Euh [13]. Finally, the two-phase 
flow parameters are calculated in the part of 
Bubble Statics. 
From the square wave signal, the 
number of bubbles that hit the sensor can be 
measured by counting the number of pulses in 
the signal. The interfacial velocity of each 
interface can be obtained by using the 
distance to the different tips of the two-sensor 
probe and the time delay between the 
upstream and downstream signals. The 
parameters of the two-phase flow have been 
calculated as below [14]. 
- The time-averaged void fraction: 
The time-averaged void fraction is a 
function of the total sampling time - Ω, and the 
accumulated pulse widths of the upstream 
sensor during the sampling period. Thus, this 
time-averaged void fraction is simply the 
accumulated time the sensor is exposed to the 
gas phase divided by the total sampling time of 
the sensor. 
 ̅ 
∑ 
Where, Nt is the number of bubbles that 
strike the sensor; (tTF – tTR)j is the time that the 
sensor is exposed to the gas phase. 
- The time-averaged interfacial velocity: 
The interfacial velocity can be computed 
by taking into account the span among the tips 
of the front and rear sensor and the time 
difference between the front and rear signals. 
Thus, the time-averaged interfacial velocity is 
given as: 
| ⃗ | 
∑
Where Δs is the distance between the 
front and rear sensor; tRR – tTR is the relative 
time between the bubble striking the front and 
rear sensor. 
IV. PRELIMINARY RESULTS AND DISCUSSION 
Experiment data was collected at 8 radial 
measurement points with each point distance of 
1.5 mm along three axial positions (L/D = 
14.4, L/D = 51.2, L/D = 71.3). All the flow 
conditions are summarized in Table I. 
Table I. Experimental flow condition 
Parameter Run 
1-5 
Run 
6 -10 
Run 
11-13 
Run 
14-16 
Run 
17-19 
Run 
20-22 
Run 
23-25 
Superficial gas 
velocity, jg [m/s] 
0.05 0.10 0.20 0.30 0.50 0.80 1.00 
Superficial water 
velocity, jf [m/s] 
0.2 
0.3 
0.5 
1.0 
1.5 
0.2 
0.3 
0.5 
1.0 
1.5 
0.2 
0.3 
0.5 
0.2 
0.3 
0.5 
0.2 
0.3 
0.5 
0.2 
0.3 
0.5 
0.2 
0.3 
0.5 
(1) 
(2) 
EXPERIMENTAL INVESTIGATION OF HYDRODYNAMIC PHENOMENA IN 
54 
Experiments carried out are represented 
in the flow regime map shown in figure 5 [15]. 
According to the flow map it can be seen that, 
when studying measurement of two-phase flow 
parameters, the authors measured with wider 
ranges based on the liquid and gas superficial 
velocities. However, it is still not possible to 
cover the entire. Therefore, the experimental 
system built at VINATOM with the 
measurement range shown in Figure 5 is 
expected to contribute to the missing 
experimental data on the flow regime map. 
Fig. 5. Test conditions on flow regime map 
A. Signal processing verification 
In order to ensure the quality of 
conductivity probe and the signal processing, 
the imaging technique is applied using the high-
speed camera with xenon lamp for observing 
and recording the time of bubbles passed 
through the conductivity probe [16,17]. An 
independent small-scale experimental system 
was built. Test Section is a shape square acrylic 
box with a size of 2 × 2 cm
2
 and a length of 40 
cm. A small steel tube is used to generate a 
single bubble with a diameter of 2 to 5 mm. It is 
possible to determine the velocity of each 
bubble through the image processing software 
developed by the research team of Hanoi 
University of Science and Technology. Figure 6 
presents the results of the comparison of the 
velocity measured by the imaging technique and 
conductivity probe. The difference between the 
two measurement techniques is within ± 15%. 
This result is good and suitable for use in the 
two-phase flow experiment. 
B. Local time-averaged void fraction 
In order to present better local 
parameter distribution and transport 
characteristics, the results of bubbly flow test 
condition Run 4 is selected. The time-
averaged local void fraction and bubble 
velocity profiles at all three axial locations 
are given in Figure 7. Each row from top to 
bottom represents the result at L/D = 14.4, 
51.2 and 71.3, respectively. 
DINH ANH TUAN et al. 
55 
Fig. 6. Comparison of bubble velocity obtained by Imaging Technique and Conductivity Probe 
(a) (b) 
Fig. 7. Local profile of void fraction for run 4: jf = 1 m/s, jg = 0.05 m/s 
(a) Front Sensor; (b) Rear Sensor 
In Run 4, the void distribution 
experiences a change process of transition 
(flat) (L/D = 14.4) – wall peak (L/D = 51.2 and 
71.3). This reason is explained by the bubble 
breakup mechanism. At inlet position (L/D = 
14.4), wake entrainment mechanism is 
dominant, small bubbles coalescence to larger 
bubble, and drive bubbles toward pipe center. 
Along the flow path, the liquid velocity is high, 
and bubbles will be break up to smaller 
bubbles due to the turbulent effect and forced 
toward the wall by lift force, resulting in the 
wall peak void distribution. This bubble 
interaction mechanism also results in small 
amount change of void fraction at two upper 
axial positions. This phenomenon matches the 
measurement result in the work of Dang [5]. 
When the flow rate of gas is higher in 
run 9, the bubbles are fluctuated at the first 
EXPERIMENTAL INVESTIGATION OF HYDRODYNAMIC PHENOMENA IN 
56 
measurement position. Therefore, the void 
fraction at Front Sensor and Rear Sensor are 
quite different. Along the flow path, the 
bubble breakup to form smaller bubbles and 
concentrates at the wall region (Figure 8). 
Therefore, the void fraction in the wall region, 
at two upper measuring positions are higher 
than that of position measurement first. 
(a) (b) 
Fig. 8. Local profile of void fraction for run 9: jf = 1 m/s, jg = 0.1 m/s 
(a) Front Sensor; (b) Rear Sensor; 
(a) (b) 
Fig. 9. Local profile of void fraction for run 13: jf = 0.5 m/s, jg = 0.2 m/s 
(a) Front Sensor; (b) Rear Sensor; 
The local profiles of Run 13 are given in 
Figure. 9. In this flow condition, the major 
bubble shape is a slug and they cover the entire 
flow channel. Thus, group void distribution 
matches the shape of a slug bubble. However, 
under the same flow condition, the bubbly 
regime was recorded in previous study [15]. 
This experimental data was located near the 
boundary between bubbly and slug flow 
regime in Figure 5. Therefore, the difference 
can be explained by the fluctuation of air flow 
rate during the experiment, thus the flow 
regime was shifted from bubbly to slug flow. 
At the inlet position, bubbles coalescence to 
DINH ANH TUAN et al. 
57 
form larger bubbles. At second measuring 
position, the void distribution is affected by 
slug bubbles that small bubbles follow the slug 
bubbles, distributing in the slug bubbles’ wake 
regions. Besides, the effect of shear off 
mechanism starts to contribute to the number 
of small bubbles near-wall region. According 
to shear off mechanism, when slug bubbles are 
large enough, they are sheared at the rim, and 
many small bubbles show up. 
C. Bubble Velocity 
(a) (b) 
(c) 
Fig. 10. Local profile of bubble velocity: 
(a) Run 4; (b) Run 9; (c) Run 13 
In run 4 and run 9, the interfacial 
velocity is distributed corresponding to the 
single-phase velocity profile and this agrees 
with Hibiki [18]. The liquid velocity profile 
is flattened when the gas is added. As 
shown in Figure 10, the value of bubble 
velocity is approximately equal to the sum 
of superficial velocities. When bubbles 
enter the wake region, they will accelerate 
and may collide with the leading one. 
Therefore, the bubble velocity at first 
position is slightly higher than the two 
upper measuring positions. In addition, near 
to the wall region, the velocity of the 
bubbles is strongly fluctuated due to wall 
friction and turbulent intensity. 
EXPERIMENTAL INVESTIGATION OF HYDRODYNAMIC PHENOMENA IN 
58 
In Run 13, the channel-averaged velocity 
at the higher measuring positions are gradually 
decreased and are distributed almost uniformly 
in the radius. This phenomenon occurs in the 
case of low water superficial velocity, and drag 
force is domination. As the bubble grows, the 
bubble is normally accelerated by the effect of 
buoyancy force. However, due to the effect of 
drag force, velocity in run 13 is suitable. 
V. CONCLUSIONS 
The experimental investigation on local 
interfacial parameters for vertical upward air-
water two-phase flow was performed in this 
study. Two-sensor conductivity probe was used 
for the measurement of 25 flow conditions that 
covers from bubbly flow to slug flow. The 
local parameters included are a time-averaged 
void fraction and bubble interfacial velocity. 
The data acquisition frequency of 10 kHz and 
the sampling time of 60 s were applied. 
From the local experimental results, the 
profiles of void fraction and interfacial velocity 
along the axial and radial of the flow channel 
were discussed in detail. The bubble 
interaction mechanisms caused the differences 
in local parameter distribution. For high liquid 
superficial velocity (jf), the effect of buoyancy 
force is dominant, and bubble break up 
phenomena is observed. On the contrary, for 
low liquid superficial velocity (jf), the effect of 
drag force is dominant and bubble interaction 
mechanism will change from bubble break up 
to bubble coalescence. 
When changing the flow conditions, the 
void fraction distribution changes from wall 
peaking at Run 4 and Run 9 to center peak at 
Run 13. The reason might be due to the 
uncertainties in the measured results that need 
to be carefully considered and reduced in 
future works. In conclusion, the test facility, 
the experimental methods, and the preliminary 
experimental results obtained in this study can 
be helpful to study and comprehend the 
fundamental two-phase flow phenomena. For 
practical application in nuclear reactor safety, 
they are envisaged to be further improved and 
applied to verification and validation of 
calculation methods and codes, e.g., CFD 
codes, in modeling of two-phase flow. 
NOMENCLATURE 
D – pipe diameter 
g – acceleration of gravity 
L – length 
lchord – chord length 
N – number of bubble 
p – pressure 
t – time 
tdelay – delay time 
u – velocity 
V – Volume 
Greek Symbols 
α – void fraction 
µ – viscosity 
ρ – density 
σ – deviation standard 
Ω – total sampling time 
Subscripts 
b – bubble 
f – liquid 
g – gas 
ACKNOWLEDGEMENT 
This work was performed at Institute of 
Nuclear Science and Technology, Vietnam 
Atomic Energy Institute under the project 
“Construction of Thermal-hydraulic Experiment 
and Investigation of Hydrodynamic Phenomena 
of Two-phase Flow”, grant code 
DTCB.17/16/VKHKTHN. The authors would 
like to thank Ministry of Science and 
Technology for their support on this project. 
REFERENCES 
[1]. L.S. Tong and Y.S. Tang., Boiling Heat 
Transfer And Two-Phase Flow (Series in 
DINH ANH TUAN et al. 
59 
Chemical and Mechanical Engineering), CRC 
Press (book), 1997. 
[2]. L.G. Neal and S.G. Bankoff., A high resolution 
resistivity probe for determination of local 
void properties in gas-liquid flow. AIChEJ (9) 
490-494, 1963. 
[3]. M. Walter., Study on interfacial area transport in 
vertical bubbly flows, Ingenieur Thesis, Korea 
Atomic Energy Research Institute, Korea, 2008. 
[4]. A. Manera, B. Ozar, S. Paranjape, M. Ishii, H.-
M. Prasser., Comparison between wire-mesh 
sensors and conductive needle-probes for 
measurements of two-phase flow parameters, 
Nuclear Engineering and Design (239) 1718–
1724, 2009. 
[5]. Z. Dang, G. Wang, P. Ju, X. Yang, R. Bean, 
M. Ishii, S. Bajorek, M. Bernard., 
Experimental study of interfacial 
characteristics of vertical upward air-water 
two-phase flow in 25.4 mm ID round pipe. 
International Journal of Heat and Mass 
Transfer (108) 1825–1838, 2017. 
[6]. K. Sekoguchi, H. Fukui, M. Tsutsui and K. 
Nishikawa., Investigation into the statistical 
characteristics of bubbles in two-phase flow 
(2nd Report, Application and establishment of 
electrical resistivity probe method), Bull. 
JSME (18) 397-404, 1975. 
[7]. M.S. Hoffer and W. Resnick., A modified 
electro resistivity probe technique for steady- 
and unsteady-state measurements in fine 
dispersions – I. Hardware and practical aspects, 
Chem. Engng. Sci. (30) 473-480, 1975. 
[8]. J.M. Burgess and P.H. Calderbank., The 
measurement of bubble parameters in two-
phase dispersions-I. The development of an 
improved probe techniques, Chem. Engng Sci. 
(30) 743-750, 1975. 
[9]. M. Behnia, S.J., Gillespie., Void fraction 
measurement by a computerized double-point 
resistivity probe. Flow. Meas. Instrum. (2) 
243-247, 1991. 
[10]. W.H. Leung, S.T. Revankar, Y. Ishii and M. 
Ishii., Axial development of interfacial area 
and void concentration profiles measured by 
double-sensor probe method, Int. J. Heat Mass 
Transfer (38) 445-453, 1995. 
[11]. X. Zhao, G. Lucas, and S. Pradhan., Signal 
Processing method in using four-sensor probe 
for measuring the velocity vector of air-liquid 
two phase flow. Journal of the Japanese 
Society of Experimental Mechanics (JSEM) 
(9) 19-24, 2009. 
[12]. B.J. Yun, K.H. Kim, G.C. Park, C.H. Chung,, 
A study on the Measurement of Local Void 
Fraction. Journal of the Korean Nuclear 
Society 24(2) 168-177, 1992. 
[13]. D.J. Euh, B.J. Yun, C.H. Song, T.S. Kwon, 
M.K. Chung, U.C. Lee., Development of the 
five-sensor conductivity probe method for the 
measurement of the interfacial are 
concentration, Nuclear Engineering and 
Design (205) 35-51, 2001. 
[14]. I. Kataoka and A. Serizawa., Averaged bubble 
diameter and interfacial area in bubbly flow, 
Proc. 5th Two-phase Symp. Japan, Kobe, 
Japan, 28-29 November 77-80, 1984. 
[15]. Y. Taitel, D. Bornea and A. E. Dukler., 
Modelling Flow Pattern Transitions for Steady 
Upward Gas-Liquid Flow in Vertical Tubes, 
AlChE Journal (Vol. 26, No. 3) 345–354, 1980. 
[16]. M. Ishii and S. Kim., Micro four-sensor probe 
measurement of interfacial area transport for 
bubbly flow in round pipes. Nuclear 
Engineering and Design 205 123-131, 2001. 
[17]. M. McCreary., Design and Testing 
Conductivity Probes for the Measurement of 
Two-Phase Flow Parameters. MS Thesis, 
Oregon State University, US, 2001. 
[18]. T. Hibiki, M. Ishii, Z. Xiao., Axial interfacial 
area transport of vertical bubbly flows, 
International Journal of Heat and Mass 
Transfer (44) 1869–1888, 2001.