Evaluation of slip ratio correlations in two-phase flow

epends on the phase velocity ratio, 
slip ratio in the general form [8], [9] as a 
function of quality (x), density (ρ), and 
viscosity (µ): 
 (
 )
(
)
(
)
In reality, only several types of 
reactors for gas/liquid exist. Moreover, one 
could be noted that the contribution of the 
viscosity component as shown in Table I, 
(
)
, is less dominant. Therefore, this 
parameter could be negligible in the void 
fraction form. Void fraction correlations then 
could be reduced as follows: 
 (
)
(
)
 or 
 (
 ) (
)
Where the slip ratio, s, is determined 
as follows: 
 (
)
(
)
Select the void fraction correlations 
having the form in Eq. (7), the author has 
compared them with the available experimental 
data (Table I). 
Void fraction correlations related to slip 
ratio are listed in Table II. 
Where: Re and We are Reynolds and 
Weber numbers, D is the equivalent diameter. 
APRM, APA and M parameters are determined as 
followings: 
 {
 }, 
 (
)
, 
, (
)
(
)
, 
, 
, a 
 1+log(
) log(
) , 
 , σ is surface 
tension. 
Table I. References related void fraction data measurement. 
Reference Diameter[mm] Working fluid Geometry Pressure [psi] 
Marchettere[11] 127 Steam-Water Rectangular, vertical 114 - 600 
Cook [12] 127 Steam-Water Rectangular, vertical 114 - 600 
Haywood [13] 12.7-38.1 Steam-Water Pipe, horizontal 250 - 2100 
THANH TRAM TRAN, HYUN-SIK PARK
25 
Table II. Void fraction correlations. 
Correlation A b c d 
HEM [14] 1 1 1 0 
Fauske [15] 1 1 0.5 0 
Zivi [16] 1 1 0.67 0 
Smith [7] √
 (
 )
 1 1 0 
Chisholm [17] √ ( 
 ⁄ ) 
1 1 0 
Spendding & Chen [10] 2.22 0.65 0.65 0 
Hamersma & Hart [18] 0.26 0.67 0.33 0 
Tuner & Wallis [19] 1 0.72 0.4 0.08 
Lockhart & Martinelli [20] 0.28 0.64 0.36 0.07 
Thom [21] 1 1 0.89 0.18 
Baroczy [22] 1 0.74 0.65 0.13 
Premoli [23] APRM 1 1 0 
Madsen [24] 1 M -0.5 0 
Chen [25] 0.18 0.6 0.33 0.07 
Petalaz & Aziz [26] APA -0.2 -0.126 0 
Table III. Slip ratio correlations. 
Kim [6] has currently suggested that the 
slip ratio is the main parameter that could affect 
the diameter effect. In the past, some experimental 
work showed that critical mass flow rate increased 
while reducing the diameter of the throat (Sozzi 
and Sutherland [27], Chun and Park [28], Henry 
[29], Fauske [15]). The increase in the flow rate 
could be explained mainly based on the diameter 
effect. The raise of vaporization may be higher at 
the choking place with a decrease in sub-cooling 
upstream conditions at a very low sub-cooling 
temperature nozzle. It means that the slip ratio 
may increase for low sub-cooling upstream 
conditions. Several correlations of slip ratio were 
reviewed before taking them into account their 
critical flow predictions. 
Correlation Slip ratio, s 
HEM [14] 1 
Fauske [15] 
(
)
Zivi [16] 
(
)
Smith [7] 
 √
 (
 )
Spedding & Chen [10] 
2.22(
)
(
)
Hamersma & Hart [18] 
0.26(
)
(
)
EVALUATION OF SLIP RATIO CORRELATIONS IN TWO-PHASE FLOW 
26 
By comparing with the experimental 
data, void fraction correlations listed in Table I 
are evaluated. The six selected correlations are 
rewritten in the slip ratio form, as shown in 
Table III. Those slip ratio correlations will be 
evaluated in more detail using different 
pressures for both horizontal [11] and vertical 
[12],[13] tests. 
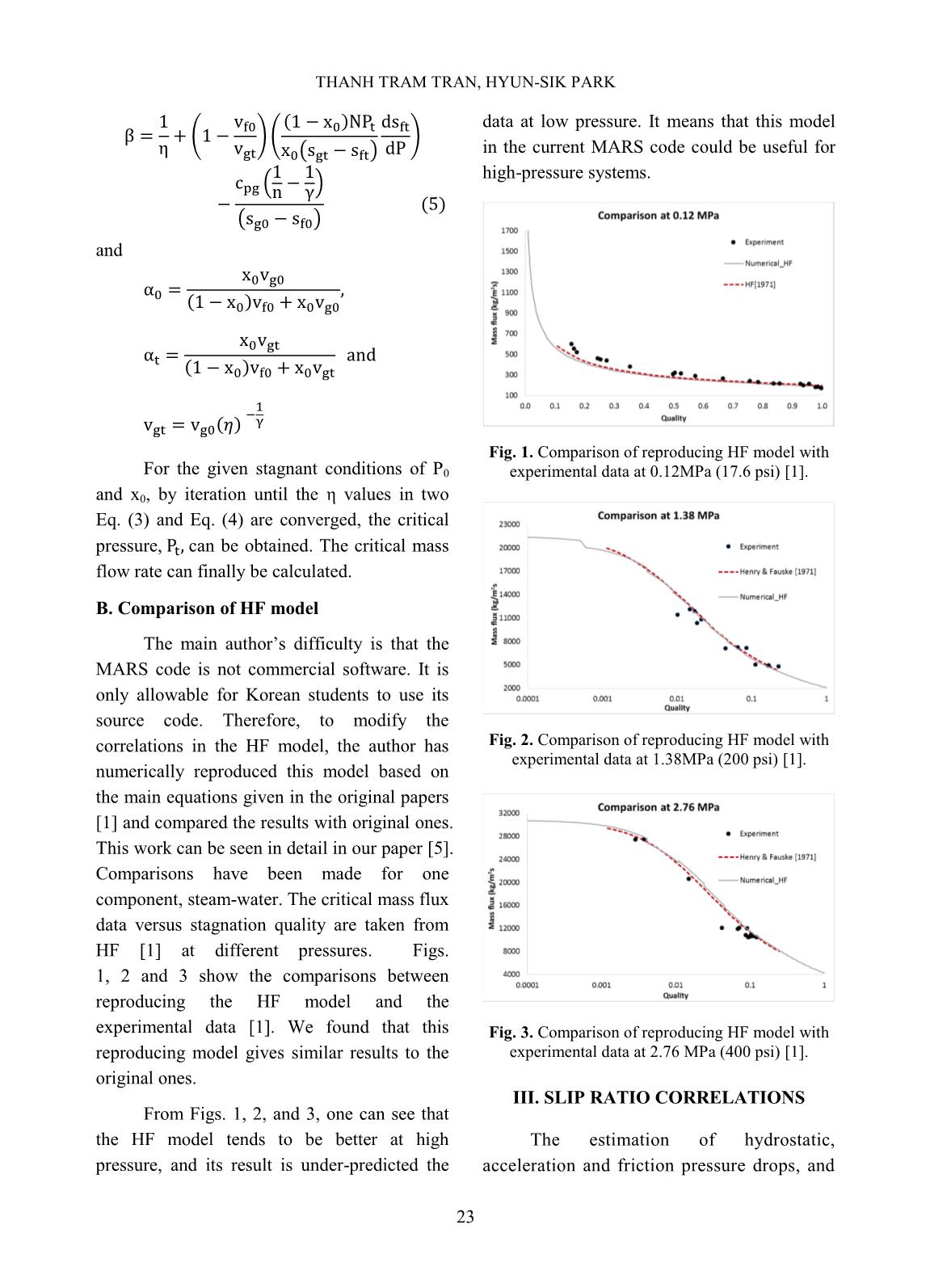
A. Evaluations using horizontal test data 
Chosen correlations are compared with 
Haywood data for a horizontal test in a high-
pressure range from 1.72 to 14.5 MPa, as 
shown in Figs. 4, 5, and 6. 
Even data changes in a high-pressure 
range, the original Smith’s correlation remains 
the best candidate. We can conclude that 
Smith’s correlation with his recommended k = 
0.4 gives the best predictions. 
Fig. 4. Void fraction vs. quality in comparing with 
the Haywood data at 4.14 MPa (600 psi) [13]. 
Fig. 5. Void fraction vs. quality in comparing with 
the Haywood data at 8.62 MPa (1250 psi) [13]. 
Fig. 6. Void fraction vs. quality in comparing with 
the Haywood data at 14.48 MPa (2100 psi) [13]. 
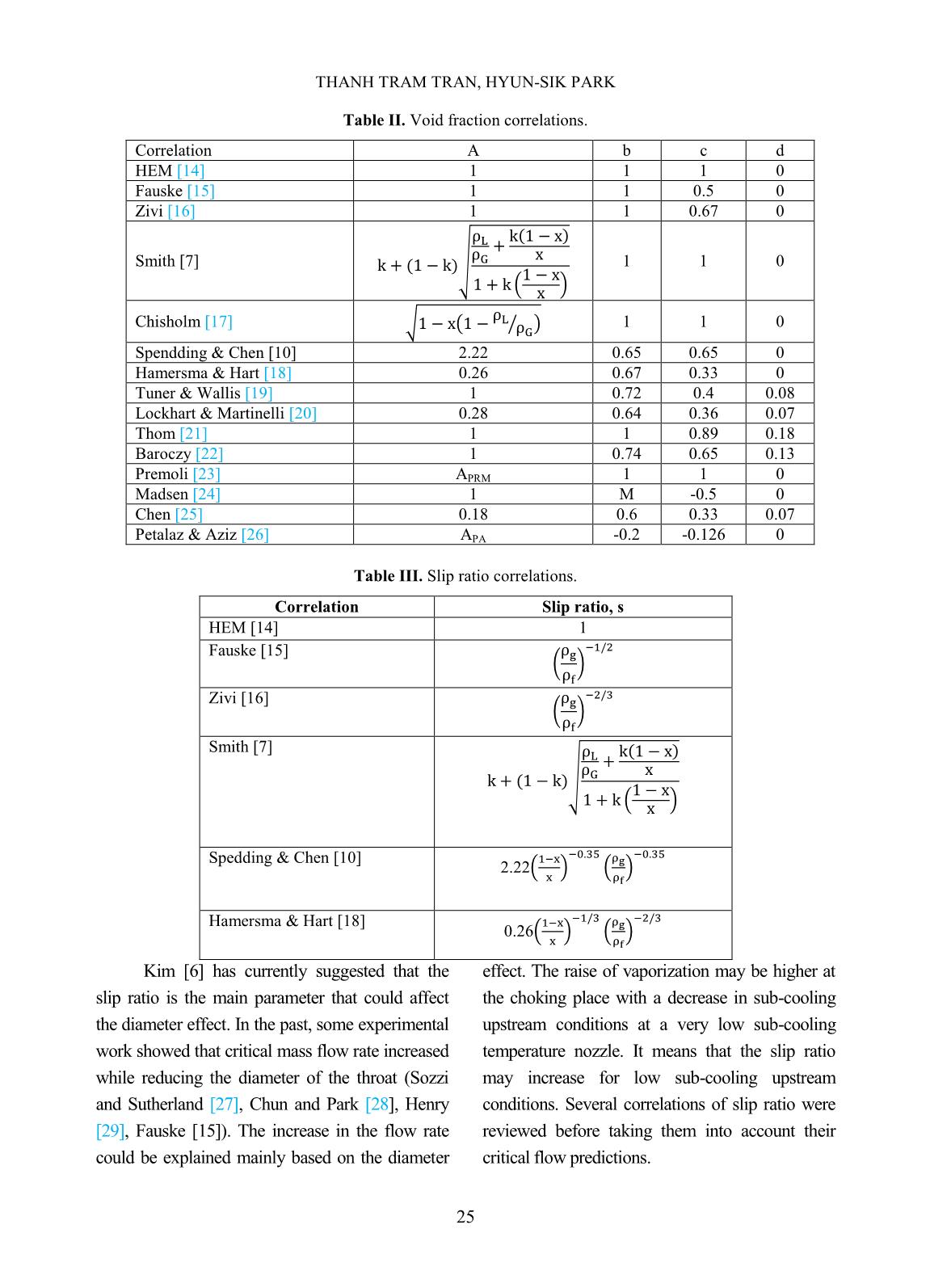
B. Evaluations using vertical test data 
Marchettere [11] and Cook [12] 
performed experiments using the same vertical 
test facility, but at different pressures varied 
from 0.69 to 4.14 MPa. The predictions of 
chosen correlations are compared with the 
vertical test data, as shown in Figs. 7, 8, and 9: 
Fig. 7. Void fraction vs. quality in comparing with 
the experimental data at 0.79 MPa (114.5 psi) [11]. 
Fig. 8. Void fraction vs. quality in comparing with 
the Experimental data at 1.89 MPa (274.3 psi) [11]. 
THANH TRAM TRAN, HYUN-SIK PARK
27 
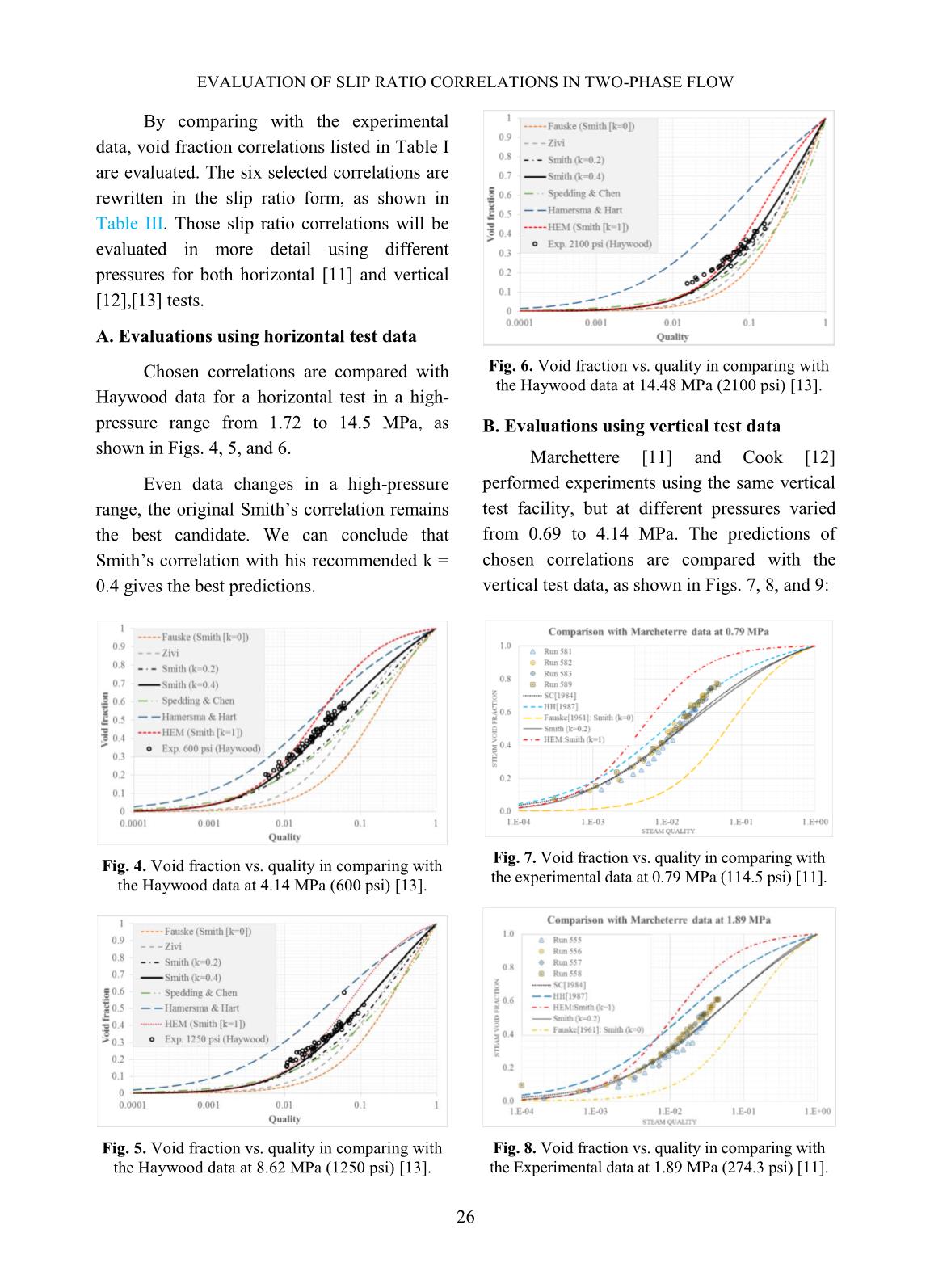
The comparison of predictions between 
the chosen correlations and the experimental 
data from Marchettere [11] and Cook [12] 
show that the modified Smith’s correlation 
with k = 0.2, as well as Speeding and Chen 
[10] one, are the best predictions. 
Fig. 9. Void fraction vs. quality in comparing with 
the experimental data at 4.24 MPa (614.4 psi) [12]. 
From these above comparisons, we 
could conclude that while the original Smith 
correlation with k=0.4 seems to be the best 
correlation for the horizontal test, its 
modification with k=0.2 could be the best 
correlation for the vertical test. 
IV. EVALUATION OF SMITH’S 
CORRELATION 
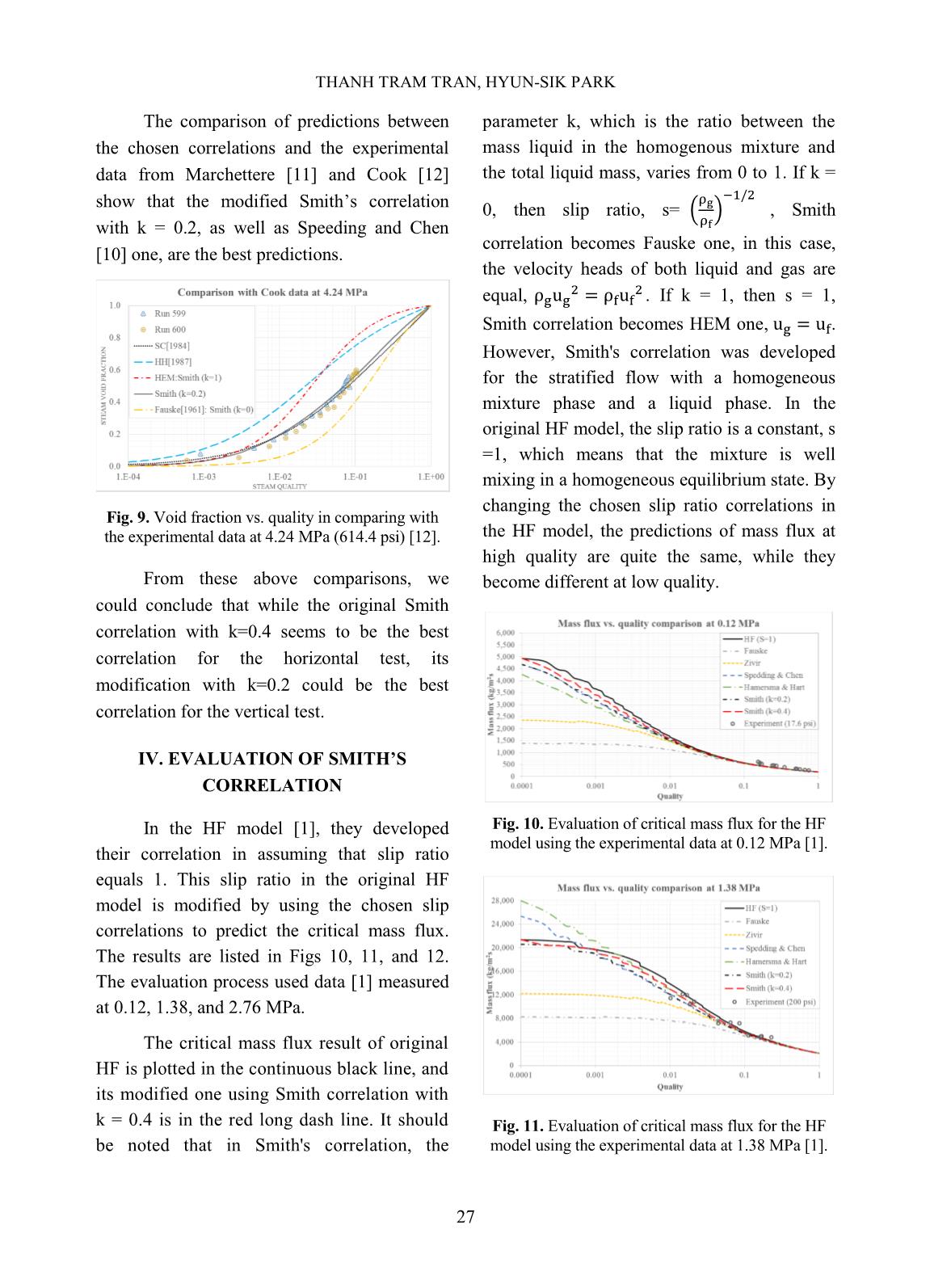
In the HF model [1], they developed 
their correlation in assuming that slip ratio 
equals 1. This slip ratio in the original HF 
model is modified by using the chosen slip 
correlations to predict the critical mass flux. 
The results are listed in Figs 10, 11, and 12. 
The evaluation process used data [1] measured 
at 0.12, 1.38, and 2.76 MPa. 
The critical mass flux result of original 
HF is plotted in the continuous black line, and 
its modified one using Smith correlation with 
k = 0.4 is in the red long dash line. It should 
be noted that in Smith's correlation, the 
parameter k, which is the ratio between the 
mass liquid in the homogenous mixture and 
the total liquid mass, varies from 0 to 1. If k = 
0, then slip ratio, s= (
)
 , Smith 
correlation becomes Fauske one, in this case, 
the velocity heads of both liquid and gas are 
equal, 
 . If k = 1, then s = 1, 
Smith correlation becomes HEM one, . 
However, Smith's correlation was developed 
for the stratified flow with a homogeneous 
mixture phase and a liquid phase. In the 
original HF model, the slip ratio is a constant, s 
=1, which means that the mixture is well 
mixing in a homogeneous equilibrium state. By 
changing the chosen slip ratio correlations in 
the HF model, the predictions of mass flux at 
high quality are quite the same, while they 
become different at low quality. 
Fig. 10. Evaluation of critical mass flux for the HF 
model using the experimental data at 0.12 MPa [1]. 
Fig. 11. Evaluation of critical mass flux for the HF 
model using the experimental data at 1.38 MPa [1]. 
EVALUATION OF SLIP RATIO CORRELATIONS IN TWO-PHASE FLOW 
28 
Fig. 12. Evaluation of critical mass flux for the HF 
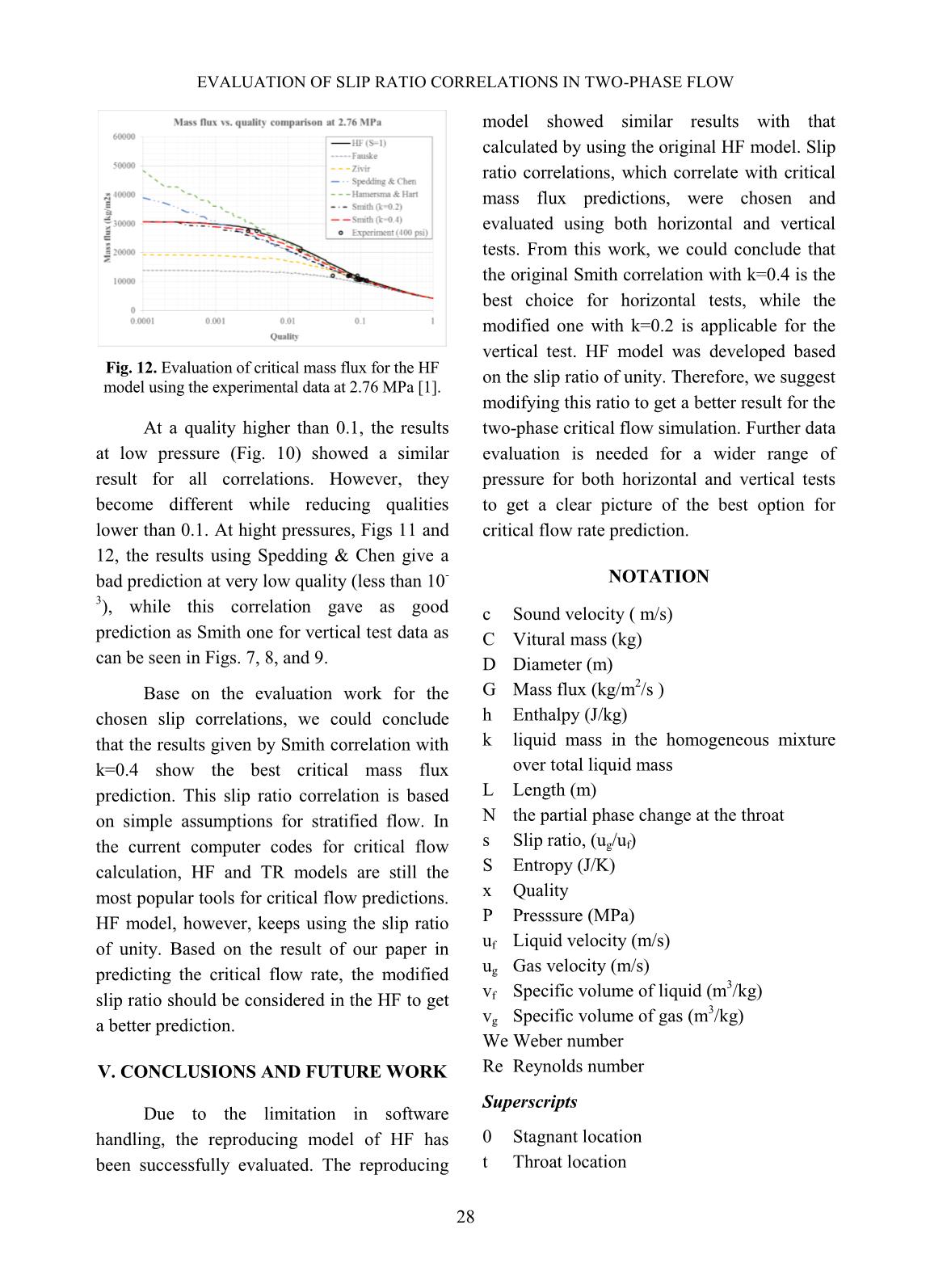
model using the experimental data at 2.76 MPa [1]. 
At a quality higher than 0.1, the results 
at low pressure (Fig. 10) showed a similar 
result for all correlations. However, they 
become different while reducing qualities 
lower than 0.1. At hight pressures, Figs 11 and 
12, the results using Spedding & Chen give a 
bad prediction at very low quality (less than 10
-
3
), while this correlation gave as good 
prediction as Smith one for vertical test data as 
can be seen in Figs. 7, 8, and 9. 
Base on the evaluation work for the 
chosen slip correlations, we could conclude 
that the results given by Smith correlation with 
k=0.4 show the best critical mass flux 
prediction. This slip ratio correlation is based 
on simple assumptions for stratified flow. In 
the current computer codes for critical flow 
calculation, HF and TR models are still the 
most popular tools for critical flow predictions. 
HF model, however, keeps using the slip ratio 
of unity. Based on the result of our paper in 
predicting the critical flow rate, the modified 
slip ratio should be considered in the HF to get 
a better prediction. 
V. CONCLUSIONS AND FUTURE WORK 
Due to the limitation in software 
handling, the reproducing model of HF has 
been successfully evaluated. The reproducing 
model showed similar results with that 
calculated by using the original HF model. Slip 
ratio correlations, which correlate with critical 
mass flux predictions, were chosen and 
evaluated using both horizontal and vertical 
tests. From this work, we could conclude that 
the original Smith correlation with k=0.4 is the 
best choice for horizontal tests, while the 
modified one with k=0.2 is applicable for the 
vertical test. HF model was developed based 
on the slip ratio of unity. Therefore, we suggest 
modifying this ratio to get a better result for the 
two-phase critical flow simulation. Further data 
evaluation is needed for a wider range of 
pressure for both horizontal and vertical tests 
to get a clear picture of the best option for 
critical flow rate prediction. 
NOTATION 
c Sound velocity ( m/s) 
C Vitural mass (kg) 
D Diameter (m) 
G Mass flux (kg/m
2
/s ) 
h Enthalpy (J/kg) 
k liquid mass in the homogeneous mixture 
over total liquid mass 
L Length (m) 
N the partial phase change at the throat 
s Slip ratio, (ug/uf) 
S Entropy (J/K) 
x Quality 
P Presssure (MPa) 
uf Liquid velocity (m/s) 
ug Gas velocity (m/s) 
vf Specific volume of liquid (m
3
/kg) 
vg Specific volume of gas (m
3
/kg) 
We Weber number 
Re Reynolds number 
Superscripts 
0 Stagnant location 
t Throat location 
THANH TRAM TRAN, HYUN-SIK PARK
29 
g Gas component 
f Fluid component 
Greeks 
α Void fraction 
γ Isentropic exponent 
λ The root of characteristic equation 
η Critical pressure ratio 
ρf Liquid density (kg/m
3
) 
ρg Gas density (kg/m
3
) 
µf Liquid viscosity (Ns/m
2
) 
µg Gas viscosity (Ns/m
2
) 
REFERENCE 
[1]. R. E. Henry, H. K. Fauske, “The two-phase 
critical flow of one-component mixtures in 
nozzles, orifices and short tubes”, Journal of 
heat transfer, 93, 179-187, 1971. 
[2]. J. A. Trap and V. H. Ransom, “A choked-flow 
calculation criterion for nonhomogeneous, 
nonequilibrium, two-phase flows”, Int. J. 
Multiphase Flow, 8, 669-681, 1982. 
[3]. B. D. Chung et al., MARS Code Manual 
Volume V: Models and Correlations, 
KAERI, 2006. 
[4]. TRACE, V5.0, Theory manual, Field 
Equations, solution methods, and physical 
models, 2010. 
[5]. T. T. Tran, Y.S. Kim, H.S. Park, Study on the 
most applicable critical flow models in the 
current system codes, KNS Conference 
2017, Korea. 
[6]. Y. S. Kim et al., “Overview of geometrical 
effects on the critical flow rate of sub-cooled 
and saturated water”, Annals of Nuclear 
Energy, 76, 12-18, 2015. 
[7]. S. L. Smith, “Void fractions in two-phase flow: 
a correlation based upon an equal velocity 
head model”, Proc. Inst. Mech. Engrs, 184, 
647-657, Part 1, 1969. 
[8]. D. Butterworth, “A comparison of some void 
fraction relationships for co-current gas-liquid 
flow”, Int. J. Multiphase Flow, 1, 845-850, 1975. 
[9]. M.A. Woldesemayat, A.J. Ghajar, “Comparison 
of void fraction correlations for different flow 
patterns in horizontal and upward vertical 
pipes”, International Journal of Multiphase 
Flow, 33, 347–370, 2007. 
[10]. P. L. Spedding, J. J. J. Chen, “Holdup in two-
phase flow”, Int. J. Multiphase Flow, 10, 307-
339, 1984. 
[11]. Marchettere, The effect of pressure on boiling 
density in multiple rectangular channels, 
Argonne National Laboratory, Illinois, United 
States, 1956. 
[12]. Cook, Boiling density in vertical rectangular 
multichannel sections with natural circulation, 
Argonne National Laboratory, Illinois, United 
States, 1956. 
[13]. Haywood, Experimental study on the flow 
conditions and pressure drop of steam-
water mixture at high pressure in heated 
and unheated tubes, University of 
Cambridge, 1961. 
[14]. E. S. Starkman et al., “Expansion of a very 
low-quality two-phase fluid through a 
convergent-divergent nozzle”, Journal of Basic 
Engineering, 86, 247-254, 1964. 
[15]. H. K. Fauske, Contribution to the theory of 
two-phase, one-component critical flow, 
Argonne National Lab, United States, 1962. 
[16]. S.M. Zivi, “Estimation of steady-state steam 
void fraction by means of the principle of 
minimum entropy production”. Trans. ASME, 
J. Heat Transfer, 86, 247–252, 1964. 
[17]. D. Chisholm, “Pressure gradients due to 
friction during the flow of evaporating two-
phase mixtures in smooth tubes and channels”, 
Int. J. Heat Mass Transfer, 16, 347-358, 1973. 
[18]. P.J. Hamersma, J. Hart,. “A pressure drop 
correlation for gas/liquid pipe flow with a 
small liquid holdup”. Chem. Eng. Sci. 
42,1187–1196, 1987. 
[19]. J.M. Turner, G.B. Wallis, The separate-
cylinders model of two-phase flow, Paper No. 
NYO-3114-6, Thayer’s School Eng., 
Dartmouth College, Hanover, NH, USA, 1965. 
EVALUATION OF SLIP RATIO CORRELATIONS IN TWO-PHASE FLOW 
30 
[20]. R.W. Lockhart, R.C. Martinelli, “Proposed 
correlation of data for isothermal two-phase, 
two-component flow in pipes”, Chem. Eng. 
Progr. 45, 39–48, 1949. 
[21]. J.R.S. Thom, “Prediction of pressure drop 
during forced circulation boiling of water”, Int. 
J. Heat Mass Transfer 7, 709–724, 1964. 
[22]. C.J. Baroczy, “A systemic correlation for two-
phase pressure drop”, Chem. Eng. Progr. 
Symp. Ser. 62, 232–249, 1966. 
[23]. A. Premoli, D. Francesco, A. Prima, An 
empirical correlation for evaluating two-phase 
mixture density under adiabatic conditions, 
European Two-Phase Flow Group Meeting, 
Milan, Italy, 1970. 
[24]. N. Madsen, “A void fraction correlation for 
vertical and horizontal bulk-boiling of water”. 
AIChE J. 21, 607–608, 1975. 
[25]. J.J.J. Chen, “A further examination of void-
fraction in the annular two-phase flow”, Int. J. 
Heat Mass Transfer 29, 1760–1763, 1986. 
[26]. N. Petalaz, K. Aziz, A mechanistic model for 
stabilized multiphase flow in pipes, a report for 
the members of Stanford reservoir simulation 
industrial affiliates and Stanford project on the 
productivity and injectivity of horizontal wells, 
Stanford University, Palo Alto, CA, 1997. 
[27]. G. L. Sozzi, W. A. Sutherland, “Critical flow 
of saturated and subcooled water at high 
pressure”, Amer. Soc. Mech. Eng. Non-
Equilibrium Two-Phase Flow Symp., 47, 1975. 
[28]. M. H. Chun and C. K. Park, “An experimental 
investigation of critical flow rates of subcooled 
water through short pipes with small 
diameters”, Int. Comm. Heat Mass Transfer, 23 
(No. 8), 1053-1064, 1996. 
[29]. R. E. Henry, Pressure pulse propagation in 
two-phase one and two-component mixtures, 
ANL-7792, Argonne National Laboratory. 
Illinois, United States, 1971.