Evaluating uncertainty of some radiation measurand using Monte Carlo method

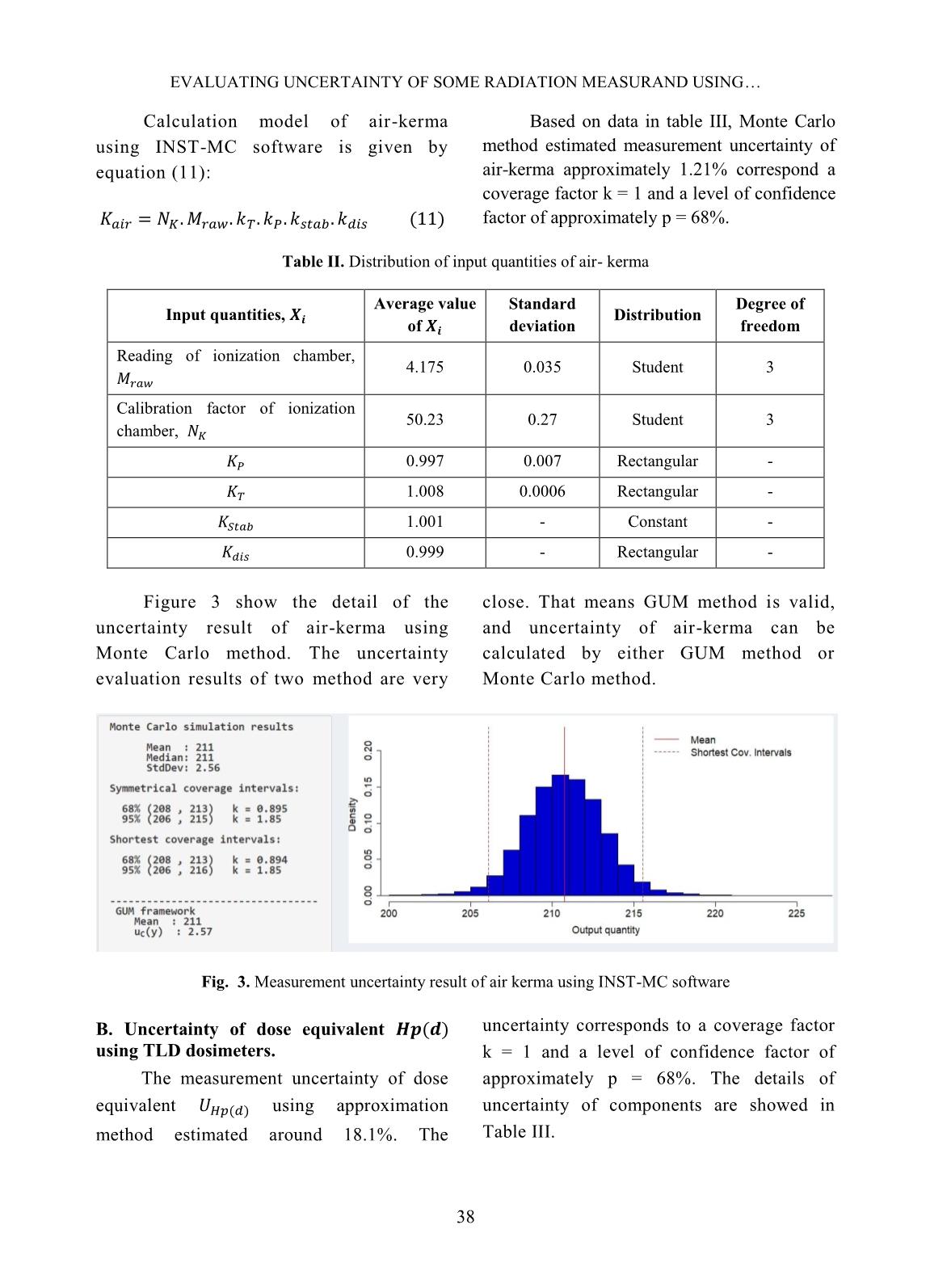
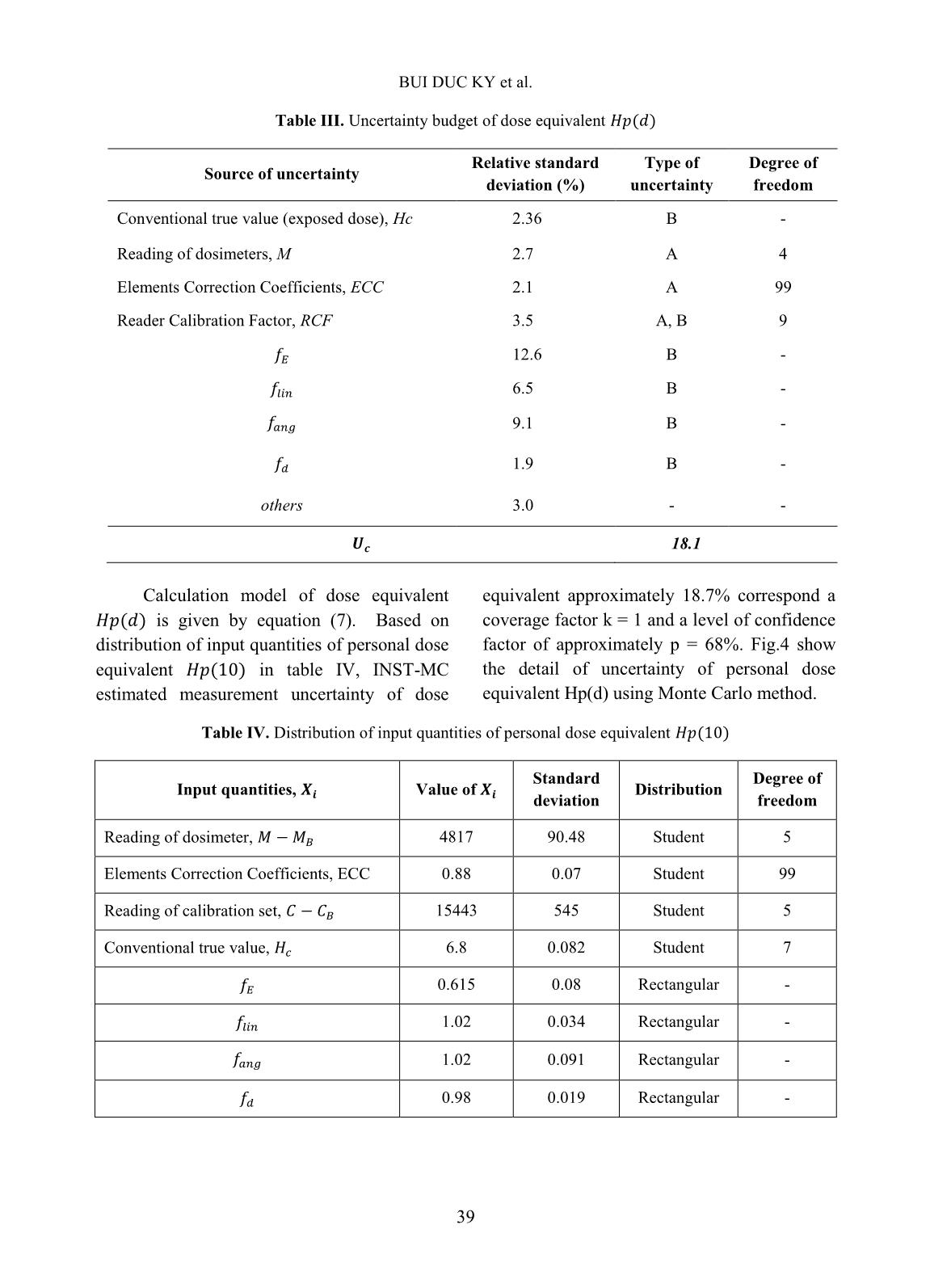
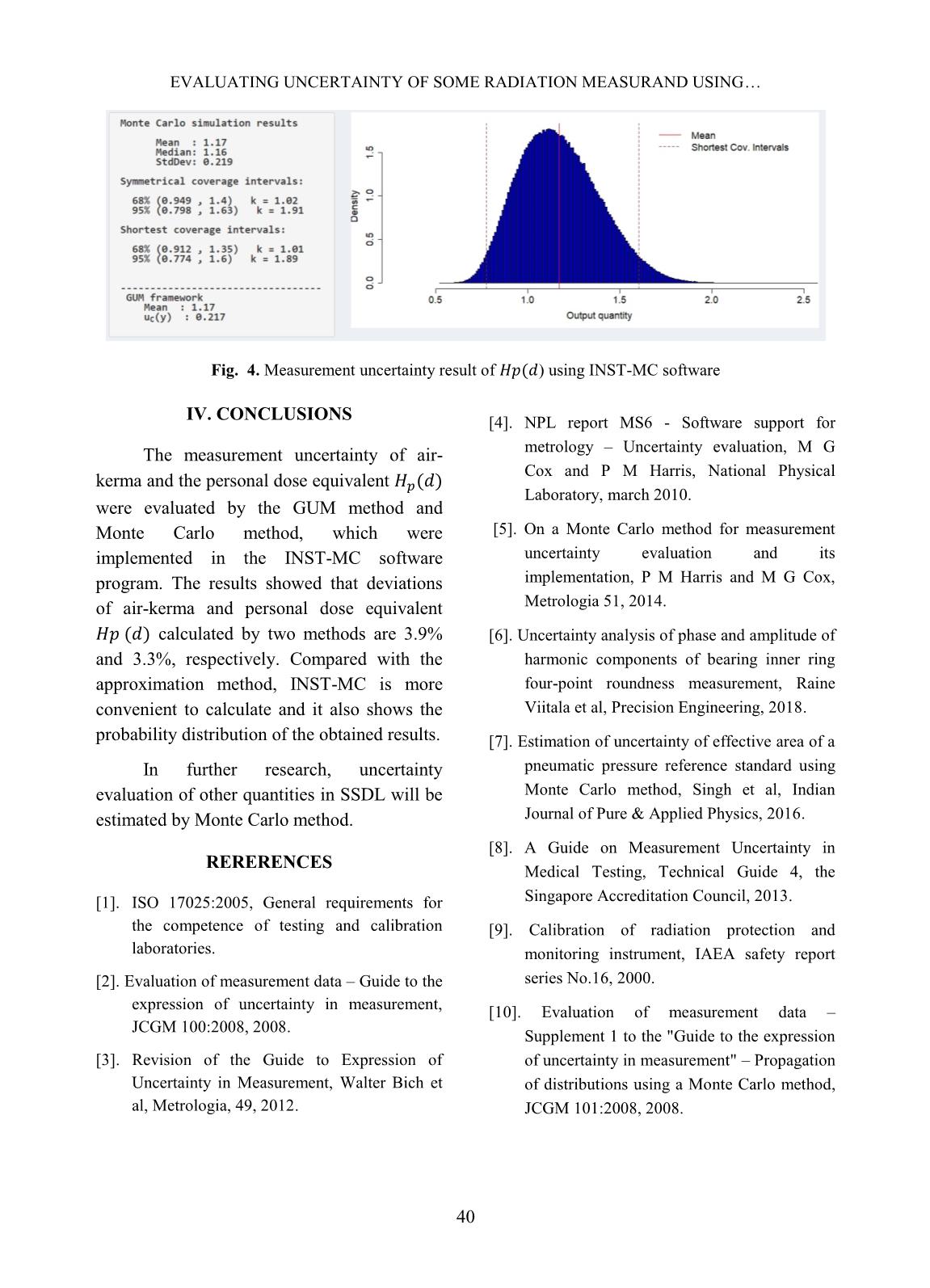
Nuclear Science and Technology, Vol.9, No. 4 (2019), pp. 34-40 
©2019 Vietnam Atomic Energy Society and Vietnam Atomic Energy Institute 
Evaluating uncertainty of some radiation measurand using 
Monte Carlo method 
Bui Duc Ky
*
, Nguyen Ngoc Quynh, Duong Duc Thang, Le Ngoc Thiem, Ho Quang Tuan, 
Tran Thanh Ha, Bui Thi Anh Duong, Nguyen Huu Quyet, Duong Van Trieu 
Institute for Nuclear Science and Technology, Hanoi, Vietnam 
Email: Duckyb2@gmail.com 
(Received 07 November 2019, accepted 26 December 2019) 
Abstract: Evaluating measurement uncertainty of a physical quantity is a mandatory requirement for 
laboratories within the recognition ISO/IEC 17025 certification to access reliability of measured 
results. In this work, the uncertainty of ionizing radiation measurements such as air-kerma, personal 
dose equivalent was evaluated based on GUM method and Monte Carlo method. An 
uncertainty propagation software has been developed for evaluation of the measurement uncertainty 
more convenient. 
Key words: Uncertainty measurement, Monte Carlo method. 
I. INTRODUCTION 
The measurement uncertainty is a 
characteristic for the dispersion of measurable 
values of a quantity to be measured [1, 2, 3]. 
Because without the measurement uncertainty, 
the results of the measurements cannot be 
compared to each other, nor can be compared 
to conventional true values. 
In the field of measurement of ionizing 
radiation ISO/IEC and IAEA has provided 
guidance on measurement uncertainty for 
different measurement quantities. These 
documents are primarily based on the 
evaluation methods provided by the 
International Commission on Measurement 
Guidelines (JCGM). The uncertainty 
propagation method described in the JCGM 
100:2008 “Guide to the expression of 
uncertainty in measurement” is often referred 
to as the GUM method. The Monte Carlo 
method was described in its supplement 1 
“Guide to the expression of uncertainty in 
measurement – Propagation of distributions 
using a Monte Carlo method”. 
In this work, uncertainty of air-kerma 
and personal dose equivalent 
quantities were evaluated by both methods. 
These two quantities are the fundamental 
quantities in radiation protection field. All 
experimental data published in this work 
were measured at the Secondary Standard 
Dosimetry Laboratory belongs to Institute for 
Nuclear Science and Technology. 
II. METHODS 
The relationship between a single real 
output quantity y and a number of real input 
quantities has the following equation (1). 
A. GUM method 
Uncertainty of the input quantities 
are divided into two categories, based on how 
its values were evaluated. If it was evaluated 
based on statistical means, they are called type 
A. Otherwise, they are nominated type B. 
However, it is worth mentioning that this 
classification does not affect the uncertainty 
propagation law. 
BUI DUC KY et al. 
35 
The uncertainty of output quantity Y is 
calculated as [2, 3, 4]: 
 ∑ 
 ∑ ∑ 
 ( ) 
Where, and are 
sensitivity coefficients, is the 
estimated covariance associated with and . 
 The GUM uncertainty framework 
requires [4]: 
a) The non-linearity of the measurement 
function to be insignificant. 
b) The central limit theorem to apply, 
implying the representativeness of the 
Probability density function (PDF) for the 
output quantity by a Gaussian distribution or a 
t-distribution. 
c) The adequacy of the Welch-
Satterthwaite formula for calculating the 
effective degrees of freedom. 
 In practice, the GUM method is 
frequently used in violation of the requirements 
listed above or without knowing whether these 
requirements hold (with an unquantified degree 
of approximation). Furthermore, the equation 2 
is only the first order Taylor series 
approximation. This makes calculated 
uncertainty in many cases inaccurate. 
B. Monte Carlo method 
 The Monte Carlo method simulates input 
quantities based on initial probability 
distribution. The distribution of the input 
quantities will affect the output quantity 
according to the model in the equation 1. As 
result, the distribution function of the output 
quantity was obtained. Therefore, not only the 
standard deviation but other characteristics of 
output quantity can be determined (i.e. 
skewness, coverage interval). The process of 
uncertainty evaluation using Monte Carlo 
method was presented in fig.1 [2, 4]. 
 The advantages of the Monte Carlo 
method are that it doesn’t make any 
assumption about linearity of measurement 
function nor PDF of the output quantity. 
Therefore, the Monte Carlo method is valid for 
wider range of problem compare to GUM 
method. Its result can be used to validate the 
result of GUM method. 
 The disadvantage of the Monte Carlo 
method is that it is impossible using hand 
calculation. This method must be implemented 
in a computer software. 
Fig. 1. Uncertainty measurement using a Monte Carlo method for a univariate, real measurement function.[4] 
EVALUATING UNCERTAINTY OF SOME RADIATION MEASURAND USING 
36 
C. INST-MC software 
 A software program, namely INST-MC 
was developed to facilitate the uncertainty 
evaluation. The interface of the software is 
shown in fig.2. Both methods of uncertainty 
evaluation discussed above were 
implemented. In the first version of INST-
MC, most common distributions in radiation 
measurement are included: Gaussian 
distribution, t-distribution, Poisson 
distribution, uniform distribution, triangular 
distribution, etc. The program was validated 
by comparing with the NIST uncertainty 
machine, an uncertainty software has been 
developed by National Institute of Standard 
and Technology/ USA. 
Fig. 2. Interface of INST-MC uncertainty software. 
III. RADIATION MEASURAND 
A. Air-kerma of 
137
Cs source. 
The air-kerma is obtained from Eq.3 
Where: is calibration factor of 
ionization chamber, is correction factor of 
the difference between the reference beam 
quality, , and the actual quality, , during the 
measurement and is corrected reading of 
ionization chamber: 
 is reading of ionization chamber, 
 corrects for the deviation of the actual 
air temperature T from the reference 
temperature K, 
 corrects 
for the deviation of the actual air pressure P 
from the reference temperature 
 mbar, corrects for the unstable of 
ionization chamber, corrects for the 
possible deviation of the actual distance of the 
reference source to the measuring instrument 
from the nominal calibration distance. 
 Using the equation 2, uncertainty of air- 
kerma U(K) and corrected reading U(Mcorr) is 
given by: 
 √ 
√
(
)
 (
)
 (
)
 (
 ) 
 (
 )
INST-MC 
BUI DUC KY et al. 
37 
B. Personal dose equivalent using 
TLD dosimeter. 
Personal dose equivalent Hp(d) is 
obtained from equation (7): 
Where: M is reading of exposed dosimeter, 
is reading of background dosimeter. 
ECC is elements correction coefficients. 
 ̅
 ̅ is average reading of n dosimeters and is 
reading of i
th 
dosimeter (i= ̅̅ ̅̅ ̅̅ ̅ ). 
RCF is reader calibration factor: 
C is reading of calibration set, is reading of 
background calibration set, is conventional 
true value (exposed dose), corrects for 
energy dependence of dosimeter, corrects 
for non-linearity of dosimeter, corrects for 
the loss signal before reading dosimeter, 
corrects for the inhomogeneity response of 
dosimeter, corrects for others affect. 
The uncertainty of personal dose 
equivalent ) is obtained from equation 10. 
√
(
)
 (
)
(
)
 (
 ) 
(
)
 (
 ( )
 )
 (
)
IV. RESULTS AND DICUSSION 
A. Uncertainty of air-kerma with the 
gamma rays of 
137
Cs. 
 The measurement uncertainty of air-
kerma using approximation method 
estimated around 1.26%. The uncertainty 
corresponds to a coverage factor k = 1 and a 
level of confidence factor of approximately p = 
68%. The details of uncertainty of components 
showed in Table I. 
Table I. Uncertainty budget of air-kerma 
Source of uncertainty 
Relative standard 
deviation (%) 
Type of 
uncertainty 
Degree of 
freedom 
Calibration factor of ionization 
chamber 
0.41 B - 
Reading of ionization chamber 0.10 A 9 
Air pressure 0.11 B - 
Air temperature 0.10 B - 
Distance 0.13 B - 
Stability of ionization chamber 0.60 A, B - 
Others 1.00 A, B - 
 1.26 
EVALUATING UNCERTAINTY OF SOME RADIATION MEASURAND USING 
38 
Calculation model of air-kerma 
using INST-MC software is given by 
equation (11): 
Based on data in table III, Monte Carlo 
method estimated measurement uncertainty of 
air-kerma approximately 1.21% correspond a 
coverage factor k = 1 and a level of confidence 
factor of approximately p = 68%. 
Table II. Distribution of input quantities of air- kerma 
Input quantities, 
Average value 
of 
Standard 
deviation 
Distribution 
Degree of 
freedom 
Reading of ionization chamber, 
4.175 0.035 Student 3 
Calibration factor of ionization 
chamber, 
50.23 0.27 Student 3 
 0.997 0.007 Rectangular - 
 1.008 0.0006 Rectangular - 
 1.001 - Constant - 
 0.999 - Rectangular - 
Figure 3 show the detail of the 
uncertainty result of air-kerma using 
Monte Carlo method. The uncertainty 
evaluation results of two method are very 
close. That means GUM method is valid, 
and uncertainty of air-kerma can be 
calculated by either GUM method or 
Monte Carlo method. 
Fig. 3. Measurement uncertainty result of air kerma using INST-MC software 
B. Uncertainty of dose equivalent 
using TLD dosimeters. 
 The measurement uncertainty of dose 
equivalent using approximation 
method estimated around 18.1%. The 
uncertainty corresponds to a coverage factor 
k = 1 and a level of confidence factor of 
approximately p = 68%. The details of 
uncertainty of components are showed in 
Table III. 
BUI DUC KY et al. 
39 
Table III. Uncertainty budget of dose equivalent 
Source of uncertainty 
Relative standard 
deviation (%) 
Type of 
uncertainty 
Degree of 
freedom 
Conventional true value (exposed dose), Hc 2.36 B - 
Reading of dosimeters, M 2.7 A 4 
Elements Correction Coefficients, ECC 2.1 A 99 
Reader Calibration Factor, RCF 3.5 A, B 9 
 12.6 B - 
 6.5 B - 
 9.1 B - 
 1.9 B - 
others 3.0 - - 
 18.1 
Calculation model of dose equivalent 
 is given by equation (7). Based on 
distribution of input quantities of personal dose 
equivalent in table IV, INST-MC 
estimated measurement uncertainty of dose 
equivalent approximately 18.7% correspond a 
coverage factor k = 1 and a level of confidence 
factor of approximately p = 68%. Fig.4 show 
the detail of uncertainty of personal dose 
equivalent Hp(d) using Monte Carlo method. 
Table IV. Distribution of input quantities of personal dose equivalent 
Input quantities, Value of 
Standard 
deviation 
Distribution 
Degree of 
freedom 
Reading of dosimeter, 4817 90.48 Student 5 
Elements Correction Coefficients, ECC 0.88 0.07 Student 99 
Reading of calibration set, 15443 545 Student 5 
Conventional true value, 6.8 0.082 Student 7 
 0.615 0.08 Rectangular - 
 1.02 0.034 Rectangular - 
 1.02 0.091 Rectangular - 
 0.98 0.019 Rectangular - 
EVALUATING UNCERTAINTY OF SOME RADIATION MEASURAND USING 
40 
Fig. 4. Measurement uncertainty result of ) using INST-MC software 
IV. CONCLUSIONS 
The measurement uncertainty of air-
kerma and the personal dose equivalent 
were evaluated by the GUM method and 
Monte Carlo method, which were 
implemented in the INST-MC software 
program. The results showed that deviations 
of air-kerma and personal dose equivalent 
 calculated by two methods are 3.9% 
and 3.3%, respectively. Compared with the 
approximation method, INST-MC is more 
convenient to calculate and it also shows the 
probability distribution of the obtained results. 
In further research, uncertainty 
evaluation of other quantities in SSDL will be 
estimated by Monte Carlo method. 
RERERENCES 
[1]. ISO 17025:2005, General requirements for 
the competence of testing and calibration 
laboratories. 
[2]. Evaluation of measurement data – Guide to the 
expression of uncertainty in measurement, 
JCGM 100:2008, 2008. 
[3]. Revision of the Guide to Expression of 
Uncertainty in Measurement, Walter Bich et 
al, Metrologia, 49, 2012. 
[4]. NPL report MS6 - Software support for 
metrology – Uncertainty evaluation, M G 
Cox and P M Harris, National Physical 
Laboratory, march 2010. 
 [5]. On a Monte Carlo method for measurement 
uncertainty evaluation and its 
implementation, P M Harris and M G Cox, 
Metrologia 51, 2014. 
[6]. Uncertainty analysis of phase and amplitude of 
harmonic components of bearing inner ring 
four-point roundness measurement, Raine 
Viitala et al, Precision Engineering, 2018. 
[7]. Estimation of uncertainty of effective area of a 
pneumatic pressure reference standard using 
Monte Carlo method, Singh et al, Indian 
Journal of Pure & Applied Physics, 2016. 
[8]. A Guide on Measurement Uncertainty in 
Medical Testing, Technical Guide 4, the 
Singapore Accreditation Council, 2013. 
[9]. Calibration of radiation protection and 
monitoring instrument, IAEA safety report 
series No.16, 2000. 
[10]. Evaluation of measurement data – 
Supplement 1 to the "Guide to the expression 
of uncertainty in measurement" – Propagation 
of distributions using a Monte Carlo method, 
JCGM 101:2008, 2008.