Discussion on log - Based operators for real-time text detection

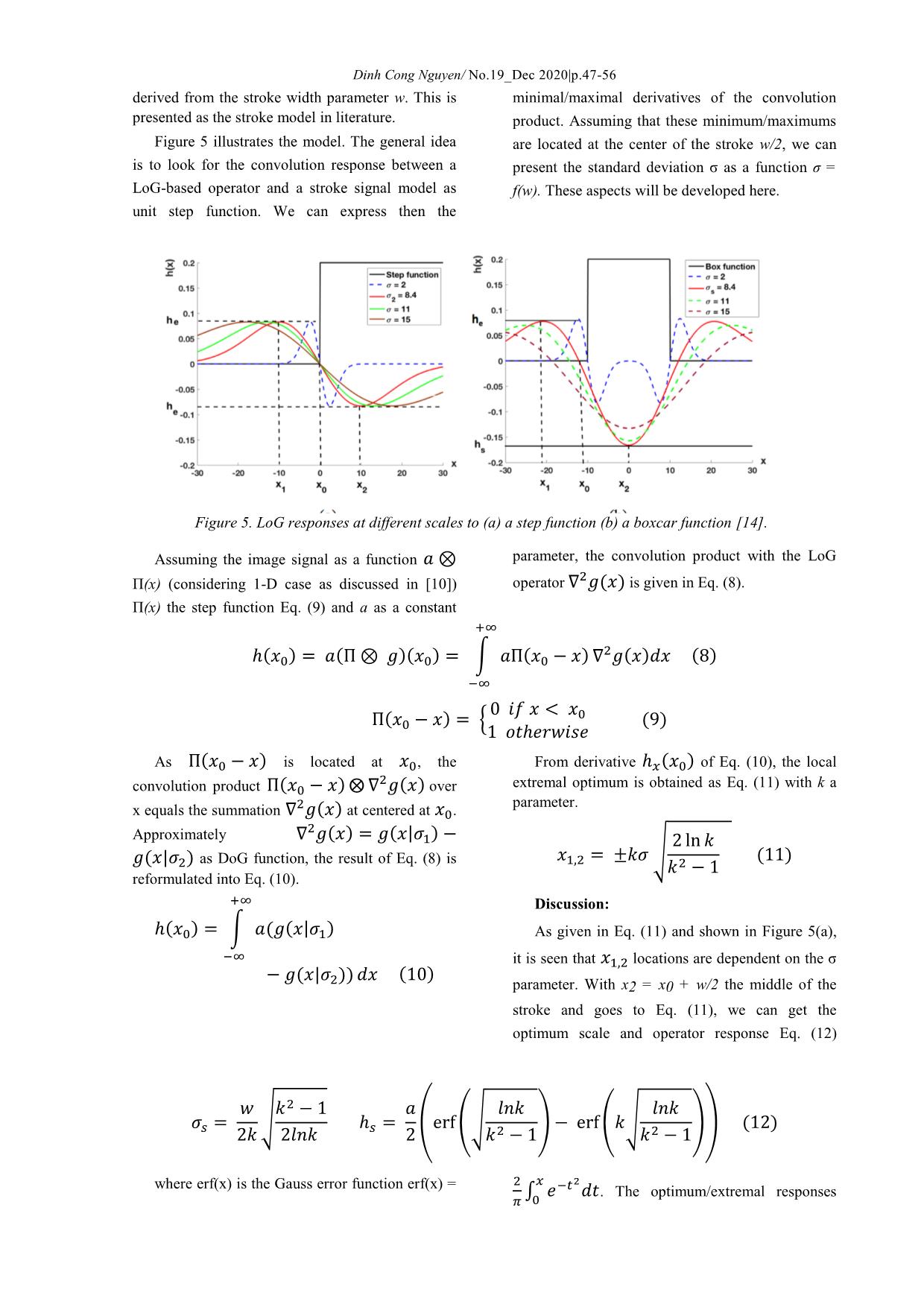
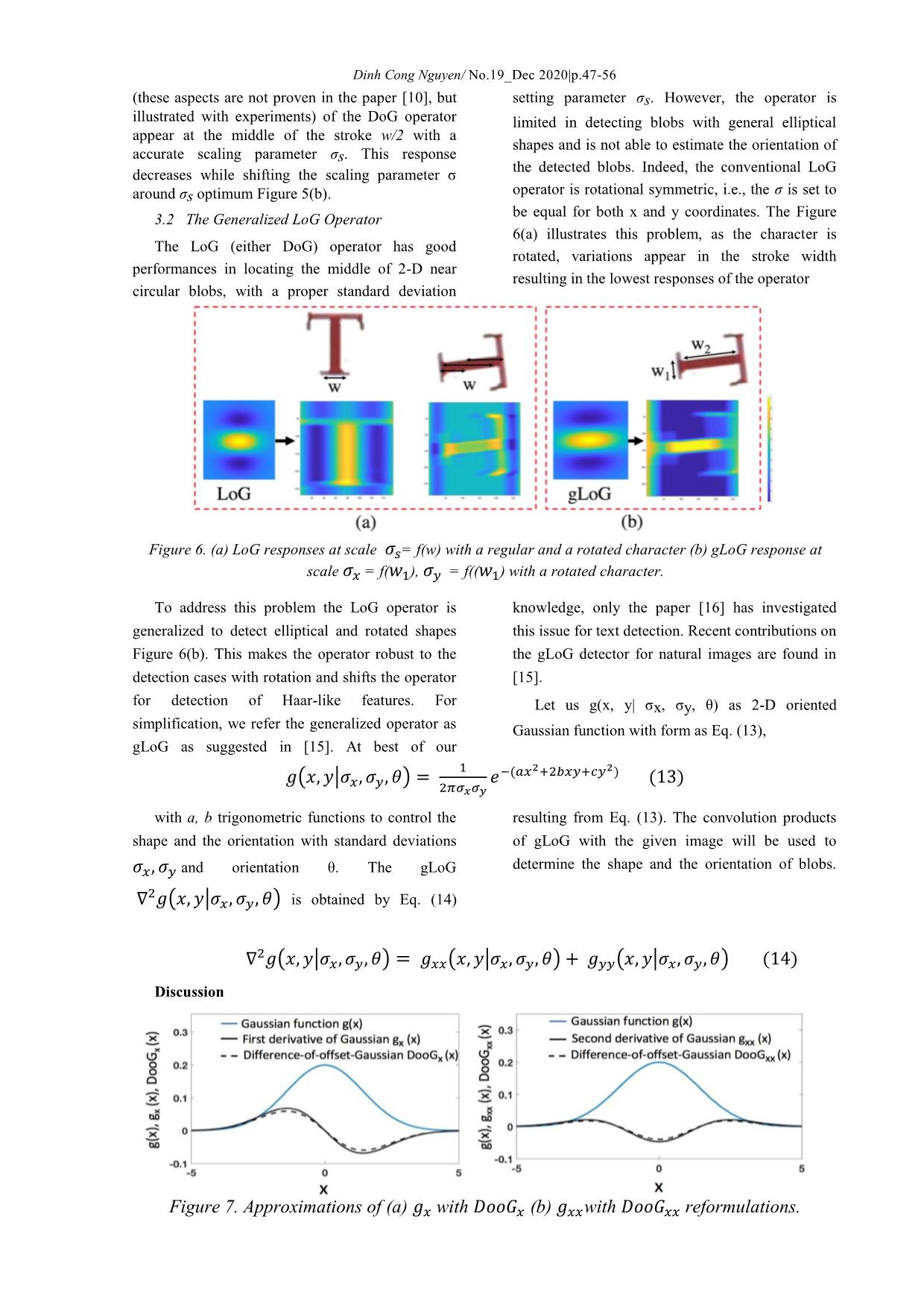
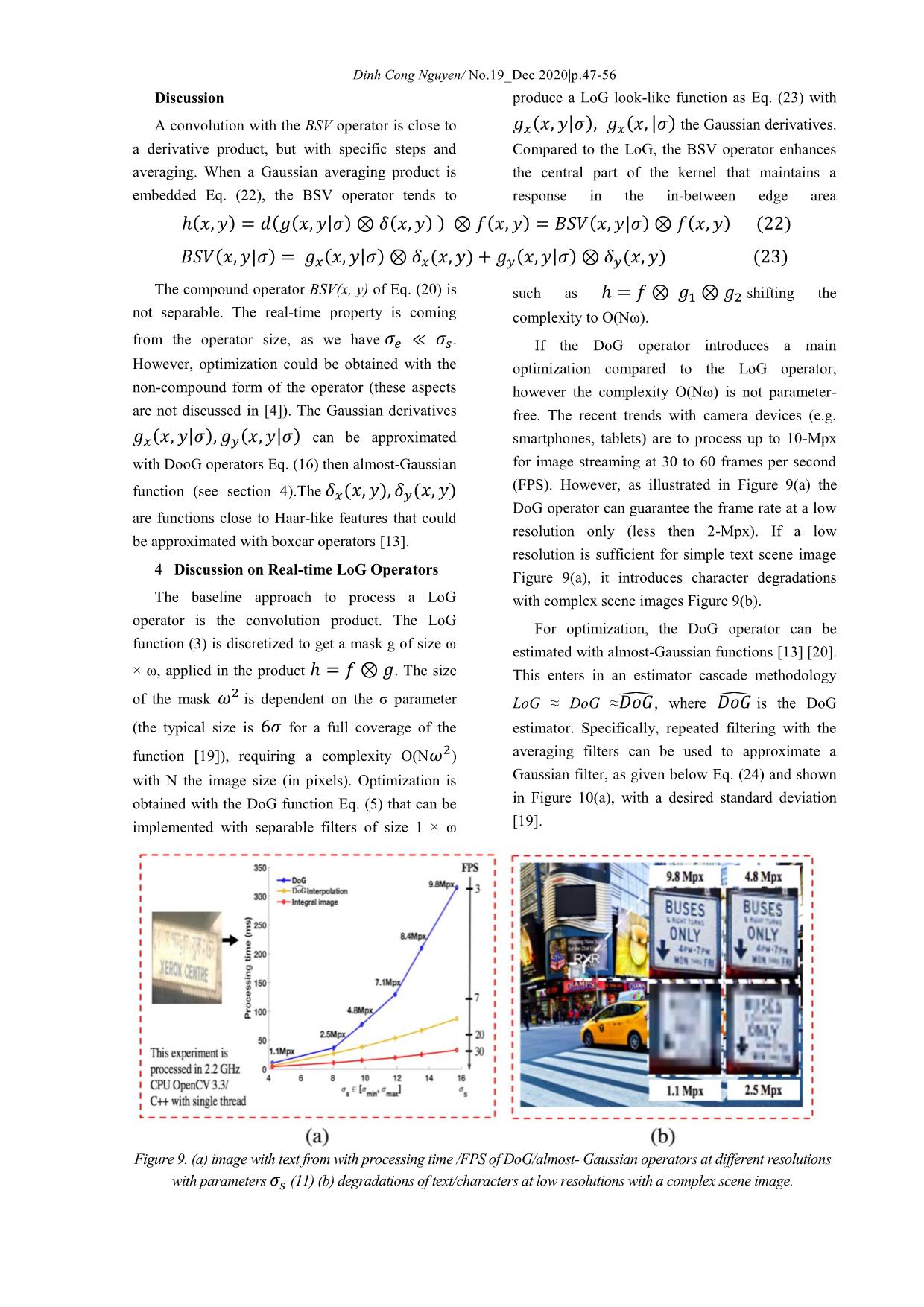
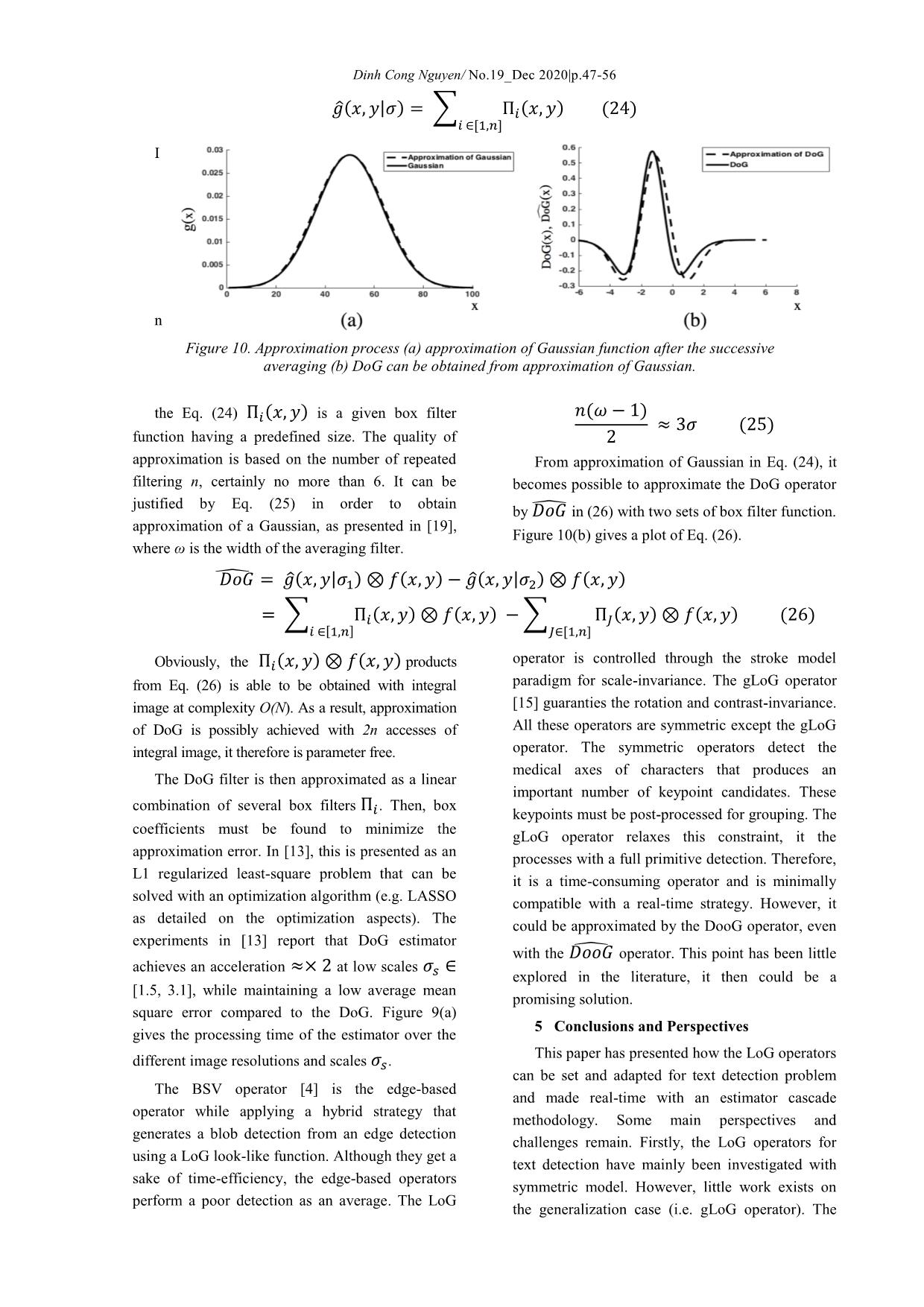
.47-56 
(these aspects are not proven in the paper [10], but setting parameter σs. However, the operator is 
illustrated with experiments) of the DoG operator limited in detecting blobs with general elliptical 
appear at the middle of the stroke w/2 with a 
 shapes and is not able to estimate the orientation of 
accurate scaling parameter σs. This response 
 the detected blobs. Indeed, the conventional LoG 
decreases while shifting the scaling parameter σ 
around σs optimum Figure 5(b). operator is rotational symmetric, i.e., the σ is set to 
 be equal for both x and y coordinates. The Figure 
 3.2 The Generalized LoG Operator 
 6(a) illustrates this problem, as the character is 
 The LoG (either DoG) operator has good 
 rotated, variations appear in the stroke width 
performances in locating the middle of 2-D near 
 resulting in the lowest responses of the operator 
circular blobs, with a proper standard deviation 
 Figure 6. (a) LoG responses at scale 휎푠= f(w) with a regular and a rotated character (b) gLoG response at 
 scale 휎 = f(푤 ), 휎 = f((푤 ) with a rotated character. 
 To address this problem the LoG operator is knowledge, only the paper [16] has investigated 
generalized to detect elliptical and rotated shapes this issue for text detection. Recent contributions on 
Figure 6(b). This makes the operator robust to the the gLoG detector for natural images are found in 
detection cases with rotation and shifts the operator [15]. 
for detection of Haar-like features. For Let us g(x, y| σx, σy, θ) as 2-D oriented 
simplification, we refer the generalized operator as Gaussian function with form as Eq. (13), 
gLoG as suggested in [15]. At best of our 
 ( )
 ( | ) ( ) 
 with a, b trigonometric functions to control the resulting from Eq. (13). The convolution products 
shape and the orientation with standard deviations of gLoG with the given image will be used to 
 determine the shape and the orientation of blobs. 
 and orientation θ. The gLoG 
 ( | ) is obtained by Eq. (14) 
 ( | ) ( | ) ( | ) ( ) 
 Discussion 
 Figure 7. Approximations of (a) with 표표 (b) with 표표 reformulations. 
 Dinh Cong Nguyen/ No.19_Dec 2020|p.47-56 
 For optimization, difference-of-offset-Gaussian between Gaussian functions with relatively small 
(DooG) operator is considered, which was first offset distances in Figure 7. The first derivative in x 
introduced by Young [17]. Basically, DooG dimension of the 2-D oriented Gaussian function 
function is designed by using Eq. (13) with offset Eq. (13) is given in Eq. (15), where a, b, c 
 parameters are defined in Eq. (13). The DooG 
values , as the distance between two 
Gaussian kernels [18]. It could be explained that the function Eq. (16) can approximate the Gaussian 
derivatives of a Gaussian function are derivative function Eq. (15). 
mathematically closely equal to discrete difference 
 Figure 8. (a) a character, responses in color map of (b) the LoG operator (c) the BSV 
 operator (d) the BSV after hysteresis thresholding. 
 ( | ) ( ) ( | ) ( ) 
 ( | ) ( | ) ( | ) 
 ( | ) ( ) 
 The DooG operator can be extended to the second derivative from the x or y dimensions Eq. (17). These 
operators approximate the second order derivatives of Gaussian . 
 ( | ) ( | ) ( | ) 
 ( | ) (17) 
 With ( | ) and ( | ) formulations, we can approximate the 
gLoG operator Eq. (14) as given in Eq. (18). 
 ( | ) ( | ) ( | ) ( ) 
 3.3 The BSV Operator location and a null response in the in-between edge 
 The BSV operator [4] is a LoG look-like area Figure 8(b), the BSV operator still guaranties a 
operator for stroke detection. It differs from the no null response Figure 8(c). Then, similar to edge 
blob-based strategy with LoG, that targets optimum detector the stroke elements can be obtained with 
 hysteresis thresholding Figure 8(d). 
response (10) with the scale parameter 
Eq. (12). The operator processes as an edge detector The BSV operator is close to Laplacian 
with a zero-crossing operation, where the optimum formulation Eq. (3). It results in the total 
 differential d of an image function f(x, y) convolved 
scale for edge detection ≪ . Whereas the 
 with a δ(x, y) operator Eq. (19). 
LoG operator produces a strong response at an edge 
 ( ) ( ( )) ( ) ( ) ( ) 
 Using the linearity property, the compound formulation of Biot-Savart law into an image 
operator BSV(x, y) = d(δ(x, y)) can be achieved in convolution operator as described from original 
Eq. (20) with ( ) ( ) as defined in paper [4] in detail. 
Eq. (21). This operator is expressed from the the 
 ( ) ( ( )) ( ) ( ) ( ) 
 ( ) ( ) ( ) 
 ( ) ( ) 
 Dinh Cong Nguyen/ No.19_Dec 2020|p.47-56 
 Discussion produce a LoG look-like function as Eq. (23) with 
 A convolution with the BSV operator is close to ( | ) ( | ) the Gaussian derivatives. 
a derivative product, but with specific steps and Compared to the LoG, the BSV operator enhances 
averaging. When a Gaussian averaging product is the central part of the kernel that maintains a 
embedded Eq. (22), the BSV operator tends to response in the in-between edge area
 ( ) ( ( | ) ( ) ) ( ) ( | ) ( ) ( ) 
 ( | ) ( | ) ( ) ( | ) ( ) ( ) 
 The compound operator BSV(x, y) of Eq. (20) is 
 such as shifting the 
not separable. The real-time property is coming complexity to O(Nω). 
from the operator size, as we have ≪ . If the DoG operator introduces a main 
However, optimization could be obtained with the optimization compared to the LoG operator, 
non-compound form of the operator (these aspects however the complexity O(Nω) is not parameter-
are not discussed in [4]). The Gaussian derivatives free. The recent trends with camera devices (e.g. 
 ( | ) ( | ) can be approximated smartphones, tablets) are to process up to 10-Mpx 
with DooG operators Eq. (16) then almost-Gaussian for image streaming at 30 to 60 frames per second 
 (FPS). However, as illustrated in Figure 9(a) the 
function (see section 4).The ( ) ( ) 
 DoG operator can guarantee the frame rate at a low 
are functions close to Haar-like features that could 
 resolution only (less then 2-Mpx). If a low 
be approximated with boxcar operators [13]. 
 resolution is sufficient for simple text scene image 
 4 Discussion on Real-time LoG Operators 
 Figure 9(a), it introduces character degradations 
 The baseline approach to process a LoG with complex scene images Figure 9(b). 
operator is the convolution product. The LoG 
 For optimization, the DoG operator can be 
function (3) is discretized to get a mask g of size ω 
 estimated with almost-Gaussian functions [13] [20]. 
× ω, applied in the product . The size This enters in an estimator cascade methodology 
of the mask is dependent on the σ parameter LoG ≈ DoG ≈ ̂ , where ̂ is the DoG 
(the typical size is for a full coverage of the estimator. Specifically, repeated filtering with the 
function [19]), requiring a complexity O(N ) averaging filters can be used to approximate a 
with N the image size (in pixels). Optimization is Gaussian filter, as given below Eq. (24) and shown 
obtained with the DoG function Eq. (5) that can be in Figure 10(a), with a desired standard deviation 
implemented with separable filters of size 1 × ω [19]. 
Figure 9. (a) image with text from with processing time /FPS of DoG/almost- Gaussian operators at different resolutions 
 with parameters 휎푠 (11) (b) degradations of text/characters at low resolutions with a complex scene image. 
 Dinh Cong Nguyen/ No.19_Dec 2020|p.47-56 
 ̂( | ) ∑ ( ) ( ) 
 I 
 n 
 Figure 10. Approximation process (a) approximation of Gaussian function after the successive 
 averaging (b) DoG can be obtained from approximation of Gaussian. 
 the Eq. (24) ( ) is a given box filter ( )
 ( ) 
function having a predefined size. The quality of 
approximation is based on the number of repeated From approximation of Gaussian in Eq. (24), it 
filtering n, certainly no more than 6. It can be becomes possible to approximate the DoG operator 
justified by Eq. (25) in order to obtain 
 by ̂ in (26) with two sets of box filter function. 
approximation of a Gaussian, as presented in [19], 
 Figure 10(b) gives a plot of Eq. (26). 
where ω is the width of the averaging filter. 
 ̂ ̂( | ) ( ) ̂( | ) ( )
 ∑ ( ) ( ) ∑ ( ) ( ) ( ) 
 operator is controlled through the stroke model 
 Obviously, the ( ) ( ) products 
from Eq. (26) is able to be obtained with integral paradigm for scale-invariance. The gLoG operator 
image at complexity O(N). As a result, approximation [15] guaranties the rotation and contrast-invariance. 
of DoG is possibly achieved with 2n accesses of All these operators are symmetric except the gLoG 
integral image, it therefore is parameter free. operator. The symmetric operators detect the 
 medical axes of characters that produces an 
 The DoG filter is then approximated as a linear 
 important number of keypoint candidates. These 
combination of several box filters . Then, box 
 keypoints must be post-processed for grouping. The 
coefficients must be found to minimize the 
 gLoG operator relaxes this constraint, it the 
approximation error. In [13], this is presented as an processes with a full primitive detection. Therefore, 
L1 regularized least-square problem that can be it is a time-consuming operator and is minimally 
solved with an optimization algorithm (e.g. LASSO compatible with a real-time strategy. However, it 
as detailed on the optimization aspects). The 
 could be approximated by the DooG operator, even 
experiments in [13] report that DoG estimator 
 with the ̂ operator. This point has been little 
achieves an acceleration at low scales 
 explored in the literature, it then could be a 
[1.5, 3.1], while maintaining a low average mean 
 promising solution. 
square error compared to the DoG. Figure 9(a) 
 5 Conclusions and Perspectives 
gives the processing time of the estimator over the 
 This paper has presented how the LoG operators 
different image resolutions and scales . 
 can be set and adapted for text detection problem 
 The BSV operator [4] is the edge-based 
 and made real-time with an estimator cascade 
operator while applying a hybrid strategy that 
 methodology. Some main perspectives and 
generates a blob detection from an edge detection 
 challenges remain. Firstly, the LoG operators for 
using a LoG look-like function. Although they get a 
 text detection have mainly been investigated with 
sake of time-efficiency, the edge-based operators 
 symmetric model. However, little work exists on 
perform a poor detection as an average. The LoG 
 the generalization case (i.e. gLoG operator). The 
 Dinh Cong Nguyen/ No.19_Dec 2020|p.47-56 
generalization can turn the operator into a stroke [11] J. Matas and L. Neumann, "Real-time lexicon-
detection for a better detection accuracy. Next, the free scene text localization and recognition," 
real-time methodology with estimator cascade PAMI, vol. 38.9, pp. 1872-1885, 2016. 
offers intermediate acceleration factors (≃ ×2 to 
 [12] D. Nguyen, M. Delalandre, D. Conte and T. 
×4). It processes as a Full-Search (FS) method in 
 Pham, "Perfor- mance evaluation of real-time 
the spatial domain with the fast estimation of the 
 and scale-invariant LoG operators for text 
operator product. Similar to template matching, 
 detection.," VISAPP, pp. 344-353, 2019. 
further acceleration could be obtained with FS-
 [13] V. Fragoso, G. Srivastava, A. Nagar, Z. Li, K. 
equivalent methods. 
 Park and M. Turk, "Cascade of Box (CABOX) 
 Bibliography 
 Filters for Optimal Scale Space 
[1] Q. Ye and D. Doermann, "A survey Text Approximation," CVPR, pp. 126-131. 
 detection and recognition in imagery," PAMI, 
 [14] D. Nguyen, M. Delalandre, D. Conte and T. 
 vol. 37.7, pp. 1480-1500, 2015. 
 Pham, "Fast RT‐LoG operator for scene text 
[2] R. Gomez and B. Shi, "ICDAR2017 robust detection," JRTIP, 2020. 
 reading challenge on COCO-Text," ICDAR, 
 [15] H. Kong, H. Akakin and S. Sarma, "A 
 pp. 1435-1443, 2017. 
 generalized Laplacian of Gaussian filter for 
[3] H. Yang and C. Wang, "An Improved System blob detection and its applications," Cyber, 
 For Real-Time Scene Text Recognition," Proc. vol. 43.6, pp. 1719-1733, 2013. 
 Mul., pp. 657-660, 2015. 
 [16] N. Makhfi and O. Bannay, "Scale-space 
[4] X. Girones and C. Julia, "Real-Time Text approach for character segmentation in 
 Localization in Natural Scene Images Using a scanned images of arabic document. J. . : 444 
 Linear Spatial Filter," ICDAR, pp. 1261-1268, (2016)," Theo. App. Infor. Tech, vol. 94.2, 
 2017. 2016. 
[5] S. Deshpande and R. Shriram, "Real time text [17] R. Young, "Gaussian derivative theory of 
 detection and recognition on hand held objects spatial vision: analysis of cortical cell 
 to assist blind people," Proc. Dyn. Opt. Tech, receptive field line-weighting profiles," 
 pp. 1020-1024, 2016. Motors Research Laboratories, 1985. 
[6] B. Epshtein, E. Ofek and Y. Wexler, [18] W. Ma and M. B.S., "EdgeFlow: a technique 
 "Detecting text in natural scenes with stroke for boundary detection and image 
 width transform," CVPR, pp. 2963-2970, 2010. segmentation," TIP, vol. 9.8, pp. 1375-1388, 
[7] L. Neumann and J. Matas, "Real-time scene 2000. 
 text localization and regconition," CVPR, pp. 
 [19] P. Kovesi, "Fast almost-gaussian filtering," 
 3538-3545, 2012. 
 Dig. Ima. Comp. Tech, pp. 21-125, 2010. 
[8] L. Neumann and J. Matas, "Scene text 
 [20] M. Grabner, H. Grabner and H. Bischof, "Fast 
 localization and regconition with oriented 
 approximated SIFT," ACCV, pp. 918-927, 
 stroke detection," ICCV, pp. 97-104, 2013. 
 2006. 
[9] L. Gomez and D. Karatzas, "MSER-based 
 [21] D. Sen and S. Pal, "Gradient histogram: 
 real-time text detection and tracking," in ICPR, 
 Thresholding in a region of interest for edge 
 2014. 
 detection," IVC, vol. 28.4, pp. 677-695, 2010. 
[10] Y. Liu, D. Zhang, Y. Zhang and S. Lin, "Real-
 time scene text detection based on stroke 
 model," ICPR, pp. 3116-3120, 2014. 
 Dinh Cong Nguyen/ No.19_Dec 2020|p.47-56 
 THẢO LUẬN VỀ CÁC TOÁN TỬ DỰA TRÊN LoG 
 ĐỂ PHÁT HIỆN VĂN BẢN THEO THỜI GIAN THỰC 
Dinh Cong Nguyen PhD 
Thông tin bài viết Tóm tắt 
 Trong bài báo này trình bày các phương pháp phát hiện văn bản thời gian thực 
Ngày nhận bài: trong hình ảnh dựa trên máy ảnh, tập trung đặc biệt vào toán tử Laplacian of 
20/9/2020 Gaussian (LoG). Các phương pháp này được thảo luận với sự tập trung cụ thể 
Ngày duyệt đăng: 
 vào các khía cạnh của tính phức tạp và tính mạnh mẽ. Một số kết quả minh họa 
10/12/2020 
 và các thí nghiệm cơ bản được đưa ra để mô tả đặc điểm của các phương pháp. 
 Hơn nữa, bài báo cũng cung cấp nhận xét về những cải tiến của các phương 
Từ khóa: pháp đối với vấn đề phát hiện văn bản. 
Phát hiện văn bản, toán tử 
LoG, mô hình đột quỵ, 
almost-Gaussian.