Determination of in situ detection efficiency for IM-NAA of non-standard geometrical samples

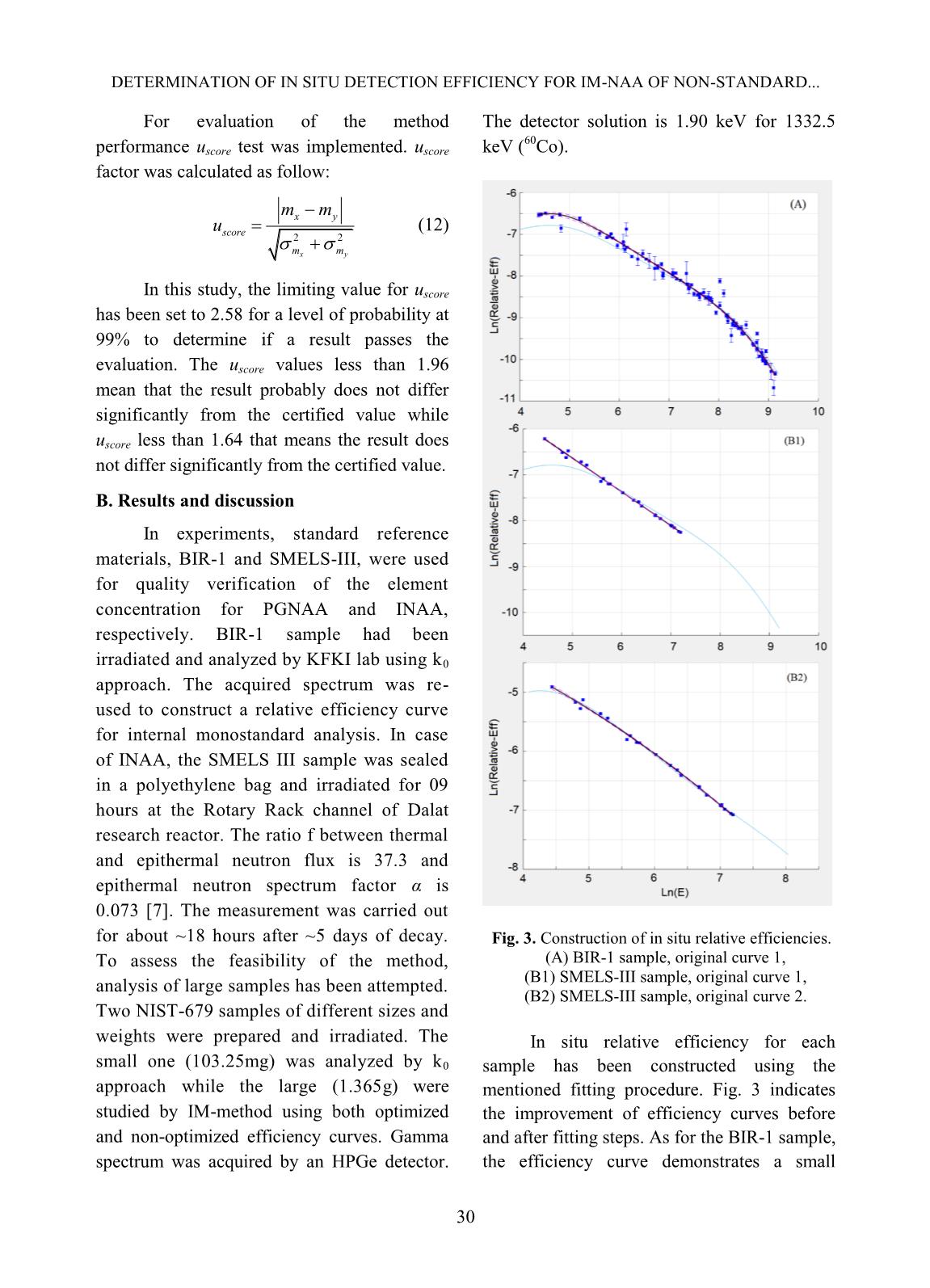
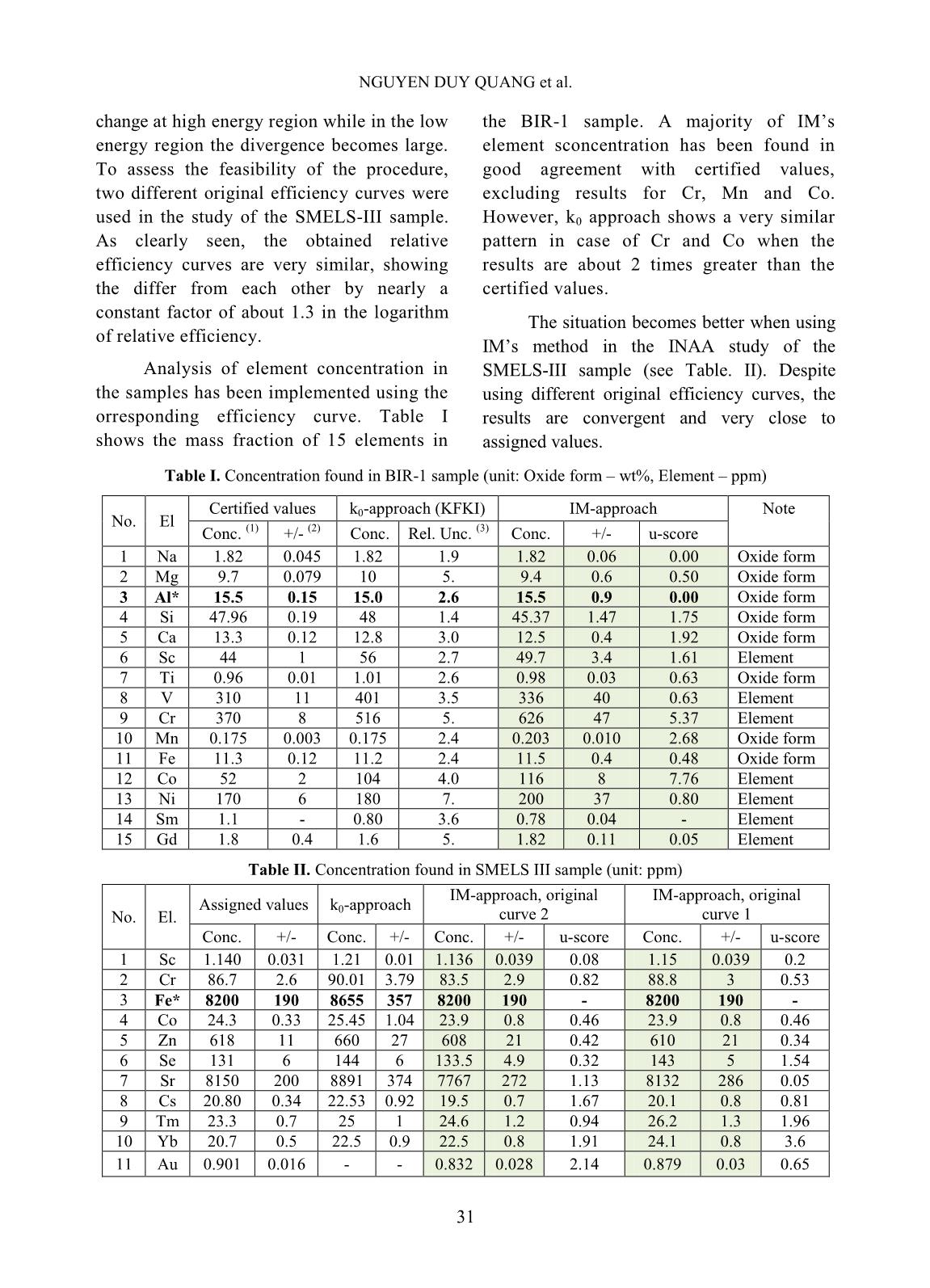
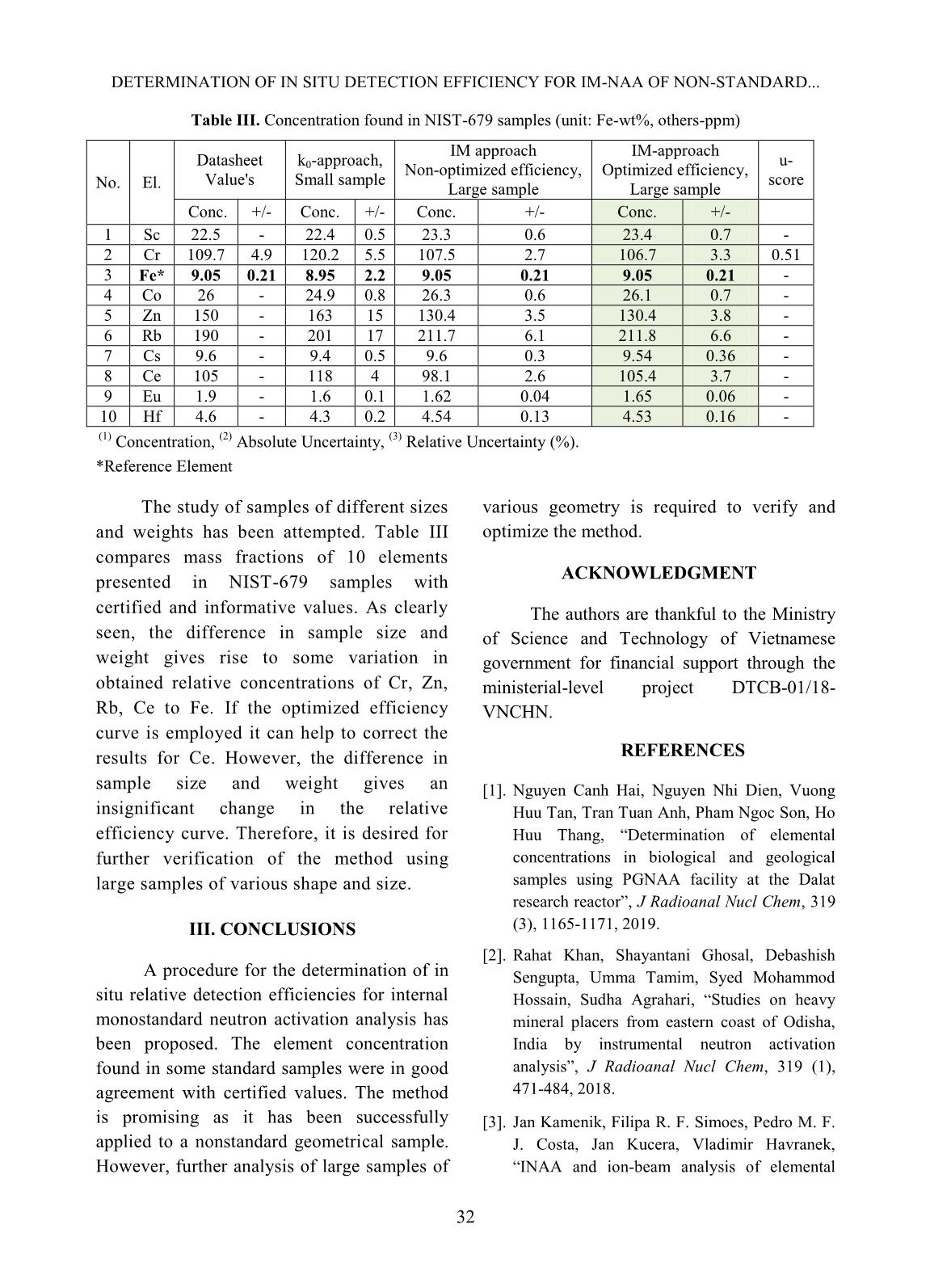
ncy plays a key role in the analysis as it 
is valuable to the correction of sample 
geometry effects [6]. In this study, a computer 
code for the determination of the in situ 
relative efficiency has been developed. Using 
Prompt Gamma NAA (PGNAA) and 
Instrumental NAA (INAA) nuclear data, the 
software requires only a peak area report file 
for calculation of relative efficiency and 
perform further analysis. Results from 
measurements of standard reference materials 
have been found to be in good agreement with 
certified values. 
II. CONTENT 
A. Subjects and methods 
In INAA using k0 approach, consider 
two arbitrary elements x and y presented in an 
activated sample which emits two series of 
DETERMINATION OF IN SITU DETECTION EFFICIENCY FOR IM-NAA OF NON-STANDARD... 
28 
characteristic gamma rays Ex,i and Ey,j (i, j = 1, 
2,...), respectively. The mass ratio of element x 
to y can be expressed as follow [5]: 
, , ,
, , ,
0,0
0 0,
( ( ( )))
( ( ( )))
x i y j y j
y j x i x i
E E Eyx
y x E E E
P kSDC f Qm
m SDC f Q P k
 
 
 (1) 
Where S is the saturation factor, D is 
the decay factor, C is the measurement 
factor, f is the ratio of the thermal to 
epithermal neutron fluxes, Q0( ) is the ratio 
of the resonance integral-to-thermal neutron 
cross-section corrected for the non-ideal 
epithermal neutron flux distribution (α), P is 
the peak area and ε is the full energy peak 
detection efficiency. In case of high f, the 
value of 
0 0( ( ))) / ( ( )))y xf Q f Q in eq. 
(1) tends to unity and therefore, eq. (1) can 
be simplified as: 
, , ,
, , ,
0,
0,
( )
( )
x i y j y j
y j x i x i
E E Eyx
y x E E E
P kSDCm
m SDC P k


 (2) 
The situation is very simple in case of 
PGNAA where the correction factors S, D and 
C can be eliminated. Though, it should be 
noted that the k0 databases for two different 
techniques are different. Having it in mind, the 
mass ratio in both INAA and PGNAA can be 
rewritten as: 
,,
, ,
y jx i
y j x i
EEx
y E E
cm
m c


 (3) 
Where c is the coefficient calculated 
using k0 database and experimental data 
,
,
,0 0,
( ) ( ( )))
x i
x i
x i
E
E
x x E
P
c
SDC f Q k 
 (4) 
and in some cases can be simplified as 
,
,
,0,
( )
x i
x i
x i
E
E
x E
P
c
SDC k
 (5) 
As clearly seen in eq. (3), the relative 
concentration of element x to y can be 
determined by the ratio of full peak detection 
efficiencies. This leads to the need for using 
relative detection efficiency which can be 
determined straightforwardly from eq. 3 using 
a fitting procedure. The relation of detection 
efficiencies is as follow: 
 ,
, ,
,
x i
y j x i
y j
E x
E E
E y
c m
c m
  (6) 
Hence, 
,
, ,
,
ln( ) ln ln ln( )
x i
y j x i
y j
Ex
E E
y E
cm
m c
 
 (7) 
The efficiencies at different gamma 
energies of each element are derived from 
eq. (6) 
,1
, ,1
,
ln( ) ln ln( ), 2,3,...
x
x i x
x i
E
E E
E
c
i
c
 
 (8) 
,1
, ,1
,
ln( ) ln ln( ), 2,3,...
y
y j y
y j
E
E E
E
c
j
c
 
 (9) 
Thus, relative efficiency curves in 
logarithmic scale constructed individually 
from each element are expected to be differed 
by constant factors, say t. Because of using 
relative efficiency, an arbitrary positive value 
can be firstly assigned to one detection 
efficiency of each element, e.g. 
,1
Arb 10%
kE
 
for any k-th element where “Arb” indicates 
the first choice of detection efficiency. The 
relative detection efficiencies are then 
corrected by t-factors: 
, ,
ln(Rel ) ln(Arb )
k i k iE E k
t  (10) 
In general, the expression for the relative 
efficiency curve is 
0
ln(Rel ( )) (ln )
n
i
i
i
E a E
  (11) 
NGUYEN DUY QUANG et al. 
29 
Where ai is the coefficient and n is the 
order of the polynomial that can be chosen 
depending on the energy range of interest. 
After the relative efficiency calibration curve 
(11) is constructed, the relative concentrations 
can be calculated from eq. (3) and converted to 
absolute concentration using a well-know mass 
fraction of an element presented in the sample. 
If the concentration of m elements are required 
to be analysed there will be m+n+1 parameters 
needed to be optimized in fitting procedure, 
including ai, i=0,1,..n and tk, k=1,2,...m. The 
iteration loop for determination of all 
mentioned parameters is presented in Fig. 1. 
The loop starts with a reference efficiency 
curve which is then used for the correction 
of experimental relative detection efficiency at 
different energies of all elements, i.e. 
calculation of all characteristic factors t in eq. 
10 (see Fig. 2). In the next step, least-square 
fitting is performed to construct a new 
efficiency curve. The Goodness Of Fit (GOF) 
in the fitting step is used for stop condition. 
The loop is forced to stop whenever the GOF 
starts to increase. On the other hand, it will 
stop if the number of the loop is large enough 
and the GOF is almost saturated. A typical 
curve corresponding to the detector used for 
spectrum acquisition may be chosen as the 
original reference efficiency curve. It has been 
found that the employment of different original 
reference efficiency curves gives a very small 
divergence on final analysis results. 
Fig.1. Iteration for optimization of fitting parameters 
Fig. 2. Illustration of relative efficiency correction for iron by tFe-factor. 
(a) before correction, (b) after correction 
DETERMINATION OF IN SITU DETECTION EFFICIENCY FOR IM-NAA OF NON-STANDARD... 
30 
For evaluation of the method 
performance uscore test was implemented. uscore 
factor was calculated as follow: 
2 2
x y
x y
score
m m
m m
u
 
 (12) 
In this study, the limiting value for uscore 
has been set to 2.58 for a level of probability at 
99% to determine if a result passes the 
evaluation. The uscore values less than 1.96 
mean that the result probably does not differ 
significantly from the certified value while 
uscore less than 1.64 that means the result does 
not differ significantly from the certified value. 
B. Results and discussion 
In experiments, standard reference 
materials, BIR-1 and SMELS-III, were used 
for quality verification of the element 
concentration for PGNAA and INAA, 
respectively. BIR-1 sample had been 
irradiated and analyzed by KFKI lab using k0 
approach. The acquired spectrum was re-
used to construct a relative efficiency curve 
for internal monostandard analysis. In case 
of INAA, the SMELS III sample was sealed 
in a polyethylene bag and irradiated for 09 
hours at the Rotary Rack channel of Dalat 
research reactor. The ratio f between thermal 
and epithermal neutron flux is 37.3 and 
epithermal neutron spectrum factor α is 
0.073 [7]. The measurement was carried out 
for about ~18 hours after ~5 days of decay. 
To assess the feasibility of the method, 
analysis of large samples has been attempted. 
Two NIST-679 samples of different sizes and 
weights were prepared and irradiated. The 
small one (103.25mg) was analyzed by k0 
approach while the large (1.365g) were 
studied by IM-method using both optimized 
and non-optimized efficiency curves. Gamma 
spectrum was acquired by an HPGe detector. 
The detector solution is 1.90 keV for 1332.5 
keV (
60
Co). 
Fig. 3. Construction of in situ relative efficiencies. 
(A) BIR-1 sample, original curve 1, 
(B1) SMELS-III sample, original curve 1, 
(B2) SMELS-III sample, original curve 2. 
In situ relative efficiency for each 
sample has been constructed using the 
mentioned fitting procedure. Fig. 3 indicates 
the improvement of efficiency curves before 
and after fitting steps. As for the BIR-1 sample, 
the efficiency curve demonstrates a small 
NGUYEN DUY QUANG et al. 
31 
change at high energy region while in the low 
energy region the divergence becomes large. 
To assess the feasibility of the procedure, 
two different original efficiency curves were 
used in the study of the SMELS-III sample. 
As clearly seen, the obtained relative 
efficiency curves are very similar, showing 
the differ from each other by nearly a 
constant factor of about 1.3 in the logarithm 
of relative efficiency. 
Analysis of element concentration in 
the samples has been implemented using the 
orresponding efficiency curve. Table I 
shows the mass fraction of 15 elements in 
the BIR-1 sample. A majority of IM’s 
element sconcentration has been found in 
good agreement with certified values, 
excluding results for Cr, Mn and Co. 
However, k0 approach shows a very similar 
pattern in case of Cr and Co when the 
results are about 2 times greater than the 
certified values. 
The situation becomes better when using 
IM’s method in the INAA study of the 
SMELS-III sample (see Table. II). Despite 
using different original efficiency curves, the 
results are convergent and very close to 
assigned values. 
Table I. Concentration found in BIR-1 sample (unit: Oxide form – wt%, Element – ppm) 
No. El 
Certified values k0-approach (KFKI) IM-approach Note 
 Conc. 
(1)
 +/- 
(2)
 Conc. Rel. Unc. 
(3)
 Conc. +/- u-score 
1 Na 1.82 0.045 1.82 1.9 1.82 0.06 0.00 Oxide form 
2 Mg 9.7 0.079 10 5. 9.4 0.6 0.50 Oxide form 
3 Al* 15.5 0.15 15.0 2.6 15.5 0.9 0.00 Oxide form 
4 Si 47.96 0.19 48 1.4 45.37 1.47 1.75 Oxide form 
5 Ca 13.3 0.12 12.8 3.0 12.5 0.4 1.92 Oxide form 
6 Sc 44 1 56 2.7 49.7 3.4 1.61 Element 
7 Ti 0.96 0.01 1.01 2.6 0.98 0.03 0.63 Oxide form 
8 V 310 11 401 3.5 336 40 0.63 Element 
9 Cr 370 8 516 5. 626 47 5.37 Element 
10 Mn 0.175 0.003 0.175 2.4 0.203 0.010 2.68 Oxide form 
11 Fe 11.3 0.12 11.2 2.4 11.5 0.4 0.48 Oxide form 
12 Co 52 2 104 4.0 116 8 7.76 Element 
13 Ni 170 6 180 7. 200 37 0.80 Element 
14 Sm 1.1 - 0.80 3.6 0.78 0.04 - Element 
15 Gd 1.8 0.4 1.6 5. 1.82 0.11 0.05 Element 
Table II. Concentration found in SMELS III sample (unit: ppm) 
No. El. 
Assigned values k0-approach 
IM-approach, original 
curve 2 
IM-approach, original 
curve 1 
Conc. +/- Conc. +/- Conc. +/- u-score Conc. +/- u-score 
1 Sc 1.140 0.031 1.21 0.01 1.136 0.039 0.08 1.15 0.039 0.2 
2 Cr 86.7 2.6 90.01 3.79 83.5 2.9 0.82 88.8 3 0.53 
3 Fe* 8200 190 8655 357 8200 190 - 8200 190 - 
4 Co 24.3 0.33 25.45 1.04 23.9 0.8 0.46 23.9 0.8 0.46 
5 Zn 618 11 660 27 608 21 0.42 610 21 0.34 
6 Se 131 6 144 6 133.5 4.9 0.32 143 5 1.54 
7 Sr 8150 200 8891 374 7767 272 1.13 8132 286 0.05 
8 Cs 20.80 0.34 22.53 0.92 19.5 0.7 1.67 20.1 0.8 0.81 
9 Tm 23.3 0.7 25 1 24.6 1.2 0.94 26.2 1.3 1.96 
10 Yb 20.7 0.5 22.5 0.9 22.5 0.8 1.91 24.1 0.8 3.6 
11 Au 0.901 0.016 - - 0.832 0.028 2.14 0.879 0.03 0.65 
DETERMINATION OF IN SITU DETECTION EFFICIENCY FOR IM-NAA OF NON-STANDARD... 
32 
Table III. Concentration found in NIST-679 samples (unit: Fe-wt%, others-ppm) 
No. El. 
Datasheet 
Value's 
k0-approach, 
Small sample 
IM approach 
Non-optimized efficiency, 
Large sample 
IM-approach 
Optimized efficiency, 
Large sample 
u-
score 
 Conc. +/- Conc. +/- Conc. +/- Conc. +/- 
1 Sc 22.5 - 22.4 0.5 23.3 0.6 23.4 0.7 - 
2 Cr 109.7 4.9 120.2 5.5 107.5 2.7 106.7 3.3 0.51 
3 Fe* 9.05 0.21 8.95 2.2 9.05 0.21 9.05 0.21 - 
4 Co 26 - 24.9 0.8 26.3 0.6 26.1 0.7 - 
5 Zn 150 - 163 15 130.4 3.5 130.4 3.8 - 
6 Rb 190 - 201 17 211.7 6.1 211.8 6.6 - 
7 Cs 9.6 - 9.4 0.5 9.6 0.3 9.54 0.36 - 
8 Ce 105 - 118 4 98.1 2.6 105.4 3.7 - 
9 Eu 1.9 - 1.6 0.1 1.62 0.04 1.65 0.06 - 
10 Hf 4.6 - 4.3 0.2 4.54 0.13 4.53 0.16 - 
 (1)
 Concentration, 
(2)
 Absolute Uncertainty, 
(3)
 Relative Uncertainty (%). 
*Reference Element 
The study of samples of different sizes 
and weights has been attempted. Table III 
compares mass fractions of 10 elements 
presented in NIST-679 samples with 
certified and informative values. As clearly 
seen, the difference in sample size and 
weight gives rise to some variation in 
obtained relative concentrations of Cr, Zn, 
Rb, Ce to Fe. If the optimized efficiency 
curve is employed it can help to correct the 
results for Ce. However, the difference in 
sample size and weight gives an 
insignificant change in the relative 
efficiency curve. Therefore, it is desired for 
further verification of the method using 
large samples of various shape and size. 
III. CONCLUSIONS 
A procedure for the determination of in 
situ relative detection efficiencies for internal 
monostandard neutron activation analysis has 
been proposed. The element concentration 
found in some standard samples were in good 
agreement with certified values. The method 
is promising as it has been successfully 
applied to a nonstandard geometrical sample. 
However, further analysis of large samples of 
various geometry is required to verify and 
optimize the method. 
ACKNOWLEDGMENT 
The authors are thankful to the Ministry 
of Science and Technology of Vietnamese 
government for financial support through the 
ministerial-level project DTCB-01/18-
VNCHN. 
REFERENCES 
[1]. Nguyen Canh Hai, Nguyen Nhi Dien, Vuong 
Huu Tan, Tran Tuan Anh, Pham Ngoc Son, Ho 
Huu Thang, “Determination of elemental 
concentrations in biological and geological 
samples using PGNAA facility at the Dalat 
research reactor”, J Radioanal Nucl Chem, 319 
(3), 1165-1171, 2019. 
[2]. Rahat Khan, Shayantani Ghosal, Debashish 
Sengupta, Umma Tamim, Syed Mohammod 
Hossain, Sudha Agrahari, “Studies on heavy 
mineral placers from eastern coast of Odisha, 
India by instrumental neutron activation 
analysis”, J Radioanal Nucl Chem, 319 (1), 
471-484, 2018. 
[3]. Jan Kamenik, Filipa R. F. Simoes, Pedro M. F. 
J. Costa, Jan Kucera, Vladimir Havranek, 
“INAA and ion-beam analysis of elemental 
NGUYEN DUY QUANG et al. 
33 
admixtures in carbon-based nanomaterials for 
battery electrodes”, J Radioanal Nucl Chem, 
318 (3), 2463-2472, 2018. 
[4]. Pasquale Avino, Geraldo Capannesi, Luigina 
Renzi, Alberto Rosada, “Physiological 
parameters affecting the hair element content of 
young Italian population”, J Radioanal Nucl 
Chem, 306 (3), 737-743, 2015. 
[5]. Sudarshan, K.; Nair, A. G. C.; Goswami, A. J. 
Radioanal. “A proposed k0 based methodology 
for neutron activation analysis of samples of 
non-standard geometry”, J Radioanal Nucl 
Chem, 256 (1), 93-98, 2003. 
[6]. A. G. C. Nair, R. Acharya, K. Sudarshan, S. 
Gangotra, A. V. R. Reddy, S. B. Manohar and 
A. Goswami. “Development of an internal 
monostandard instrumental neutron activation 
analysis method based on in situ detection 
efficiency for analysis of large and nonstandard 
geometry samples”, Anal. Chem. 75, 4868-
4874, 2003. 
[7]. Manh-Dung Ho, Quang-Thien Tran, Van-
Doanh Ho, Dong-Vu Cao, Thi-Sy Nguyen, 
“Quality evaluation of the k0-standardized 
neutron activation analysis at the Dalat research 
reactor”, J Radioanal Nucl Chem, 309 (1), 135-
143, 2016.