Design of a FPGA-based controller for power and period measurement in the start range of Dalat Nuclear Research Reactor

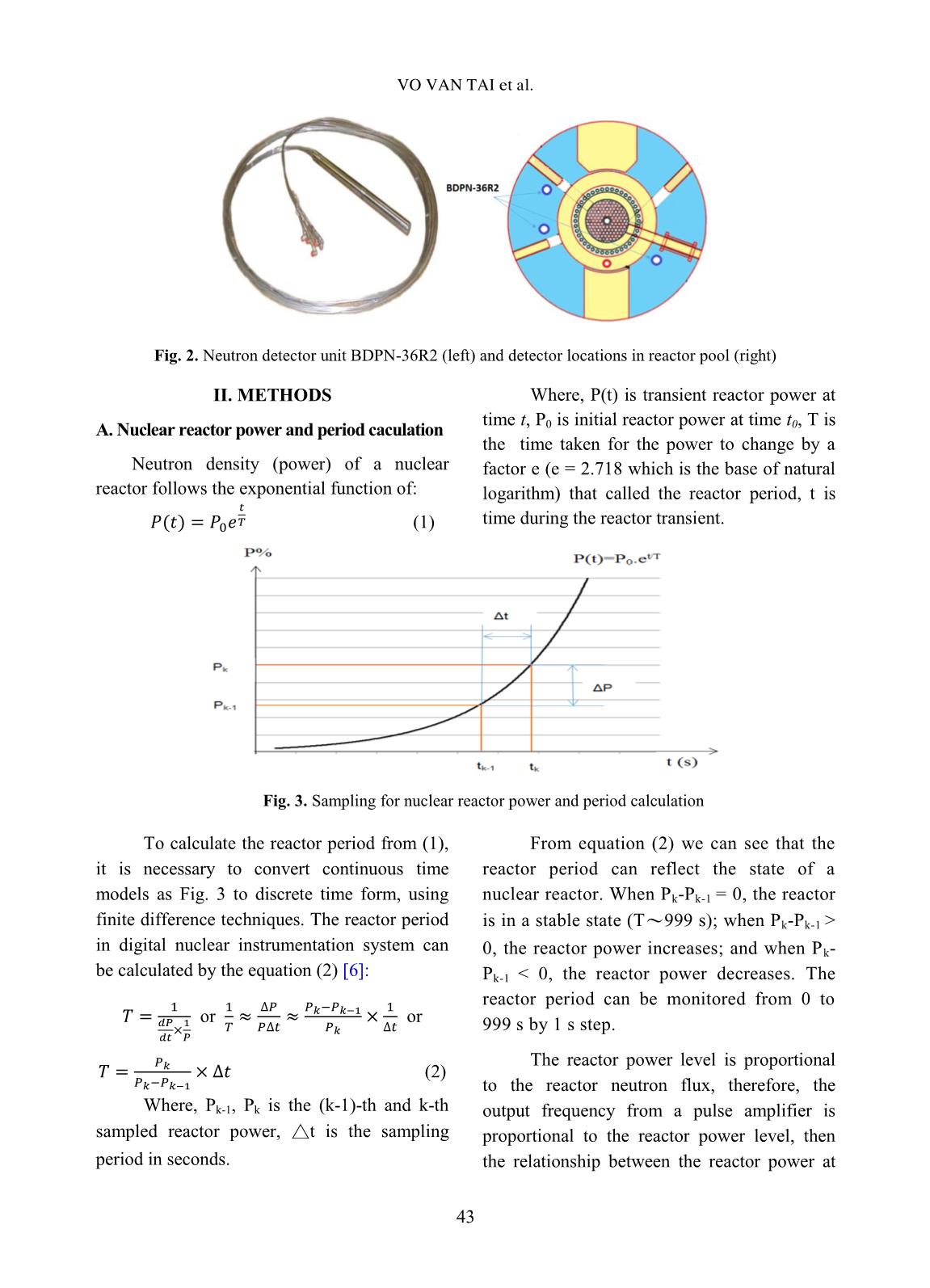
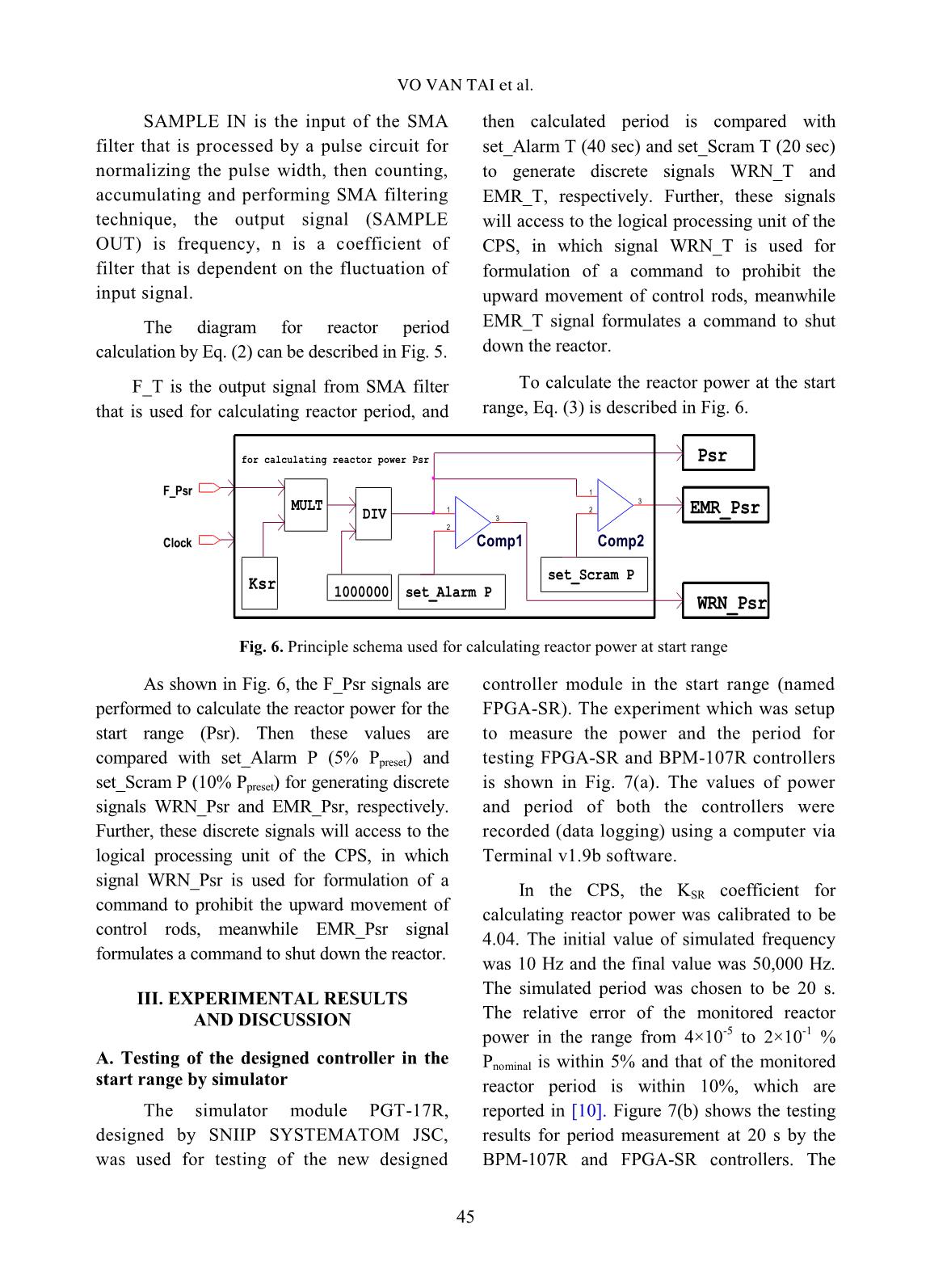
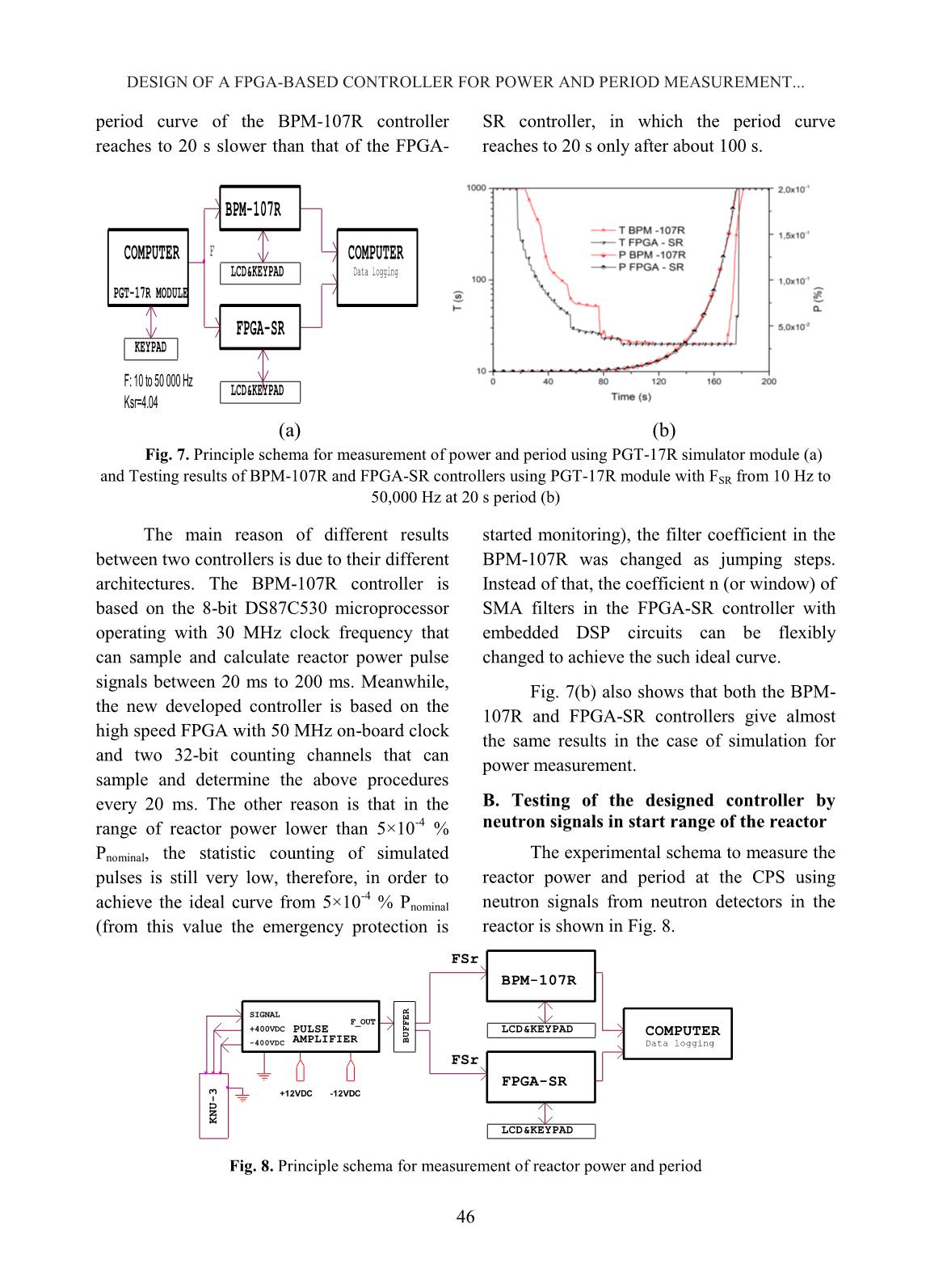
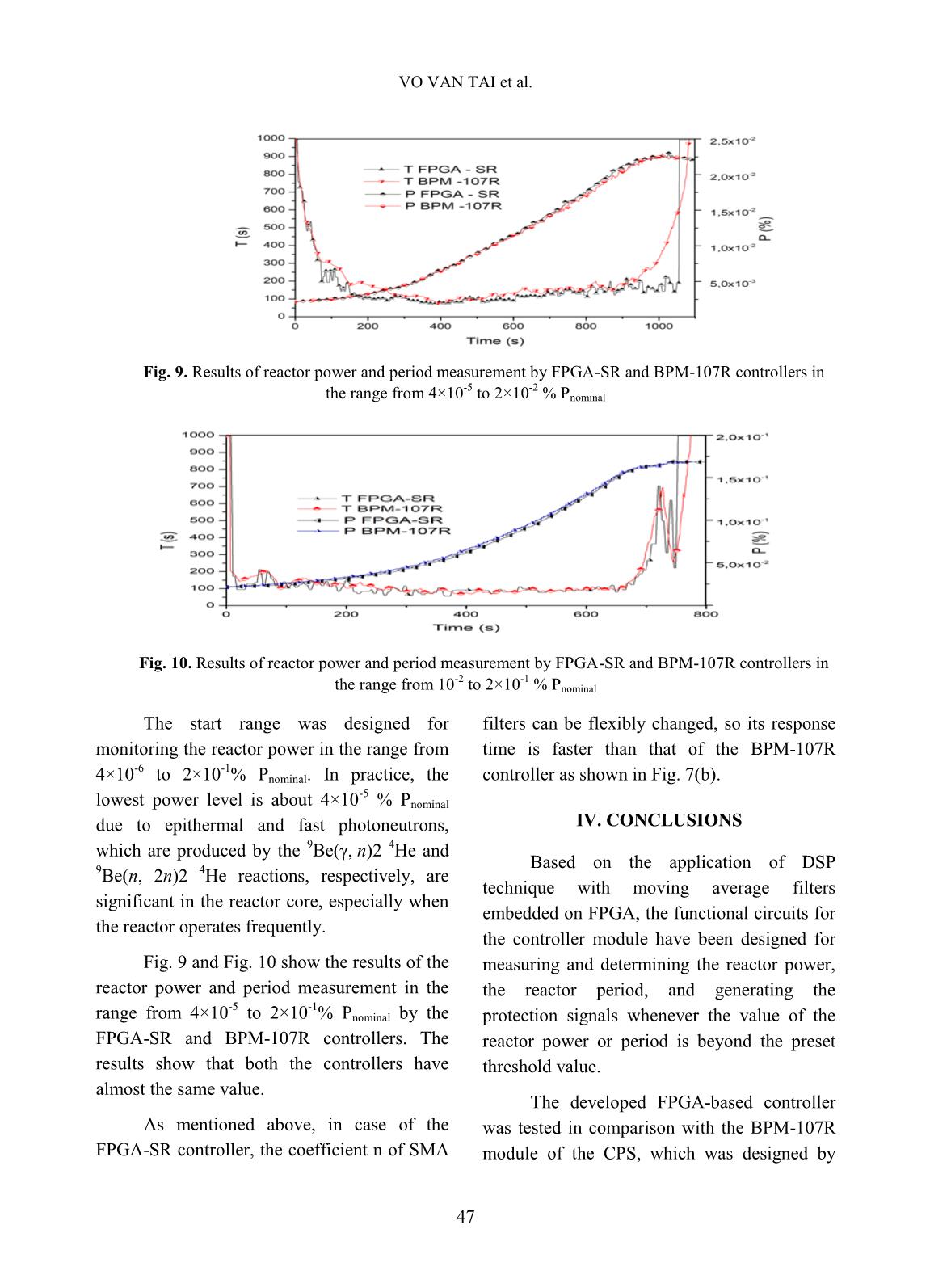
sing FPGA technology [4], and for 
nuclear data measurement by (n, γ) and (n, 2γ) 
reactions at horizontal experimental neutron 
beam ports of nuclear research reactor with high 
performance gamma spectrometers [5]. 
Considering the above-mentioned reasons and 
propensity, the main purpose of this work is to 
develop the new FPGA-based controller module 
which can be a spare-part or replacement for the 
BPM-107R controller when necessary. The 
developed controller applies DSP principle with 
moving average filtering technique using a Xilinx 
FPGA Artix-7 with on-board clock of 50 MHz 
and two 32-bit counting channels that can sample 
and calculate reactor power pulse signals every 
20 ms. Some comparisons with the current BPM-
107R controller module were performed by 
simulated signals as well as by real signals from 
neutron detectors of the start range. 
Fig. 1. The "2 out-of 3" data processing and architecture of the DNRR’ CPS 
(S – sensor/detector, C – Controller, L – Logic processing, R – Relay block, A – Actuator, 
D – Display panel) 
The CPS of DNRR is operating based on 
“2 out-of 3” principle as shown in Fig. 1. Three 
neutron detectors are installed in dry channels 
outside the reactor core, as shown in Fig. 2. 
S S
C
1 
D 
S
L1 L2 L3 
C2 C3 
R1 R2 R3 
A A 
 S2 
C1 
D 
 S1 S3 
VO VAN TAI et al. 
43 
Fig. 2. Neutron detector unit BDPN-36R2 (left) and detector locations in reactor pool (right) 
II. METHODS 
A. Nuclear reactor power and period caculation 
Neutron density (power) of a nuclear 
reactor follows the exponential function of: 
 (1) 
Where, P(t) is transient reactor power at 
time t, P0 is initial reactor power at time t0, T is 
the time taken for the power to change by a 
factor e (e = 2.718 which is the base of natural 
logarithm) that called the reactor period, t is 
time during the reactor transient. 
Fig. 3. Sampling for nuclear reactor power and period calculation 
To calculate the reactor period from (1), 
it is necessary to convert continuous time 
models as Fig. 3 to discrete time form, using 
finite difference techniques. The reactor period 
in digital nuclear instrumentation system can 
be calculated by the equation (2) [6]: 
 or 
 or 
 (2) 
Where, Pk-1, Pk is the (k-1)-th and k-th 
sampled reactor power, △t is the sampling 
period in seconds. 
From equation (2) we can see that the 
reactor period can reflect the state of a 
nuclear reactor. When Pk-Pk-1 = 0, the reactor 
is in a stable state (T〜999 s); when Pk-Pk-1 > 
0, the reactor power increases; and when Pk-
Pk-1 < 0, the reactor power decreases. The 
reactor period can be monitored from 0 to 
999 s by 1 s step. 
The reactor power level is proportional 
to the reactor neutron flux, therefore, the 
output frequency from a pulse amplifier is 
proportional to the reactor power level, then 
the relationship between the reactor power at 
DESIGN OF A FPGA-BASED CONTROLLER FOR POWER AND PERIOD MEASUREMENT... 
44 
the start range (PSR) and the output frequency 
of the pulse amplifier can be calculated as: 
PSR = KSR×FSR×10
-6
 (3) 
Where, PSR is the reactor power at the 
start range, KSR is a coefficient, FSR is the 
output frequency from the pulse amplifier 
which is connected to the fission chamber for 
monitoring in the range from 10
-6
 to 10
-1
 % 
Pnominal (Pnominal = 500 kWt). 
B. Design of moving average filters using 
FPGA and DSP 
A moving average (MA) filter is a 
type of finite impulse response filter (FIR) 
[7]. It is used widely in many applications 
in digital signal processing, 
communications, control, electrical and 
biomedical systems. The main purpose of 
MA filter is to increase the signal to noise 
ratio and to reduce random noise. 
A simple moving average (SMA) filter 
is a filter that averages N points of previous 
inputs and makes an output with them, the 
formula is expressed as follows: [8, 9] 
1
1 ( 1)
0
..... 1 nM M M n
SM M i
i
P P P
P P
n n
 
(4)
When calculating sequential values, a 
new value comes into the sum, and the oldest 
value moves out, n is coefficient or window of 
filter. Equation (4) can be rewritten as: 
, r
1
( )SM SM p e M M nP P P P
n
 (5) 
Where, SMP is the average value, , rSM p eP
is the previous average, MP is the new sample, 
M nP is the n-th old sample, n is the window 
of SMA filter. 
Equation (5) can be described in Fig. 4, 
in which the reactor power and the reactor 
period are calculated by DSP technique 
embedded on FPGA. 
Fig. 4. Principle schema used for moving average filter 
Fig. 5. Principle schema used for calculating reactor period
SAMPLE IN
Pulse
circuit SAMPLE OUT
Clock
Xi
Z(-n)
Yi
n
DIVSUB
Z(-1)
ADD
SMA Filter
INVERSE
WRM_T
EMR_T
set_Scram T=20s
F_T
set_Alarm T=40 s
T
Comp5
1
3
2
Clock
Comp6
1
3
2
Dt
Z(-1)
MULT
MULT
for calculating reactor period
SUB
VO VAN TAI et al. 
45 
SAMPLE IN is the input of the SMA 
filter that is processed by a pulse circuit for 
normalizing the pulse width, then counting, 
accumulating and performing SMA filtering 
technique, the output signal (SAMPLE 
OUT) is frequency, n is a coefficient of 
filter that is dependent on the fluctuation of 
input signal. 
The diagram for reactor period 
calculation by Eq. (2) can be described in Fig. 5. 
F_T is the output signal from SMA filter 
that is used for calculating reactor period, and 
then calculated period is compared with 
set_Alarm T (40 sec) and set_Scram T (20 sec) 
to generate discrete signals WRN_T and 
EMR_T, respectively. Further, these signals 
will access to the logical processing unit of the 
CPS, in which signal WRN_T is used for 
formulation of a command to prohibit the 
upward movement of control rods, meanwhile 
EMR_T signal formulates a command to shut 
down the reactor. 
To calculate the reactor power at the start 
range, Eq. (3) is described in Fig. 6. 
Fig. 6. Principle schema used for calculating reactor power at start range 
As shown in Fig. 6, the F_Psr signals are 
performed to calculate the reactor power for the 
start range (Psr). Then these values are 
compared with set_Alarm P (5% Ppreset) and 
set_Scram P (10% Ppreset) for generating discrete 
signals WRN_Psr and EMR_Psr, respectively. 
Further, these discrete signals will access to the 
logical processing unit of the CPS, in which 
signal WRN_Psr is used for formulation of a 
command to prohibit the upward movement of 
control rods, meanwhile EMR_Psr signal 
formulates a command to shut down the reactor. 
III. EXPERIMENTAL RESULTS 
AND DISCUSSION 
A. Testing of the designed controller in the 
start range by simulator 
The simulator module PGT-17R, 
designed by SNIIP SYSTEMATOM JSC, 
was used for testing of the new designed 
controller module in the start range (named 
FPGA-SR). The experiment which was setup 
to measure the power and the period for 
testing FPGA-SR and BPM-107R controllers 
is shown in Fig. 7(a). The values of power 
and period of both the controllers were 
recorded (data logging) using a computer via 
Terminal v1.9b software. 
In the CPS, the KSR coefficient for 
calculating reactor power was calibrated to be 
4.04. The initial value of simulated frequency 
was 10 Hz and the final value was 50,000 Hz. 
The simulated period was chosen to be 20 s. 
The relative error of the monitored reactor 
power in the range from 4×10
-5
 to 2×10
-1
 % 
Pnominal is within 5% and that of the monitored 
reactor period is within 10%, which are 
reported in [10]. Figure 7(b) shows the testing 
results for period measurement at 20 s by the 
BPM-107R and FPGA-SR controllers. The 
set_Scram P
Ksr
F_Psr
MULT EMR_Psr
for calculating reactor power Psr
Clock
WRN_Psr
Comp2
1
3
2
Psr
Comp1
1
3
2
1000000 set_Alarm P
DIV
DESIGN OF A FPGA-BASED CONTROLLER FOR POWER AND PERIOD MEASUREMENT... 
46 
period curve of the BPM-107R controller 
reaches to 20 s slower than that of the FPGA- 
SR controller, in which the period curve 
reaches to 20 s only after about 100 s. 
(a) (b) 
Fig. 7. Principle schema for measurement of power and period using PGT-17R simulator module (a) 
and Testing results of BPM-107R and FPGA-SR controllers using PGT-17R module with FSR from 10 Hz to 
50,000 Hz at 20 s period (b) 
The main reason of different results 
between two controllers is due to their different 
architectures. The BPM-107R controller is 
based on the 8-bit DS87C530 microprocessor 
operating with 30 MHz clock frequency that 
can sample and calculate reactor power pulse 
signals between 20 ms to 200 ms. Meanwhile, 
the new developed controller is based on the 
high speed FPGA with 50 MHz on-board clock 
and two 32-bit counting channels that can 
sample and determine the above procedures 
every 20 ms. The other reason is that in the 
range of reactor power lower than 5×10
-4
 % 
Pnominal, the statistic counting of simulated 
pulses is still very low, therefore, in order to 
achieve the ideal curve from 5×10
-4
 % Pnominal 
(from this value the emergency protection is 
started monitoring), the filter coefficient in the 
BPM-107R was changed as jumping steps. 
Instead of that, the coefficient n (or window) of 
SMA filters in the FPGA-SR controller with 
embedded DSP circuits can be flexibly 
changed to achieve the such ideal curve. 
Fig. 7(b) also shows that both the BPM-
107R and FPGA-SR controllers give almost 
the same results in the case of simulation for 
power measurement. 
B. Testing of the designed controller by 
neutron signals in start range of the reactor 
The experimental schema to measure the 
reactor power and period at the CPS using 
neutron signals from neutron detectors in the 
reactor is shown in Fig. 8. 
Fig. 8. Principle schema for measurement of reactor power and period 
F
F: 10 to 50 000 Hz
KEYPAD
Data logging
PGT-17R MODULE
Ksr=4.04
LCD&KEYPAD
COMPUTER
FPGA-SR
BPM-107R
COMPUTER
LCD&KEYPAD
FSr
-400VDC
+12VDC
B
U
F
F
E
R
COMPUTER
-12VDC
LCD&KEYPAD
SIGNAL
K
N
U
-
3
+400VDC
BPM-107R
F_OUT
PULSE
AMPLIFIER Data logging
FPGA-SR
LCD&KEYPAD
FSr
VO VAN TAI et al. 
47 
Fig. 9. Results of reactor power and period measurement by FPGA-SR and BPM-107R controllers in 
the range from 4×10
-5
 to 2×10
-2
 % Pnominal 
Fig. 10. Results of reactor power and period measurement by FPGA-SR and BPM-107R controllers in 
the range from 10
-2
 to 2×10
-1
 % Pnominal 
The start range was designed for 
monitoring the reactor power in the range from 
4×10
-6
 to 2×10
-1
% Pnominal. In practice, the 
lowest power level is about 4×10
-5
 % Pnominal 
due to epithermal and fast photoneutrons, 
which are produced by the 
9Be(γ, n)2 4He and 
9
Be(n, 2n)2 
4
He reactions, respectively, are 
significant in the reactor core, especially when 
the reactor operates frequently. 
Fig. 9 and Fig. 10 show the results of the 
reactor power and period measurement in the 
range from 4×10
-5
 to 2×10
-1
% Pnominal by the 
FPGA-SR and BPM-107R controllers. The 
results show that both the controllers have 
almost the same value. 
As mentioned above, in case of the 
FPGA-SR controller, the coefficient n of SMA 
filters can be flexibly changed, so its response 
time is faster than that of the BPM-107R 
controller as shown in Fig. 7(b). 
IV. CONCLUSIONS 
Based on the application of DSP 
technique with moving average filters 
embedded on FPGA, the functional circuits for 
the controller module have been designed for 
measuring and determining the reactor power, 
the reactor period, and generating the 
protection signals whenever the value of the 
reactor power or period is beyond the preset 
threshold value. 
The developed FPGA-based controller 
was tested in comparison with the BPM-107R 
module of the CPS, which was designed by 
DESIGN OF A FPGA-BASED CONTROLLER FOR POWER AND PERIOD MEASUREMENT... 
48 
SNIIP SYSTEMATON JSC of Russia. The 
testing was performed both by pulse-generated 
simulator PGT-17R and by real neutron signals 
from the reactor. The experimental results of 
measuring reactor power and period by the 
FPGA-SR and BPM-107R controllers indicate 
a good agreement of their functions and 
characteristics, including the reactor power 
measured in the range from 4×10
-5
 to 2×10
-1
 % 
Pnominal with the accuracy less than 5% and the 
reactor period is monitored in the range from 1 
to 999 s with the accuracy less than 10%. 
Additionally, the emergency protection signal 
EMR-P or EMR-T is generated, when the 
reactor power is greater than Ppreset by 10% or 
the period is less than 20 s. 
The obtained results also permit to 
conclude that the new developed FPGA-based 
controller meets the design purposes and can 
perform all functions of the existing BPM-
107R controller, therefore, it can replace the 
BPM-107R controller when needed. 
ACKNOWLEDGEMENTS 
The authors are thankful to Dalat 
Nuclear Research Institute and Vietnam 
Atomic Energy Institute for their 
administrative assistance. This research is 
supported by Ministry of Science and 
Technology of Vietnam under grant number 
ĐTCB. 08/19/VNCHN. 
REFERENCES 
[1]. Complex of Equipment for Control and 
Protection System ASUZ-14R, Operating 
Manual RUNK.506319.004 RE-E, JSC 
SNIIP SYSTEMATOM, Chief Designer А. 
А. Zaikin, 2006. 
[2]. Safety Analysis Report for the Dalat Nuclear 
Research Reactor, Dalat Nuclear Research 
Institute, Chief Editor Nguyen Nhi Dien, 2012. 
[3]. Buzzetti S., Capou M., Guazzoni C. et al., 
“High-speed FPGA based pulse-height 
analyzer for high resolution x-ray 
spectroscopy”, IEEE Trans. Nucl. Sci. 52, pp. 
854–860, 2005. 
[4]. V. H. Hai, N. Q. Dao and M. Nomachi, 
“Cosmic ray angular distribution employing 
plastic scintillation detectors and flash-
ADC/FPGA-based readout systems”, 
Kerntechnik, 77, pp. 462–464, 2012. 
[5]. Pham Dinh Khang, Nguyen Nhi Dien, Dang 
Lanh, Nguyen Xuan Hai, Pham Ngoc Tuan, 
Nguyen Duc Hoa, Nguyen An Son, “A design 
configuration of an FPGA-based coincident 
spectrometry system”, J. of Analytical 
Sciences, Methods and Instrumentation, 2164–
2745, Vol. 3, pp. 158–162, 2013. 
[6]. E. P. Gytfopoulos and P.M. Coble, A digital 
nuclear reactor control system, 1960. 
[7]. Huasheng Xiong, Duo Li, “Nuclear reactor 
doubling time calculation using FIR filter”, 
Energy Procedia, 39, pp. 3–11, 2013. 
[8]. “Moving average” 
https://en.wikipedia.org/wiki/Moving_average 
[9]. The Scientist and Engineer's Guide to Digital 
Signal Processing, by Steven W. Smith, 
Chapter 15 “Moving average filters” pp. 277–
284, https://dspguide.com. 
[10]. Complex of Equipment for Control and 
Protection System ASUZ-14R, Passport 
RUNK.506319.004 PS-E, JSC SNIIP 
SYSTEMATOM, Chief Designer А. А. 
Zaikin, 2006.