Đề cương ôn tập kiểm tra học kỳ II môn Toán Lớp 12 - Năm học 2020-2021 - Trường THPT Lương Ngọc Quyến
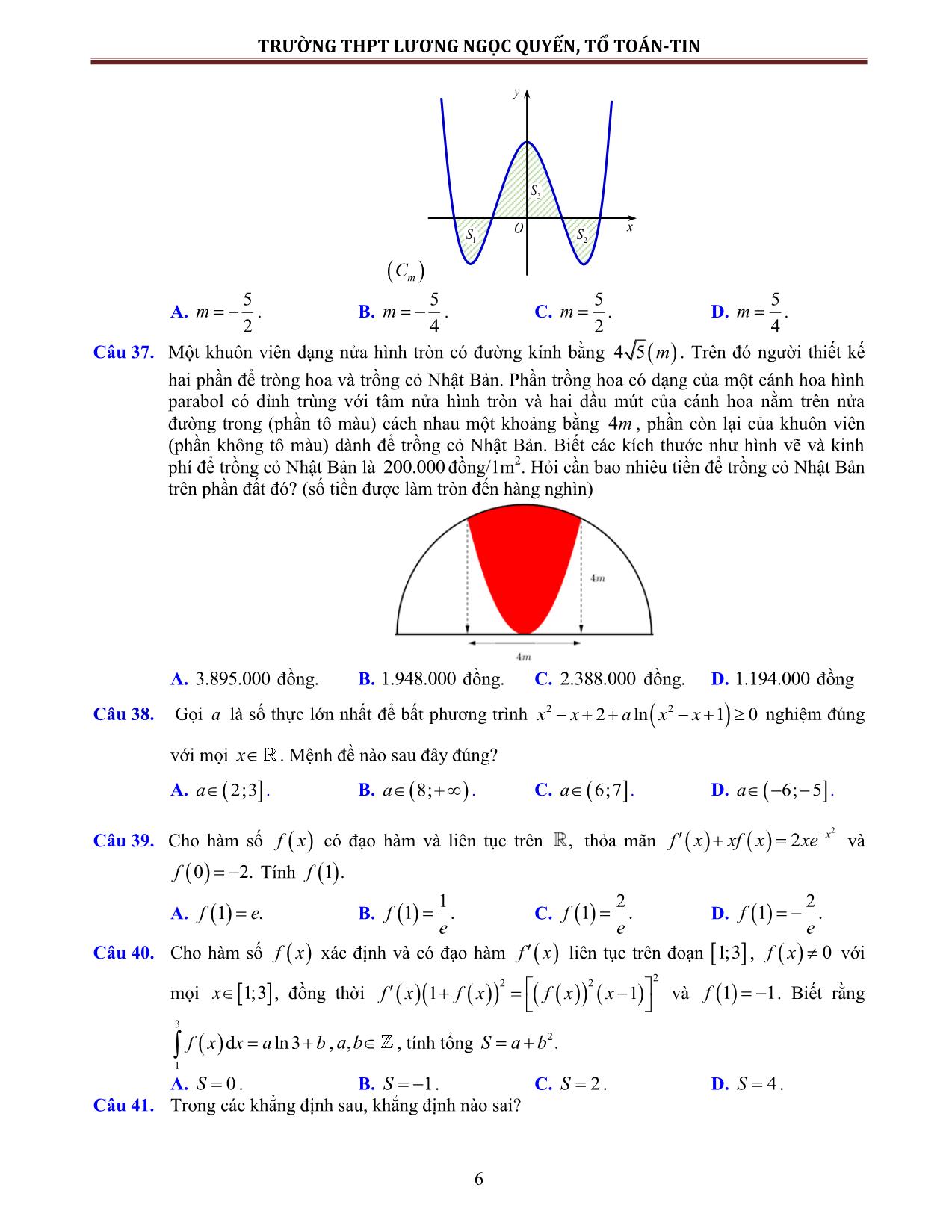
Câu 37. Một khuôn viên dạng nửa hình tròn có đường kính bằng 4 5m. Trên đó người thiết kế
hai phần để tròng hoa và trồng cỏ Nhật Bản. Phần trồng hoa có dạng của một cánh hoa hình
parabol có đỉnh trùng với tâm nửa hình tròn và hai đầu mút của cánh hoa nằm trên nửa
đường trong (phần tô màu) cách nhau một khoảng bằng 4m , phần còn lại của khuôn viên
(phần không tô màu) dành để trồng cỏ Nhật Bản. Biết các kích thước như hình vẽ và kinh
phí để trồng cỏ Nhật Bản là 200.000 đồng/1m2. Hỏi cần bao nhiêu tiền để trồng cỏ Nhật Bản
trên phần đất đó? (số tiền được làm tròn đến hàng nghìn)
A. 3.895.000 đồng. B. 1.948.000 đồng. C. 2.388.000 đồng. D. 1.194.000 đồng

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
Trang 6

Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Đề cương ôn tập kiểm tra học kỳ II môn Toán Lớp 12 - Năm học 2020-2021 - Trường THPT Lương Ngọc Quyến

y t z t . C. 11 5 : 23 32 5 x t y t z t . D. 13 5 : 17 104 5 x t y t z t . Câu 181 (TH). Trong không gian Oxyz, cho ba điểm 3;0;0A , 0;3;0B , 0;0;3C . Phương trình hình chiếu của đường thẳng OA trên mặt phẳng ABC là TRƯỜNG THPT LƯƠNG NGỌC QUYẾN, TỔ TOÁN-TIN 23 A. 3 2 x t y t z t . B. 3 4 x t y t z t . C. 3 0 0 x t y z . D. 1 2 1 1 x t y t z t . Câu 182 (TH). Trong không gian với hệ trục tọa độ Oxyz , viết phương trình đường thẳng đi qua điểm 2;4;3 A và vuông góc với mặt phẳng : 2 3 6 19 0 x y z . A. 2 4 3 2 3 6 x y z . B. 2 3 6 2 4 3 x y z . C. 2 4 3 2 3 6 x y z . D. 2 3 6 2 4 3 x y z . Câu 183 (TH). Trong không gian với hệ trục Oxyz , cho điểm 1;2; 1 A và mặt phẳng : 6 3 2 0 P x y z m ( m là tham số ). Tìm các giá trị thực của tham số m sao cho khoảng cách từ điểm A đến mặt phẳng P bằng 1. A. 1 m . B. 1 m . C. 3 m . D. 5 m . Câu 184 (TH). Trong không gian với hệ toạ độ Oxyz , viết phương trình mặt phẳng ( )P chứa điểm 1; 4;3 M và cắt các tia Ox , Oy , Oz lần lượt tại các điểm A , B , C sao cho 2 3 5 OA OB OC A. 15 10 6 7 0 x y z . B. 15 10 6 7 0 x y z . C. 15 10 6 7 0 x y z . D. 15 10 6 7 0 x y z . Câu 185 (TH). Mặt phẳng ( )P đi qua 3 điểm không thẳng hàng A(1;1;3); B( 1;2;3); ( 1;1;2) C có phương trình là: A. 2 2z 3 0 x y . B. 3z 3 0 x y . C. 2 2z+3 0 x y . D. z+3 0 x y . Câu 186 (TH). Tìm tọa độ điểm M trên trục Ox cách đều hai điểm 1 ; 2 ; 1 A và điểm 2 ; 1 ; 2B . A. 1 ; 0 ; 0 3 M . B. 1 ; 0 ; 0 2 M . C. 3 ; 0 ; 0 2 M . D. 2 ; 0 ; 0 3 M . Câu 187 (TH). Trong không gian với hệ tọa độ Oxyz , cho véc tơ 1;1; 2 , 1;0; u v m . Tìm tất cả giá trị của m để góc giữa u , v bằng 45 . A. 2 m . B. 2 6 m . C. 2 6 m . D. 2 6 m . Câu 188 (TH). Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC với 1;2; 3 A , 2;5;7B , 3;1;4 C . Điểm D để tứ giác ABCD là hình bình hành là A. 8 8 0; ; 3 3 D . B. 6;6;0D . C. 4; 2; 6 D . D. 0;8;8D . Câu 189 (TH). Cho hai điểm 1;0; 3 A và 3;2;1B . Phương trình mặt cầu đường kính AB là: A. 2 2 2 4 2 2 0. x y z x y z B. 2 2 2 4 2 2 0. x y z x y z TRƯỜNG THPT LƯƠNG NGỌC QUYẾN, TỔ TOÁN-TIN 24 C. 2 2 2 2 6 0. x y z x y z D. 2 2 2 4 2 2 6 0. x y z x y z Câu 190 (TH). Trong không gian với hệ tọa độ ,Oxyz 3 ; 4 ; 2 A , 5 ; 6 ; 2 B , 10 ; 17 ; 7 C . Viết phương trình mặt cầu tâm C bán kính AB . A. 2 2 2 10 17 7 8 x y z . B. 2 2 2 10 17 7 8 x y z . C. 2 2 2 10 17 7 8 x y z . D. 2 2 2 10 17 7 8 x y z . Câu 191 (VD). Trong không gian với hệ trục tọa độ Oxyz , cho điểm 1;5;2M và đường thẳng 1 5 3 : 2 1 1 x y z . Gọi là mặt phẳng đi qua M và cắt các tia , ,Ox Oy Oz lần lượt tại , ,A B C sao cho 2 2 2 1 1 1 OA OB OC đạt giá trị nhỏ nhất. Côsin góc giữa đường thẳng và đường thẳng BC bằng A. 147 58 . B. 174 85 . C. 417 58 . D. 174 58 . Câu 192 (VD). Trong không gian Oxyz , cho 1 : 1 4 x t d y t z t . Gọi A là điểm thuộc đường thẳng d ứng với giá trị 1 t . Phương trình mặt cầu tâm A tiếp xúc với : 2 2 9 0 P x y z là A. 2 2 2 2 3 1 2 x y z . B. 2 2 2 2 3 1 4 x y z . C. 2 2 2 2 3 1 4 x y z . D. 2 2 2 2 3 1 2 x y z . Câu 193 (VD). Trong không gian với hệ tọa độ Oxyz , cho hình hộp chữ nhật . ' ' ' 'ABCD A B C D có đỉnh A trùng với gốc tọa độ O , các đỉnh ( ;0;0)B m , (0; ;0)D m , '(0;0; )A n với , 0 m n và 5. m n Gọi M là trung điểm của cạnh 'CC . Tìm giá trị lớn nhất của thể tích khối tứ diện 'BDA M . A. 245 108 . B. 4 9 . C. 250 27 . D. 64 27 . Câu 194 (VD). Trong không gian Oxyz , cho ba điểm 1;2;2 A , 3; 1; 2 B , 4;0;3 C . Tìm tọa độ điểm I trên mặt phẳng Oxz sao cho biểu thức 2 5 IA IB IC đạt giá trị nhỏ nhất. A. 37 19 ;0; 4 4 I . B. 37 23 ;0 ; 4 4 I . C. 27 21 ;0 ; 4 4 I . D. 25 19 ;0 ; 4 4 I . Câu 195 (VD). Trong không gian Oxyz , cho hai điểm 1; 0; 0 , 2;1; 2 A B và mặt phẳng P có phương trình: 2 2 2019 0 x y z . Phương trình mặt phẳng Q đi qua hai điểm ,A B và tạo với mặt phẳng P một góc nhỏ nhất có phương trình là: A. 9 5 7 9 0 x y z . B. 5 2 1 0 x y z . C. 2 3 2 0 x y z . D. 2 2 2 2 0 x y z . TRƯỜNG THPT LƯƠNG NGỌC QUYẾN, TỔ TOÁN-TIN 25 Câu 196 (VD). Trong không gian Oxyz , cho điểm 1 ;2 ; 2 H . Mặt phẳng đi qua H và cắt các trục Ox , Oy , Oz tại A , B , C sao cho H là trực tâm tam giác ABC . Viết phương trình mặt cầu tâm O và tiếp xúc với mặt phẳng . A. 2 2 2 81 x y z . B. 2 2 2 1 x y z . C. 2 2 2 9 x y z . D. 2 2 2 25 x y z . Câu 197 (VD) . Cho đường thẳng d là giao tuyến của hai mặt phẳng ( ) : 2 2 1 0 P x y z và mặt phẳng ( ) : 2 2 4 0 Q x y z . Mặt cầu ( )S có phương trình 2 2 2 4 6 0 x y z x y m . Tìm m để đường thẳng ( )d cắt mặt cầu ( )S tại hai điểm phân biệt A , B sao cho 8 AB . A. 12 . B. 9 . C. 5 . D. 2 . Câu 198 (VDC). Cho điểm (2;5;1)A , mặt phẳng ( ) : 6 3 2 24 0 P x y z , H là hình chiếu vuông góc của A trên mặt phẳng ( )P . Phương trình mặt cầu ( )S có diện tích 784 và tiếp xúc với mặt phẳng ( )P tại H sao cho điểm A nằm trong mặt cầu là: A. 2 2 2 16 4 7 196 x y z . B. 2 2 2 16 4 7 196 x y z . C. 2 2 2 8 8 1 196 x y z . D. 2 2 2 8 8 1 196 x y z . Câu 199 (VDC). Trong không gian với hệ tọa độ Oxyz , cho điểm 1;2;3M . Gọi P là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng P cắt các trục tọa độ tại các điểm A , B , C . Tính thể tích khối chóp .O ABC . A. 1372 9 . B. 524 3 . C. 686 9 . D. 343 9 . Câu 200 (VDC). Trong không gian với hệ tọa độ Oxyz cho ba điểm A 1;1;1 ; B 1;2;0 ; C 3; 1;2 . Điểm M ; ;a b c thuộc đường thẳng 1 1 : 2 1 1 x y z sao cho biểu thức 2 2 22 3 4 P MA MB MC đạt giá trị nhỏ nhất. Tính giá trị biểu thức P a b c . A. 8 . 3 B. 3. C. 5. D. 11 . 3 Câu 201. Gọi ; ;A a b c là hình chiếu của điểm 1; 2;3M lên trục Oz . Tính S a b c . A. 3S . B. 2S . C. 1S . D. 2S . Câu 202. Viết phương trình mặt cầu tâm 1;2; 3I và có bán kính 5R . A. 2 2 2 1 2 3 5x y z . B. 2 2 2 1 2 3 25x y z . C. 2 2 2 1 2 3 5x y z . D. 2 2 2 1 2 3 5x y z . Câu 203. Một mặt phẳng có bao nhiêu véc tơ pháp tuyến. A. 1. B. 2 . C. 3 . D. Vô số. Câu 204. Phương trình nào sau đây là phương trình mặt phẳng Oxy ? A. 0x . B. 0y . C. 0x y . D. 0z . TRƯỜNG THPT LƯƠNG NGỌC QUYẾN, TỔ TOÁN-TIN 26 Câu 205. Trong không gian Oxyz , cho 2 điểm 2;1; 3 , 3; 1; 1A B . Độ dài đoạn thẳng AB là? A. 41 . B. 1 . C. 3 . D. 5 . Câu 206. Cho hai đường thẳng: 1 1 2 3 : 2 3 4 x y z d , 2 3 5 7 : 4 6 8 x y z d . Trong các mệnh đề sau, mệnh đề nào đúng? A. 1 2d d . B. 1 2//d d . C. 1 2d d . D. 1d , 2d chéo nhau. Câu 207. Trong không gian Oxyz , tọa độ điểm H là hình chiếu vuông góc của điểm 1; 1;2M lên mặt phẳng Oyz là A. 1; 1;0H . B. 0; 1;2H . C. 1;0;2H . D. 1;0;0H . Câu 208. Trong không gian Oxyz , cho mặt phẳng :4 3 1 0x y z và mặt : 2 2 1 0mx y z . Xác định tất cả các giá trị của tham số m để mặt phẳng vuông góc với mặt phẳng . A. 2m . B. 1m . C. 1m . D. 2m . Câu 209. Trong không gian Oxyz , điểm nào sau đây nằm trên mặt phẳng Oxy ? A. 1;0;2M . B. 1;2;3N . C. 1;2;0P . D. 0;0;2Q . Câu 210. Trong không gian với hệ tọa độ Oxyz . Đường thẳng 2 : 3 2 x t d y t z t đi qua điểm nào sau đây? A. 2;3; 2M . B. 2; 1;1N . C. 0; 1;1P . D. 0;3; 2Q . Câu 211. Trong không gian với hệ tọa độ Oxyz . Cho 1;2;3A và 1;0; 1I . Tìm tọa độ điểm B , biết I là trung điểm của đoạn thẳng AB . A. 2;2;2 . B. 1;1;1 . C. 1; 2; 5 . D. 1;2;5 . Câu 212. Trong không gian với hệ tọa độ Oxyz . Cho // , biết phương trình :3 7 0x z . Một vectơ pháp tuyến của là: A. 3; 1; 7n . B. 3;0; 1n . C. 3; 1;0n . D. 3; 7; 1n . Câu 213. Trong không gian tọa độ Oxyz , cho hai đường thẳng có vectơ chỉ phương lần lượt là ( ; ; ); ( ; ; )u a b c v x y z . Công thức nào sau đây là công thức đúng để tính góc giữa hai đường thẳng đã cho ? A. 2 2 2 2 2 2 z . ax by c Cos a b c x y z . B. 2 2 2 2 2 2 z . ax by c Sin a b c x y z . C. 2 2 2 2 2 2 z . ax by c Cos a b c x y z . D. 2 2 2 2 2 2 z . ax by c Sin a b c x y z . Câu 214. Trong không gian tọa độ Oxyz , chọn số phát biểu đúng trong các phát biểu sau đây. I. Một mặt phẳng có vô số vectơ pháp tuyến. TRƯỜNG THPT LƯƠNG NGỌC QUYẾN, TỔ TOÁN-TIN 27 II. Mỗi đường thẳng chỉ có đúng một vectơ chỉ phương. III. Góc giữa hai mặt phẳng là một góc nhọn IV. Hai mặt phẳng song song thì có hai vectơ pháp tuyến cùng phương. A. 4. B. 1. C. 2. D. 3. Câu 215. Trong không gian tọa độ Oxyz , Cho điểm A(-1;5;3), (0;2;3)B . Vectơ nào sau đây là vectơ chỉ phương của đường thẳng AB? A. 1;7;6u . B. ( 1;7;5)u . C. (1; 3;0)u . D. ( 1;3;1)u . Câu 216. Trong không gian Oxyz , cho đường thẳng d có phương trình chính tắc 1 2 1 3 4 yx z . Khi đó đường thẳng d có phương trình tham số là A. 1 3 2 4 x t y t z t . B. 1 3 2 4 x t y t z t . C. 1 3 4 2 x t y z t . D. 1 3 4 2 x t y z t . Câu 217. Trong các phương trình sau, phương trình nào là phương trình mặt cầu? A. 2 2 2 2 3 0 x y z x yz . B. 2 2 2 2 4 4 0 x y z x y . C. 2 2 2 4 4 2 8 0 x y z x y z . D. 2 2 2 4 2 6 0 x y z y z . Câu 218. Trong không gian Oxyz , cho 0;0;2 , 0; 1;0 , 3;0;0 .A B C Phương trình nào dưới đây là phương trình của mặt phẳng .ABC A. 1 3 1 2 x y z . B. 1 2 1 3 x y z . C. 1 1 2 3 x y z . D. 1 3 2 1 x y z . Câu 219. Trong không gian Oxyz , cho ba vectơ: (1; 2;3)a , 0; 2;2b , 1;5;3c . Tọa độ vectơ 1 4 3 2 x a b c là A. 7; 22;2x B. 1;8;20x C. 1;6;22x D. 7; 24;4x Câu 220. Cho ba điểm 2;1; 3A , 3; 4;3B và ; ; 3C x y . Với giá trị nào của ,x y thì ba điểm , ,A B C thẳng hàng ? A. 1x và 2y . B. 1x và 2y . C. 1x và 3y . D. 2x và 1y . Câu 221. Trong không gian Oxyz , phương trình nào dưới đây là phương trình đường thẳng đi qua điểm 1;2;0A và vuông góc với mặt phẳng : 2 3 5 0P x y z . A. 3 2 3 3 3 x t y t z t . B. 1 2 2 3 x t y t z t . C. 3 2 3 3 3 x t y t z t . D. 1 2 2 3 x t y t z t Câu 222. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng 1 2 1 : 1 1 2 x y z và mặt phẳng : 2 5 0P x y z . Tọa độ giao điểm A của đường thẳng và mặt phẳng P là: A. 3;0; 1 . B. 0;3;1 . C. 0;3; 1 . D. 1;0;3 . Câu 223. Trong không gian với hệ tọa độ Oxyz ,cho mặt cầu 2 2 2: ( 4) ( 1) 36S x y z . Vị trí tương đối của mặt cầu ( )S với mặt phẳng Oxy là: TRƯỜNG THPT LƯƠNG NGỌC QUYẾN, TỔ TOÁN-TIN 28 A. Oxy cắt ( )S . B. Oxy không cắt ( )S . C. Oxy tiếp xúc ( )S . D. Oxy đi qua tâm của ( )S . Câu 224. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng : 3 0x y nz và : 2 2 6 0x my z . Với giá trị nào của m , n thì (α) // β ? A. 2m và 1n . B. 1m và 1n . C. 2m và 1n . D. 2m và 1n . Câu 225. Trong không gian với hệ trục độ Oxyz , cho ba điểm 1; 2;1A , 1;3;3B , 2; 4;2C . Một véc tơ pháp tuyến n của mặt phẳng ABC là: A. ( 1;9;4)n . B. (9;4; 1)n . C. (4;9; 1)n . D. (9;4;11)n . Câu 226. Trong không gian với hệ trục Oxyz , cho ba điểm 1;2; 3 , 1;0;2 , ; ; 2A B C x y thẳng hàng. Khi đó x y bằng A. 1x y . B. 17x y . C. 11 5 x y . D. 11 5 x y . Câu 227 . Cho hai đường thẳng d : 3 1 2 2 2 x t y t z t và 'd : 1 2 2 4 4 4 x t y t z t . Mệnh đề nào dưới đây đúng? A. d và 'd cắt nhau. B. d và 'd chéo nhau. C. d và 'd trùng nhau. D. d và 'd song song. Câu 228. Cho hai đường thẳng ( )P : 2 2 2020 0x y z và ( )Q : 2 2 2022 0x y z . Khoảng cách giữa hai mặt phẳng ( )P và ( )Q là: A. 2 3 . B. 1 3 . C. 2 . D. 2 3 . Câu 229. Trong không gian ,Oxyz cho đường thẳng 3 1 2 : . 2 3 5 x y z d Mặt phẳng nào sau đây vuông góc với đường thẳng d . A. 3 2 3 0x y z . B. 3 2 3 0x y z . C. 4 6 10 1 0x y z . D. 4 6 10 1 0x y z . Câu 230. Trong không gian ,Oxyz cho mặt cầu 2 2 2: 2 4 2 3 0S x y z x y z . Một dạng khác của phương trình mặt cầu S là: A. 2 2 2 1 2 1 9x y z . B. 2 2 2 1 2 1 9x y z . C. 2 2 2 1 2 1 3x y z . D. 2 2 2 1 2 1 3x y z . Câu 231. Trong không gian với hệ trục tọa độ Oxyz , viết phương trình mặt phẳng tiếp xúc với 2 2 2: 2 4 6 2 0S x y z x y z và song song với : 4 3 12 10 0x y z . A. 4 3 12 26 0 4 3 12 78 0 x y z x y z . B. 4 3 12 26 0 4 3 12 78 0 x y z x y z . C. 4 3 12 26 0 4 3 12 78 0 x y z x y z . D. 4 3 12 26 0 4 3 12 78 0 x y z x y z . TRƯỜNG THPT LƯƠNG NGỌC QUYẾN, TỔ TOÁN-TIN 29 Câu 232. Trong không gian Oxyz , cho tứ diện ABCD có (2;1; 1), (3;0;1),C(2; 1;3)A B và D thuộc trục Oy . Biết 5ABCDV và có hai điểm 1 1 2 20; ;0 , 0; ;0D y D y thỏa mãn yêu cầu bài toán. Khi đó 1 2y y bằng A. 0 . B. 1. C. 2 . D. 3 . Câu 233. Trong không gian với hệ tọa độ Oxyz , cho hai điểm 1; 1;5M và 0;0;1N . Mặt phẳng chứa M , N và song song với trục Oy có phương trình là: A. 4 2 0x z . B. 2 3 0x z . C. 4 1 0x z . D. 4 1 0x z . Câu 234. Trong không gian với hệ tọa độ Oxyz , cho điểm 2; 6;3M và đường thẳng 1 3 : 2 2 x t d y t z t . Gọi H là hình chiếu vuông góc của M lên d . Khi đó toạ độ điểm H là: A. 1; 2;3H . B. 4; 4;1H . C. 1;2;1H . D. 8;4;3H . Câu 235: Trong không gian tọa độ Oxyz , đường thẳng d đi qua điểm 1; 2;3A và có vectơ chỉ phương 2; 1; 2u có phương trình tham số là A. 3 2 : 2 1 2 x t d y t z t . B. 2 : 1 2 2 3 x t d y t z t . C. 1 2 : 2 3 2 x t d y t z t . D. 5 2 : 4 1 2 x t d y t z t . Câu 236: Trong không gian Oxyz , cho mặt cầu 2 2 2: 4 2 2 3 0S x y z x y z và mặt phẳng : 2 2 14 0P x y z . Viết phương trình mặt phẳng Q và song song với mặt phẳng P đồng thời Q tiếp xúc với mặt cầu S . A. : 2 2 11 0Q x y z . B. : 2 2 7 0Q x y z . C. : 2 11 0Q x y z , : 2 2 7 0Q x y z . D. : 2 2 11 0Q x y z , : 2 2 4 0Q x y z . Câu 237. [Vận dụng cao] Trong không gian Oxyz , cho ba điểm 3;0;0A , 0;3;0B , 0;0;3C và đường thẳng 2 1 : 1 1 1 x y z d . Điểm M trên đường thẳng d sao cho 2 3MA MB MC đạt giá trị nhỏ nhất. Tung độ điểm M là A. 2 . B.1. C. 2 . D. 1 . Câu 238. [Vận dụng cao] Trong không gian Oxyz , cho hai điểm 1;4;1A ; 2; 1;0B và mặt phẳng : 2 1 0P x y z . Điểm M thuộc mặt phẳng P sao cho 2 22MA MB đạt giá trị nhỏ nhất. Hoành độ của điểm M là A. 11 18 . B. 19 18 . C. 11 18 . D. 19 18 . TRƯỜNG THPT LƯƠNG NGỌC QUYẾN, TỔ TOÁN-TIN 30 Câu 239. [Vận dụng cao] Trong không gian Oxyz , cho mặt phẳng P thay đổi nhưng luôn cắt tia Ox , Oy , Oz lần lượt tại ;0;0A a , 0;b;0B , 0;0;C c thỏa mãn 4 2bc ac ab abc . Khi thể tích tứ diện OABC đạt giá trị nhỏ nhất thì phương trình mặt phẳng P là A. 4 2 12 0x y z . B. 4 2 12 0x y z . C. 4 2 12 0x y z . D. 4 2 12 0x y z . Câu 240. [Vận dụng cao] Trong không gian Oxyz , cho biết đường cong C là tập hợp tâm của các mặt cầu đi qua 1;2;3A đồng thời tiếp xúc với mặt phẳng : 9 0x y z và mặt phẳng : 9 0x y z . Diện tích hình phẳng giới hạn bởi đường cong C bằng A. 96 . B. 48 . C. 120 . D. 60 .
File đính kèm:
 de_cuong_on_tap_kiem_tra_hoc_ky_ii_mon_toan_lop_12_nam_hoc_2.pdf
de_cuong_on_tap_kiem_tra_hoc_ky_ii_mon_toan_lop_12_nam_hoc_2.pdf

