Đánh giá giải pháp giảm nhiễu cho tín hiệu tiếng nói sử dụng các phép biến đổi Wavelet

nh hai thành phần: 
nhiễu với bộ lọc phần trăm PF [6]. Trong miền Wavelet, thành phần xấp xỉ A “tương ứng với thành phần tần số 
tín hiệu tiếng nói được phân tích thành các sóng con, ứng thấp” và thành phần chi tiết D “tương ứng thành phần tần 
với mỗi hệ số Wavelet đóng góp vào mức nhiễu với số cao” thông qua hai bộ lọc thông thấp và thông cao, trong 
phương sai 휎2 cho phép xác định chính xác các hệ số nhiễu. đó, bộ lọc thông cao sử dụng hàm Wavelet Ψ(x) và bộ lọc 
Kết quả thực hiện sẽ được so sánh, đánh giá với các kỹ thông thấp sử dụng hàm tỉ lệ (scaling function) Φ(x). 
thuật đã đề xuất cho thấy rằng, các hàm nén nhiễu trong Mối quan hệ giữa hàm tỉ lệ và hàm Wavelet được cho 
miền Wavelet tỏ ra khá hiệu quả với các loại nhiễu khác bởi: 
nhau trong môi trường thực. N−1
 Φ(x) = ∑k=0 ck. Φ(2x − k) (4) 
2. Phép biến đổi Wavelet N−1 k
 Ψ(x) = ∑k=0 (−1) ck. Φ(2x + k − N + 1) (5) 
 Gọi f(x) là tín hiệu ban đầu, phép biến đổi Wavelet của 
 Trong đó, Ψ(x) là hàm tỉ lệ cho hàm Wavelet Φ và ck
f(x) sử dụng hàm Wavelet ψ0 được biểu diễn [5]: là các hệ số Wavelet. 
2 Dương Ngọc Pháp, Võ Thị Diệu Hạnh 
3. Mô hình nhiễu cộng trong miền Wavelet 
 ,푖 = 휎 ,푖 √2푙표 ,푖 (8) 
 Do tính chất tuyến tính của biến đổi Wavelet rời rạc 1
 Trong đó, 휎 = 푒 푖 푛(|푌 (푛)|) là ước 
DWT (Discrete Wavelet Transform), mô hình nhiễu cộng ,푖 0.6745 ,푖
trong miền tần số cũng đúng trong miền Wavelet [7]: lượng bền vững của độ lệch chuẩn bằng cách tính Median 
 Absolute Deviation (MAD) của chuỗi các hệ số. 
 ( ) ( ) ( )
 푌 ,푖 푛 = ,푖 푛 + ,푖 푛 (6) 5. Thuật toán giảm nhiễu trong miền Wavelet 
trong đó, 푌 ,푖(푛), ,푖(푛) và ,푖(푛) mô tả các chuỗi hệ 5.1. Kỹ thuật nén nhiễu ngưỡng cứng và ngưỡng mềm 
số gói Wavelet của các tín hiệu bị nhiễu, tín hiệu sạch và Kỹ thuật khử nhiễu trong miền Wavelet xuất phát từ 
tín hiệu nhiễu tương ứng được tính tại tỷ lệ thứ m cho frame 
 m nguyên tắc: Mỗi hệ số Wavelet đóng góp vào mức nhiễu 
thứ i (k = 1, 2, 3, 2 ). với phương sai là 휎2, nhưng chỉ có một vài số hệ số 
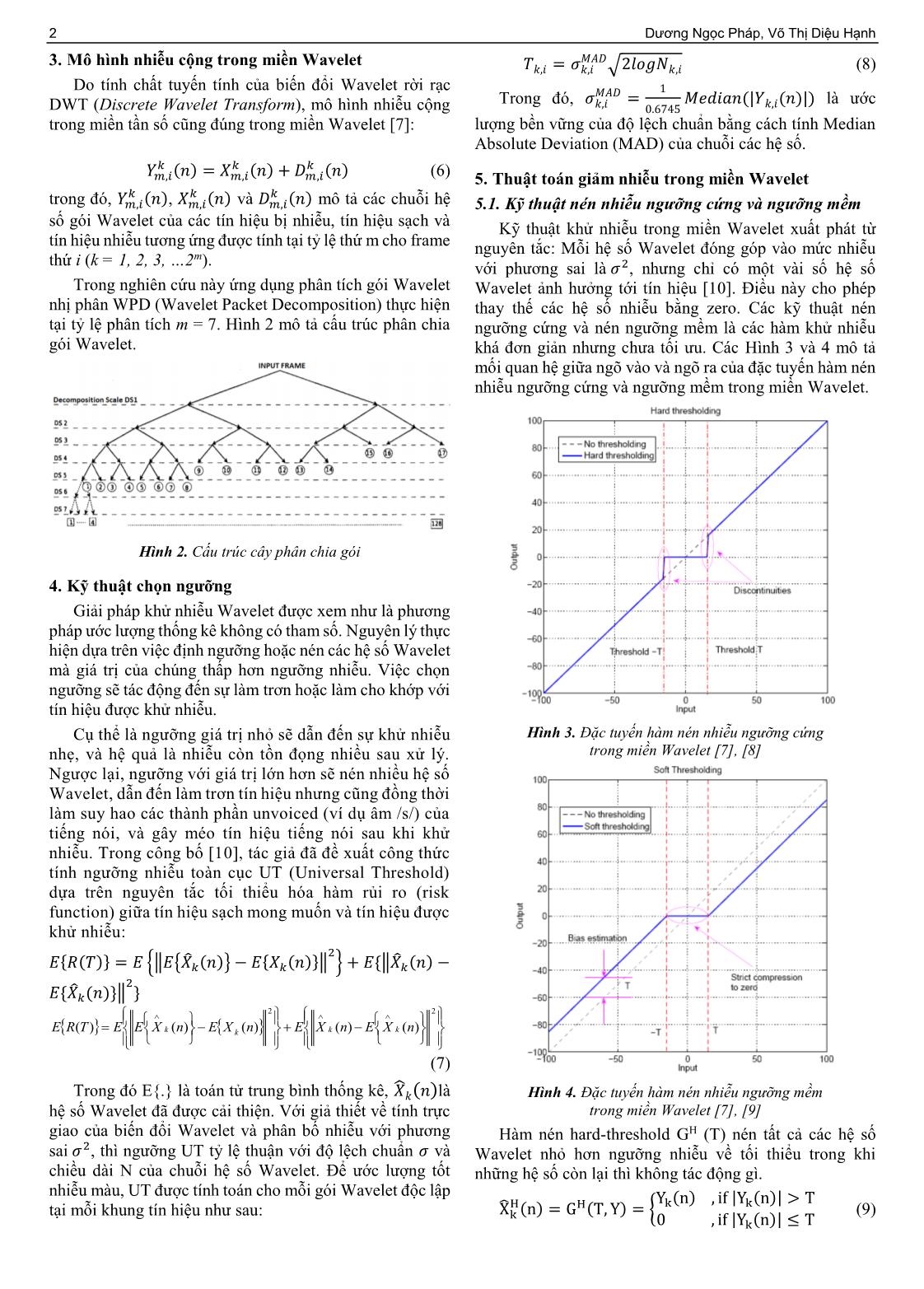
 Trong nghiên cứu này ứng dụng phân tích gói Wavelet Wavelet ảnh hưởng tới tín hiệu [10]. Điều này cho phép 
nhị phân WPD (Wavelet Packet Decomposition) thực hiện thay thế các hệ số nhiễu bằng zero. Các kỹ thuật nén 
tại tỷ lệ phân tích m = 7. Hình 2 mô tả cấu trúc phân chia ngưỡng cứng và nén ngưỡng mềm là các hàm khử nhiễu 
gói Wavelet. khá đơn giản nhưng chưa tối ưu. Các Hình 3 và 4 mô tả 
 mối quan hệ giữa ngõ vào và ngõ ra của đặc tuyến hàm nén 
 nhiễu ngưỡng cứng và ngưỡng mềm trong miền Wavelet. 
 Hình 2. Cấu trúc cây phân chia gói 
4. Kỹ thuật chọn ngưỡng 
 Giải pháp khử nhiễu Wavelet được xem như là phương 
pháp ước lượng thống kê không có tham số. Nguyên lý thực 
hiện dựa trên việc định ngưỡng hoặc nén các hệ số Wavelet 
mà giá trị của chúng thấp hơn ngưỡng nhiễu. Việc chọn 
ngưỡng sẽ tác động đến sự làm trơn hoặc làm cho khớp với 
tín hiệu được khử nhiễu. 
 Cụ thể là ngưỡng giá trị nhỏ sẽ dẫn đến sự khử nhiễu Hình 3. Đặc tuyến hàm nén nhiễu ngưỡng cứng 
nhẹ, và hệ quả là nhiễu còn tồn đọng nhiều sau xử lý. trong miền Wavelet [7], [8] 
Ngược lại, ngưỡng với giá trị lớn hơn sẽ nén nhiều hệ số 
Wavelet, dẫn đến làm trơn tín hiệu nhưng cũng đồng thời 
làm suy hao các thành phần unvoiced (ví dụ âm /s/) của 
tiếng nói, và gây méo tín hiệu tiếng nói sau khi khử 
nhiễu. Trong công bố [10], tác giả đã đề xuất công thức 
tính ngưỡng nhiễu toàn cục UT (Universal Threshold) 
dựa trên nguyên tắc tối thiểu hóa hàm rủi ro (risk 
function) giữa tín hiệu sạch mong muốn và tín hiệu được 
khử nhiễu: 
 2
 {푅( )} = {‖ { ̂ (푛)} − { (푛)}‖ } + {‖ ̂ (푛) −
 2
 { ̂ (푛)}‖ }
 2 2
       
 E R(T) E E X k (n) E X k (n)  E X k (n) E X k (n) 
     
 (7) 
 Trong đó E{.} là toán tử trung bình thống kê, ̂ (푛)là Hình 4. Đặc tuyến hàm nén nhiễu ngưỡng mềm 
hệ số Wavelet đã được cải thiện. Với giả thiết về tính trực trong miền Wavelet [7], [9] 
giao của biến đổi Wavelet và phân bố nhiễu với phương Hàm nén hard-threshold GH (T) nén tất cả các hệ số 
sai 휎2, thì ngưỡng UT tỷ lệ thuận với độ lệch chuẩn 휎 và Wavelet nhỏ hơn ngưỡng nhiễu về tối thiểu trong khi 
chiều dài N của chuỗi hệ số Wavelet. Để ước lượng tốt những hệ số còn lại thì không tác động gì. 
nhiễu màu, UT được tính toán cho mỗi gói Wavelet độc lập ( ) | ( )|
 ̂H H Yk n , if Yk n > T
tại mỗi khung tín hiệu như sau: Xk (n) = G (T, Y) = { (9) 
 0 , if |Yk(n)| ≤ T
ISSN 1859-1531 - TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ ĐẠI HỌC ĐÀ NẴNG, SỐ 05(114).2017-Quyển 2 3 
 Với hàm nén ngưỡng mềm được đề xuất trong [9], 1, 푖 훾 ,푖 < 1
những điểm gián đoạn trong đặc tuyến ngõ ra của hàm nén 훾 ,푖
 ,푖 = { (1+휇 ,푖) −1
ngưỡng cứng được loại bỏ bằng cách nén các hệ số Wavelet 푠 푛 {푌 ,푖( ) } , 푖 훾 ,푖 < 1
hơn mức ngưỡng 1 giá trị, bằng chính giá trị ngưỡng T 휇 ,푖훾 ,푖
được ước lượng: ,1 if  k, i 1
 푆 푆 
 ̂ (푛) = ( , 푌) = k, i
 H k, i (1 k, i ) 1
 푠 푛(푌 (푛))(|푌 (푛)| − ) , 푖 |푌 (푛)| > sgn Y ( p )  ,if  1
{ (10) k, i   k, i
 0 , 푖 |푌 (푛)| ≤ k,, i k i
 Hàm nén ngưỡng mềm dù đã cải thiện nhưng vẫn chưa (11) 
đạt tối ưu vì quy luật nén tuyệt đối các hệ số dưới ngưỡng 
 |푌 ,푖( )|
về 0, nó có thể phá hủy những hệ số Wavelet của tín hiệu Ở đây, 훾 ,푖 ≜ và thông số thích nghi 휇 ,푖 được
 훤 ,푖
tiếng nói vô thanh, do sự tương tự của tiếng nói vô thanh định nghĩa [1]: 
và một số mức nhiễu. Hàm nén ngưỡng cứng dẫn đến 
 ̃ max{|푌 ,푖( )|}
phương sai lớn hơn vì tính chất không liên tục của hàm 훤 ,푖 
 휇 ,푖 = exp (훽 )
 max{훤̃ ,푖} 훤̃ ,푖
gain, trong khi ngưỡng mềm thì dẫn đến mức độ dịch 푖
chuyển lớn hơn, do tất cả những hệ số nào lớn hơn ngưỡng 
 ~ max |Y ( p ) | 
đều giảm đi một lượng bằng giá trị ngưỡng T. k, i k, i
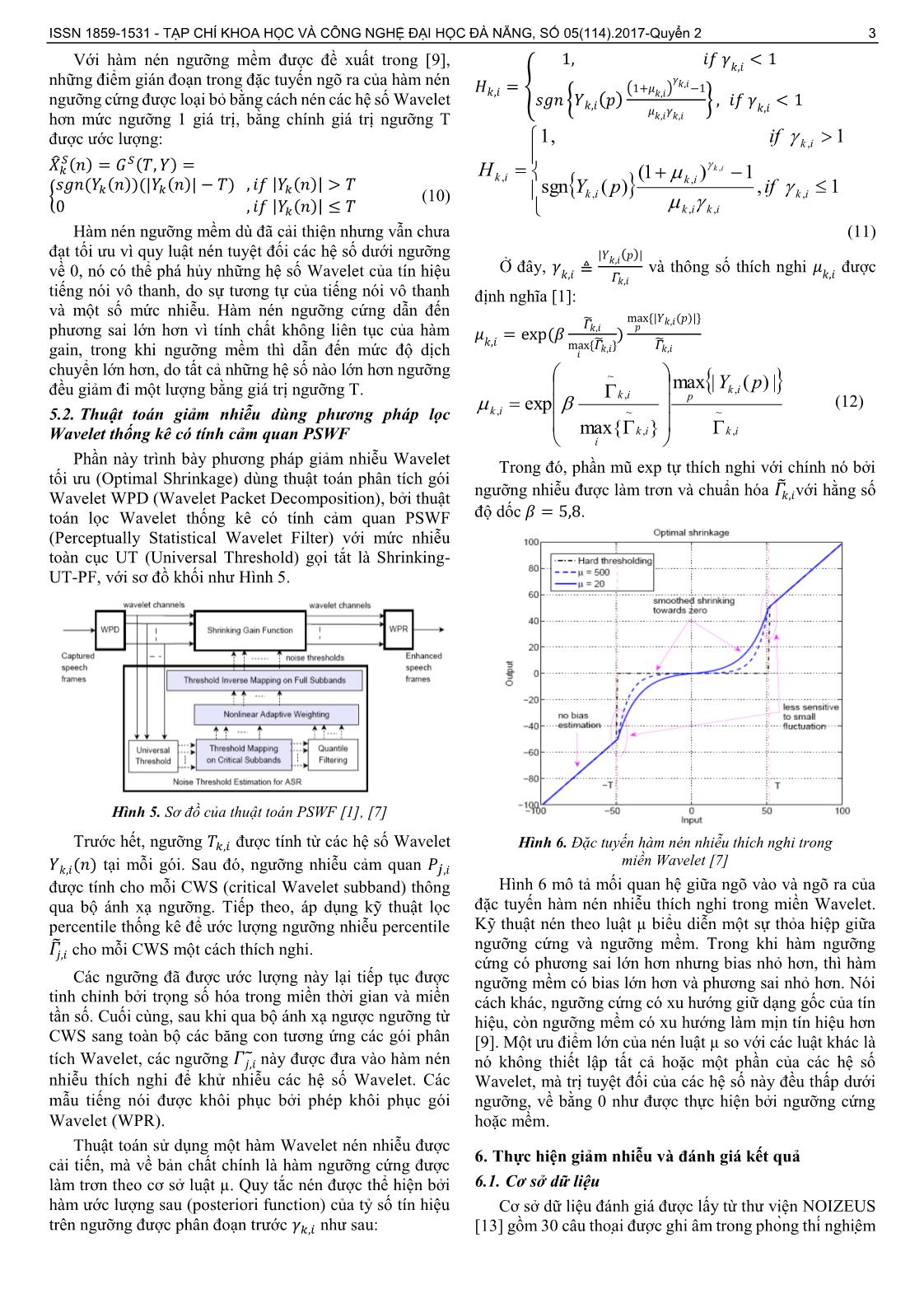
  exp  p (12) 
5.2. Thuật toán giảm nhiễu dùng phương pháp lọc k, i ~ ~
Wavelet thống kê có tính cảm quan PSWF max{k, i } k, i
 i 
 Phần này trình bày phương pháp giảm nhiễu Wavelet Trong đó, phần mũ exp tự thích nghi với chính nó bởi 
tối ưu (Optimal Shrinkage) dùng thuật toán phân tích gói ̃
Wavelet WPD (Wavelet Packet Decomposition), bởi thuật ngưỡng nhiễu được làm trơn và chuẩn hóa 훤 ,푖với hằng số 
toán lọc Wavelet thống kê có tính cảm quan PSWF độ dốc 훽 = 5,8. 
(Perceptually Statistical Wavelet Filter) với mức nhiễu 
toàn cục UT (Universal Threshold) gọi tắt là Shrinking-
UT-PF, với sơ đồ khối như Hình 5. 
 Hình 5. Sơ đồ của thuật toán PSWF [1], [7] 
 Trước hết, ngưỡng ,푖 được tính từ các hệ số Wavelet Hình 6. Đặc tuyến hàm nén nhiễu thích nghi trong 
 miền Wavelet [7] 
푌 ,푖(푛) tại mỗi gói. Sau đó, ngưỡng nhiễu cảm quan 푃푗,푖
được tính cho mỗi CWS (critical Wavelet subband) thông Hình 6 mô tả mối quan hệ giữa ngõ vào và ngõ ra của 
qua bộ ánh xạ ngưỡng. Tiếp theo, áp dụng kỹ thuật lọc đặc tuyến hàm nén nhiễu thích nghi trong miền Wavelet. 
percentile thống kê để ước lượng ngưỡng nhiễu percentile Kỹ thuật nén theo luật µ biểu diễn một sự thỏa hiệp giữa 
훤̃ cho mỗi CWS một cách thích nghi. ngưỡng cứng và ngưỡng mềm. Trong khi hàm ngưỡng 
 푗,푖 cứng có phương sai lớn hơn nhưng bias nhỏ hơn, thì hàm 
 Các ngưỡng đã được ước lượng này lại tiếp tục được ngưỡng mềm có bias lớn hơn và phương sai nhỏ hơn. Nói 
tinh chỉnh bởi trọng số hóa trong miền thời gian và miền cách khác, ngưỡng cứng có xu hướng giữ dạng gốc của tín 
tần số. Cuối cùng, sau khi qua bộ ánh xạ ngược ngưỡng từ hiệu, còn ngưỡng mềm có xu hướng làm mịn tín hiệu hơn 
CWS sang toàn bộ các băng con tương ứng các gói phân [9]. Một ưu điểm lớn của nén luật µ so với các luật khác là 
tích Wavelet, các ngưỡng 훤̃푗,푖 này được đưa vào hàm nén nó không thiết lập tất cả hoặc một phần của các hệ số 
nhiễu thích nghi để khử nhiễu các hệ số Wavelet. Các Wavelet, mà trị tuyệt đối của các hệ số này đều thấp dưới 
mẫu tiếng nói được khôi phục bởi phép khôi phục gói ngưỡng, về bằng 0 như được thực hiện bởi ngưỡng cứng 
Wavelet (WPR). hoặc mềm. 
 Thuật toán sử dụng một hàm Wavelet nén nhiễu được 
 6. Thực hiện giảm nhiễu và đánh giá kết quả
cải tiến, mà về bản chất chính là hàm ngưỡng cứng được 
làm trơn theo cơ sở luật µ. Quy tắc nén được thể hiện bởi 6.1. Cơ sở dữ liệu 
hàm ước lượng sau (posteriori function) của tỷ số tín hiệu Cơ sở dữ liệu đánh giá được lấy từ thư viện NOIZEUS 
trên ngưỡng được phân đoạn trước 훾 ,푖 như sau: [13] gồm 30 câu thoại được ghi âm trong phòng thí nghiệm 
4 Dương Ngọc Pháp, Võ Thị Diệu Hạnh 
theo chuẩn của IEEE là tín hiệu thoại sạch. Mỗi câu dài 6.3.3. Đánh giá theo phương pháp WSS 
trung bình khoảng 2 s. 
 Năm loại nhiễu được chọn để nghiên cứu là nhiễu ô tô 
(Car), nhiễu đám đông (Babble), nhiễu trắng (White), 
nhiễu từ tàu hỏa (Train) và nhiễu đường phố (Street). 
6.2. Tiêu chí đánh giá 
 Các phương pháp đánh giá khách quan được khảo sát 
để thực hiện đánh giá chất lượng tín hiệu tiếng nói qua các 
tiêu chí đánh giá, bao gồm: 
 - Segmental Signal-to-Noise Ratio (SegSNR); 
 - Log Likelihood Ratio (LLR); 
 - Cepstrum Distance (CEP); Hình 9. Kết quả đánh giá WSS của 6 thuật toán tăng cường chất 
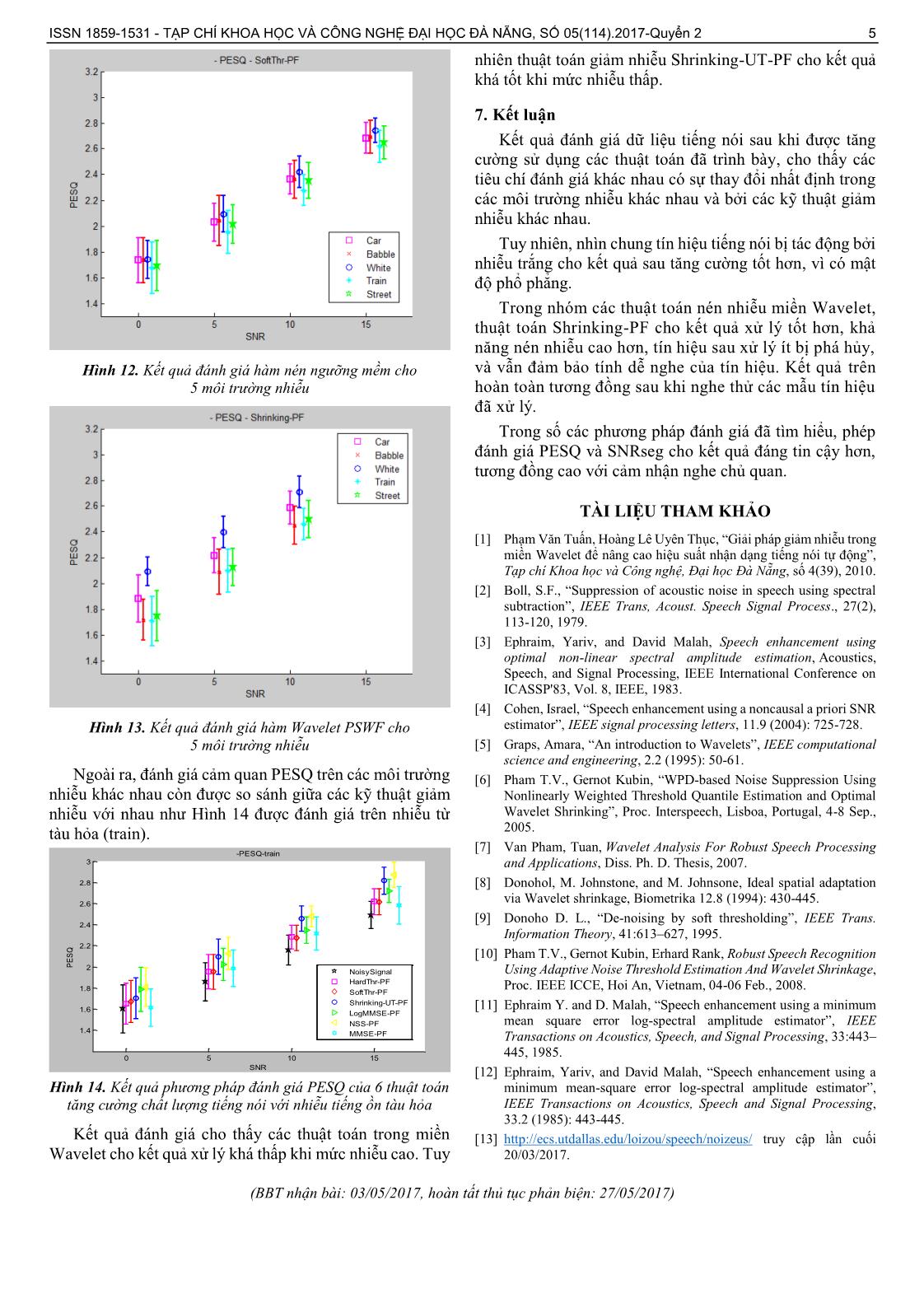
 lượng tiếng nói với loại nhiễu tiếng ồn đám đông (Babble) 
 - Perceptual Evaluation of Speech Quanlity (PESQ); 
 - Weighted Spectral Slope (WSS). 6.3.4. Đánh giá theo phương pháp SegSNR 
6.3. Kết quả đánh giá và phân tích 
 Bài báo sẽ thực hiện đánh giá, so sánh 3 kỹ thuật đã 
nghiên cứu là NSS-PF, MMSE-PF và LogMMSE-PF ước 
lượng nhiễu sử dụng bộ lọc phần trăm (PF) với 3 kỹ thuật 
giảm nhiễu trong miền Wavelet là HardThr-PF, SoftThr-
PF, Shriking-UT-PF. 
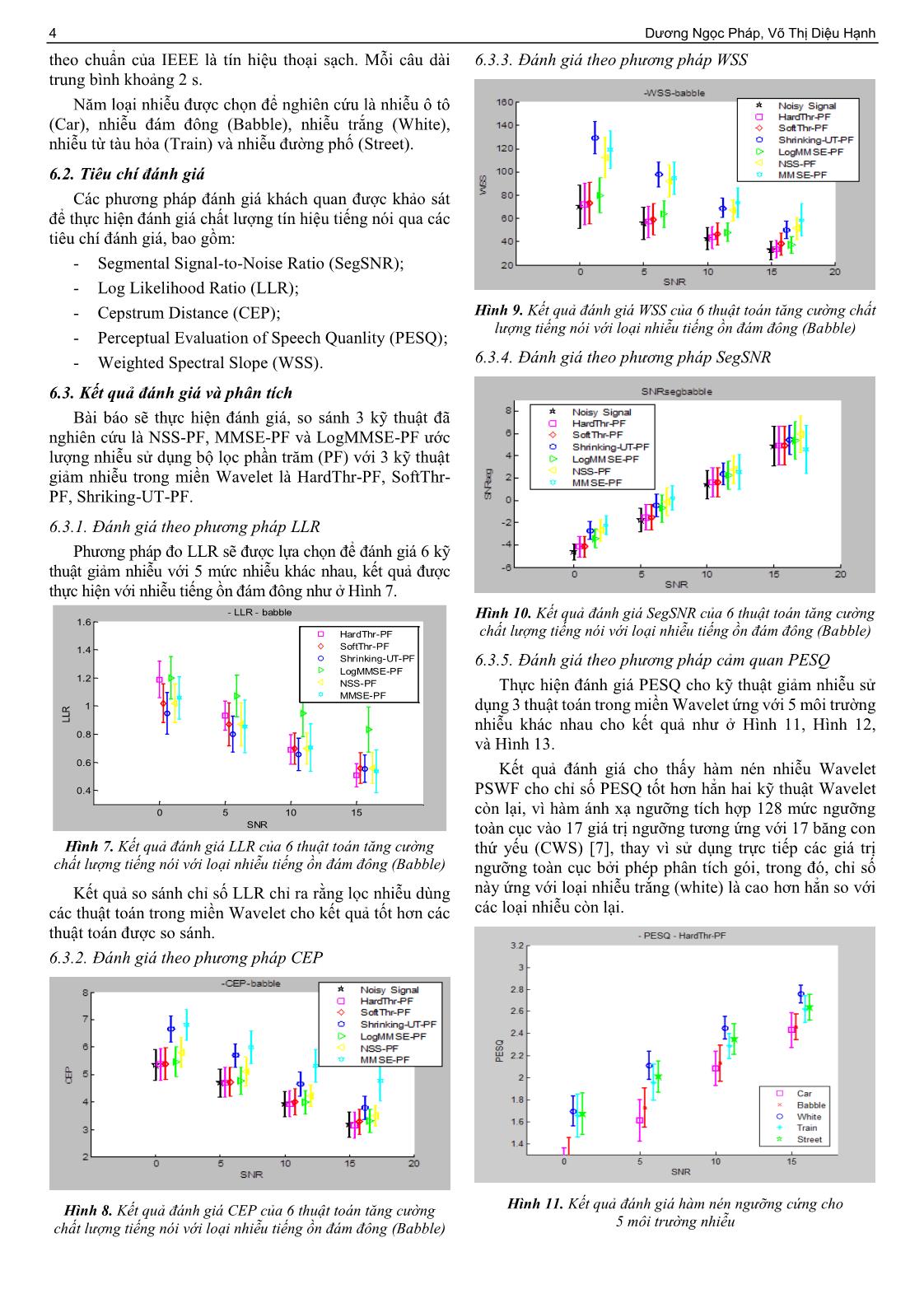
6.3.1. Đánh giá theo phương pháp LLR 
 Phương pháp đo LLR sẽ được lựa chọn để đánh giá 6 kỹ 
thuật giảm nhiễu với 5 mức nhiễu khác nhau, kết quả được 
thực hiện với nhiễu tiếng ồn đám đông như ở Hình 7. 
 - LLR - babble Hình 10. Kết quả đánh giá SegSNR của 6 thuật toán tăng cường 
 1.6
 HardThr-PF chất lượng tiếng nói với loại nhiễu tiếng ồn đám đông (Babble) 
 1.4 SoftThr-PF
 Shrinking-UT-PF 6.3.5. Đánh giá theo phương pháp cảm quan PESQ 
 LogMMSE-PF
 1.2
 NSS-PF Thực hiện đánh giá PESQ cho kỹ thuật giảm nhiễu sử 
 MMSE-PF
 1 dụng 3 thuật toán trong miền Wavelet ứng với 5 môi trường 
 LLR nhiễu khác nhau cho kết quả như ở Hình 11, Hình 12, 
 0.8
 và Hình 13. 
 0.6 Kết quả đánh giá cho thấy hàm nén nhiễu Wavelet 
 0.4 PSWF cho chỉ số PESQ tốt hơn hẳn hai kỹ thuật Wavelet 
 0 5 10 15 còn lại, vì hàm ánh xạ ngưỡng tích hợp 128 mức ngưỡng 
 SNR toàn cục vào 17 giá trị ngưỡng tương ứng với 17 băng con 
 Hình 7. Kết quả đánh giá LLR của 6 thuật toán tăng cường thứ yếu (CWS) [7], thay vì sử dụng trực tiếp các giá trị 
 chất lượng tiếng nói với loại nhiễu tiếng ồn đám đông (Babble) ngưỡng toàn cục bởi phép phân tích gói, trong đó, chỉ số 
 Kết quả so sánh chỉ số LLR chỉ ra rằng lọc nhiễu dùng này ứng với loại nhiễu trắng (white) là cao hơn hẳn so với 
các thuật toán trong miền Wavelet cho kết quả tốt hơn các các loại nhiễu còn lại. 
thuật toán được so sánh. 
6.3.2. Đánh giá theo phương pháp CEP 
 Hình 8. Kết quả đánh giá CEP của 6 thuật toán tăng cường Hình 11. Kết quả đánh giá hàm nén ngưỡng cứng cho 
 chất lượng tiếng nói với loại nhiễu tiếng ồn đám đông (Babble) 5 môi trường nhiễu 
ISSN 1859-1531 - TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ ĐẠI HỌC ĐÀ NẴNG, SỐ 05(114).2017-Quyển 2 5 
 nhiên thuật toán giảm nhiễu Shrinking-UT-PF cho kết quả 
 khá tốt khi mức nhiễu thấp. 
 7. Kết luận
 Kết quả đánh giá dữ liệu tiếng nói sau khi được tăng 
 cường sử dụng các thuật toán đã trình bày, cho thấy các 
 tiêu chí đánh giá khác nhau có sự thay đổi nhất định trong 
 các môi trường nhiễu khác nhau và bởi các kỹ thuật giảm 
 nhiễu khác nhau. 
 Tuy nhiên, nhìn chung tín hiệu tiếng nói bị tác động bởi 
 nhiễu trắng cho kết quả sau tăng cường tốt hơn, vì có mật 
 độ phổ phẳng. 
 Trong nhóm các thuật toán nén nhiễu miền Wavelet, 
 thuật toán Shrinking-PF cho kết quả xử lý tốt hơn, khả 
 năng nén nhiễu cao hơn, tín hiệu sau xử lý ít bị phá hủy, 
 Hình 12. Kết quả đánh giá hàm nén ngưỡng mềm cho và vẫn đảm bảo tính dễ nghe của tín hiệu. Kết quả trên 
 5 môi trường nhiễu hoàn toàn tương đồng sau khi nghe thử các mẫu tín hiệu 
 đã xử lý. 
 Trong số các phương pháp đánh giá đã tìm hiểu, phép 
 đánh giá PESQ và SNRseg cho kết quả đáng tin cậy hơn, 
 tương đồng cao với cảm nhận nghe chủ quan. 
 TÀI LIỆU THAM KHẢO 
 [1] Phạm Văn Tuấn, Hoàng Lê Uyên Thục, “Giải pháp giảm nhiễu trong 
 miền Wavelet để nâng cao hiệu suất nhận dạng tiếng nói tự động”, 
 Tạp chí Khoa học và Công nghệ, Đại học Đà Nẵng, số 4(39), 2010. 
 [2] Boll, S.F., “Suppression of acoustic noise in speech using spectral 
 subtraction”, IEEE Trans, Acoust. Speech Signal Process., 27(2), 
 113-120, 1979. 
 [3] Ephraim, Yariv, and David Malah, Speech enhancement using 
 optimal non-linear spectral amplitude estimation, Acoustics, 
 Speech, and Signal Processing, IEEE International Conference on 
 ICASSP'83, Vol. 8, IEEE, 1983. 
 [4] Cohen, Israel, “Speech enhancement using a noncausal a priori SNR 
 Hình 13. Kết quả đánh giá hàm Wavelet PSWF cho estimator”, IEEE signal processing letters, 11.9 (2004): 725-728. 
 5 môi trường nhiễu [5] Graps, Amara, “An introduction to Wavelets”, IEEE computational 
 science and engineering, 2.2 (1995): 50-61. 
 Ngoài ra, đánh giá cảm quan PESQ trên các môi trường [6] Pham T.V., Gernot Kubin, “WPD-based Noise Suppression Using 
nhiễu khác nhau còn được so sánh giữa các kỹ thuật giảm Nonlinearly Weighted Threshold Quantile Estimation and Optimal 
nhiễu với nhau như Hình 14 được đánh giá trên nhiễu từ Wavelet Shrinking”, Proc. Interspeech, Lisboa, Portugal, 4-8 Sep., 
tàu hỏa (train). 2005. 
 -PESQ-train [7] Van Pham, Tuan, Wavelet Analysis For Robust Speech Processing 
 3 and Applications, Diss. Ph. D. Thesis, 2007. 
 2.8 [8] Donohol, M. Johnstone, and M. Johnsone, Ideal spatial adaptation 
 2.6 via Wavelet shrinkage, Biometrika 12.8 (1994): 430-445. 
 2.4 [9] Donoho D. L., “De-noising by soft thresholding”, IEEE Trans. 
 Information Theory, 41:613–627, 1995. 
 2.2
 [10] Pham T.V., Gernot Kubin, Erhard Rank, Robust Speech Recognition 
 PESQ 2
 NoisySignal Using Adaptive Noise Threshold Estimation And Wavelet Shrinkage, 
 HardThr-PF
 1.8 Proc. IEEE ICCE, Hoi An, Vietnam, 04-06 Feb., 2008. 
 SoftThr-PF
 Shrinking-UT-PF
 1.6 [11] Ephraim Y. and D. Malah, “Speech enhancement using a minimum 
 LogMMSE-PF
 NSS-PF mean square error log-spectral amplitude estimator”, IEEE 
 1.4 MMSE-PF Transactions on Acoustics, Speech, and Signal Processing, 33:443–
 0 5 10 15 445, 1985. 
 SNR [12] Ephraim, Yariv, and David Malah, “Speech enhancement using a 
Hình 14. Kết quả phương pháp đánh giá PESQ của 6 thuật toán minimum mean-square error log-spectral amplitude estimator”, 
 tăng cường chất lượng tiếng nói với nhiễu tiếng ồn tàu hỏa IEEE Transactions on Acoustics, Speech and Signal Processing, 
 33.2 (1985): 443-445. 
 Kết quả đánh giá cho thấy các thuật toán trong miền [13]  truy cập lần cuối 
Wavelet cho kết quả xử lý khá thấp khi mức nhiễu cao. Tuy 20/03/2017. 
 (BBT nhận bài: 03/05/2017, hoàn tất thủ tục phản biện: 27/05/2017)