Combined power ratio calculation, hadamard transform and lms - Based calibration of channel mismatches in time - interleaved adcs

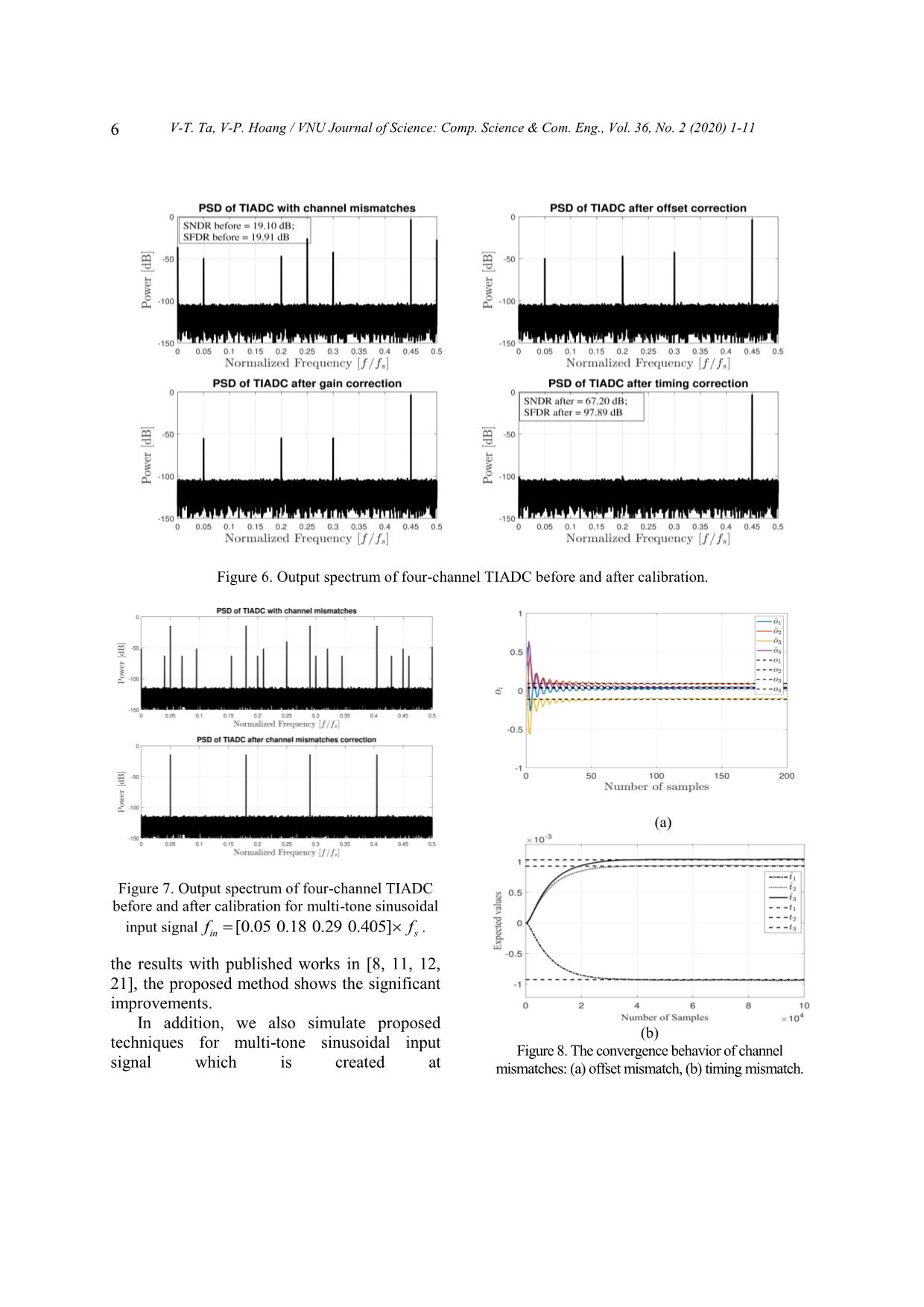
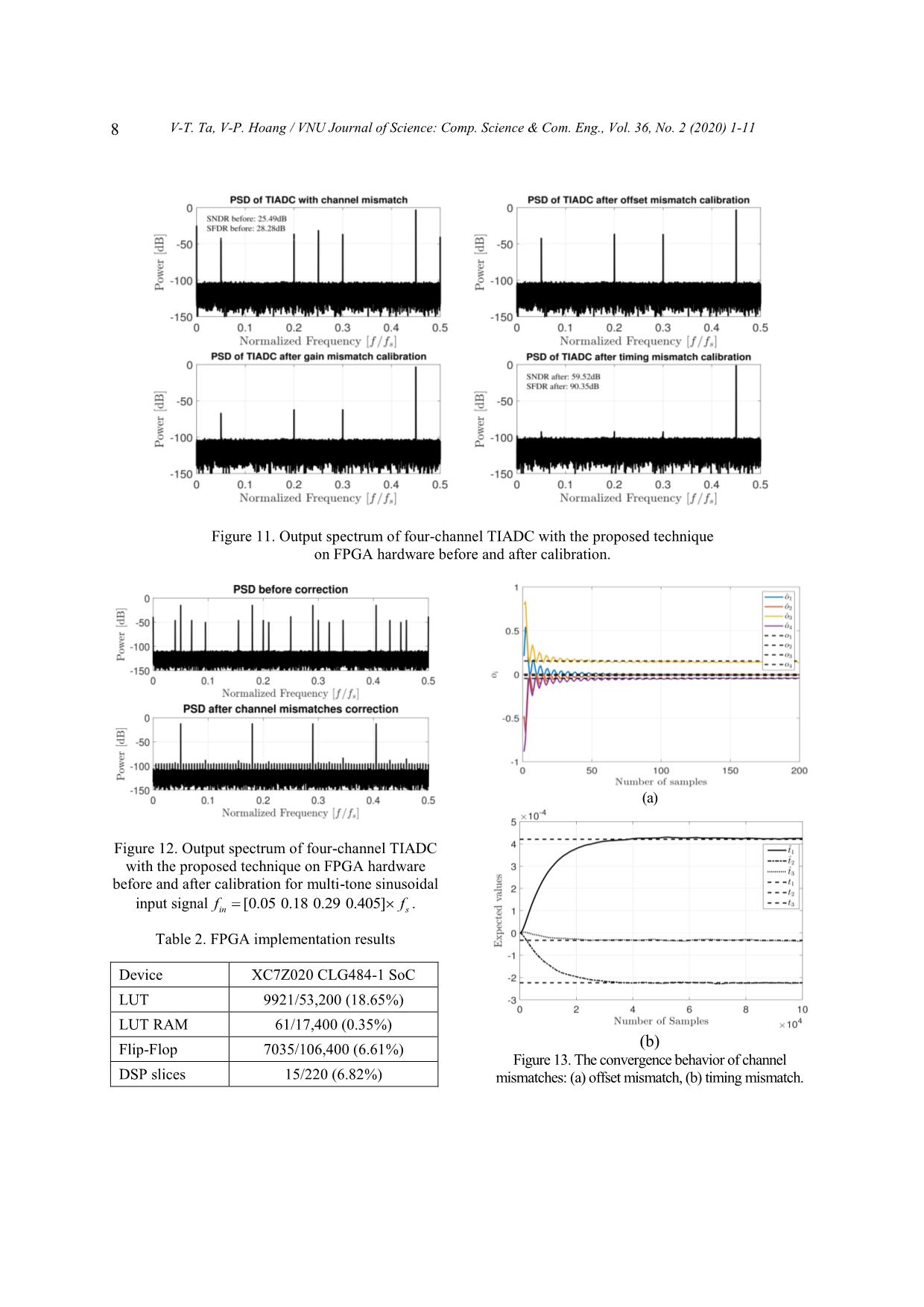
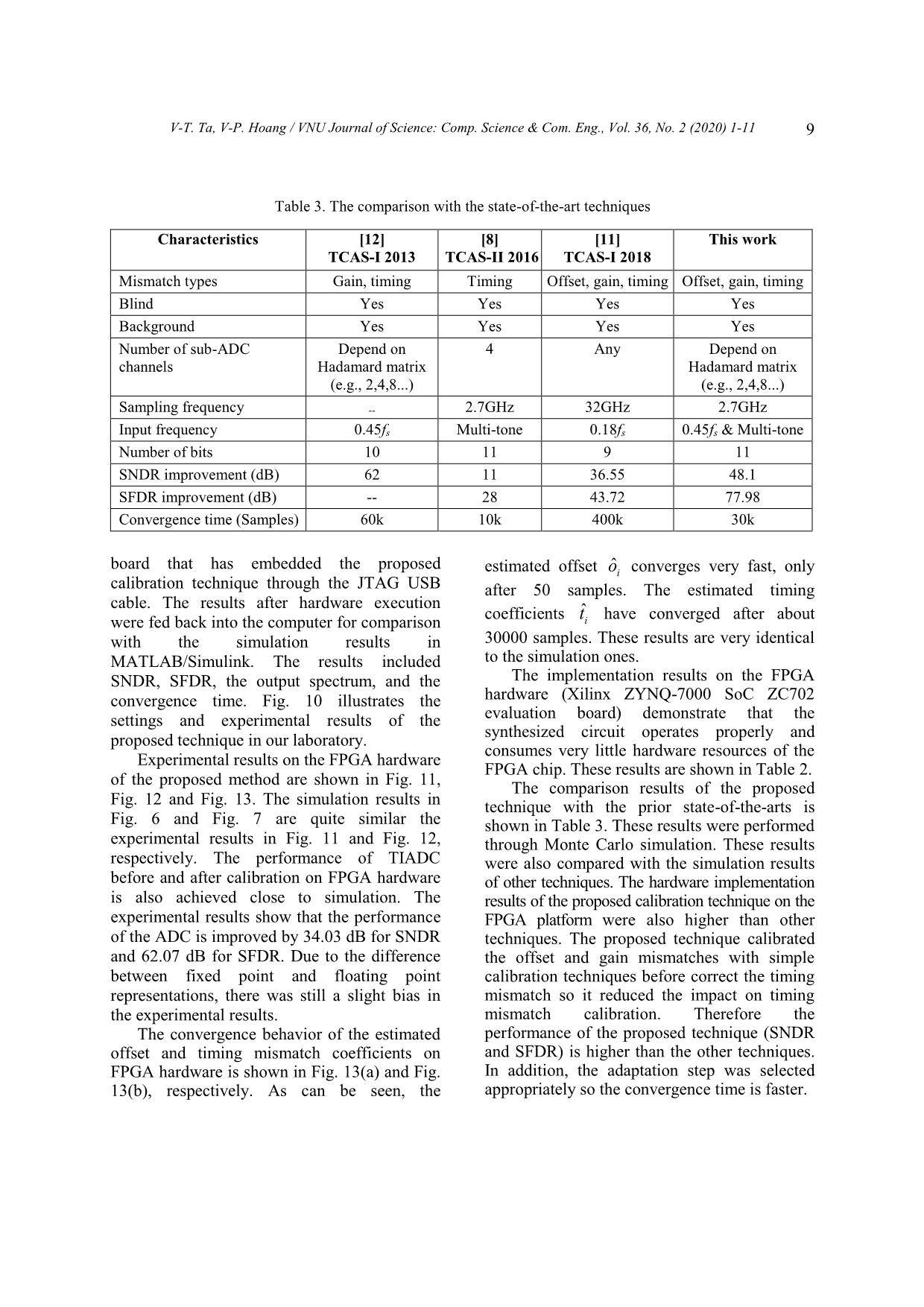
el estimation. Thus, the circuit area 
is reduced. 
 [ ] [ ]H[ ]* [ ]* [ ].dy n h n f n ty n n (15) 
Timing mismatch coefficients iˆt can be 
calculated from an updating of the correlation 
by the LMS algorithm as follows: 
  ˆ ˆ ,n  i i[n] [n -1 y [n]t t ] (16) 
where  is the step-size parameter for LMS 
algorithm, whereas [ ]n are delayed versions 
of [ ]y n after the high-pass filter [ ]f n . 
Figure 5. The timing mismatch estimation block. 
4. Experimental Results 
4.1. Simulation Results 
MATLAB software was used for simulation 
to demonstrate the efficiency of the proposed 
technique. A 33-tap correction FIR filter, 12-bit 
ADC quantization, and a sampling frequency of 
2.7GHz are used. The correction FIR filter is 
designed with the Hanning window for 
truncation and delay. The simulated results of a 
four-channel TIADC are shown, assuming that 
the channel 0 without timing mismatch is the 
reference channel for timing mismatch 
calibration, as demonstrated in Table 1. The 
input signal is bandlimited with a variance 
1 and 182 sample, LMS algorithm with 
adaptive step 
142 . The signal-to-noise 
ratio (SNR) is calculated according to equation 
(17), (18) for [ ]y n and ˆ[ ]y n as [13]: 
1
2
0
10 1
2
0
[ ]
[ ]
,10lo
[ ]
g
N
n
y N
n
x
S
n
nx y n
NR


 (17) 
1
2
0
ˆ 10 1
2
0
[ ]
[ ]
.0
[
1 og
]
l
ˆ
N
n
y N
n
x n
S
nx y n
NR


 (18) 
The simulation results in Fig. 6 show the 
output spectrum before and after channel 
mismatches calibration for single-tone 
sinusoidal input signal which is created at 
0.45in sf f . The proposed technique has 
completely eliminated all channel mismatches. 
The signal-to-noise-and-distortion ratio 
(SNDR) after calibration is 67.2 dB which leads 
to an improvement of 48.10 dB compared with 
the uncompensated output. Moreover, SFDR 
after calibration is 97.89 dB equivalent to an 
improvement of 77.98 dB compared with the 
uncompensated output. Thus, the performance 
of TIADC is significantly improved. Comparing 
Table 1. The table of channel mismatch values 
Sub 
ADC 
Channel mismatches 
oi gi ti 
ADC0 0.026883 0.0365 0 
ADC1 0.091694 -0.00481 -0.00092685Ts 
ADC2 -0.01129 -0.0047 -0.00092685Ts 
ADC3 0.043109 -0.00782 0.00092685Ts 
V-T. Ta, V-P. Hoang / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 36, No. 2 (2020) 1-11 
6 
Figure 6. Output spectrum of four-channel TIADC before and after calibration. 
Figure 7. Output spectrum of four-channel TIADC 
before and after calibration for multi-tone sinusoidal 
input signal [0.05 0.18 0.29 0.405]in sf f . 
the results with published works in [8, 11, 12, 
21], the proposed method shows the significant 
improvements. 
In addition, we also simulate proposed 
techniques for multi-tone sinusoidal input 
signal which is created at 
(a) 
(b) 
Figure 8. The convergence behavior of channel 
mismatches: (a) offset mismatch, (b) timing mismatch. 
V-T. Ta, V-P. Hoang / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 36, No. 2 (2020) 1-11 
7 
[0.05 0.18 0.29 0.405]in sf f in the 
first Nyquist band. The output spectrum of 
TIADC before and after channel mismatches 
calibration is shown in Fig. 7. As can be seen, 
the spurs due to channel mismatches 
encompassing offset, gain and timing skew are 
completely removed. 
Fig. 8(a) and Fig. (b) shows the 
convergences of correlation output ˆio and iˆt 
for offset mismatches and timing mismatches. 
As can be seen, after 25 samples, the offset 
coefficients ˆio has converged as in Fig. 8(a). 
The convergence behavior of the estimated 
timing coefficients is also very fast. After about 
50.3 10 samples, the timing coefficients iˆt 
has converged. 
4.2. Hardware Implementation and Validation 
To confirm the effectiveness of the 
proposed technique, the hardware validation on 
the FPGA platform was carried out. The FPGA 
implementation was to validate that the 
proposed calibration method could be 
implemented in hardware. The FPGA design 
and verification flow using hardware co-
simulation with MATLAB/Simulink and Xilinx 
FPGA design tools were utilized in this 
framework so that a VHDL (Very High Speed 
Integrated Circuit Hardware Description 
Language) model of the TIADC was generated 
from the MATLAB/Simulink model. The 
hardware architecture of the proposed 
calibration technique was designed and 
optimized in terms of fixed point representation 
characterized by the signal ranges and signal 
word length optimized by the design tools. 
The hardware based verification flow for 
the proposed technique with the System 
Generator tool in MATLAB simulation and the 
Xilinx FPGA-in-the-loop (FIL) methodology is 
shown in Fig. 9. With the TIADC output 
generated by the computer, both the 
conventional simulation by MATLAB and the 
hardware co-simulation with the FPGA board 
using the FIL methodology were performed. 
The TIADC output signal includes all 
Figure 9. The verification flow for the proposed 
technique with the system generator tool using 
MATLAB simulation and FPGA-in-the-loop (FIL). 
Figure 10. The laboratory measurements for the 
FPGA based implementation. 
deviations as described in Section 2 generated 
by MATLAB 2019a software on the computer. 
These signals are then loaded into the FPGA
V-T. Ta, V-P. Hoang / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 36, No. 2 (2020) 1-11 
8 
Figure 11. Output spectrum of four-channel TIADC with the proposed technique 
on FPGA hardware before and after calibration. 
Figure 12. Output spectrum of four-channel TIADC 
with the proposed technique on FPGA hardware 
before and after calibration for multi-tone sinusoidal 
input signal [0.05 0.18 0.29 0.405]in sf f . 
Table 2. FPGA implementation results 
Device XC7Z020 CLG484-1 SoC 
LUT 9921/53,200 (18.65%) 
LUT RAM 61/17,400 (0.35%) 
Flip-Flop 7035/106,400 (6.61%) 
DSP slices 15/220 (6.82%) 
(a) 
(b) 
Figure 13. The convergence behavior of channel 
mismatches: (a) offset mismatch, (b) timing mismatch.
V-T. Ta, V-P. Hoang / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 36, No. 2 (2020) 1-11 
9 
Table 3. The comparison with the state-of-the-art techniques 
Characteristics [12] 
TCAS-I 2013 
[8] 
TCAS-II 2016 
[11] 
TCAS-I 2018 
This work 
Mismatch types Gain, timing Timing Offset, gain, timing Offset, gain, timing 
Blind Yes Yes Yes Yes 
Background Yes Yes Yes Yes 
Number of sub-ADC 
channels 
Depend on 
Hadamard matrix 
(e.g., 2,4,8...) 
4 Any Depend on 
Hadamard matrix 
(e.g., 2,4,8...) 
Sampling frequency -- 2.7GHz 32GHz 2.7GHz 
Input frequency 0.45fs Multi-tone 0.18fs 0.45fs & Multi-tone 
Number of bits 10 11 9 11 
SNDR improvement (dB) 62 11 36.55 48.1 
SFDR improvement (dB) -- 28 43.72 77.98 
Convergence time (Samples) 60k 10k 400k 30k 
board that has embedded the proposed 
calibration technique through the JTAG USB 
cable. The results after hardware execution 
were fed back into the computer for comparison 
with the simulation results in 
MATLAB/Simulink. The results included 
SNDR, SFDR, the output spectrum, and the 
convergence time. Fig. 10 illustrates the 
settings and experimental results of the 
proposed technique in our laboratory. 
Experimental results on the FPGA hardware 
of the proposed method are shown in Fig. 11, 
Fig. 12 and Fig. 13. The simulation results in 
Fig. 6 and Fig. 7 are quite similar the 
experimental results in Fig. 11 and Fig. 12, 
respectively. The performance of TIADC 
before and after calibration on FPGA hardware 
is also achieved close to simulation. The 
experimental results show that the performance 
of the ADC is improved by 34.03 dB for SNDR 
and 62.07 dB for SFDR. Due to the difference 
between fixed point and floating point 
representations, there was still a slight bias in 
the experimental results. 
The convergence behavior of the estimated 
offset and timing mismatch coefficients on 
FPGA hardware is shown in Fig. 13(a) and Fig. 
13(b), respectively. As can be seen, the 
estimated offset ˆio converges very fast, only 
after 50 samples. The estimated timing 
coefficients iˆt have converged after about 
30000 samples. These results are very identical 
to the simulation ones. 
The implementation results on the FPGA 
hardware (Xilinx ZYNQ-7000 SoC ZC702 
evaluation board) demonstrate that the 
synthesized circuit operates properly and 
consumes very little hardware resources of the 
FPGA chip. These results are shown in Table 2. 
The comparison results of the proposed 
technique with the prior state-of-the-arts is 
shown in Table 3. These results were performed 
through Monte Carlo simulation. These results 
were also compared with the simulation results 
of other techniques. The hardware implementation 
results of the proposed calibration technique on the 
FPGA platform were also higher than other 
techniques. The proposed technique calibrated 
the offset and gain mismatches with simple 
calibration techniques before correct the timing 
mismatch so it reduced the impact on timing 
mismatch calibration. Therefore the 
performance of the proposed technique (SNDR 
and SFDR) is higher than the other techniques. 
In addition, the adaptation step was selected 
appropriately so the convergence time is faster. 
V-T. Ta, V-P. Hoang / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 36, No. 2 (2020) 1-11 
10 
5. Conclusion 
In this paper, a fully digital background 
calibration technique for offset, gain, and 
timing mismatches in M-channel TIADC has 
been presented. The offset mismatch is 
calibrated by taking the average of output 
samples of each channel. The gain mismatch is 
compensated by calculating the power ratio of 
the sub-ADC with the reference ADC. Finally, 
timing skew is compensated by combining the 
LMS adaptive algorithm and the Hadamard 
matrix. The simulation and implementation 
results of a 4-channel TIADC has demonstrated 
a significant improvement in both SNDR and 
SFDR. In future work, we will consider 
bandwidth mismatch to further improve the 
TIADC performance. 
References 
[1] I. Melamed and S. Toledo, A robust, selective, 
and flexible RF front-end for wideband sampling 
receivers, ICT Express 3(2) (2017) 96-100. 
[2] W. C. Black and D. A. Hodges, Time interleaved 
converter arrays, IEEE Journal of Solid-state 
circuits 15(6) (1980) 1022-1029. 
[3] B. Razavi, Design considerations for interleaved 
ADCs, IEEE Journal of Solid-State Circuits 48(8) 
(2013) 1806-1817. 
[4] N. Kurosawa, H. Kobayashi, K. Maruyama, H. 
Sugawara, and K. Kobayashi, Explicit analysis of 
channel mismatch effects in time-interleaved 
ADC systems, IEEE Transactions on Circuits and 
Systems I: Fundamental Theory and Applications 
48(3) (2001) 261-271. 
[5] C. Vogel, The impact of combined channel 
mismatch effects in time-interleaved ADCs, IEEE 
transactions on instrumentation and measurement 
54(1) (2005) 415-427. 
[6] P. J. Harpe, J. A. Hegt, and A. H. van Roermund, 
Analog calibration of channel mismatches in 
time‐ interleaved ADCs, International Journal of 
Circuit Theory and Applications 37(2) (2009) 
301-318. 
[7] D. Camarero, K. B. Kalaia, J.-F. Naviner, and P. 
Loumeau, Mixed-signal clock-skew calibration 
technique for time-interleaved ADCs, IEEE 
Transactions on Circuits and Systems I: Regular 
Papers 55(11) (2008) 3676-3687. DOI: 
10.1109/TCSI.2008.926314. 
[8] H. Le Duc, D. M. Nguyen, C. Jabbour, T. Graba, 
P. Desgreys, and O. Jamin, All-digital calibration 
of timing skews for TIADCs using the polyphase 
decomposition, IEEE Transactions on Circuits and 
Systems II: Express Briefs 63(1) (2015) 99-103. 
[9] H. Le Duc, D. M. Nguyen, C. Jabbour, T. Graba, 
P. Desgreys, and O. Jamin, Hardware 
implementation of all digital calibration for 
undersampling TIADCs, in 2015 IEEE 
International Symposium on Circuits and Systems 
(ISCAS), 2015, pp. 2181-2184. 
[10] L. Guo, S. Tian, and Z. Wang, Estimation and 
correction of gain mismatch and timing error in 
time-interleaved ADCs based on DFT, Metrology 
and Measurement Systems 21(3) (2014) 535-544. 
[11] Y. Qiu, Y.-J. Liu, J. Zhou, G. Zhang, D. Chen, and 
N. Du, All-digital blind background calibration 
technique for any channel time-interleaved ADC, 
IEEE Transactions on Circuits and Systems I: 
Regular Papers 65(8) (2018) 2503-2514. 
[12] J. Matsuno, T. Yamaji, M. Furuta, and T. Itakura, 
All-digital background calibration technique for 
time-interleaved ADC using pseudo aliasing signal, 
IEEE Transactions on Circuits and Systems I: 
Regular Papers 60(5) (2013) 1113-1121. 
[13] S. Saleem and C. Vogel, On blind identification of 
gain and timing mismatches in time-interleaved 
analog-to-digital converters, in 33rd International 
Conference on Telecommunications and Signal 
Processing, Baden (Austria), 2010, pp. 151-155. 
[14] H.-W. Kang, H.-K. Hong, S. Park, K.-J. Kim, K.-
H. Ahn, and S.-T. Ryu, A sign-equality-based 
background timing-mismatch calibration 
algorithm for time-interleaved ADCs, IEEE 
Transactions on Circuits and Systems II: Express 
Briefs 63(6) (2016) 518-522. 
[15] H.-H. Chen, J. Lee, and J.-T. Chen, Digital 
background calibration for timing mismatch in 
time-interleaved ADCs, Electronics Letters 42(2) 
(2006) 74-75. 
[16] S. Liu, N. Lv, H. Ma, and A. Zhu, Adaptive 
semiblind background calibration of timing 
mismatches in a two-channel time-interleaved 
analog-to-digital converter, Analog Integrated 
Circuits and Signal Processing 90(1) (2017) 1-7. 
[17] H. Chen, Y. Pan, Y. Yin, and F. Lin, All-digital 
background calibration technique for timing 
mismatch of time-interleaved ADCs, Integration 
57 (2017) 45-51. 
[18] T. Van-Thanh, H. Van-Phuc, and X. Tran, All-
Digital Background Calibration Technique for 
V-T. Ta, V-P. Hoang / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 36, No. 2 (2020) 1-11 
11 
Offset, Gain and Timing Mismatches in Time-
Interleaved ADCs, EAI Endorsed Transactions on 
Industrial Networks and Intelligent Systems 6(21) 
(2019). DOI: 10.4108/eai.24-10-2019.160983. 
[19] N. Le Dortz et al., 22.5 A 1.62 GS/s time-
interleaved SAR ADC with digital background 
mismatch calibration achieving interleaving spurs 
below 70dBFS, in 2014 IEEE International Solid-
State Circuits Conference Digest of Technical 
Papers (ISSCC), IEEE, 2014, pp. 386-388. 
[20] S. Tertinek and C. Vogel, Reconstruction of 
nonuniformly sampled bandlimited signals using a 
differentiator–multiplier cascade, IEEE Transactions 
on Circuits and Systems I: Regular Papers 55(8) 
(2008) 2273-2286. 
[21] C. Cho et al., Calibration of channel mismatch in 
time-interleaved real-time digital oscilloscopes, in 
2015 85th Microwave Measurement Conference 
(ARFTG), IEEE, 2015, pp. 1-5.