Bài giảng Trường điện từ - Chương 2: Trường điện tĩnh
2.1 Luật Coulomb và nguyên lý xếp chồng.
2.2 Thế điện vô hướng.
2.3 Áp dụng luật Gauss cho trường điện tĩnh.
2.4 Phương trình Poisson Laplace .
2.5 Vật liệu trong trường điện tĩnh.
2.6 Năng lượng trường điện (We ).
2.7 Tụ điện và tính điện dung cuả tụ điện.
2.8 Phương pháp ảnh điện .
2.9 Dòng điện không đổi .

Trang 1

Trang 2

Trang 3

Trang 4
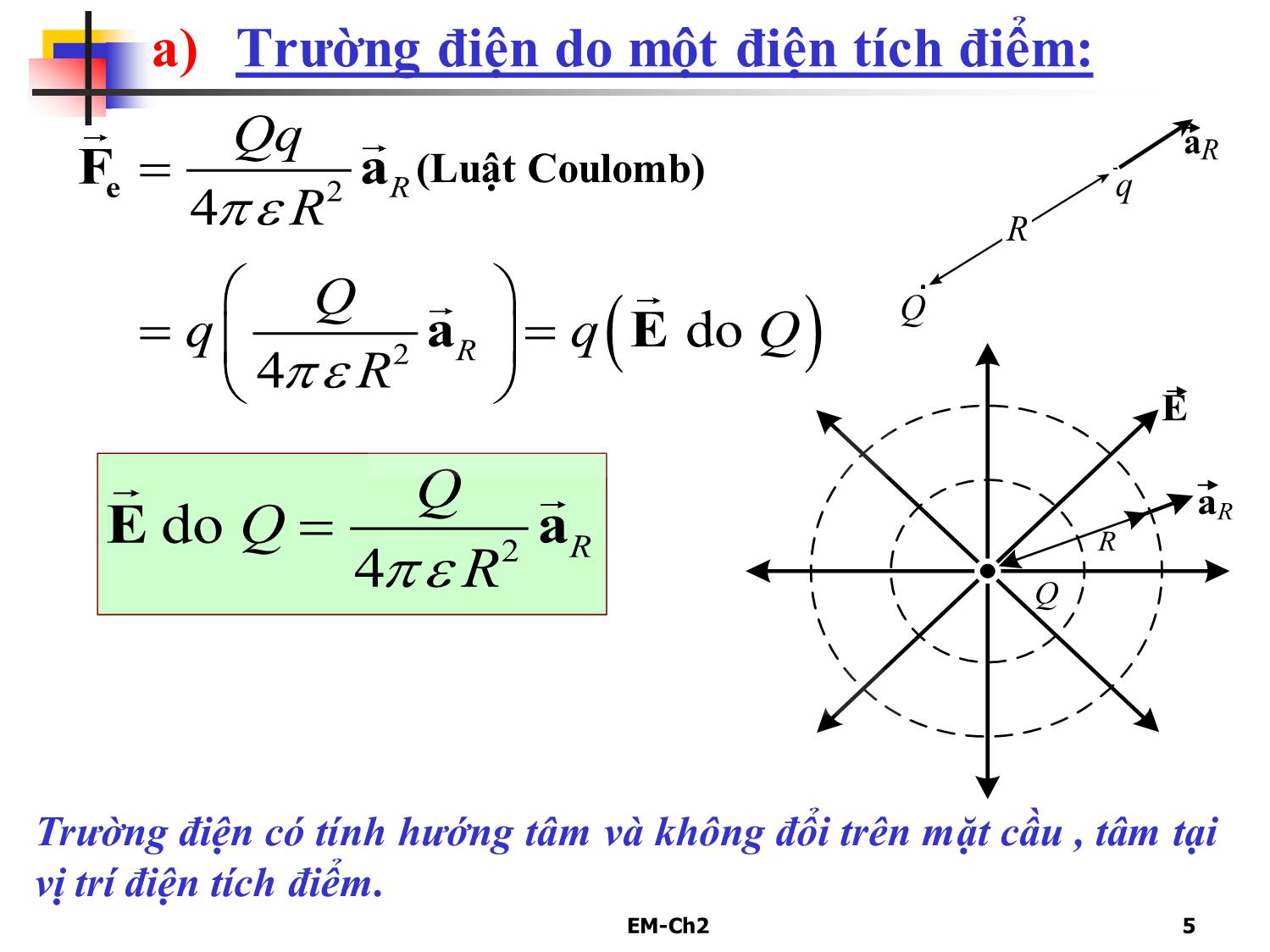
Trang 5
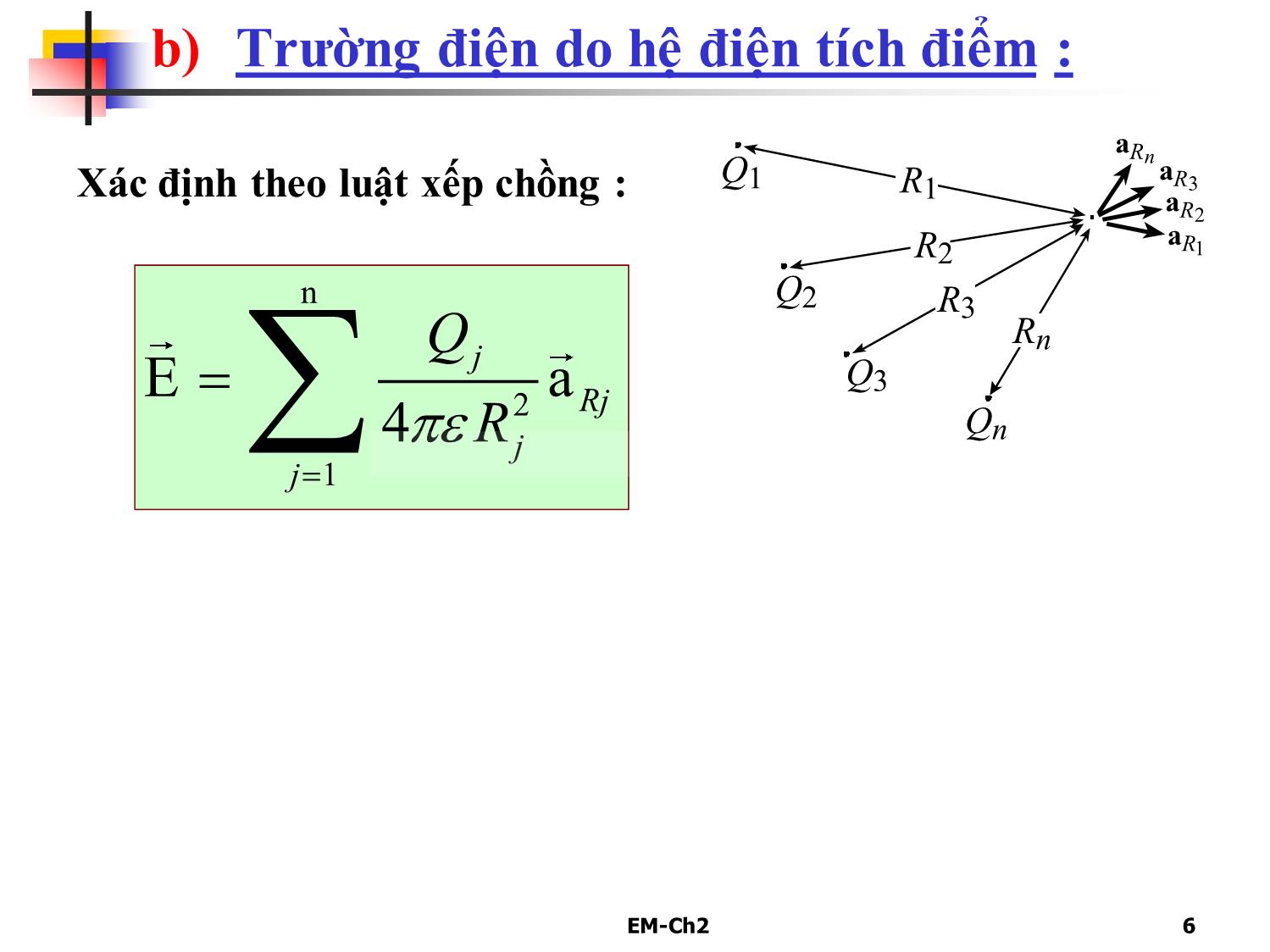
Trang 6
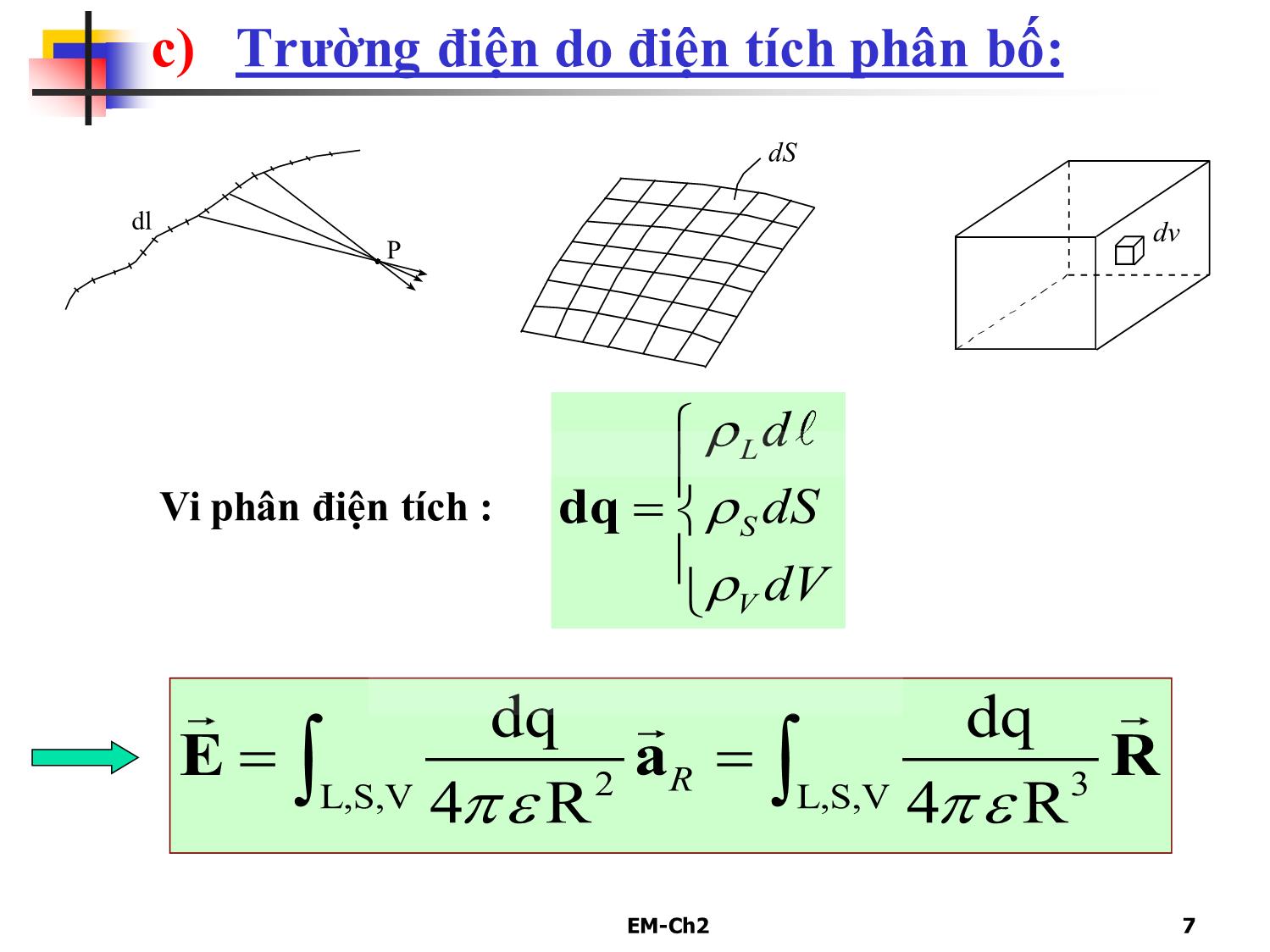
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Trường điện từ - Chương 2: Trường điện tĩnh", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Trường điện từ - Chương 2: Trường điện tĩnh

E a d Đặt tụ dưới hiệu thế U , ta xác định vectơ cường độ trường điện: x U D a d Điện tích cốt tụ tại x = 0 : Luật Gauss tích phân: xQ D .S Điện dung của tụ phẳng: Q C U S C d EM-Ch2 86 VD 2.7.2: Tính điện dung đường dây Tương đương 2 dây dẫn là 2 trục mang điện mật độ dài tại tâm dây dẫn. Đường dây song hành, bán kính dây dẫn là a, hiệu thế U, cách nhau d .Tìm điện dung đơn vị của đường dây ( giả sử d >> a) ? Giải EM-Ch2 87 VD 2.7.2: Tính điện dung đường dây (tt) Thế điện tại 1 điểm bên ngài 2 dây dẫn: ln 2 r r ln ln ln 2 A B d a a d a U a d a a 0Do C U 0C ln d a a EM-Ch2 88 c) Tính C dùng năng lượng trường điện: 2 2 e V V V 1 1 1 D W E.D .E . (J) 2 2 2 dV dV dV Có thể tính We thông qua C hoặc ngược lại. 1 2 Q1 Q2 2 e 1 W CU 2 EM-Ch2 89 VD 2.7.3: Tính C dùng We Đặt tụ đưới hiệu thế điện U ( a = U; b = 0), dùng phương trình Laplace xác định thế điện và cường độ trường điện trong mỗi lớp điện môi: Giải Tính C của tụ cầu gồm 2 lớp điện môi lý tưởng ? 1 2 abU 1 aU (b a) (b a)r 1 2 r2 abU 1 E E a (b a) r EM-Ch2 90 VD 2.7.3: Tính C dùng We (tt) Năng lượng trường điện của hệ: Giải Tính C của tụ cầu gồm 2 lớp điện môi lý tưởng ? 1 2 2 2 e 1 1 2 2 V V 2 2 2 2 1 2 2 2 20 0 0 1 W ε E dV ε E dV 2 ε εa b U sin sin 2(b a) r r b b a a drd d drd d 2 e 1 2 abU W 2 ε ε 2(b a) e 1 22 2W 2 ab C ε ε U (b a) EM-Ch2 91 VD 2.7.4: Tính C tụ không đồng nhất Tụ phẳng, điện môi lý tưởng không đồng nhất hằng số điện môi r = ax + b (a,b =const), nối vào nguồn DC hiệu thế U. a) Giả sử điện tích mặt trên cốt tụ tại x = 0 là S và trên cốt tụ tại x = d là – S. Tính vector cảm ứng điện và cường độ trường điện trong điện môi ? b) Theo câu a), xác định hiệu thế điện U (theo S) và điện dung của tụ ? c) Theo câu a), xác định mật độ điện tích phân cực khối trong điện môi (theo S) ? diện tích A x U r = ax + b + d 0 Mật độ điện tích mặt S – S EM-Ch2 92 VD 2.7.4: Tính C tụ không đồng nhất (tt) Giải diện tích A x U r = ax + b + d 0 Mật độ điện tích mặt S a) Theo xếp chồng: 1 1 S x S x S x2 2 D ρ a ( ρ )( a ) ρ a S 0 ρD 1 xε ε ax b E a b) Theo định nghĩa hiệu thế điện: S S S 0 0 0 d d dρ ρ ρdx ad ε ax b ε a ε a b00 0 U Edx ln(ax b) ln 1 Điện tích trên cốt tụ: Q(x = 0) = A. S. Điện dung của tụ: S 0 S 0 ρ A Aε aQ(x 0) ρ ad adU ln 1 ln 1 ε a b b C EM-Ch2 93 VD 2.7.4: Tính C tụ không đồng nhất (tt) Giải diện tích A x U r = ax + b + d 0 Mật độ điện tích mặt S c) Vector phân cực điện : 0P ( )E S 0 ρ 1 ax b 1 0 x S xε ax b ax b P ε (ax b 1) a ρ a S 2ρ aax b 1PV S x ax b (ax b)ρ divP ρ Điện tích phân cực khối : EM-Ch2 94 VD 2.7.5: Tính C tụ không đồng nhất a) Do tính đối xứng của bài toán, cảm ứng điện có dạng: Tụ trụ, bán kính trong a = 1cm, bán kính ngoài b = 2,5cm, điện môi lý tưởng không đồng nhất hằng số điện môi r = (0,1 + r)/r, nối vào nguồn DC hiệu thế U. Xác định: a) Cường độ trường điện và cảm ứng điện trong điện môi ? b) Điện tích trên cốt tụ trong và điện dung của tụ (bằng số) trên đơn vị dài ? U + a b r rD D a (hệ trụ) Và: divD 0 1 rr r (rD ) 0 A r r D (Với A = const) EM-Ch2 95 VD 2.7.5: Tính C tụ không đồng nhất (tt) U + a b 0 r0,1 b 0,1 a ε U 1 D a rln Vậy: 0 D A 1 rε ε 0,1 r E a Theo định nghĩa hiệu thế điện: 0 0 0 b bA dr A A 0,1 b ε 0,1 r ε ε 0,1 a U ln(0,1 r) ln aa 0,1 b0 0,1 aA ε U / ln r0,1 b 0,1 a U 1 E a 0,1 rln EM-Ch2 96 VD 2.7.5: Tính C tụ không đồng nhất (tt) b) Điện tích trên cốt tụ trong trên 1m: 0 r a 0,1 b 0,1 a ε U 1 Q DdS .2 rlnS r U + a b 1m Điện dung trên đơn vị dài: 12 r a 0 0 0,1 b 0,125 0,1 a 0,11 Q 2 ε 2 .8,842.10 C 434,6 pF U ln ln 0 r a 0,1 b 0,1 a 2 ε U Q ln EM-Ch2 97 2.8 Phương pháp ảnh điện EM-Ch2 98 a) Nguyên tắc: Sự có mặt của điện tích cảm ứng và liên kết: sẽ làm thay đổi phân bố trường điện ban đầu. Việc xác định các loại điện tích này tương đối phức tạp, và dùng luật Gauss để tính trường điện vô cùng khó khăn vì chúng thường phân bố không đều. PP ảnh điện là PP tốt nhất để xác định trường điện mà không cần quan tâm đến việc xác định qui luật các loại điện tích phân bố này. Khi đặt vật mang điện gần các môi trường điện môi hay vật dẫn: theo tính chất của trường điện tĩnh sẽ có sự xuất hiện điện tích cảm ứng và điện tích liên kết. PP ảnh điện ứng dụng rộng rãi trong lý thuyết đường dây và lý thuyết anten. EM-Ch2 99 b) Qui trình phương pháp ảnh điện: b2) Đưa điện tích ảnh (q’) vào môi trường 2 để duy trì điều kiện biên của bài toán. Định lý duy nhất nghiệm: nghiệm không thay đổi trong 2 mô hình vì điều kiện biên và phân bố điện tích không đổi ở môi trường cần tính trường điện. b1) Thay môi trường 2 bằng 1 để đồng nhất hóa môi trường. 1 q (x) P q’ 1 2 q S (x) P Xét bài toán: EM-Ch2 100 c) Các trường hợp cơ bản của phương pháp ảnh điện: EM-Ch2 101 TH1: Phân cách phẳng đmôi – vdẫn: Điện tích q hay trục mang điện trước mặt dẫn rộng vô hạn nối đất. Bài toán: q () d -q (-) d Điện tích -q hay trục mang điện - đối xứng qua bề mặt vật dẫn. Ảnh điện: (trường điện không đổi) q () d EM-Ch2 102 TH2: Phân cách phẳng đmôi - đmôi 1 2 1 21 q q Điện tích q hay trục : 1 2 z d q() 1 1 z d q() d q1(1) (x) P 2 2 z d q2(2) (x) P P ở môi trường 1 P ở môi trường 2 2 1 2 2 2q q EM-Ch2 103 TH3: Phân cách cầu đmôi – vật dẫn Bỏ quả cầu dẫn, và thêm vào điện tích q’ thỏa: Điện tích q đặt trước quả cầu dẫn (bkính a) nối đất. q D a O q a O b q’ 2a b D ' aq D q Nếu quả cầu không nối đất -> thêm điện tích ảnh q1 = -q’ tại tâm O thỏa điều kiện biên thế điệ trên bề mặt quả cầu. EM-Ch2 104 TH4: Phân cách trụ đmôi – vật dẫn 2a b D ' Trục mang điện đặt trước trụ dẫn (bkính a) nối đất. D a O Bỏ trụ dẫn, và thêm vào trục mang điện ’ thỏa: D a O ’ b EM-Ch2 105 VD 2.8.1: Dùng phương pháp ảnh điện Dây dẫn dài vô hạn, mang điện với mật độ dài ℓ = , cách mặt dẫn phẳng nối đất một khoảng là h, tìm mật độ điện tích mặt S tại điểm P(x,h) ? x y 0 h 0 x P conductor Giải Bài toán ảnh điện: x y 0 h 0 x P(x,y) 2h - y r- r+ Thế điện ở miền y < h dùng công thức: 0 λ ln ln 2 r r EM-Ch2 106 VD 2.8.1 : Dùng PP ảnh điện (tt) x y 0 h 0 x P(x,y) 2h - y r- r+ Trường điện ở miền y < h dùng công thức: x yr ( )a ( 2 )ax y h Do: x yr ( )a ( )ax y 2 2 2 2 0 λ ln ( 2 ) ln 2 x y h x y x yE grad a a x y EM-Ch2 107 VD 2.8.1 : Dùng PP ảnh điện (tt) Điện tích mặt tại P : 2 2 2 2 λ 2 2 ( 2 ) y h y h y x y h x y S y 0 0 0 ( ) a [0 ]y h y y h y h E E y x y 0 h 0 x P(x,h) 2h - yn a 2 2( ) S h x y EM-Ch2 108 VD 2.8.2: PP ảnh điện tìm C Điện dung đơn vị của hệ 2 dây dẫn đã xác định ở VD 2.7.2 là : Dây dẫn dài vô hạn, bán kính a, mang điện với mật độ dài ℓ = , cách mặt dẫn phẳng nối đất một khoảng là h (h >> a), tìm điện dung C0 trên đơn vị dài đường dây ? Giải x y 0 h 0 x P conductor 2a Bài toán ảnh điện: x y 0 h 0 2h - 2a 0 0 0C ( λ) 2 2 ln ln h a h a a EM-Ch2 109 VD 2.8.2: PP ảnh điện tìm C (tt) Dây dẫn dài vô hạn, bán kính a, mang điện với mật độ dài ℓ = , cách mặt dẫn phẳng nối đất một khoảng là h (h >> a), tìm điện dung C0 trên đơn vị dài đường dây ? Giải x y 0 h 0 x P conductor 2a Ta suy ra điện dung C0 : 0 0C 2C ( λ) 0 0 2 C 2 ln h a x y 0 h 0 2h - 2a C0 C0 EM-Ch2 110 2.9 Dòng điện không đổi : EM-Ch2 111 a) Trường điện tĩnh ở môi trường dẫn: Môi trường dẫn: ≠ 0. Các đại lượng đặc trưng của trường điện tĩnh trong môi trường dẫn: E, D, and J . 2J σE [A/m ] 0 2J σE [A/m ] 2D E [C/m ] E grad [V/m] Phân loại môi trường: dựa vào độ dẫn điện [S/m]. EM-Ch2 112 Phương trình mô tả & ĐKB: Vρ t divJ ; Từ hệ phương trình Mawell: S ρ 1n 2n t J J divJ 0; Trường điện tĩnh: 1n 2nJ J 0 D εE; J σE Và : Như vậy: v rot E 0 div D ρ divJ 0 1t 2t 1n 2n S 1n 2n E E 0 D D ρ J J 0 EM-Ch2 113 b) ĐKB đối với vector mật độ dòng J : n 1 2a (J J ) 0 1n 2nJ J 0 1n 2n(J J ) 0 (1; 1) n (2; 2) J2 J1 J2n J1n Dùng để xác định thành phần pháp tuyến của trường điện trong môi trường dẫn. EM-Ch2 114 VD 2.9.1: ĐKB đối với vector J z 1 = 2(S/m) 1J 2 = 4(S/m) 2J 2 J Mặt z = 0 là biên 2 môi trường dẫn. Tìm biết 2 1 x z J [5a 10a ] A/m Vector đơn vị ptuyến: zn a Các thành phần của J1 : 1n 1n zJ (J .n)n 10a 1t 1n 1n xJ J J 5a Các thành phần của J2 : 2n 1n zJ J 10a 2 1t 2t 2 2t 2 1t x 1 J J E E 10a 2 2 2n 2t x zJ J J 10a 10a [A/m ] EM-Ch2 115 c) Tính trường điện ở môi trường dẫn: c1) Xác định thế điện trong môi trường dẫn: divJ 0 div[ (grad )] 0 Khi = const : Cách giải 0 Khi ≠ const : div[ (grad )] 0 E J E D E Qui trình: EM-Ch2 116 VD 2.9.2: Trường điện ở mt dẫn E & J Thế điện = (z) là nghiệm ptrình Laplace. U z ĐKB : (ℓ) = U & (0) = 0. A Bz Hệ Đề các, đặt hiệu thế U và ta nhận thấy : = (z). Tụ phẳng, diện tích cốt tụ là A, đặt cách nhau ℓ, điện môi thực có độ dẫn điện = const, nối vào hiệu thế U = const. Tìm phân bố thế điện trong điện môi ? Suy ra vector ? Giải E & J EM-Ch2 117 VD 2.9.3: Trường điện ở mt dẫn U d Ux Nghiệm phương trình Laplace: U xd E a pVdiv D ; div PV Và áp dụng: 0U xd D (5 3x)a U xd J a 0U xd P (4 3x)a Tụ phẳng điện môi thực = (5-3x)0 , = 10-10 S/cm đặt dưới hiệu thế U = 1 KV , khoảng cách giữa 2 cốt tụ là 1 cm. Xác định mật độ dòng trong điện môi, vectơ cảm ứng điện và phân cực điện, suy ra mật độ khối tự do và liên kết ? Giải EM-Ch2 118 c2) Tích phân trực tiếp trường J : Biểu thức của J (và các hằng số tích phân). iii. Áp dụng : suy ra các hằng số tích phân . ab a b U Edl i. Dựa vào phương trình divJ = 0 và tính đốixứng: J E ii. Vectơ c.độ trường điện: (Nếu phụ thuộc tọa độ thì thế ngay ở bước này) J E Edl C D E Qui trình: EM-Ch2 119 Sự tương tự giữa D và J : Môi trường dẫn Môi trường V = 0 rot E 0 ; E grad( ) rot E 0 ; E grad( ) div D 0 div J 0 E, , , J E,... E, , , D εE,... 1t 2t 1n 2nE E 0; D D 0 1t 2t 1n 2nE E 0; J J 0 Chỉ cần thay vị trí của D bằng J trong phương pháp trước. EM-Ch2 120 VD 2.9.4: Sự tương tự giữa D và J Tụ phẳng, diện tích cốt tụ là S, đặt cách nhau d, điện môi thực có độ dẫn điện = const, = const, nối vào hiệu thế U = const. Tìm vector mật độ dòng trong tụ ? Suy ra dòng qua tụ ? Giải Triển khai div trong hệ Cartesian : Jx = A = const. U S I d Dòng điện qua tụ: Do J = Jx.ax và div(J) = 0 . EM-Ch2 121 VD 2.9.5: Sự tương tự giữa và Tụ phẳng, diện tích cốt tụ là A, đặt cách nhau d, điện môi thực có độ dẫn điện = const, = const. Tìm điện trở của tụ điện phẳng ? Giải S C d Kết quả bài toán TĐ tĩnh: ε ; C G Sự tương tự : S G d Điện dẫn của tụ: 1 d R S G Điện trở của tụ: EM-Ch2 122 d) Định luật Joule: Vector mật độ dòng Công suất tiêu tán dạng nhiệt. 2 2 3p J.E σE J /σ [W/m ] Mật độ công suất tiêu tán: 2P p. σE . [W] V VdV dV Công suất tiêu tán trong thể tích V : EM-Ch2 123 e) Điện trở và tính giá trị điện trở : Uab + R G I abU R ( ) I Giá trị điện trở: 1 G conductance[S or ] R Giá trị điện dẫn: EM-Ch2 124 Tính giá trị điện trở : i. Chọn hệ tọa độ. ii. Giả sử Uab = hiệu thế điện đặt lên môi trường dẫn . iii. Xác định vector mật độ dòng trong môi trường dẫn . I J.dS S iv. Xác định dòng qua môi trường dẫn: (dS hướng theo chiều giảm thế) v. Tính: ab U R ( ) I Có thể tính qua công suất: 2 ab 2 U P R ( ) P I EM-Ch2 125 VD 2.9.6: Tính giá trị điện trở của cáp Tìm điện trở trên đơn vị dài của cáp đồng trục, cách điện là điện môi thực có , = const. Giải Đặt lõi và vỏ cáp dưới hiệu thế U. 0 ln(b/a) R 2π Điện trở đơn vị của cáp: r r U 1 E a a ln(b/a)r r Thế điện = (r) là nghiệm ptrình Laplace: Aln Br U [ ln ln b] ln(b/a) r r U 1 J a ln(b/a) r U 1 I .2 ln(b/a) r r (do L = 1m) EM-Ch2 126 VD 2.9.7: Tính điện trở của tụ phẳng x U. J a d x U E a d U d Ux a) Nghiệm ptrình Laplace: Tụ phẳng, điện môi thực, tìm : a) Vectơ trong điện môi thực ? b) Điện trở cách điện của tụ Rcđ ? c) Công suất tổn hao nhiệt trong điện môi? J , E Giaûi EM-Ch2 127 VD 2.9.7: Tính điện trở của tụ phẳng (tt) x S U S J S J .S d db) Có: Irò 2 J V V P J E E dV dVc) Công suất tổn hao nhiệt: Nhận xét: 2 J cd U P R 2 2 J 2 V U U S P d d dV cd ro U d R I S EM-Ch2 128 VD 2.9.8: Tính điện trở thanh dẫn J J a & div J 0 Do tính đối xứng: 1 (J ) 0 r J const J E a Tìm điện trở giữa hai điểm 1-2 , biết ¼ vành khuyên vật dẫn có = 3,3.107 (S/m) ; a = 5 (cm) ; b = 10 (cm) ; bề dày h = 2 (mm) ; dòng điện I = 200 (A). Tìm mật độ dòng (và Jmax) , Rab và công suất tổn hao ? Giaûi EM-Ch2 129 VD 2.9.8: Tính điện trở thanh dẫn (tt) 2 / 2 12 1 0 J J .r U E 2 d l rdCó: 122 UJ .r b h 12 12 S a 0 2 U 2 U h b I J . . ln r a dr dr dz dz I J r.h.ln(b/a) (max) I J a.h.ln(b/a) Mặt khác: 12 12R U / I 2 h ln(b/a) 2 J 12P R I EM-Ch2 130 VD 2.9.9: Tính điện trở cách điện Tụ điện trụ, điện môi thực có độ dẫn điện = k0/r 2 (k0 = const), = const, nối vào nguồn DC có U = const. a) Xác định vector cường độ trường điện trong điện môi ? b) Điện trở cách điện trên đơn vị chiều dài cáp ? Giải r 1 (rJ ) 0 r A r r J r r r 0 J Ar E a a k r rJ J a a) Do tính đối xứng: (hệ trụ) divJ 0 Theo ptrình trường điện tĩnh miền có dòng: EM-Ch2 131 VD 2.9.9: Tính điện trở cách điện (tt) 0 2 2 2k U b a A 0 0 b Ar A 2 2 k 2ka U (b a )dr Theo định nghĩa hiệu thế điện: 2 2 2Ur rb a E a 0 2 2 2k U 1 rrb a J a 0 0 2 2 2 2 2 1 2k U 2k U1 rb a b a0 0 I JdS ( ) 2 m S rd dz b) Dòng rò qua tiết diện cách điện trên đơn vị chiều dài cáp : 2 2 0 U b a I 4πk R
File đính kèm:
 bai_giang_truong_dien_tu_chuong_2_truong_dien_tinh.pdf
bai_giang_truong_dien_tu_chuong_2_truong_dien_tinh.pdf

