Bài giảng Quản lý dự án - Chương 3: Quản lý thời gian của dự án - Đỗ Văn Chính
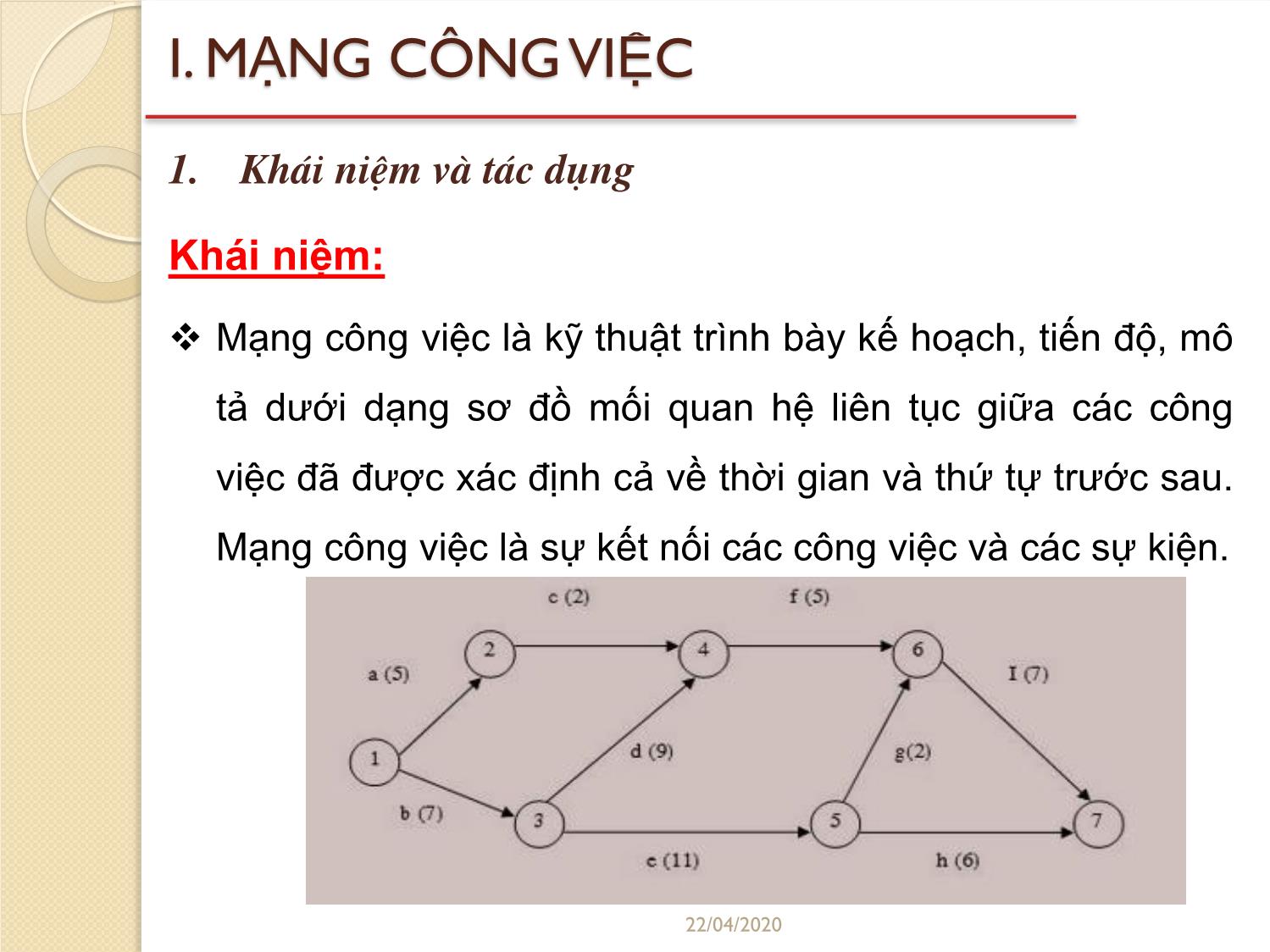
Quản lý thời gian và tiến độ dự án là quá trình quản lý
bao gồm việc thiết lập mạng công việc, xác định thời
gian thực hiện từng công việc cũng nhƣ toàn bộ dự án
và quản lý tiến trình thực hiện các công việc của dự án
trên cơ sở các nguồn lực cho phép và những yêu cầu
về chất lƣợng đã định

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Quản lý dự án - Chương 3: Quản lý thời gian của dự án - Đỗ Văn Chính", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Quản lý dự án - Chương 3: Quản lý thời gian của dự án - Đỗ Văn Chính

22/04/2020
I. MẠNG CÔNG VIỆC
- Phụ thuộc tùy ý
Ví dụ, công việc B có thể xếp sau công việc A khi A đã
hoàn thành nhƣng cũng có thể bố trí cùng thực hiện
song song với công việc A
- Phụ thuộc bên ngoài là mối quan hệ phụ thuộc giữa
các công việc dự án với các cán bộ không thuộc dự
án, là sự phụ thuộc của các công việc dự án với các
yếu tố bên ngoài.
Ví dụ, do trời mƣa nên hôm nay không thể tiếp tục xây
tƣờng nhà (công việc của dự án).
22/04/2020
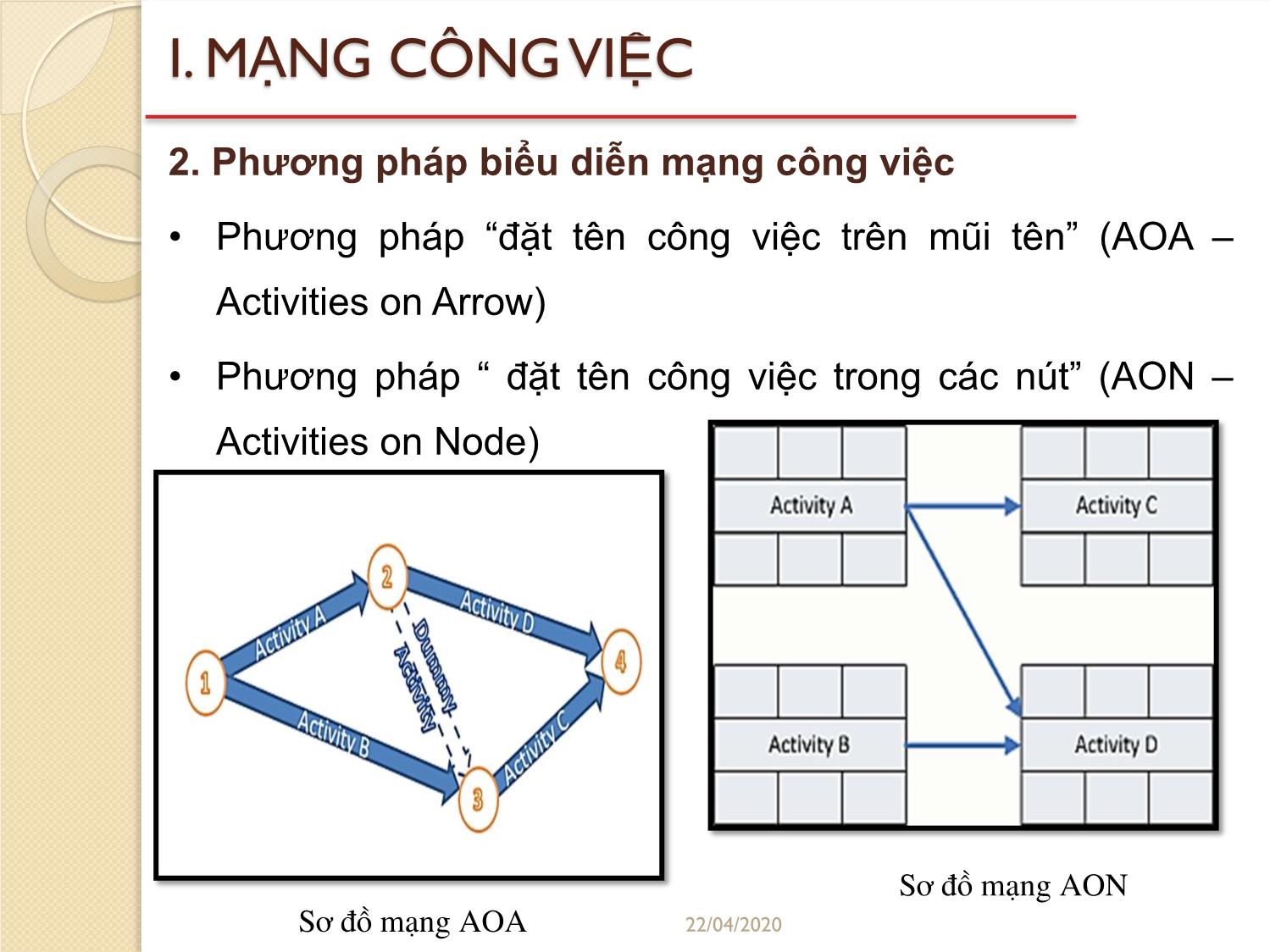
I. MẠNG CÔNG VIỆC
2. Phƣơng pháp biểu diễn mạng công việc
• Phƣơng pháp “đặt tên công việc trên mũi tên” (AOA –
Activities on Arrow)
• Phƣơng pháp “ đặt tên công việc trong các nút” (AON –
Activities on Node)
Sơ đồ mạng AON
Sơ đồ mạng AOA 22/04/2020
I. MẠNG CÔNG VIỆC
Cả 2 phƣơng pháp này đều có chung nguyên tắc là:
để có thể bắt đầu một công việc mới thì các công việc
sắp xếp trước nó phải được hoàn thành, các mũi tên
được vẽ theo chiều từ trái sang phải, phản ánh quan hệ
logic trước sau giữa các công việc nhưng độ dài mũi tên
lại không có ý nghĩa phản ánh độ dài thời gian.
22/04/2020
MẠNG CÔNG VIỆC
Khác nhau:
AOA AON
Mỗi công việc đƣợc đặt trên 1 mũi Mỗi công việc đƣợc đặt vào 1
tên điểm nút (Ô)
Có thể sử dụng biến giả Không có biến giả
Có các sự kiện ở các điểm mút Không có các sự kiện
Các mũi tên không đƣợc giao nhau Các mũi tên có thể giao cắt
và không dùng các đƣờng cong nhau
Cách xây dựng phức tạp và mất Cách xây dựng đơn giản, dễ
nhiều thời gian dàng hơn AOA
22/04/2020
VẼ SƠ ĐỒ MẠNG AOA
Ví dụ: Xây dựng mạng công việc theo phƣơng pháp AOA cho
dự án K bao gồm những công việc nhƣ trong bảng 3.1
Bảng 3.1. Công việc và thời gian thực hiện dự án K
Công Thời gian thực hiện Công việc trước
việc (ngày)
a 2 -
b 4 -
c 7 a
d 5 a
e 3 b,d
22/04/2020
SƠ ĐỒ MẠNG AOA
2
a(2) c(7)
1 d(5) 4
b(4) e(3)
3
Hình 3.1. Xây dựng mạng công việc cho dự án K theo
phương pháp AOA
22/04/2020
VẼ SƠ ĐỒ MẠNG AON
Hoạt động Công việc Thời Hoạt động trƣớc
gian
A Đào đất 3 -
B Đổ nền 4 A
C Dựng ống khói 3 B
D Khung nhà 10 B
E Kết thúc bên ngoài 8 D
F Lắp HVAC 4 D
G Điện sơ bộ 6 D
H Rải đá nền 8 C,E,F,G
I Lắp đặt cabin 5 H
J Sơn 5 H
K Hoàn chỉnh ống khói 4 I
L Hoàn chỉnh điện 2 J
M Lắp nền 4 K,L
22/04/2020
II. SƠ ĐỒ MẠNG LƢỚI PERT/CPM
Các khái niệm:
a. Sự kiện:là mốc đánh dấu sự bắt đầu hay kết thúc của một hoặc một số
CV. Sự kiện kết thúc của 1 hay một số CV cũng đồng thời là sự kiện bắt
đầu của 1 hay một số CV tiếp theo.
Sự kiện ký hiệu bằng khuyên tròn : i
b. Công việc: là 1 quá trình hay tập hợp một số quá trình lao động cần
có chi phí thời gian và hao phí về tài nguyên . Trong thực tế thi công
thời gian chờ đợi vì lý do kỹ thuật hay lý do tổ chức cũng được coi như
khái niệm công việc
Công việc được biểu diễn bằng mũi tên (cung) nối hai sự kiện
với nhau. i j
22/04/2020
II. SƠ ĐỒ MẠNG LƢỚI PERT/CPM
c. Công việc giả (Sự phụ thuộc): là công việc không có thực, không có
hao phí Thời gian và hao phí tài nguyên nhưng nó có tác dụng chỉ
rõ mối quan hệ trước sau giữa các công việc và sự kiện.
i j
d. Đường: là một dãy liên tiếp các CV và CV giả (sự phụ thuộc) nối
các sự kiện với nhau sắp xếp theo thứ tự sao cho sự kiện kết thúc
của CV này trùng với sự kiện bắt đầu của CV tiếp theo làm thành
một đường. Chiều dài của đường bằng tổng độ dài của các CV trên
đường đó và chính là tổng Thời gian của các CV .Trong sơ đồ mạng
có nhiều đường, đường dài nhất trong sơ đồ mạng gọi là đường
găng hay đường trọng điểm.
22/04/2020
II. SƠ ĐỒ MẠNG LƢỚI PERT/CPM
Đường găng là đường nối các sự kiện găng hay các
sự kiện có thời gian dự trữ bằng 0
Đường găng là đường dài nhất trong sơ đồ mạng,
biểu hiện thời gian ngắn nhất mà dự án có thể hoàn
thành
Đường găng là đường dài nhất đi từ sự kiện đầu đến
sự kiện cuối
22/04/2020
II. SƠ ĐỒ MẠNG LƢỚI PERT/CPM
Ký hiệu:
SK1 CV A SK2 CV D SK5
SK3 CV C SK4
22/04/2020
II. SƠ ĐỒ MẠNG LƢỚI PERT/CPM
Các quy tắc và quy ước:
Là một thể thống nhất chỉ bắt đầu bằng 1 sự kiện (SK khởi
công) và cũng chỉ kết thúc bằng 1 sự kiện (SK hoàn thành)
Tất cả các mũi tên biểu diễn công việc và mối liên hệ phải
đều hướng từ trái sang phải hoặc theo chiều thẳng đứng và
phát triển đến sự kiện cuối cùng.
Để thực hiện những công việc song song có tính chất khác
nhau cùng bắt đầu hoặc cùng kết thúc thì phải đưa thêm vào
sơ đồ mạng một số sự kiện phụ và công việc giả
3 k 4 4
5 3 h 5
22/04/2020
II. SƠ ĐỒ MẠNG LƢỚI PERT/CPM
Các quy tắc và quy ước:
Một nhóm công việc tạo thành một mạng con trong sơ đồ
mạng có thể biểu diễn bằng một công việc nếu mạng con đó
chỉ có một sự kiện bắt đầu và một sự kiện kết thúc. Thời gian
của công việc mới bằng thời gian lớn nhất của đường trong
mạng con
5
3
6
4
3 6
22/04/2020
II. SƠ ĐỒ MẠNG LƢỚI PERT/CPM
Các quy tắc và quy ước:
Trong sơ đồ mạng không được có những chu trình khép kín
hoặc các cung giao
4
3 6
5
3 5
4 6
22/04/2020
II. SƠ ĐỒ MẠNG LƢỚI PERT/CPM
Các quy tắc và quy ước:
Công việc giả:
• Nếu công việc d làm sau công việc a, c còn công việc e làm sau
công việc a, b, c thì dùng công việc giả 5 – 6:
a
c d
5
b e
6
• Nếu công việc d làm sau công việc a, c còn công việc e chỉ làm
sau công việc a, b thì dùng công việc giả 5 – 6, 5 – 7
c d
6
a
5
b e
22/04/20207
II. SƠ ĐỒ MẠNG LƢỚI PERT/CPM
Công việc Công việc trƣớc
A -
B -
C A,B
2
A
1 4
C
B
3
22/04/2020
II. SƠ ĐỒ MẠNG LƢỚI PERT/CPM
Công việc Công việc trƣớc
A -
B -
C -
D A
E A,B
F C
2
D
A
B
1 3 5
E
C F
22/04/2020 4
II. SƠ ĐỒ MẠNG LƢỚI PERT/CPM
Công việc Công việc trƣớc
A -
B -
C A,B
D A
E B
2
A D
1 C 5
4
B
E
3
22/04/2020
II. SƠ ĐỒ MẠNG LƢỚI PERT/CPM
Công việc Công việc trƣớc
A -
B -
C -
D A,B,C
E A,B
2
A
E
5
1 3
B
C
D
4
22/04/2020
SƠ ĐỒ MẠNG LƢỚI PERT
Ví dụ 1: Vẽ sơ đồ mạng lưới khi biết các dữ kiện sau:
Công việc Thời gian (ngày) Công việc trƣớc
a 2 -
b 4 -
c 7 a
d 5 a, b
e 3 c,d
22/04/2020
SƠ ĐỒ MẠNG LƢỚI PERT
Ví dụ 2:
Vẽ sơ đồ mạng lưới khi biết các dữ kiện sau:
a
d
a e
b h
KC a,b c,e,f KT
f
i k
c
c g,i
g
22/04/2020
SƠ ĐỒ MẠNG LƢỚI PERT
Ví dụ 3: Vẽ sơ đồ mạng lưới khi biết các dữ kiện sau:
Công việc Công việc trước
a -
b -
c -
d a
e b
f b
g c
h d, e
i d, e
k g, f, h
m i, k
22/04/2020
SƠ ĐỒ MẠNG LƢỚI PERT
Ví dụ 4: Vẽ sơ đồ mạng lưới khi biết các dữ kiện sau:
Công Thời Trình tự
việc hạn thực hiện D,3
2
A 2 Khởi công A,2 G,4 6
B 4 Khởi công I,4
C 4 Khởi công E,6
5
D 3 sau A 1 B,4 3
E 6 sau B
F 12 sau C 7
G 4 sau F, E, D C,4 F,12
I 4 sau G
4 K,3
K 3 sau C
22/04/2020
SƠ ĐỒ MẠNG LƢỚI
Tính toán các thông số sơ đồ mạng lưới
Ký hiệu và quy ước:
i (0) (0) j
t i tij t j
(1) (1) (1) (1)
(0) T t i t j (0) Tj
Ti i Tj
i: Con số đánh dấu sự kiện đầu: là điểm xuất phát công việc
j: Con số đánh dấu sự kiện cuối : là điểm kết thúc công việc
tij: Thời gian cần thiết để thực hiện công việc i,j
(0)
Ti : Thời điểm sớm nhất để hoàn thành sự kiện i
(1)
Ti : Thời điểm muộn nhất hoàn thành sự kiện i
(0)
ti : Thời điểm sớm nhất để khởi công công việc i,j
t (0): Thời điểm sớm nhất để hoàn thành công việc i,j
j 22/04/2020
SƠ ĐỒ MẠNG LƢỚI
Tính toán các thông số sơ đồ mạng lưới
Ký hiệu và quy ước:
i (0) (0) j
t i tij t j
(1) (1)
(0) T (1) t i t j (0) (1)
Ti i Tj Tj
(1)
ti : Thời điểm muộn nhất để khởi công công việc i,j
(1)
tj : Thời điểm muộn nhất để hoàn thành công việc i,j
Dc: Dự trữ chung
Dr: Dự trữ riêng
Dtd: Dự trữ tự do
Dđl: Dự trữ độc lập
22/04/2020
SƠ ĐỒ MẠNG LƢỚI
Nội dung tính toán các tham số:
Thời điểm sớm nhất hoàn thành sự kiện (Ti)
Với mỗi sự kiện i bất kỳ ta cần xác định thời diểm sớm nhất
(0)
hoàn thành sự kiện Ti
(0) (0)
Với sự kiện đầu tiên i = 1: Ti = T1 = 0
Với sự kiện i ≠ 1: thì nó hoàn thành khi mọi công việc ứng
với các cung đi tới đỉnh đó tương ứng đã hoàn thành.
Thời điểm sớm nhất hoàn thành sự kiện i (i = 1,2,3, ... n)
bằng độ dài tính theo thời gian của đường đi dài nhất trên
SĐM từ đỉnh đầu đến đỉnh đó.
22/04/2020
SƠ ĐỒ MẠNG LƢỚI
Nội dung tính toán các tham số:
Thời điểm sớm nhất hoàn thành sự kiện (Ti)
(0) 0 푣ớ푖 푠ự 푖ệ푛 đầ 푖 = 1
푖 = 0
+ 푡 , 푖 푣ớ푖 푖 ≠ 1
Trong đó: k số thứ tự của đỉnh đứng trước kề đỉnh i
t(k,i) thời gian hoàn thành công việc (k,i)
(0)
Thời điểm sớm nhất hoàn thành thời điểm cuối cùng Tn tức
là thời điểm sớm nhất hoàn thành toàn bộ công trình và đường
dài nhất trong SĐM gọi là đường găng.
22/04/2020
SƠ ĐỒ MẠNG LƢỚI
Nội dung tính toán các tham số:
Thời điểm muộn nhất hoàn thành sự kiện (Ti): Mỗi sự kiện
hoàn thành sẽ là điều kiện khởi công các công việc ứng với
các cung đi ra khỏi đỉnh tương ứng và vì vậy thời điểm muộn
nhất hoàn thành mỗi sự kiện là thời điểm giới hạn cho phép
mà theo thời hạn đó công việc (i – j) đang xét có thể kết thúc
nhưng không làm tăng thêm thời gian hoàn thành toàn bộ
công trình.
(1) (0)
Tn = Tn với n là sự kiện cuối cùng của SĐM
(0)
Tn với sự kiện cuối i = n
(1)
Ti =
(1)
Min {Tj - t(i,j) } với i ≠ n
Từ cách tính T(0) ,T(1) của các sự kiện, ta sẽ tìm được
đường găng, là đường mà đi qua các sự kiện có T(0) = T(1)
22/04/2020
SƠ ĐỒ MẠNG LƢỚI
Nội dung tính toán các tham số:
Thời điểm sớm nhất để khởi công và hoàn thành công việc
(0) (0)
(ti , tj )
Mỗi công việc có một sự kiện bắt đầu chỉ sự kiện khởi công và
một sự kiện cuối cùng chỉ sự kiện kết thúc của công việc, vì vậy
ta phải xác định được thời điểm sớm nhất để khởi công và thời
điểm sớm nhất để hoàn thành công việc.
Mỗi công việc có thể bắt đầu khởi công được khi sự kiện đứng
đầu của công việc đã hoàn thành. Như vậy ta có:
- Thời điểm sớm nhất để khởi công công việc :
(0) (0)
ti = Ti
- Thời điểm sớm nhất để hoàn thành công việc :
(0) (0) (0)
tj = ti + tij = Ti +tij
22/04/2020
SƠ ĐỒ MẠNG LƢỚI
Nội dung tính toán các tham số:
Thời điểm muộn nhất để khởi công và hoàn thành công việc:
(1) (1)
(ti , tj )
Sự kiện sẽ hoàn thành khi nào mà công việc ứng với các cung đi
tới đỉnh biểu thị sự kiện đó phải hoàn thành. Như vậy ta có:
Thời điểm muộn nhất để hoàn thành công việc:
(1) (1)
tj = Tj
Thời điểm muộn nhất để khởi công công việc:
(1) (1) (1)
ti = tj - tij = Tj - tij
22/04/2020
SƠ ĐỒ MẠNG LƢỚI
Ví dụ tính toán:
Lập sơ đồ mạng và tính toán các thông số trên sơ đồ mạng cho
một dự án bao gồm 10 công việc, liệt kê theo bảng sau:
Sự Tên công việc Trình tự tiến hành Thời gian
kiện thực hiện
(ngày)
1 1-2 Bắt đầu ngay 4
1-3 Bắt đầu ngay 5
2 2-3 Sau 1-2 3
2-4 Sau 1-2 3
3 3-4 (công việc
ảo)
3-5 Sau 1-3 và 2-3 4
4 4-5 Sau 2-4 6
4-6 Sau 2-4 8
5 5-6 Sau 3-5 và 4-5 7
6 22/04/2020Kết thúc
SƠ ĐỒ MẠNG LƢỚI
Sự kiện Ts2:
Khi công việc 1-2 hoàn thành tức Ts2 = 4 ngày
Sự kiện Ts3: Sự kiện 3 có 2 đƣờng đến 1-2-3 và 1-3
s s s
T 3 = max[(T 2+t23); (T 1+t12)] = max[(4+3); (0+5)] = 7
Sự kiện Ts4: Sự kiện 4 có 2 đƣờng đến 2 - 4 và 3 - 4
s s s
T 4 = max[(T 2+t24); (T 3+t34)] = max[(4+3); (7+0)] = 7
22/04/2020
SƠ ĐỒ MẠNG LƢỚI
Sự kiện Ts5:
Sự kiện 5 có 2 đƣờng để đến 3-5 và 4-5
s s s
T 5 = max[(T 3+t35); (T 4+t45)] = max[(7+4); (7+6)] = 13
Sự kiện 6 Ts6:
Sự kiện 6 có 2 đƣờng để đến 4-6 và 5-6
s s s
T 6 = max[(T 4+t46); (T 5+t56)] = max[(7+8); (13+7)] = 20
22/04/2020
SƠ ĐỒ MẠNG LƢỚI
Thời gian muộn Tm
Từ sự kiện cuối Tm6
Tm6 = Ts6 = 20
Từ 6 lùi về 5 chỉ có một đƣờng, vì vậy
m m
T 5 = T 6 – t56 = 20 – 7 = 13
Xét sự kiện 4: Về 4 có 2 đƣờng là 6-4 và 5-4
Theo đƣờng 6-4: Tm4 = Tm6 – 8 = 20–8 = 12
Theo đƣờng 5-4: Tm4 = Tm5 – 13 = 13-6 = 7
Ta chọn giá trị min của 2 giá trị là Tm4 = 7
SƠ ĐỒ MẠNG LƢỚI
Thời gian muộn Tm
Xét sự kiện 3.
Về 3 có hai đƣờng là 5-3 và 4-3
m m m
T 3 = Min (T 5 – t53; T 4 – t43) = 7
Xét sự kiện 2. Về 2 có hai con đƣờng là 4-2 và 3-2
Theo đƣờng 4-2: Tm2 = Tm4 – 3 = 7–3 = 4
Theo đƣờng 3-2: Tm2 = Tm3 – 3 = 7–3 = 4
Ta chọn giá trị min của 2 giá trị là Tm2 = 4
Và sau cùng ở sự kiện bắt đầu Tm1 = 0
SƠ ĐỒ MẠNG LƢỚI
Thời gian dự trữ của các sự kiện Di
Thời gian dự trữ của sự kiện i, Di là thời gian sự kiện có thể
chậm lại mà không làm ảnh hƣởng thời gian hoàn thành dự
án
Nếu thời gian dự trữ SK bằng 0 ta gọi là các sự kiện găng.
Công việc găng khi công việc có sự kiện đầu và cuối điều
găng
Đƣờng Găng (Critical path)
Đƣơng găng là đƣờng qua các sự kiện găng và là đƣờng có
thời gian là dài nhất.
22/04/2020
SƠ ĐỒ MẠNG LƢỚI
Thời gian dự trữ của công việc
. Thời gian dự trữ toàn phần của một công việc (Dij) nào đó là
khoảng thời gian công việc này có thể kéo dài thêm nhƣng không
làm chậm ngày kết thúc dự án
Dij = Thời gian bắt đầu muộn công việc ij – thời gian bắt đầu
(1) (0) (1) (0)
sớm của công việc ij = ti - ti = tj - tj
. Thời gian dự trữ tự do (dij) là thời gian mà một công việc nào đó
có thể kéo dài thêm nhƣng không làm chậm ngày bắt đầu của
công việc tiếp sau
dij (a) = Min (thời gian bắt đầu sớm của tất cả cv sau a) – thời
ế ớ ủ ệ
gian k t thúc s m c a công vi 22/04/2020c a
BIỂU ĐỒ GANTT
Biểu đồ GANTT là phương pháp trình bày tiến trình thực tế
cũng như kế hoạch thực hiện các công việc của dự án theo
trình tự thời gian.
Mục đích của GANTT là xác định một tiến độ hợp lý nhất để
thực hiện các công việc khác nhau của dự án. Tiến độ này tùy
thuộc vào độ dài công việc, những điều kiện ràng buộc và kỳ
hạn phải tuân thủ.
22/04/2020
BIỂU ĐỒ GANTT
Cấu trúc: Cột dọc trình bày công việc. Thời gian thực hiện từng công
việc được trình bày trên trục hoành. Mỗi đoạn thẳng biểu hiện một
công việc. Độ dài đoạn thẳng là độ dài công việc. Vị trí đoạn thẳng
thể hiện quan hệ thứ tự trước sau giữa các công việc
22/04/2020
BIỂU ĐỒ GANTT
Ưu điểm:
Dễ đọc, dễ nhận biết hiện trạng thực tế của từng nhiệm vụ
cũng như tình hình chung của toàn bộ dự án.
Thông qua biểu đồ có thể thấy được tình hình nhanh chậm
của các công việc, và tính liên tục của chúng.
Biểu đồ thường có một số ký hiệu riêng để nhấn mạnh những
vấn đề liên quan đặc biệt đến công việc.
Hạn chế:
Không thể hiện được mối quan hệ giữa các công tác, không
ghi rõ quy trình công nghệ.
Chỉ phù hợp áp dụng cho những dự án có quy mô nhỏ, không
phức tạp.
22/04/2020 File đính kèm:
 bai_giang_quan_ly_du_an_chuong_3_quan_ly_thoi_gian_cua_du_an.pdf
bai_giang_quan_ly_du_an_chuong_3_quan_ly_thoi_gian_cua_du_an.pdf

