Bài giảng Ôtômát và ngôn ngữ hình thức - Chương 3: Văn phạm chính quy và ôtômát hữu hạn - Nguyễn Thị Thùy Linh

q 1 q F 
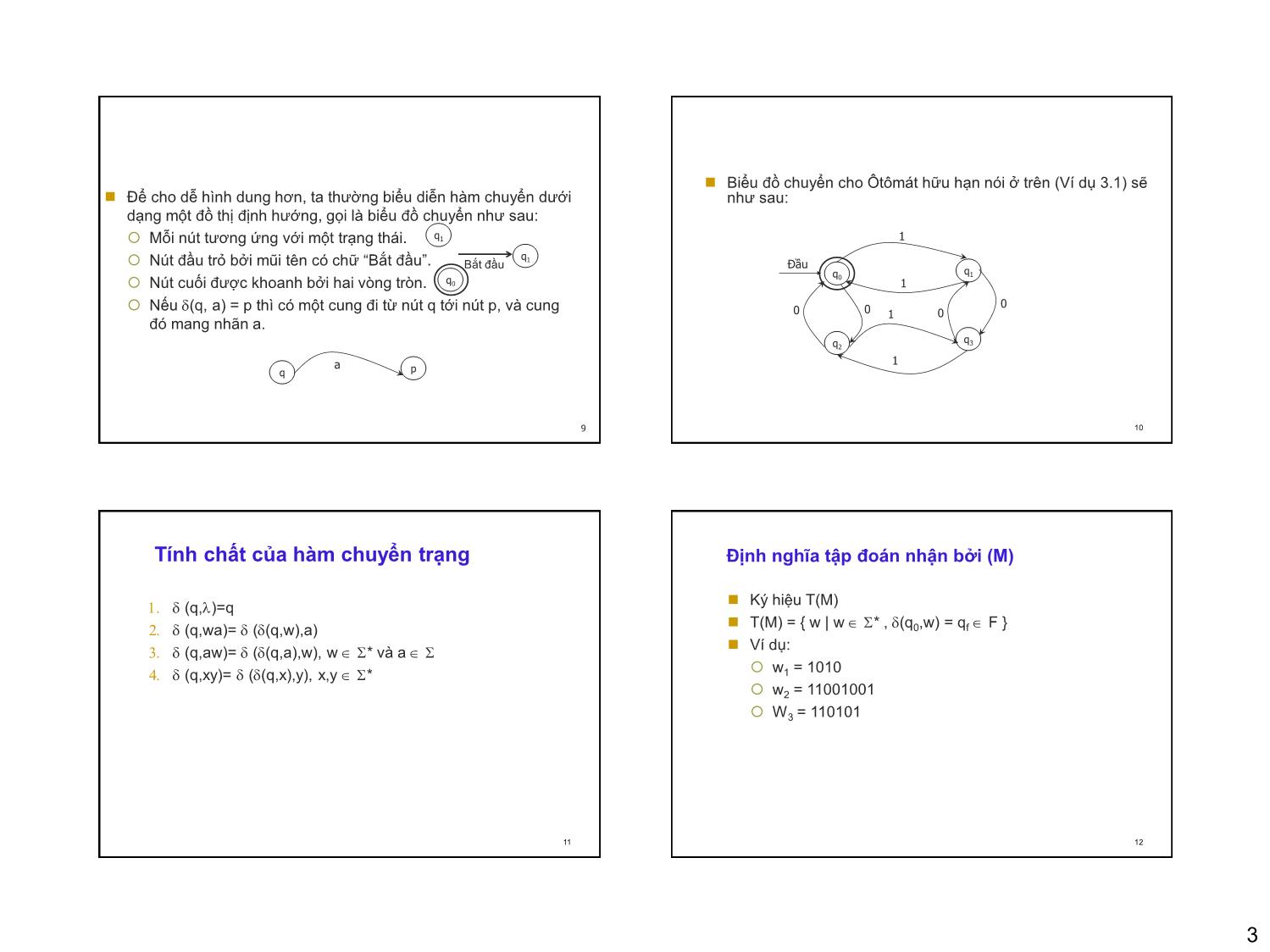
 0 0 0 3 4 4  L (M) = { w00w, w11w | w * ={0,1}*} 
 Đây chỉ là một quá trình đoán nhận trong nhiều quá trình. 
 19 20 
 5 
 Sự tương đương giữa ÔHĐ và ÔHK Sự tương đương giữa ÔHĐ và ÔHK (tt) 
 Theo định nghĩa mỗi ÔHĐ cũng là một ÔHK, cho nên: • Mỗi phần tử trong Q’ được ký hiệu bởi tập hợp {q1, q2, 
 , q }, với q , q , , q Q. 
 L(ÔHĐ)  L(ÔHK) (1) k 1 2 0
 • Trạng thái đầu q0’ = {q0}. 
 Định lý 3.1: Nếu L một ngôn ngữ được đoán nhận bởi một 
  B2 : Hàm chuyển ’ của M’ được thành lập theo công thức: 
 ÔHK, thì cũng có một ÔHĐ đoán nhận L. 
 Nói cách khác L(ÔHK)  L(ÔHĐ) (2) 
 (q , a) 
 ’({q1, q2, , qk}, a) = i 
 Giải thuật: Input: M = (, Q, , q0, F) là ÔHK đoán nhận L. 
 Output: M’ = ( , Q’, ’, q ’, F’) là OHĐ sao cho L(M’)=L(M) 
   0  B3: Vẽ đồ thị chuyển trạng thái 
 B1: Đặt M’ = (, Q’, ’, q ’, F’), trong đó: 
 0  B4: Kết luận M’ và chú thích rõ 5 phần của Ôtômát 
 • Q’ = 2Q 
  Với cách thành lập M’ trên ta hoàn toàn CM được L(M) = L(M’) (Tham khảo 
 • F’ là tập mọi trạng thái trong Q’ có chứa một trạng thái cuối 
 sách “Ngôn ngữ hình thức” – Nguyễn Văn Ba, trang 32). 
 nào đó của M. 
 21 22 
 Sự tương đương giữa ÔHĐ và ÔHK (tt) 
  Ví dụ 3.3: Cho M = ({0, 1}, {q0, q1, q2}, , 
 q0, {q2}), là một ÔHK trong đó hàm chuyển • Kết luận : 
 trạng thái như sau: 
 M’ =( , Q’, ’, {q0}, F’) là OHĐ cần tìm. 
 (q0, 0) = {q0, q1} 
 (q0, 1) = {q1} Trong đó: 
 
 (q1, 0) = {q2} = 
 Q’ = 
 (q1, 1) =  
 ’ (vẽ đồ thị Chú ý: cắt bỏ các nhánh không xuất phát từ q hoặc 
 (q2, 0) = {q2} 0
 xuất phát từ q0 nhưng không kết thúc được) 
 (q2, 1) = {q2} 
 q là trạng thái bắt đầu 
 Tìm OHĐ tương đương? 0 
 F’ = 
 23 24 
 6 
 Sự tương đương giữa ÔHĐ và ÔHK (tt) 
  Thực ra trong 2Q thường có nhiều phần tử Bổ đề 3.1: 
  Lớp các ngôn ngữ đoán nhận bởi Ôtômát hữu 
 không thể truy đạt từ {q0}, nên chẳng cần đưa 
 chúng vào Q’. Vậy để lập Q’, ta nên truy xuất hạn đơn định (hay không đơn định) là một, và 
 gọi là lớp các ngôn ngữ chính quy (viết tắt là 
 từ {q0}, rồi từng bước thêm dần các trạng thái 
 mới, nếu các trạng thái này là kết quả của hàm NNCQ). 
 chuyển thái áp dụng lên các trạng thái đã có  NNCQ được sinh ra bởi VPCQ nên VPCQ có 
 trước đó. mối quan hệ mật thiết với OH. Nghĩa là 
 L(G)=L(M)=L là NNCQ 
 25 26 
 Cho ôtômát hữu hạn đơn định xây dựng VPCQ 
 Văn phạm chính quy 
  Định lý 3.2: Nếu L là một NNCQ trên bộ chữ cái , thì tồn tại một VPCQ phải G sao cho L – 
 {} = L(G). 
 Định nghĩa VPCQ (nhắc lại): Giải thuật: (xây xựng một VPCQ phải từ một ôtômát hữu hạn đơn định) 
 • Một văn phạm chính quy phải nếu tập luật sinh của nó dạng: Input: L = L(M) với M = (, Q, , q0, F) là ÔHĐ. 
 A wB | w, với w * và A, B . Output:Ta thành lập văn phạm G = (T, V, P, S) sao cho L(G)=L \ {} 
 • Một văn phạm chính quy trái nếu tập luật sinh của nó dạng: Input Output 
 M = (, Q, , q0, F) G = (T, V, P, S) 
 A Bw |w, với w * và A, B . 
  T =  
 • Các văn phạm chính quy phải và trái được gọi chung là văn 
 Q = {q q q } V = {V ,V ,V ,} 
 phạm chính quy (viết tắt là VPCQ). 0, 1, 2,. 0 1 2
  P= 
 • Ngôn ngữ được sinh ra bởi VPCQ gọi là NNCQ. 
 (q0, a) = q1 V0 aV1 
 (q1, a) = qf F V1 aVf | a 
 a  và q0,q1 Q a T 
 q0 S là kí hiệu bắt đầu trong P 
 F  Q 
 27 28 
 7 
 GIẢI 
 a b c 
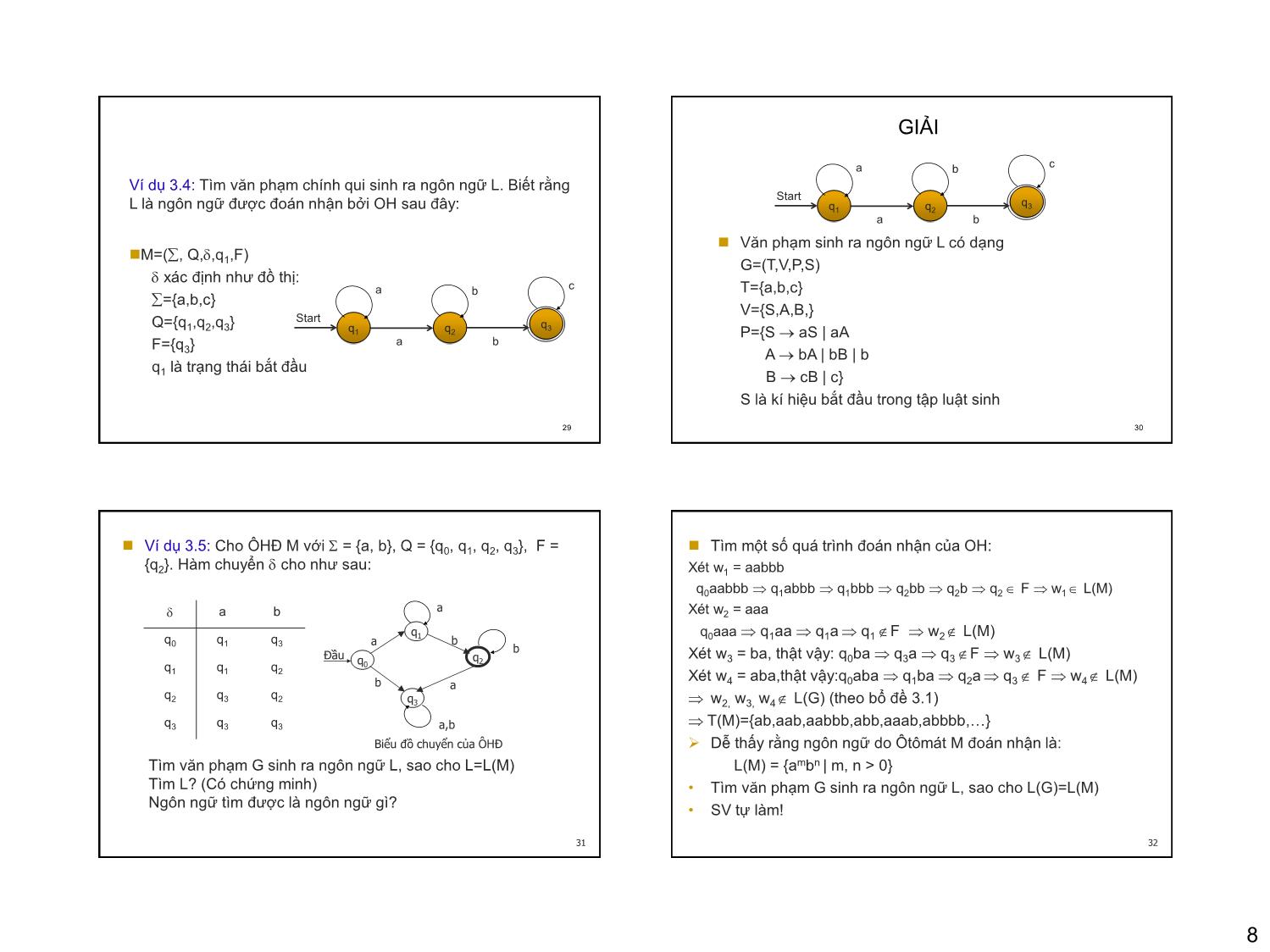
 Ví dụ 3.4: Tìm văn phạm chính qui sinh ra ngôn ngữ L. Biết rằng 
 Start 
 q
 L là ngôn ngữ được đoán nhận bởi OH sau đây: q1 q2 3 
 a b 
  Văn phạm sinh ra ngôn ngữ L có dạng 
 M=(, Q,,q ,F) 
 1 G=(T,V,P,S) 
  xác định như đồ thị: 
 a b c T={a,b,c} 
 ={a,b,c} 
 V={S,A,B,} 
 Start 
 Q={q1,q2,q3} q3 
 q1 q2 P={S aS | aA 
 F={q } a b 
 3 A bA | bB | b 
 q là trạng thái bắt đầu 
 1 B cB | c} 
 S là kí hiệu bắt đầu trong tập luật sinh 
 29 30 
 Ví dụ 3.5: Cho ÔHĐ M với  = {a, b}, Q = {q0, q1, q2, q3}, F =  Tìm một số quá trình đoán nhận của OH: 
 {q2}. Hàm chuyển  cho như sau: Xét w1 = aabbb 
 q0aabbb q1abbb q1bbb q2bb q2b q2 F w1 L(M) 
 a 
  a b Xét w2 = aaa 
 q q aaa q aa q a q F w L(M) 
 q q q a 1 b 0 1 1 1 2 
 0 1 3 b 
 Đầu Xét w = ba, thật vậy: q ba q a q F w L(M) 
 q q2 3 0 3 3 3 
 q q q 0 
 1 1 2 Xét w = aba,thật vậy:q aba q ba q a q F w L(M) 
 b a 4 0 1 2 3 4 
 q q q
 2 3 2 q3 w2, w3, w4 L(G) (theo bổ đề 3.1) 
 q3 q3 q3 a,b T(M)={ab,aab,aabbb,abb,aaab,abbbb,} 
 Biểu đồ chuyển của ÔHĐ  Dễ thấy rằng ngôn ngữ do Ôtômát M đoán nhận là: 
 Tìm văn phạm G sinh ra ngôn ngữ L, sao cho L=L(M) L(M) = {ambn | m, n > 0} 
 Tìm L? (Có chứng minh) • Tìm văn phạm G sinh ra ngôn ngữ L, sao cho L(G)=L(M) 
 Ngôn ngữ tìm được là ngôn ngữ gì? • SV tự làm! 
 31 32 
 8 
 Cho VPCQ xây dựng ôtômát hữu hạn không đơn định Cho VPCQ xây dựng ôtômát hữu hạn không đơn định 
  Cách xây dựng hàm chuyển trạng thái  
 Input Output 
 Định lý 3.3: Nếu G là một VPCQ 
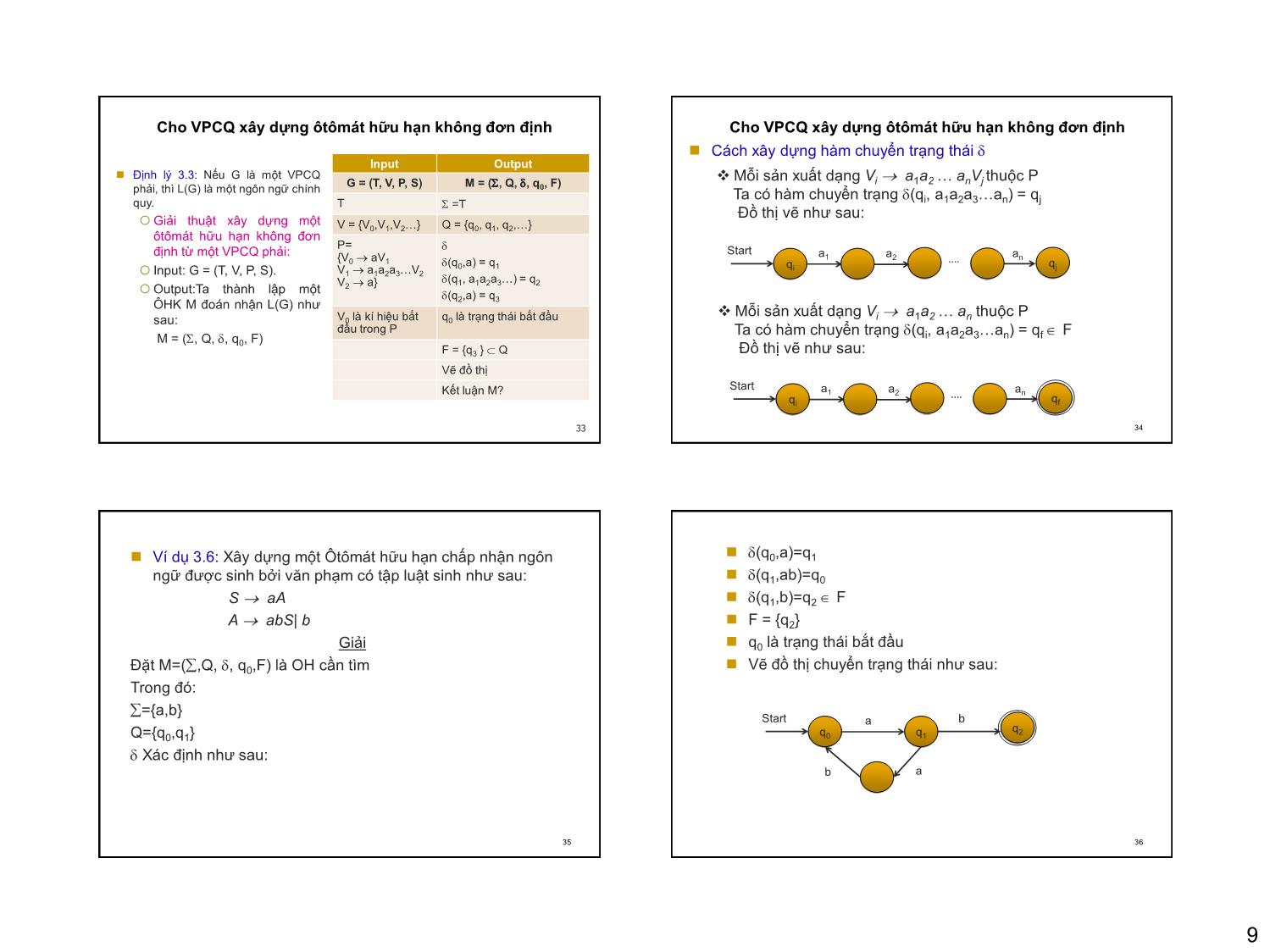
 G = (T, V, P, S) M = (, Q, , q , F)  Mỗi sản xuất dạng Vi a1a2  anVj thuộc P 
 phải, thì L(G) là một ngôn ngữ chính 0 Ta có hàm chuyển trạng (q , a a a a ) = q
 quy. T  =T i 1 2 3 n j 
 Đồ thị vẽ như sau: 
 Giải thuật xây dựng một 
 V = {V0,V1,V2} Q = {q0, q1, q2,} 
 ôtômát hữu hạn không đơn 
 P=  Start 
 định từ một VPCQ phải: a1 a2 an 
 {V0 aV1 (q ,a) = q . q
 Input: G = (T, V, P, S). V a a a V 0 1 qi j 
 1 1 2 3 2 (q , a a a ) = q
 V2 a} 1 1 2 3 2 
 Output:Ta thành lập một (q ,a) = q
 ÔHK M đoán nhận L(G) như 2 3 
  Mỗi sản xuất dạng Vi a1a2  an thuộc P 
 sau: V0 là kí hiệu bắt q0 là trạng thái bắt đầu 
 đầu trong P 
 Ta có hàm chuyển trạng (qi, a1a2a3an) = qf F 
 M = (, Q, , q0, F) 
 F = {q3 }  Q Đồ thị vẽ như sau: 
 Vẽ đồ thị 
 Start a a a
 Kết luận M? 1 2 . n 
 qi qf 
 33 34 
  Ví dụ 3.6: Xây dựng một Ôtômát hữu hạn chấp nhận ngôn  (q0,a)=q1 
 ngữ được sinh bởi văn phạm có tập luật sinh như sau:  (q1,ab)=q0 
 S aA  (q1,b)=q2 F 
 A abS| b  F = {q2} 
 Giải  q0 là trạng thái bắt đầu 
 Đặt M=(,Q, , q0,F) là OH cần tìm  Vẽ đồ thị chuyển trạng thái như sau: 
 Trong đó: 
 ={a,b} 
 Start a b 
 q2 
 Q={q0,q1} q0 q1 
  Xác định như sau: 
 b a 
 35 36 
 9 
 Kết luận M=(,Q, , q0,F) là OH cần tìm ÔHĐ không xuất phát lại 
 • Trong đó: 
 • ={a,b} •Định nghĩa: Một ÔHĐ là không xuất phát lại nếu 
 không tồn tại cặp (q, a) để cho (q, a) = q0 với q0 là 
 • Q={q0,q1,q2,q3} trạng thái đầu 
 •  Xác định như sau: 
 •Bổ đề 3.2: Có giải thuật cho phép biến đổi một ÔHĐ 
 • F = {q } 
 2 M đã cho thành một ÔHĐ không xuất phát lại M’ sao 
 • q0 là trạng thái bắt đầu cho L(M’) = L(M). 
 Giải thuật: 
 Start a b 
 q
 q0 q1 2 
 –Giả sử M = (, {q0, q1, , qn}, , q0, F). 
 b a –Lập ÔHĐ M’ = (, Q  {qn+1}, ’, q0, F’) trong đó: 
 q3 
 37 38 
 ÔHĐ không xuất phát lại  Ví dụ 3.7: Tìm OHĐ không xuất phát lại M’ tương đương với 
 OHĐ có xuất phát lại M sao cho L(M’)=L(M) 
 (q,a) Nếu q Q và (q, a) q0 
 '(q,a) 
 q
 n 1 Nếu q Q và (q, a) = q 
 0 (M) 
 ’(qn+1, a) = ’(q0, a) 
 Gợi ý 
 F Nếu q0 không thuộc F 
 F' OHĐ không xuất phát lại cần tìm sẽ có đồ thị chuyển trạng 
 Nếu q F 
 F {qn 1} 0 thái sau: 
Kết luận M' (, Q  {qn+1}, ’, q0, F’) , chú thích 5 phần? 
Dễ thấy M’ thực hiện cùng các bước chuyển như M, trừ khi 
 (M’) 
M chuyển về q0 thì M’ chuyển sang qn+1, nhưng sau đó lại tiếp 
tục bắt chước như M thường. 
 39 40 
 10 
 Các tính chất đóng của lớp các NNCQ (tt) 
 Gọi M’=(, Q  {qn+1}, ’, q0, F’) là OHĐ cần tìm 
 Trong đó:  Định lý 3.4: Nếu L và L’ là các NNCQ thì L  L’ cũng là NNCQ. 
 ’ a b 
  = {a,b}  Định lý 3.5: Nếu L  * là một NNCQ, thì * - L cũng là NNCQ. 
 q0 q3 q1 
 Q = {q0, q1,q2,q3 }  Định lý 3.6: Nếu L và L’ là các NNCQ thì L  L’ cũng là NNCQ. 
 q q  
 F’ = {q ,q ,q } 1 2 Bổ đề 3.3: Cho L  * và   ’. Có một ÔH với bộ chữ vào  
 0 2 3 q q
 2  3 đoán nhận L khi và chỉ khi có một ÔH với bộ chữ vào ’ 
 q0 là trạng thái bắt đầu 
 q3 q3 q1 đoán nhận L. (Nói cách khác khái niệm NNCQ không tùy 
 ’ như đồ thị 
 thuộc vào bộ chữ). 
  Định lý 3.7: Nếu L và L’ đều là các NNCQ thì LL’ cũng là 
 NNCQ. 
  Định lý 3.8: Nếu L là NNCQ thì L* cũng là NNCQ. 
 41 42 
 BIỂU THỨC CHÍNH QUI 
 Định lý KLEENE 
  Cách khác để mô tả ngôn ngữ chính qui là dùng biểu 
 thức chính qui (BTCQ). 
  Định lý:  và {} là các NNCQ.  Một BTCQ là sự kết hợp: 
  Định lý: Với mọi w *, thì {w} là NNCQ. Các ký tự trong , mỗi ký tự có thể xuất hiện nhiều 
  Hệ quả: Mọi tập con hữu hạn của * đều là NNCQ. lần, 
  Hệ quả: Mọi ngôn ngữ tạo nên từ các ngôn ngữ hữu Các toán tử: bao đóng (+,*), ghép, hợp 
 hạn bằng cách áp dụng một số hữu hạn lần các phép Các dấu ngoặc: () 
 hợp, ghép tiếp và * đều là NNCQ.  VD: 
  Định lý KLEENE: Mọi NNCQ đều có thể nhận được từ  Với ngôn ngữ L= {a}, ta có BTCQ là a 
 các ngôn ngữ hữu hạn bằng cách áp dụng một số hữu  L={a,b}, ta có BTCQ là a+b 
 hạn lần các phép hợp, ghép tiếp và *. 
  L={ab}  {a}, ta có BTCQ là ab+a 
  L={a,b} . {a} , ta có BTCQ là (a+b)a 
 43 44 
 11 
 Biểu thức chính qui 
 Biểu thức chính qui (tt) 
 Định nghĩa 1: Cho  là một bộ chữ. Một biểu thức chính quy 
 (viết tắt là BTCQ) trên  và tập hợp do nó định nghĩa được chỉ  Các toán tử ưu tiên trong BTCQ từ cao tới thấp: 
 định được định nghĩa một cách đệ quy như sau: (1) Bao đóng : 
 1. Các biểu thức chính qui nguyên tố gồm: 0+ : số 0 được lặp lại ít nhất 1 lần, nhiều nhất n lần. 
  là một biểu thức chính quy biểu thị tập rỗng. 
 0* : số 0 được lặp lại ít nhất 0 lần, nhiều nhất n lần 
  là một biểu thức chính quy biểu thị tập {}. 
  a  thì a là một biểu thức chính quy biểu thị tập {a}. (2) Ghép : . 
 2. Nếu r và s là các biểu thức chính quy, lần lượt chỉ định các (3) Hợp : + 
 tập R và S, thì (r+s), (rs), và (r*) là các biểu thức chính quy, và Khi viết một BTCQ, ta có thể bỏ qua một số ngoặc 
 lần lượt biểu thị các tập R  S, RS, và R*. đơn, chẳng hạn, ((0(1*))+0) có thể viết thành 01* + 0 
 3. Một BTCQ nếu và chỉ nếu nó có thể được xây dựng từ các vẫn dễ hiểu. 
 biểu thức chính qui nguyên tố bởi áp dụng một số hữu hạn lần * +
 các qui tắc trong mục 2.  Ta cũng có thể viết tắt biểu thức rr bởi r . 
 45 46 
 Biểu thức chính qui (tt) Biểu thức chính qui (tt) 
  Liên kết giữa ngôn ngữ với BTCQ 
  00 là một biểu thức chính quy chỉ định tập L={00} 
 Tập hợp các chuỗi được chỉ định bởi một BTCQ r được ký hiệu bởi L(r). Để cho 
 *
  (0+1) chỉ định tập mọi chuỗi 0 và 1 tiện ta dùng r vừa để chỉ biểu thức chính quy, vừa để chỉ tập hợp do nó chỉ 
  (1+10)* chỉ định tập mọi chuỗi 0 và 1, có con 1 ở đầu và không định. 
 có hai con 0 liên tiếp.  Định nghĩa 2: 
  (0+)(1+10)* chỉ định tập mọi chuỗi 0 và 1 không chứa hai con 0 Ngôn ngữ L(r) được biểu thị bởi bất kỳ một BTCQ r nào, thì được định nghĩa 
 bởi các qui tắc sau: 
 liên tiếp. Cách khác (1+01)*(0+ ) 
 1.  là một biểu thức chính qui biểu thị tập rỗng. 
 *
  (0+1) 011 chỉ định tập mọi chuỗi 0, 1 kết thúc bởi 011. 2.  là một biểu thức chính qui biểu thị tập {}. 
  0*1*2* chỉ định tập mọi chuỗi gồm một số con 0, tiếp đến một số 3.  a  thì r = a là một biểu thức chính qui biểu thị tập 
 con 1, rồi đến một số con 2. L(r) = {a}. 
  00*11*22* chỉ định tập các chuỗi trong đó 0, 1, 2 đều có mặt.  Nếu r và s là các BTCQ thì: 
 Biểu thức đó thường được viết tắt là 0+1+2+. 4. L(r+s) = L (r)  L(s) 
  Ví dụ 3.8: Hãy xây dựng BTCQ xác định các chuỗi có chứa số 0 5. L(r.s) = L(r) L(s) 
 và 1 xen kẻ nhau. 6. L((r)) = L(r) 
 7. L(r*) = (L(r))* 
 47 48 
 12 
 Biểu thức chính qui (tt) Biểu thức chính qui (tt) 
 Các tính chất đại số của biểu thức chính qui: 
 Dễ dàng Giải thuật rằng, cho r, s, t là các biểu thức chính quy, thì ta có 
 các đẳng thức sau, trong đó r = s có nghĩa là L(r) = L(s).  Ví dụ 3.8: cho BTCQ r = a* . (a+b) 
  Tìm ngôn ngữ L(r) gồm tất cả các chuỗi được chỉ định 
 1. r + s = s + r 8. r = r =  
 bởi r. 
 2. r + r = r 9. r +  = r Giải 
 3. r + (s + t) = (r + s) + t 10. * =   Ta có L(r) = L(a*. (a+b)) = L(a*) L(a+b) 
  = (L(a))* (L(a)  L(b)) 
 4. r(st) = (rs)t 11.(+r)* = r* 
  = {an | n 0} {a,b} 
 5. r(s + t) = rs + rt 12. r + r* = r* 
  = {an+1, anb | n 0 } 
 6. (r + s)t = rt + st 13.(r*)* = r* 
 7. r = r =r 14.(r*s*)* = (r + s)*. 
 49 50 
 Biểu thức chính qui (tt) Liên quan giữa BTCQ và OH 
  Ví dụ 3.9: Cho BTCQ r = (aa)* (bb)*b 
 Biểu thị cho tập hợp tất cả các chuỗi sao cho có chẳn con chữ a theo sau 
 là lẻ con chữ b. Đó là  Bổ đề 3.4: Với mọi tập hữu hạn L  *, đều tồn tại một một 
 L(r) = {a2n b2m+1 | n,m 0 } BTCQ mà tập nó chỉ định là L. 
  Ví dụ 3.10: Cho  = {0,1}. Hãy xác định BTCQ r sao cho L(r) = {w * | 
 w có ít nhất một cặp số 0 liên tiếp }  Định lý 3.9: Một ngôn ngữ L được chỉ định bởi một BTCQ khi và 
 Phân tích: mỗi chuỗi w chứa tổi thiểu 00, trước và sau nó là tùy ý 0, 1 chỉ khi nó được đoán nhận bởi một Ôtômát hữu hạn. 
 điều được. 
 Ta đã biết một chuỗi tùy ý trên  = {0,1} được biểu thị bởi BTCQ là (0+1)* 
 hoặc (1+0)* điều đúng. 
 Vậy BTCQ cần tìm là r = (0+1)*00(1+0)* 
 Ghi chú: Thông thường có vô số các BTCQ cho bất lỳ một ngôn ngữ nào. 
 Nên kết quả tìm BTCQ không phải là duy nhất. 
 51 52 
 13 
 Thuật toán Thompson Thuật toán Thompson (tt) 
 Bài toán: Cho một biểu thức chính quy. Hãy xây dựng ôtômát 
  Sau đó áp dụng luật 1, luật 2 để xây dựng các ôtômát 
 hữu hạn không đơn định đoán nhận ngôn ngữ chính quy từ không đơn định M , M ,, M tương đương đoán nhận các 
 biểu thức chính quy đã cho. 1 2 k
 ngôn ngữ L(r1), L(r2), , L(rk). 
 Thuật toán:  Cuối cùng áp dụng luật 3 để xây dựng ôtômát không đơn 
  Vào: Một biểu thức chính quy r trên tập . định M đoán nhận ngôn ngữ L(r). 
  Ra: Một ôtômát hữu hạn không đơn định đoán nhận ngôn 
 ngữ L(r). • Luật 1: BTCQ r=, ngôn ngữ biểu thị cho nó là 
 L(r) = {}. Xây dựng OH đoán nhận L(r) như sau: 
 Sau đây là thuật toán Thompson: 
  Trước hết tách biểu thức chính quy r thành các biểu thức 
 Đầu  
 q q
 chính quy thành phần r1, r2,rk. 0 f 
 53 54 
 Thuật toán Thompson (tt) 
 Thuật toán Thompson (tt) 
 M(r) 
   
 • Luật 2: BTCQ r=a trên  ={a}, ngôn ngữ do nó sinh Đầu 
 ra là L(r)= {a}. Xây dựng OH đoán nhận L(r) như sau: i f 
   
 M(s) 
 Đầu a 
 q q
 0 f b. Đối với BTCQ (r).(s) thì OHK đoán nhận ngôn ngữ 
 L(r).L(s) như sau: 
 • Luật 3: Giả sử M(r), M(s) là các ôtômát thành 
 phần tương ứng với các BTCQ s và r: 
 Đầu M(r) M(s) 
 a. Với BTCQ (r)  (s) ta xây dựng OH đoán nhận i f 
 ngôn ngữ L(r)  L(s) như sau: 
 55 55 56 
 14 
 Thuật toán Thompson (tt) Bài tập: cho NNCQ xây dựng Ôtômát 
  Ví dụ 3.12: Xây dựng Ôtômát đoán nhận tất cả các chuỗi 
 c. Đối với BTCQ (r)* thì OHK đoán nhận ngôn ngữ (L(r))* 
 trên  = {a,b,0,1} sao cho kết thúc bởi ab 
 như sau: 
  
  Ví dụ 3.13: Xây dựng Ôtômát đoán nhận tất cả các chuỗi 
 thuộc {0, 1}* sao cho có chứa chuỗi con 01 đâu đó. 
 Đầu  M(r)  
 i f 
  Ví dụ 3.14: Xây dựng Ôtômát đoán nhận ngôn ngữ 
  L={aabna | n 0} 
 Ví dụ 3.11: Xây dựng NFA từ biểu thức chính quy: 01*+1 
 57 58 
 15