Bài giảng Lập và phân tích dự án cho kỹ sư - Chương 8: Rủi ro và bất định trong phân tích dự án - Nguyễn Ngọc Bình Phương
Chắc chắn/tất định (certainty) – khi biết khả
năng chắc chắn xuất hiện của các trạng thái.
Rủi ro (risk): khi biết được xác suất xuất hiện
của các trạng thái.
Không chắc chắn/bất định (uncertainty): khi
không biết được xác suất xuất hiện của các
trạng thái hoặc không biết được các dữ liệu liên
quan đến vấn đề cần giải quyết.
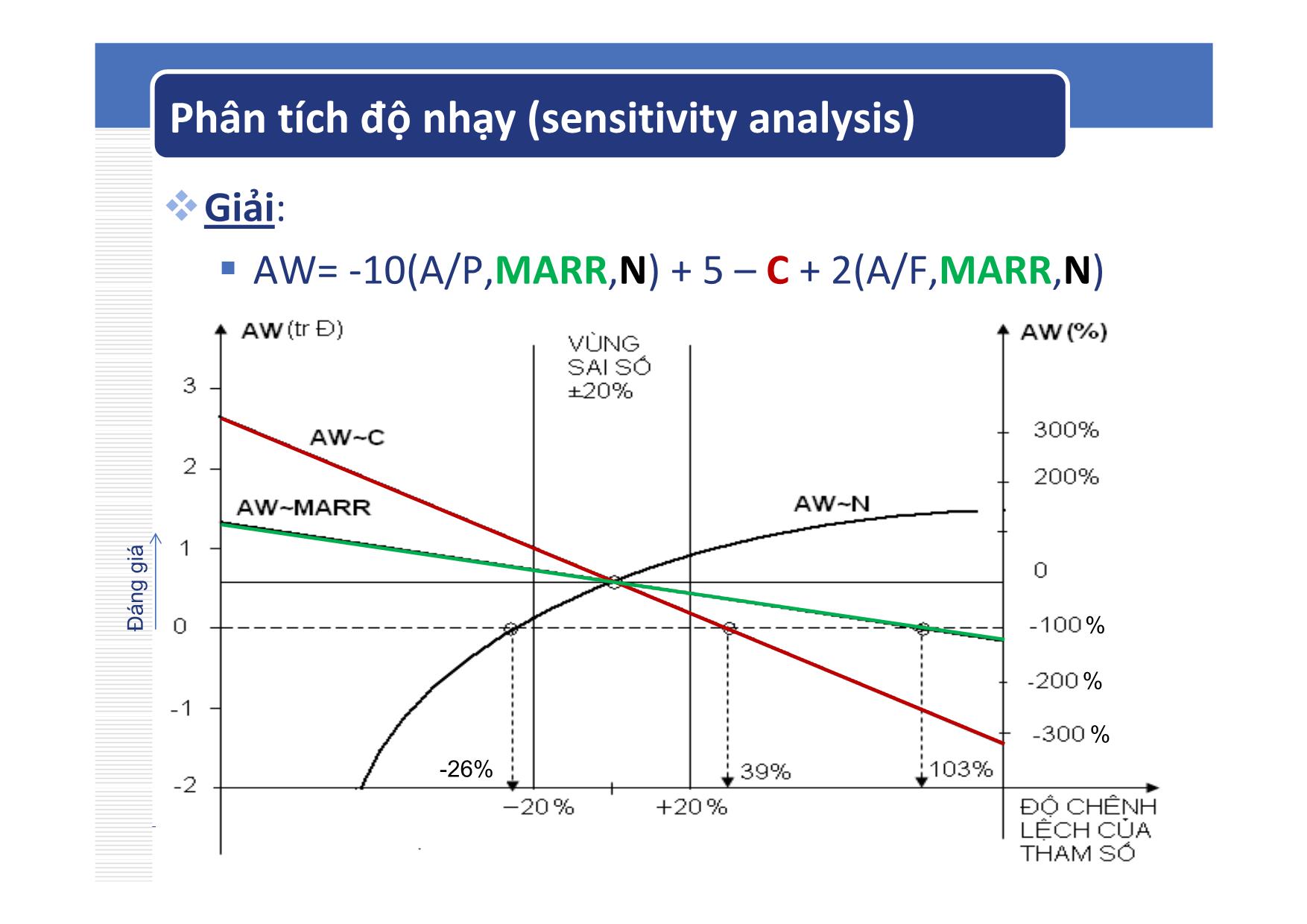
¾Cần phân biệt một số khái niệm

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Lập và phân tích dự án cho kỹ sư - Chương 8: Rủi ro và bất định trong phân tích dự án - Nguyễn Ngọc Bình Phương", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Lập và phân tích dự án cho kỹ sư - Chương 8: Rủi ro và bất định trong phân tích dự án - Nguyễn Ngọc Bình Phương

Chương 8 RỦI RO VÀ BẤT ĐỊNH TRONG PHÂN TÍCH DỰ ÁN Nguyễn Ngọc Bình Phương nnbphuong@hcmut.edu.vn Khoa Quản lý Công nghiệp Đại học Bách Khoa - TPHCM Nội dung 1. Tổng quan rủi ro và bất định 2. Phân tích độ nhạy (sensitivity analysis) 3. Phân tích rủi ro (risk analysis) bằng giải tích 2 Tổng quan rủi ro và bất định ¾Cần phân biệt một số khái niệm Chắcchắn/tất định (certainty) – khi biếtkhả năng chắcchắnxuấthiệncủacáctrạng thái. Rủiro(risk):khi biết đượcxácsuấtxuấthiện củacáctrạng thái. Không chắcchắn/bất định (uncertainty):khi không biết đượcxácsuấtxuấthiệncủacác trạng thái hoặc không biết đượccácdữ liệu liên quan đếnvấn đề cầngiải quyết. 3 Tổng quan rủi ro và bất định Xác suất khách quan: thông qua phép thử khách quan và suy ra xác suất Æ trong kinh tế, không có cơ hội để thử. Xác suấtchủ quan: Khi không có thông tin đầy đủ,ngườiraquyết định tự gán xác suấtmộtcách chủ quan đốivớikhả năng xuấthiệncủatrạng thái. Æ Không cầnthiếtphải phân biệtrủirovàbất định vì có thể gán xác suấtchủ quan vào phân tích bất định để trở thành phân tích rủiro. 4 Tổng quan rủi ro và bất định ¾Rủiroxảyracóthểảnh hưởng đến: 9Giá trị dòng tiềntệ (CF) vào và ra củadự án 9Suấtchiết tính (i) 9Tuổithọ (n) ⇒ Làm thay đổicáckếtquả thẩm định (PW, IRR, B/C ) 5 Tổng quan rủi ro và bất định Các phương thứchạnchế rủirovàbất định: 9Tăng cường độ tin cậycủathôngtinđầuvào, thựchiện đồng thời nhiềudự án khác nhau để san sẻ rủiro, 9Thựchiện các phân tích dựa trên các mô hình toán để làm cơ sở ra quyết định Nhóm mô hình mô tả (descriptive model) Nhóm mô hình có tiêu chuẩnhaycóđịnh hướng (normative or prescriptive model) 6 Tổng quan rủi ro và bất định Nhóm mô hình mô tả (descriptive model):môtả các đặctínhcủaphương án đầutư và xem xét những khả năng biến đổicóthể có của chúng Æ Từ mô hình này, ta chưacókếtluậncuốicùngmà chỉ có thông tin liên quan làm cơ sở cho việc ra quyết định. Ví dụ:xácđịnh giá trị hiệntạiPWcủamộtphương án Nhóm mô hình có tiêu chuẩnhaycóđịnh hướng (normative/prescriptive model):cóchứahàmmục tiêu cầnphải đạtcựctrị Æ Từ mô hình này, ta có đượckếtluậncuối cùng. Ví dụ: đặtmục tiêu giá trị PW đạtcực đại 7 Phân tích độ nhạy (sensitivity analysis) ¾Mục đích: Xem xét lạitínhkhả thi củadự án trong trường hợp mộtsố yếutố quan trọng ảnh hưởng lớn đếnkết quả thẩm định thay đổi. ¾Ví dụ: MARR (%) MARR thay đổi trong biên 16 độ ±5% thì PW thay đổinhư 14 thế nào? 12 10 Doanh thu hàng nămthay 8 đổi trong biên độ ±15% thì 6 PW thay đổinhư thế nào ? PW – 0 + 8 Phân tích độ nhạy (sensitivity analysis) Ví dụ:Cho dự án đầu tư mua máy tiện A với các tham số được ước tính như sau: Đầu tư ban đầu (P): 10 triệu đồng Chi phí hàng năm (C): 2,2 Thu nhập hàng năm (B):5,0 Giá trị còn lại (SV): 2,0 Tuổi thọ dự án (N): 5 năm Suất thu lợi tối thiểu (MARR): 8% Yêu cầu: Phân tích độ nhạy của AW lần lượt theo các tham số: N, MARR, C 9 Phân tích độ nhạy (sensitivity analysis) Giải: AW= -10(A/P,MARR,N) + 5 – C + 2(A/F,MARR,N) áng giá Đ % % % -26% Phân tích độ nhạy (sensitivity analysis) Phân tích độ nhạycủacácphương án so sánh: Khi so sánh 2 hay nhiềuphương án do dòng tiềntệ củacác phương án khác nhau nên độ nhạycủacácchỉ số hiệuquả kinh tếđốivớicácthamsố cũng khác nhau nên cầnphântích thêm sự thay đổinày Ví dụ:Có2phương án A và B cùng tuổithọ, độ nhạycủaPW theo tuổithọ Ncủa2phương án như sau: AtốthơnBkhiN>10năm Btốthơn A khi 7<N<10 năm A&B đều không đáng giá khi N<7 năm11 Phân tích độ nhạy (sensitivity analysis) Nhược điểmcủa phân tích độ nhạy: ¾Chỉ xem xét tác động củatừng tham số riêng lẻ (trong khi kếtquả thẩm định lạichịu tác động của nhiềuthamsố cùng lúc) ¾Không trình bày đượcxácsuất xuấthiệncủa các tham số và xác suấtxảyracủacáckếtquả Æ Phân tích tình huống (scenario analysis) sẽ phân tích độ nhạy nhiềuthamsố có liên quan Æ Phân tích rủi ro (risk analysis) sẽ khắcphục cả hai nhược điểmnày 12 Phân tích độ nhạy (sensitivity analysis) Phân tích độ nhạy theo nhiềuthamsố (scenario analysis – phân tích tình huống): ¾Mục đích:sosánhtrường hợp“cơ sở”(kỳ vọng) vớimột hay nhiềutrường hợpkhác(tốtnhất, xấunhất) để xác định các kếtquả thẩm định khác nhau củadự án. Tham số có thể Trường hợp Trường hợp Trường hợp thay đổigiátrị xấu nhất kỳ vọng tốt nhất Số lượng sp 1,600 2,000 2,400 Giá bán ($) 48 50 53 CP biến đổi ($) 17 15 12 CP cốđịnh ($) 11,000 10,000 8,000 Giá trị còn lại($) 30,000 40,000 50,000 PW (15%) -$5,856 $40,169 $104,295 13 Phân tích độ nhạy (sensitivity analysis) Phân tích độ nhạy theo nhiềuthamsố (scenario analysis – phân tích tình huống): A B 450 14 Phân tích độ nhạy (sensitivity analysis) ¾ Phân tích What-If trên Excel Một ví dụ đơn giản (dùng Data Table): Một người kinh doanh một mặt hàng A có giá mua là $8 và giá bán là $10. Giá mua biến động từ 4 đến 13, xét độ nhạy của lợi nhuận Giá mua biến động từ 4 đến 13 và giá bán biến động từ 6 đến 14, xét độ nhạy của lợi nhuận Một ví dụ đơn giản (dùng Scenario Manager): Một người kinh doanh một mặt hàng A có giá mua là $8 và giá bán là $10. Kết quả khảo sát nhận thấy giá mặt hàng A có thay đổi như sau: Giá mua Giá bán Tính lợi Trường hợp xấu nhất136 nhuận Trường hợp kỳ vọng 8 10 Trường hợp tốt nhất414 15 Phân tích rủi ro (risk analysis) bằng giải tích Định nghĩa: Là phân tích mô tả các ảnh hưởng đốivới độ đohiệuquả kinh tế củacácphương án đầutư trong điều kiệncórủiro. Mô hình tổng quát của bài toán phân tích rủi ro Trạng thái Phương án S1 S2 Sj Sn A1 R11 R12 R1j R1n A2 R21 R22 R2j R2n Ai Ri1 Ri2 Rij Rin Am Rm1 Rm2 Rmj Rmn Xác suấtcủatrạng thái P1 P2 Pj Pn Ai: Phương án đầu tư Si: Trạng thái xảy ra (khó khăn, thuận lợi) Rij: Chọnphương án Ai và trạng thái Sj xảy ra thì được kếtquả là Rij Pi: Xác suất để trạng thái Sj xảyra 16 (nếu bất định thì không xác định đượcPi) Phân tích rủi ro (risk analysis) bằng giải tích Giá trị kỳ vọng (expected value): kết quả trung bình của dự án Ai n = EA()iijj∑ ( R *) P j=1 Độ lệch chuẩn (standard deviation): đo mức độ rủi ro của dự án, cho biết kết quả lệch xa giá trị kỳ vọng E(Ai) bao nhiêu n σ =−2 ()Aiijij∑ (REAP ())* j=1 Hệ số biến thiên Cv (coefficient of variation): đo rủi ro tương đối giữa các dự án, dự án nào có Cv càng lớn thì mức độ rủi ro càng cao σ = ()Ai CV EA()i 17 Phân tích rủi ro (risk analysis) bằng giải tích Trạng thái S S S S Phương án 1 2 j n A1 R11 R12 R1j R1n A2 R21 R22 R2j R2n Ai Ri1 Ri2 Rij Rin A m Rm1 Rm2 Rmj Rmn Xác suấtcủatrạng thái P1 P2 Pj Pn R * P R * P + ..+ R * P + R * P EA()1 = 11 1 + 12 2 1j j 1n n σ 2 2 2 ()A1 = (R11- E(A1)) *P1 +(R12- E(A1)) *P2 +...+ (R1n- E(A1)) *Pn σ = ()A1 Cv EA()1 18 Phân tích rủi ro (risk analysis) bằng giải tích Ví dụ: 1 công ty xem xét suất thu lợi (IRR) của3 phương án A1, A2, A3 và các tình trạng kinh doanh có thể xảy ra là khó khăn, trung bình và thuận lợi cùng với các xác suất xảy ra tương ứng. Yêu cầu: Xác định kỳ vọng, mức độ rủi ro và hệ số biến hóa của các phương án Trạng thái Phương án Khó khăn Trung bình Thuận lợi A1 1% 4% 7% A2 -1% 4% 9% A3 -6% 4% 14% Xác suất trạng thái 25% 50% 25% Ghi chú: Đây là các phương án về đòn bẩy tài chính DE/V = 0; 0,4; 0,7 19 Phân tích rủi ro (risk analysis) bằng giải tích Trạng thái Khó khăn Trung bình Thuận lợi Phương án 1 % 4 % 7 % A1 -1 % 4 % 9 % A2 -6 % 4 % 14 % A3 Xác suất trạng thái 25 % 50 % 25 % = 0.01 *0.25 ++0.04 * 0.5 0.07 * 0.25 = 4% EA()1 ++ E()A2 = -0.01 *0.25 0.04 * 0.5 0.09 * 0.25 = 4% EA()3 = -0.06 *0.25 ++0.04 * 0.5 0.14 * 0.25 = 4% σ 2 ++2 2 ()A1 = (0.01 – 0.04) *0.25 (0.04 – 0.04) * 0.5 (0.07 – 0.04) * 0.25 = 2.12 % σ 2 ++2 2 ()A2 = (-0.01 – 0.04) *0.25 (0.04 – 0.04) * 0.5 (0.09 – 0.04) * 0.25 = 3.54 % σ (-0.06 – 0.04)2*0.25 ++(0.04 – 0.04)2* 0.5 (0.14 – 0.04)2 * 0.25 = 7.07 % ()A3 = 2.12 % 3.54 % 7.07 % 0.53 CA()= = 0.88 CA()= = 1.77 CAV()1 = = V 2 V 3 4 % 4 % 4 % 20 CAV ()3 Max Æ Phương án A3 có độ rủi ro cao nhất Phân tích rủi ro (risk analysis) bằng giải tích ¾ Tính xác suất theo phân phối chuẩn (normal distribution) Biến ngẫu nhiên X được gọi là tuân theo phân phối chuẩn nếu hàm mật độ xác suất có dạng: −−()x μ 2 1 2 fx()= e 2σ σπ2 μ là kỳ vọng (trung bình) củabiếnngẫu nhiên X EX()= μ σ 2 là phương sai củabiếnngẫu nhiên X 2 Var() X = σ σ là độ lệch chuẩn củabiếnngẫu nhiên X 21 Phân tích rủi ro (risk analysis) bằng giải tích ¾ Tính xác suất theo phân phối chuẩn (normal distribution) Ký hiệu : XN~(,μ σ 2 ) (phân phối chuẩn) Z ~(0,1)N (phân phối chuẩn hóa/tắc) (standard distribution) P(a<X<b) = S b −−()x μ 2 1 2 Sedx= 2σ σπ∫ 2 a 22 Phân tích rủi ro (risk analysis) bằng giải tích ¾ Tính xác suất theo phân phối chuẩn (normal distribution) X − μ 2 Đặt Z = XN~(,μσ )⇒ ZN ~(0,1) σ ⇒Pa()(<<= X b Pa <σ Z +<μ b ) ab−−μμba−−μμ =<<PZ()=<PZ()() −< PZ σσ σσ ⎛⎞⎛⎞⎛⎞⎛⎞ba−−μμ b − μ a − μ =−=Φ−ΦFF⎜⎟⎜⎟⎜⎟⎜⎟ ⎝⎠⎝⎠⎝⎠⎝⎠σσ σ σ f(z) � � S = Φ(z) �� �� 1 � 1 � � z= � � � �� ; Φ z= � � � �� 2π 2π S �∞ � z 0 Φ(z): Hàm Laplace (dùng bảng tra) zo 23 f(z) S z 0 zo 24 Phân tích rủi ro (risk analysis) bằng giải tích ¾ Tính xác suất theo phân phối chuẩn (normal distribution) Ví dụ:Tìmxácsuất để phương án đầutư A1 (ví dụ trước) có suấtthulợi (IRR) sau thuế nằmtrongkhoảng: μ == a) 4% đến5% Biết EA()4%1 b) 5% đến6% σσ== (A1 ) 2,12% Giải: −− << =Φ⎛⎞⎛⎞5% 4% −Φ 4% 4% aP) (4% RR 5%) ⎜⎟⎜⎟ ⎝⎠⎝⎠2,12% 2,12% =Φ(0,47) −Φ (0) = 18,08% − 0 = 18,08% −− << =Φ⎛⎞⎛⎞6% 4% −Φ 5% 4% bP) (5% RR 6%) ⎜⎟⎜⎟ ⎝⎠⎝⎠2,12% 2,12% =Φ()()0.94 −Φ 0.47 = 32,64% − 18,08% = 14,56% 25 Phân tích rủi ro (risk analysis) bằng giải tích ¾ Phân tích rủi ro trong dòng tiền CF + Giá trị hiện tại của dòng �ền: N =+− j PW∑(1 i ) Aj j=0 + Kỳ vọng giá trị hiện tại của dòng �ền: N =+− j EPW()∑ (1)() i EAj j=0 + Phương sai giá trị hiện tại của dòng �ền: N ==+σ 22− j Var() PW () PW∑ (1) i Var () Aj j=0 26 Phân tích rủi ro (risk analysis) bằng giải tích ¾ Phân tích rủi ro trong dòng tiền CF + Độ lệch chuẩn giá trị hiện tại của dòng �ền: Là giá trị biểu thị mức độ rủi ro của dự án. N σ =+−2 j ()PW∑ (1) i Var () Aj j=0 + Định lý giới hạn trung tâm (Central Limit Theorem): Khi N tăng lớn, PW sẽ tuân theo phân phối chuẩn có kỳ vọng là E(PW) và phương sai là Var(PW): NPWNEPWVarPW→∞⇒ ~,()() () 27 Phân tích rủi ro (risk analysis) bằng giải tích ¾ Phân tích rủi ro trong dòng tiền CF Ví dụ:Mộtcôngty dự định đầutư vào mộtdây chuyền sản xuất với: P = 2.000 tr – vốn đầutư (xem như biết chắc chắn) A = 1.000 tr – thu nhập ròng trung bình hàng năm(xem thu nhập ròng mỗinămlàcácbiếnngẫunhiên độc lập tuân theo phân phốichuẩnvới độ lệch chuẩnlà200 tr) N=3năm MARR = 10% SV = 0 Yêu cầu: Tính xác suất để PW < 0 (tứcdự án không đáng giá) 28 Phân tích rủi ro (risk analysis) bằng giải tích ¾ Phân tích rủi ro trong dòng tiền CF N 3 − =+− j = ++()j EPW()∑∑ (1)()() i EAj EA0 10,1() EAj jj==013 =−2000 +∑ 1000(1 + 10%)− j =− 2000 + 1000(PA / ,10%,3) j=1 =−2000 + 1000*2,4869 = 486,9 tr N − ==+σ 2 () ()2 j () Var() PW PW∑ 1 i Var Aj j=0 N − j 3 − =+++=++()2 () ()j Var( A0 )∑∑ 1 2 i i Var Aj 0 40000 1 21% jj==11 ==40000(PA / ,21%,3) 82.957 29 Phân tích rủi ro (risk analysis) bằng giải tích ¾ Phân tích rủi ro trong dòng tiền CF σ ()PW= Var() PW = 82957 = 288 tr EPW()= 487 tr Giả sử PW tuân theo quy luật phân phối chuẩn: PW~(487,288) N 2 Xác suất để PW có giá trị âm: ⎛⎞0− 487 PPW(0)<= P⎜⎟ Z < ⎝⎠288 =<−=−=Φ−−Φ−∞PZ( 1.69) F ( 1.69) ( 1.69) ( ) = -0.4545 + 0.5 = 4.55% (tra bảng) 30 HẾT CHƯƠNG 8 31
File đính kèm:
 bai_giang_lap_va_phan_tich_du_an_cho_ky_su_chuong_8_rui_ro_v.pdf
bai_giang_lap_va_phan_tich_du_an_cho_ky_su_chuong_8_rui_ro_v.pdf

