Bài giảng Kỹ thuật lập trình - Chương 6: Kỹ thuật đệ quy

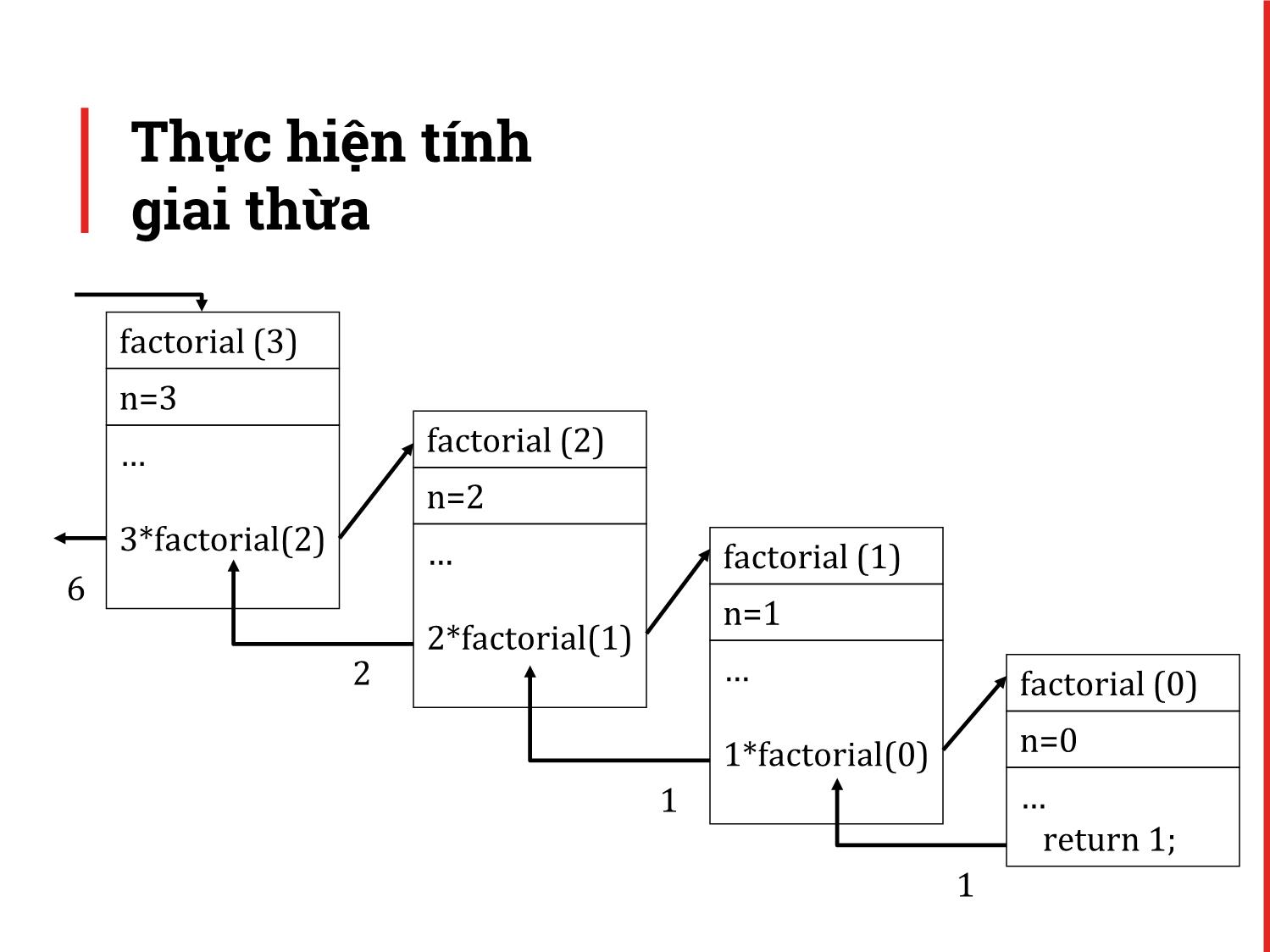
 khi tính giai thừa
 Stack hệ thống
 factorial(0)
 factorial(1) factorial(1) factorial(1)
 factorial(2) factorial(2) factorial(2) factorial(2) factorial(2)
 factorial(3) factorial(3) factorial(3) factorial(3) factorial(3) factorial(3) factorial(3)
 t
 Thời gian hệ thống
 Trả về từ Trả về từ Trả về từ Trả về từ 
Gọi hàm Gọi hàm Gọi hàm Gọi hàm hàm hàm hàm hàm
factorial(3) factorial(2) factorial(1) factorial(0) factorial(0 factorial(1 factorial(2 factorial(3
 ) ) ) )
 t
 Thành phần của 
 mô tả đệ quy
▪ Phần neo: trường hợp suy biến của đối tượng
 ▫ Ví dụ: 1 là số tự nhiên, cấu trúc rỗng là danh sách kiểu T, 0!=1, 
 SM (a[x:x]) là thao tác rỗng.
▪ Phần qui nạp: mô tả đối tượng (giải thuật) thông qua chính
đối tượng (giải thuật) đó một cách trực tiếp hoặc gián tiếp.
 Ví dụ:
 ▫ n! = n * (n –1)!
 ▫ SM (a[m:n]) ≡Merge (SM (a[m:( m+n) div 2] , SM (a[(m+n) div 2 
 +1 : n]) )
Phân loại
đệ quy
Đệ quy trực tiếp Đệ quy gián tiếp
▸Đệ quy tuyến tính ▸Đệ quy hỗ tương
▸Đê qui nhị phân
▸Đệ quy phi tuyến
 KieuDuLieu TenHam(Thamso)
 {
 if(Dieu Kien Dung)
 {
 Đệ quy ...;
 return Gia tri tra ve;
 }
 tuyến tính ...;
 TenHam(Thamso)
 ...;
▪ Là đệ quy có dạng }
 P( ) { 
 If (B) thực hiện S;
 else { thực hiện S* ; gọi P }
 } 
 Với S , S* là các thao tác không đệ quy. 
▪ VD: Hàm FAC(n) tính số hạng n của dãy n!
 int FAC( int n ) 
 {
 if ( n == 0 ) return 1 ; 
 else return ( n * FAC(n-1 )) ; 
 } 
Ví dụ Tính 
 S(n) = 1/(1*2) + 1/(2*3) + ... + 1/( n*(n+1) )
 S(n) = 1/2 khi n==1
 = S(n-1)+1/(n*(n+1))
 float S(int n) {
 if ( n==1) return 0.5;
 else return S(n-1)+1.0/(n*(n+1));
 }
 KieuDuLieu TenHam(Thamso)
 {
 if(Dieu Kien Dung)
 {
 Đệ quy ...;
 return Gia tri tra ve;
 }
 nhị phân ...;
 TenHam(Thamso);
 ...;
▪ Là đệ quy có dạng TenHam(Thamso);
 P ( ) { ...;
 If (B) thực hiện S; }
 else { 
 thực hiện S*; 
 gọi P ; gọi P;
 }
 } 
 Với S , S* là các thao tác không đệ quy. 
▪ Ví dụ: Hàm FIBO(n) tính số hạng n của dãy FIBONACCI
 int F(int n) { 
 if ( n < 2 ) return 1; 
 else 
 return (F(n -1) + F(n -2)); 
 } 
Ví dụ Tính tổng các giá trị của dãy số H(n), biết
 H(n) = n khi n<3
 = 2*H(n-1)*H(n-2) khi n>2
 long H(int n) {
 if (n<3) return n;
 else return 2*H(n-1)*H(n-2);
 }
 long Tong(int n) {
 long tg=0;
 for( int i=1; i<=n;i++) 
 tg+=H(i);
 return tg;
 }
 KieuDuLieu TenHam(Thamso)
 {
 if(Dieu Kien Dung)
 {
 Đệ quy ...;
 return Gia tri tra ve;
 }
 phi tuyến ...;
 vonglap(dieu kien lap)
 {
 ...TenHam(Thamso)...;
 }
 return Gia tri tra ve;
 }
▪ Là đệ quy mà lời gọi đệ quy được thực hiện bên trong vòng
lặp.
 P ( ) {
 for ( to ) {
 thực hiện S ;
 if (điều kiện dừng) then thực hiện S*;
 else gọi P;
 } 
 }
 Với S , S* là các thao tác không đệ quy. 
 Đệ quy
 phi tuyến
▪ Ví dụ: Cho dãy { An } xác định theo công thức truy hồi :
 A0= 1 ; 
 2 2 2 2
 An = n A0+(n-1) A1+ . . . + 2 An-2+ 1 An-1
 int A( int n ) {
 if (n==0) return 1 ; 
 else { 
 int tg = 0 ; 
 for (int i=0; i<n; i++) 
 tg = tg + sqr(n-i) *A(i); 
 return tg; 
 } 
 }
 KieuDuLieu TenHamX(Thamso)
 {
 if(Dieu Kien Dung)
 {
 Đệ quy ...;
 return Gia tri tra ve;
 }
 tương hỗ ...;
 return TenHamX(Thamso) <Lien
 ket hai ham> TenHamY(Thamso);
▪ Là một loại đệ quy gián }
tiếp
 KieuDuLieu TenHamY(Thamso)
▪ Trong đệ quy tương hỗ {
 if(Dieu Kien Dung)
có 2 hàm, và trong thân {
của hàm này có lời gọi ...;
 return Gia tri tra ve;
của hàm kia, điều kiện }
 ...;
dừng và giá tri trả về return TenHamY(Thamso)<Lien 
của cả hai hàm có thể 
 ket hai ham>TenHamX(Thamso);
giống nhau hoặc khác }
nhau
 X(n) = 1,2,3,5,11,41
Ví dụ Y(n) = 1,1,2,6,30,330 ..
 void main() {
 int n;
 printf("\n Nhap n = ");
 scanf("%d",&n);
 printf( "\n X = %d " ,X(n));
 printf( "\n Y = %d " , Y(n));
 getch();
 }
 long Y(int n); //prototype cua ham y
 long X(int n) {
 if(n==0) 
 return 1;
 else
 return X(n-1) + Y(n-1);
 }
 long Y(int n) {
 if(n==0)
 return 1;
 else
 return X(n-1)*Y(n-1);
 }
 Tìm giải thuật
 đệ quy
1. Thông số hóa bài toán .
 ▫ Tổng quát hóa bài toán cụ thể cần giải thành bài toán tổng
 quát (một họ các bài toán chứa bài toán cần giải )
 ▫ Tìm ra các thông số cho bài toán tổng quát
 ▸ các thông số điều khiển: các thông số mà độ lớn của chúng đặc
 trưng cho độ phức tạp của bài toán , và giảm đi qua mỗi lần gọi đệ 
 quy.
 ▸ Vídụ
 ▸ n trong hàm FAC(n) ; 
 ▸ a , b trong hàm USCLN(a,b) .
 Tìm giải thuật
 đệ quy
2. Tìm các trường hợp neo cùng giải thuật giải tương ứng
 ▫ trường hợp suy biến của bài toán tổng quát
 ▫ các trường hợp tương ứng với các gía trị biên của các biến điều
 khiển
 ▫ VD: FAC(1) =1
 USCLN(a,0) = a
3. Tìm giải thuật giải trong trường hợp tổng quát bằng phân
 rã bài toán theo kiểu đệ quy
 Tìm giải thuật
 đệ quy
▪ Phân rã bài toán tổng quát theo phương thức đệ quy
 ▫ Tìm phương án (giải thuật ) giải bài toán trong trường hợp 
 tổng quát phân chia nó thành các thành phần
 ▸ giải thuật không đệ quy
 ▸ bài toán trên nhưng có kích thước nhỏ hơn.
 ▫ Vídụ
 FAC(n) = n * FAC(n -1) .
 Tmax(a[1:n]) = max(Tmax(a[1:(n-1)]) , a[n] ) 
 Bài toán 
 Tháp Hà Nội
▪ Luật:
 ▫ Di chuyển mỗi lần một đĩa
 ▫ Không được đặt đĩa lớn lên trên đĩa nhỏ
 n
 Với chồng gồm n đĩa cần 2 -1 lần chuyển
 –Giả sử thời gian để chuyển 1 đĩa là t giây thì thời gian để
 chuyển xong chồng 64 đĩa sẽ là:
 –T = ( 2^64-1) * t = 1.84 * 10^19 t
 –Với t = 1/100 s thì T = 5.8*10^9 năm = 5.8 tỷ năm .
 Bài toán 
 Tháp Hà Nội
▪ Hàm đệ quy: Chuyển n đĩa từ A sang C qua trung gian B
 ▫ Chuyển n-1 đĩa trên đỉnh của cột A sang cột B
 ▫ Chuyển 1 đĩa (cuối cùng) của cột A sang cột C
 ▫ Chuyển n-1 đĩa từ cột B sang C qua tg A
 magic
 Bài toán 
 Tháp Hà Nội
▪ Thông số hóa bài toán
 ▫ Xét bài toán ở mức tổng quát nhất: chuyển n (n>=0) đĩa từ cột A 
 sang cột C lấy cột B làm trung gian .
 ▫ THN(n,A,B,C) -> với 64 đĩa gọi THN(64,A,B,C)
 ▫ n sẽ là thông số quyết định bài toán –n là tham số điều khiển
▪ Trường hợp suy biến và cách giải
 ▫ Với n =1 : THN (1,A,B,C) 
Giải thuật giải bt THN (1,A,B,C) là thực hiện chỉ 1 thao tác cơ bản: Chuyển
1 đĩa từ A sang C (ký hiệu là Move (A , C))
 ▸ THN(1,A,B,C) ≡ { Move( A, C ) } 
 ▸ THN(0,A,B,C) ≡ { φ} 
 Bài toán 
 Tháp Hà Nội
▪ Bài toán THN (k,A,B,C): chuyển k đĩa từ cột A sang cột C lấy
cột B làm trung gian
 1. Chuyển (k -1) đĩa từ cột A sang cột B lấy cột C làm trung gian
 THN (k -1,A,C,B) (bài toán THN với n = k-1,A= A , B = C , C = B )
 2. Chuyển 1 đĩa từ cột A sang cột C : Move ( A, C ) (thao tác cơ
 bản ).
 3. Chuyển (k - 1 ) đĩa từ cột B sang cột C lấy cột A làm trung gian
 THN( k -1,B,A,C) ( bài toán THN với n = k-1 , A = B , B = A , C = C ) 
Giải thuật 
tổng quát
 Với n>1
 THN(n,A,B,C) ≡
 {
 THN (n -1,A,C,B) ; 
 Move ( A, C ) ; 
 THN (n -1,B,A,C) ; 
 }
Code
 void move(int n, int A, int B, int C) {
 if (n > 0) {
 move(n − 1, A, C, B);
 printf("\n Move disk % d from %c to % c ",
 n, A,C );
 move(n − 1, B, A, C);
 }
 }
 Bài toán 
 chia phần thưởng
▪ Có 100 phần thưởng đem chia cho 12 học sinh giỏi đã
được xếp hạng. Có bao nhiêu cách khác nhau để thực hiện
cách chia?
▪ Tìm giải thuật giải bài toán bằng phương pháp đệ quy.
 Bài toán
 chia phần thưởng
▪ Nhìn góc độ bài toán tổng quát: Tìm số cách chia m vật
(phần thưởng) cho n đối tượng (học sinh ) có thứ tự. 
 ▫ PART(m ,n)
 ▫ N đối tượng đã được sắp xếp 1,2,,n
 ▫ Si là số phần thưởng mà i nhận được
 Si>= 0 
 S1>= S2>=  >= Sn. 
 S1+ S2+ ...+ Sn = m 
 ▫ Ví dụ:
 Với m = 5 , n = 3 ta có 5 cách chia sau :
 5 0 0 ,4 1 0, 3 2 0 ,3 1 1 ,2 2 1 
 Tức là PART(5,3) = 5
 Bài toán
 chia phần thưởng
▪ Các trường hợp suy biến
 ▫ m = 0 : mọi học sinh đều nhận được 0 phần thưởng .
 PART(0 , n ) = 1 với mọi n
 ▫ n = 0 , m 0 : không có cách chia
 PART(m , 0 ) = 0 với mọi m 0 .
 Bài toán
 chia phần thưởng
▪ Phân rã bài toán trong trường hợp tổng quát
 ▫ m < n : n -m học sinh xếp cuối sẽ luôn không nhận được gì cả
 trong mọi cách chia .
 Vậy: n > m thìPART(m , n ) = PART(m , m )
 ▫ m>=n: là tổng
 ▸ Học sinh cuối cùng không có phần thưởng
 ▸ PART(m , n -1 ) 
 ▸ Học sinh cuối cùng có ít nhất 1
 ▸ PART(m -n , n ) 
 ▸ Vậy: m > n => PART(m , n ) = PART(m , n -1 ) + PART(m -n , n )
 Bài toán
 chia phần thưởng
▪ Dạng hàm PART trong C++
 int PART(int m, int n) 
 { 
 if ((m == 0) || (n == 0) ) return 1 ; 
 else if(m < n) return (PART(m, m)); 
 else 
 return (PART(m, n -1) + PART(m -n, n));
 } 
▪ Kết quả sai?
 Khử
 đệ quy
Đệ quy
o Ưu điểm: gọn gàng, dễ
 hiểu, dễ viết code
o Nhược điểm: tốn không
 gian nhớ và thời gian xử
 lý
 Thay thế bằng giải 
 thuật không đệ quy
 Khử 
 đệ quy
▪ Sơ đồ để xây dựng chương trình cho một bài toán khó khi ta
không tìm được giải thuật không đệ quy thường là:
 ▫ Dùng quan niệm đệ quy để tìm giải thuật cho bài toán .
 ▫ Mã hóa giải thuật đệ quy.
 ▫ Khử đệ quy để có được một chương trình không đệ quy .
▪ Tuy nhiên, khử đệ quy không phải bao giờ cũng dễ => trong
nhiều trường hợp ta cũng phải chấp nhận sử dụng chương
trình đệ quy
 Khử đệ quy bằng
 vòng lặp
▪ Giải thuật hồi qui thường gặp
 f(n) = C khi n = no (C là một hằng)
 = g(n,f(n -1)) khi n > no
▪ Ví dụ:
 ▫ Hàm giai thừa FAC (n) = n! = 1 khi n=0
 = n*FAC(n -1) khi n>0
 ▫ Tổng n số đầu tiên của dãy đan dấu sau :
 Sn = 1 -3 + 5 -7 .. + (-1)^(n+1) * (2n-1) 
 S(k) = 1 khi k =1 
 = S(k-1) + (-1)^(k+1)*(2*k-1) với k > 1
 Khử đệ quy bằng
 vòng lặp
▪ Giải thuật đệ quy tính giá trị f(n) 
 f(n) ≡ if(n == no) return C; 
 else return (g(n,f(n -1)); 
▪ Giải thuật lặp tính giá trị f(n)
 K = no; F:= C; 
 { F = f(no) } 
 While( k < n ){
 k += 1; 
 F = g(k,F); 
 }
 return F;
▪ Khử đệ quy với hàm tính giai thừa
 int FAC ( int n ) { 
 int k = 0; 
 int F = 1; 
 while ( k < n ) F = ++k * F; 
 return (F); 
 }
▪ Khử đệ quy với hàm tính S(n)
 int S ( int n ) {
 int k = 1 , tg = 1 ; 
 while ( k < n ) { 
 k ++ ; 
 if (k%2 == 1) tg + = 2 * k -1; 
 else tg -= 2 * k + 1 ; 
 }
 return ( tg ) ; 
 }
 Đệ quy dạng
 đệ quy đuôi
▪ Xét thủ tục P dạng
 P(X) ≡ if B(X) then D(X) 
 else { 
 A(X) ; 
 P(f(X)) ; 
 } 
▪ Trong đó: 
 ▫ X là tập biến (một hoặc một bộ nhiều biến)
 ▫ P(X) là thủ tục đệ quy phụ thuộc X
 ▫ A(X); D(X) là các thao tác không đệ quy
 ▫ f(X) là hàm biến đổi X
 Đệ quy dạng
 đệ quy đuôi
▪ Xét quá trình thi hành P(X) :
 ▫ gọi Po là lần gọi P thứ 0 (đầu tiên) P(X)
 ▫ P1 là lần gọi P thứ 1 (lần 2) P(f(X))
 ▫ Pi là lần gọi P thứ i (lần i + 1) P(f(f(...f(X)...)
 ▫ ( P(fi(X)) hợp i lần hàm f )
▪ Gọi Pi nếu B(fi(X))
 ▫ (false) { A và gọi Pi+1 } 
 ▫ (true) { D }
▪ Giả sử P được gọi đúng n +1 lần . Khi đó ở trong lần gọi cuối
cùng (thứ n ) Pn thì B(fn(X)) = true, lệnh D được thi hành và
chấm dứt thao tác gọi thủ tục P 
 ▪Sơ đồ thực hiện giải thuật trên
Đệ quy dạng bằng vòng lặp
đệ quy đuôi
 While (!B(X)) 
 {
 A(X); 
 X = f(X); 
 }
 D(X); 
Ví dụ
Tìm ước chung lớn nhất
Giải thuật đệ quy Khử đệ quy
int USCLN(int m, int n) { int USCLN(int m , int n ) 
 if (n == 0) return m; {
 else USCLN(n, m % n); while(n != 0 ) { 
} int sd = m % n ; 
 m = n ; 
▪X là( m , n ) n = sd ; 
▪P(X) là USCLN(m ,n) } 
▪B(X) là n == 0
▪D(X) là lệnh return m return (m) ; 
▪A(X) là lệnh rỗng } 
▪f(X ) là f(m,n) = ( n , m mod n ) 
 Khử đệ quy bằng 
 stack
▪ Trạng thái của tiến trình xử lý một giải thuật: nội dung các biến
và lệnh cần thực hiện kế tiếp.
▪ Với tiến trình xử lý một giải thuật đệ quy ở từng thời điểm thực
hiện, cần lưu trữ cả các trạng thái xử lý đang còn dang dở
▪ Xét giải thuật giai thừa
 FAC ( n ) ≡ if(n = 0 ) then return 1; 
 else return ( n * FAC (n –1));
▪ Sơ đồ thực hiện
Thủ tục đệ quy tháp Hà Nội THN (n , A , B , C) 
 THN (n : integer ; A ,B , C : char) ≡ {
 if (n > 0 ) then { THN(n-1,A ,C ,B); 
 Move(A, C); THN(n-1,B,A,C);} }
Sơ đồ thực hiện THN(3,A,B,C)
 Khử đệ quy bằng 
 stack
▪ Lời gọi đệ quy sinh ra lời gọi đệ quy mới cho đến khi gặp trường 
hợp suy biến (neo) 
▪ Ở mỗi lần gọi, phải lưu trữ thông tin trạng thái con dang dở của
tiến trình xử lý ở thời điểm gọi. Số trạng thái này bằng số lần gọi
chưa được hoàn tất.
▪ Khi thực hiện xong (hoàn tất) một lần gọi, cần khôi phục lại toàn
bộ thông tin trạng thái trước khi gọi .
▪ Lệnh gọi cuối cùng (ứng với trương hợp neo) sẽ được hoàn tất
đầu tiên
▪ Cấu trúc dữ liệu cho phép lưu trữ dãy thông tin thỏa 3 yêu cầu
trên là cấu trúc lưu trữ thỏa mãn LIFO (Last In First Out ~ Cấu trúc
stack)
 Chủ động tạo cấu trúc 
 stack chuyên dụng
 Đệ quy chỉ có một
 lệnh gọi trực tiếp
▪ Đệ quy có dạng sau:
 P(X) ≡ if C(X) then D(X) 
 else begin 
 A(X) ; 
 P(f(X)) ; 
 B(X) ; 
 end; 
 ▫ X là một biến đơn hoặc biến véc tơ.
 ▫ C(X) là một biểu thức boolean của X .
 ▫ A(X) , B(X) , D(X): không đệ quy
 ▫ f(X) là hàm của X 
 Đệ quy chỉ có một
 lệnh gọi trực tiếp
▪ Giải thuật thực hiện P(X) với việc sử dụng Stack có dạng
P(X) ≡ { 
 Create_Stack (S); ( tạo stack S )
 While(not(C(X)) do begin 
 A(X); 
 Push(S,X); ( cất gía trị X vào stack S )
 X := f(X); 
 end; 
 D(X); 
 While(not(EmptyS(S))) do begin 
 POP(S,X); ( lấy dữ liệu từ S )
 B(X); 
 end; 
} 
 Ví dụ
 Chuyển từ cơ số thập phân sang nhị phân
Đệ quy Khử đệ quy
Binary(m) ≡ if ( m > 0 ) Binary (m) ≡ {
then begin Create_Stack(S); 
 Binary( m / 2 ) ; While ( m > 0 ) do begin 
 write( m % 2 ) ; sdu = m % 2 ; 
end; Push(S,sdu) ; 
 m = m / 2 ; 
Trong đó end; 
▫X là m . While(not(EmptyS(S)) do begin 
▫P(X) là Binary(m) . POP(S,sdu) ; 
▫A(X) ; D(X) là lệnh rỗng . Write(sdu) ; 
▫B(X) là lệnh Write(m % 2 ) ;
 end; 
▫C(X) là ( m <= 0 ) .
▫f(X) = f(m) = m / 2 } 
 Đệ quy với
 2 lần gọi đệ quy
▪ Đệ quy có dạng sau
 P(X) ≡ if C(X) then D(X) 
 else begin 
 A(X); P(f(X)); 
 B(X); P(g(X)); 
 end; 
 Đệ quy với
 2 lần gọi đệ quy
▪ Thuật toán khử đệ quy tương ứng với thủ tục đệ quy
 P(X) ≡ { 
 Create_Stack (S) : 
 Push (S, (X,1)) ; 
 Repeat 
 While ( not C(X) ) do begin 
 A(X) ; 
 Push (S, (X,2)) ; 
 X := f(X) ; 
 end; 
 D(X) ; 
 POP (S, (X,k)) ; 
 if ( k 1) then begin 
 B(X) ; 
 X := g(X) ; 
 end; 
 until ( k = 1 ) ; 
 }
 Ví dụ
 Bài toán Tháp Hà Nội
Đệ quy Khử đệ quy
THN(n,X,Y,Z) ≡ if(n > 0) THN {
{ Create_Stack (S) ; 
 THN (n - 1, X, Z, Y); Push (S ,(n,X,Y,Z,1)) ; 
 Move (X, Z ); Repeat 
 THN (n - 1, Y, X, Z); While (n > 0) do begin 
} Push (S ,(n,X,Y,Z,2)) ; 
 n = n - 1; 
Trong đó Swap (Y,Z) ; 
▫Biến X là bộ (n,X,Y,Z) end ; 
▫C(X) là n<=0 Pop (S,(n,X,Y,Z,k)) ; 
▫D(X), A(X) là rỗng if ( k 1 ) then begin 
▫B(X) = B(n,X,Y,Z) là move(X, Z)
▫f(X) = f(n,X,Y,Z) = (n-1,X,Z,Y) Move (X ,Z ) ; 
▫g(X) = g(n,X,Y,Z) = (n-1,Y,X,Z) n = n - 1 ; 
 Swap (X,Y) ; 
 end ; 
 until ( k == 1 ) ; 
 }
 Cho dãy số
Ví dụ 1,2,3,7,14,27,55,110,219....
 Viết hàm đệ quy tính số hạng thứ n của dãy số
 (n > 2 nhập từ bàn phím), rồi tính tổng các số
 hạng của dãy
 Sau đó, khử đệ quy chương trình trên