Bài giảng Kiểm toán căn bản - Bài 4: Đối tượng và phương pháp của kiểm toán (Phần 2) - Đinh Thế Hùng
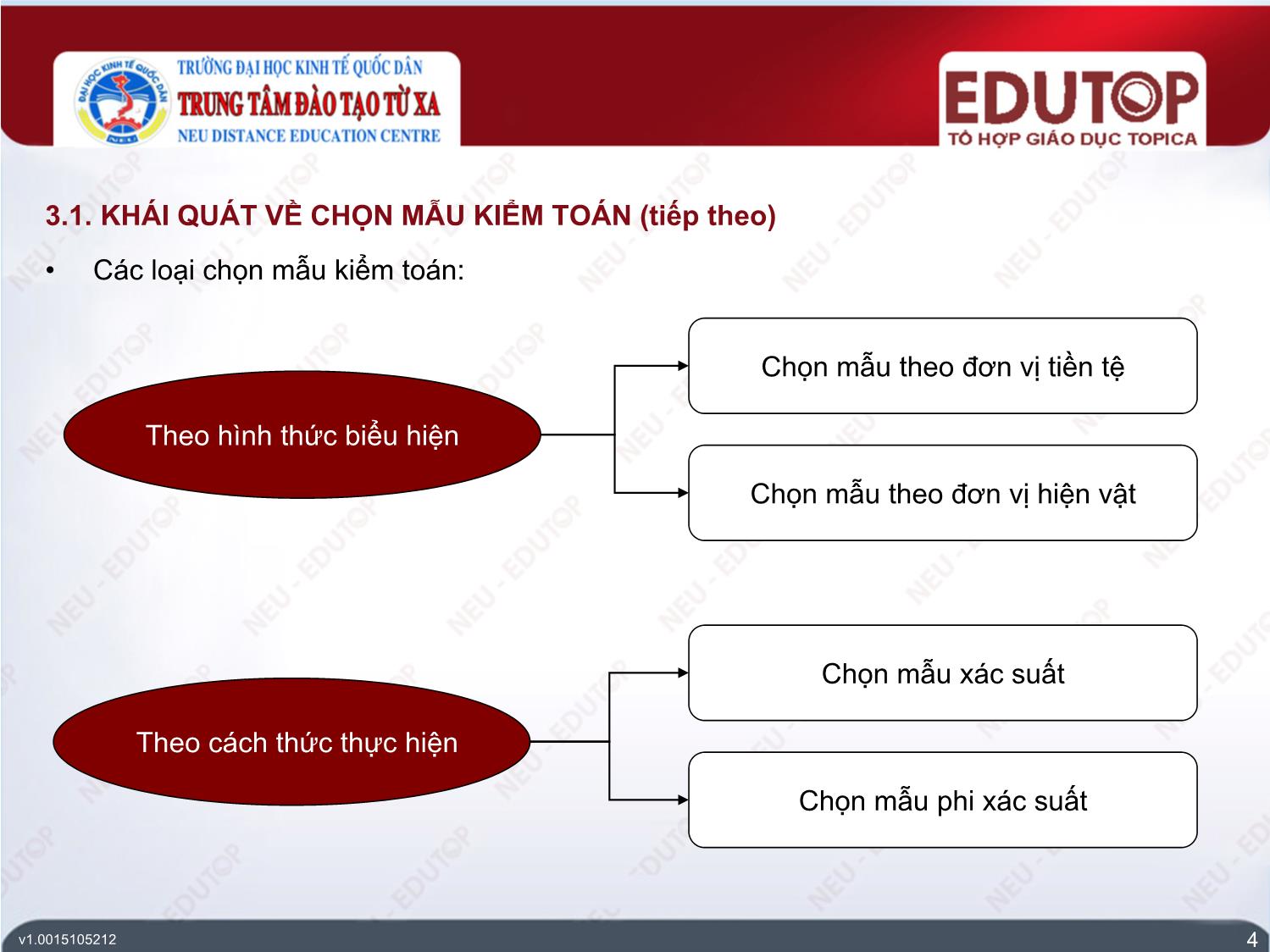
3.1. KHÁI QUÁT VỀ CHỌN MẪU KIỂM TOÁN
• Chọn mẫu kiểm toán là việc lựa chọn một số phần tử
(gọi là mẫu) từ một tập hợp các phần tử (gọi là tổng
thể) và dùng các đặc trưng của mẫu để rút ra các suy
đoán về đặc trưng của toàn bộ tổng thể.
• Yêu cầu cơ bản của chọn mẫu: Mẫu được chọn phải
là mẫu đại diện mang đầy đủ các đặc trưng của tổng
thể mà mẫu được chọn ra.
• Các loại rủi ro trong chọn mẫu kiểm toán:
Rủi ro do chọn mẫu là khả năng mà kết luận của kiểm toán viên dựa trên mẫu sai
lệch so với kết luận mà kiểm toán viên cũng sử dụng thử nghiệm tương tự áp dụng
đối với toàn bộ tổng thể.
Rủi ro không do chọn mẫu là khả năng kiểm toán viên đưa ra những kết luận sai lầm
không phải do lỗi chọn mẫu mà do các yếu tố không liên quan trực tiếp đến việc
chọn mẫu

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5

Trang 6

Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Kiểm toán căn bản - Bài 4: Đối tượng và phương pháp của kiểm toán (Phần 2) - Đinh Thế Hùng

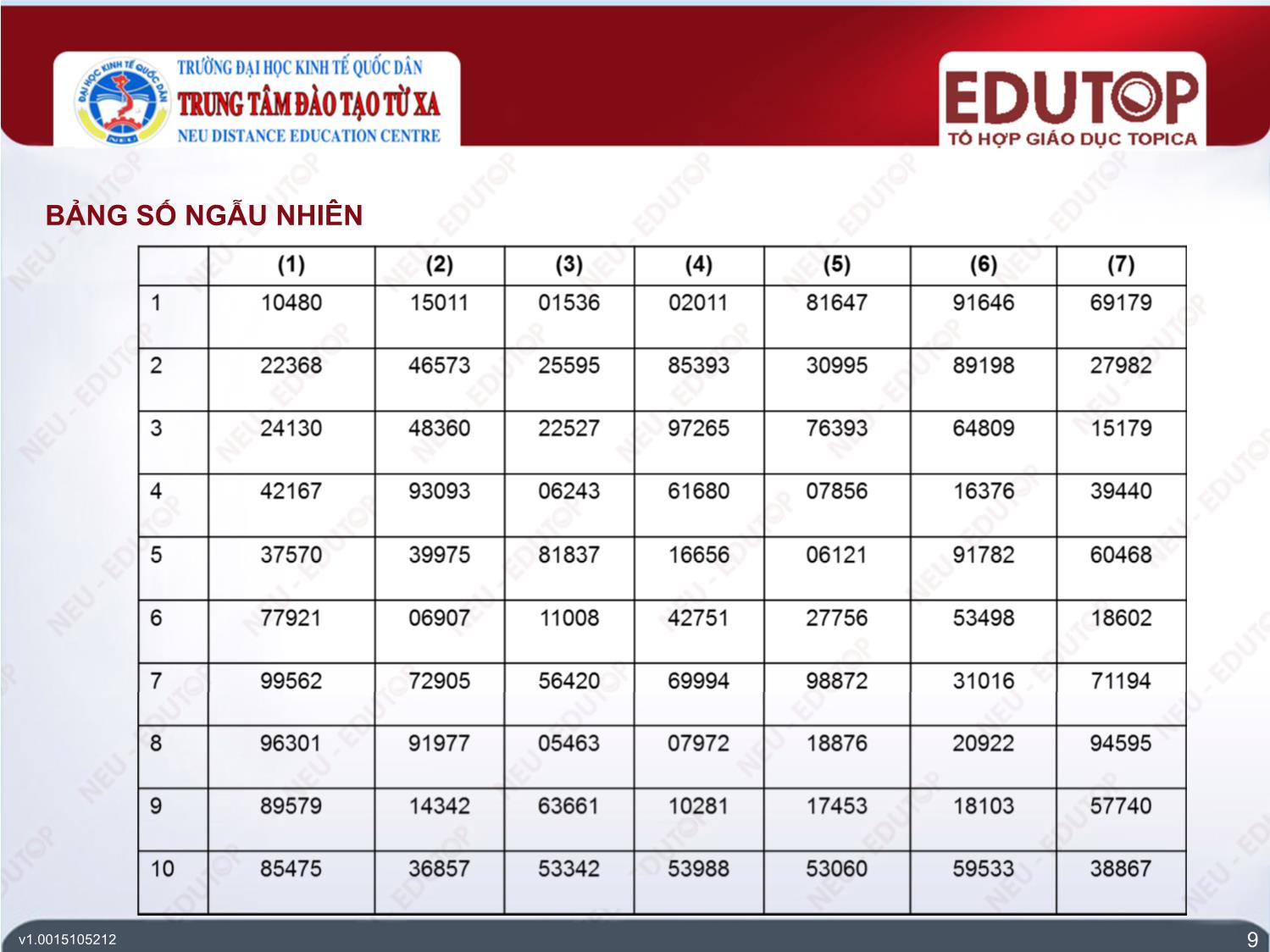
CHỌN MẪU XÁC SUẤT THEO ĐƠN VỊ HIỆN VẬT (tiếp theo) 8 Chọn mẫu theo bảng số ngẫu nhiên • Bước 3: Xác định lộ trình sử dụng bảng số ngẫu nhiên (Chọn theo 2 hướng). • Chọn theo chiều dọc: Chọn từ trên xuống dưới. Chọn từ dưới lên trên. • Chọn theo chiều ngang: Chọn từ phải qua trái Chọn từ trái qua phải. • Bước 4: Xác định điểm xuất phát: Điểm xuất phát phải được xác định ngẫu nhiên. v1.0015105212 BẢNG SỐ NGẪU NHIÊN 9 v1.0015105212 3.2.1. CHỌN MẪU XÁC SUẤT THEO ĐƠN VỊ HIỆN VẬT (tiếp theo) Ví dụ chọn mẫu theo bảng số ngẫu nhiên: Chọn 5 Phiếu chi từ tập hợp các Phiếu chi có số hiệu từ 2564 đến 6839 theo cách chọn mẫu sử dụng bảng số ngẫu nhiên, với điểm xuất phát là Dòng 1 Cột 3. Bài giải: • Bước 1: Định dạng các phần tử: (2564 – 6839). Do yêu cầu chỉ lựa chọn các Phiếu chi có số hiệu từ 2564 đến 6839 nên các Phiếu chi có số hiệu nhỏ hơn 2564 và Phiếu chi số hiệu lớn hơn 6839 sẽ bị loại, không được lựa chọn. • Bước 2: Xác định mối quan hệ: Quan hệ 4/5. Do số hiệu của các phiếu chi chỉ có 4 chữ số nhưng số ngẫu nhiên trên Bảng số ngẫu nhiên có 5 chữ số nên có 2 cách lựa chọn là chọn 4 chữ số đầu tiên hoặc 4 chữ số cuối của số ngẫu nhiên. Giả sử chọn 4 chữ số đầu của số ngẫu nhiên trên bảng số. 10 v1.0015105212 3.2.1. CHỌN MẪU XÁC SUẤT THEO ĐƠN VỊ HIỆN VẬT (tiếp theo) 11 Ví dụ chọn mẫu theo bảng số ngẫu nhiên: Chọn 5 Phiếu chi từ tập hợp các Phiếu chi có số hiệu từ 2564 đến 6839 theo cách chọn mẫu sử dụng bảng số ngẫu nhiên, với điểm xuất phát là Dòng 1 Cột 3. Bài giải: • Bước 3: Xác định lộ trình sử dụng Bảng số ngẫu nhiên: Cần phải chọn cách di chuyển theo cả 2 hướng của Bảng số là theo cột và theo hàng. Giả sử bài này lựa chọn theo hướng sau: Di chuyển theo cột: Đi theo chiều từ trên xuống dưới. Di chuyển theo hàng: Đi theo chiều từ trái qua phải. • Bước 4: Xác định điểm xuất phát: Theo đề bài cho điểm xuất phát là Dòng 1, cột - tại điểm đó có số ngẫu nhiên là: 01536. Theo quy định trong bước 2 là lấy 4 chữ số đầu của số ngẫu nhiên do đó số ngẫu nhiên bắt đầu được sử dụng để lựa chọn là: 0153. v1.0015105212 3.2.1. CHỌN MẪU XÁC SUẤT THEO ĐƠN VỊ HIỆN VẬT (tiếp theo) • Kết quả chọn mẫu theo bảng Số ngẫu nhiên (2564 – 6839) Số ngẫu nhiên đầu tiên được dùng để lựa chọn là 0153 không nằm trong khoảng từ (2564 – 6839) theo quy định tại bước 1 do đó bị Loại. Sau đó sẽ di chuyển xuống dòng 2, cột 3 sẽ lựa chọn được số 2559 và cũng không nằm trong khoảng từ (2564 – 6839) nên cũng bị Loại Tương tự như vậy đến dòng 7, cột 3 lựa chọn được số 5642 và số này nằm trong khoảng từ (2564 – 6839) nên được Chọn hay Phiếu chi số 5642 sẽ được rút ra để kiểm tra. Với cách chọn như trên, tại dòng 9, dòng 10, dòng 12 và dòng 13 của cột 3, sẽ chọn được các số 6366, 5334, 4823, 5263 cũng nằm trong khoảng từ (2564 – 6839) và các Phiếu chi có số hiệu tương ứng sẽ được lựa chọn rút ra để kiểm tra. 12 v1.0015105212 3.2.1. CHỌN MẪU XÁC SUẤT THEO ĐƠN VỊ HIỆN VẬT (tiếp theo) 13 Chọn mẫu theo hệ thống • Khái niệm: Chọn mẫu ngẫu nhiên theo hệ thống là quá trình chọn máy móc theo khoảng cách được xác định trên cơ sở kích cỡ của quần thể và số lượng mẫu cần chọn. • Các bước tiến hành lấy mẫu: Bước 1: Xác định quy mô tổng thể (N). Nếu là dãy số liên tục thì quy mô tổng thể được xác định như sau: N = (Phần tử cuối – Phần tử đầu) + 1 Bước 2: Xác định quy mô mẫu (M). M = Số lượng mẫu cần chọn Bước 3: Xác định khoảng cách cố định (K). K= N/M Bước 4: Xác định điểm xuất phát (M1). Mi = M(i –1) + K hoặc Mi = M1 + (i – 1) × K v1.0015105212 3.2.1. CHỌN MẪU XÁC SUẤT THEO ĐƠN VỊ HIỆN VẬT (tiếp theo) Ví dụ chọn mẫu theo khoảng cách: Chọn 5 Phiếu chi từ tập hợp các Phiếu chi có số hiệu từ 2564 đến 6839 theo cách chọn mẫu hệ thống, với điểm xuất phát là M1= 2800. Bài giải: • Bước 1: Xác định quy mô tổng thể Đây là một dãy liên tục các Phiếu chi do đó quy mô tổng thể được xác định như sau: N = (6839 – 2564) + 1= 4276 • Bước 2: Xác định kích cỡ mẫu: Theo yêu cầu đề bài cần phải chọn 5 Phiếu chi do đó M = 5. 14 v1.0015105212 3.2.1. CHỌN MẪU XÁC SUẤT THEO ĐƠN VỊ HIỆN VẬT (tiếp theo) 15 Ví dụ chọn mẫu theo khoảng cách: Chọn 5 Phiếu chi từ tập hợp các Phiếu chi có số hiệu từ 2564 đến 6839 theo cách chọn mẫu hệ thống, với điểm xuất phát là M1= 2800. Bài giải: • Bước 3: Xác định khoảng cách cố định. K = 4276/ 5 = 855,2 Tuy nhiên không có Phiếu chi số 855,2 do đó sẽ lựa chọn số nguyên là 855. • Bước 4: Xác định điểm xuất phát. M1= 2800 (đã cho trong đề bài) Phần tử thứ 2 được xác định theo công thức: M2 = M1 + (2 – 1) × K M2 = 2800 + (2 – 1) × 855 = 3655 Hoặc M2 = M1 + K M2 = 2800 + 855 = 3655 Tương tự: M3 = 2800 + (3 – 1) × 855 = 4510 = 3655 + 855 = 4510 M4 = 5365 M5 = 6220 v1.0015105212 3.2.2. CHỌN MẪU PHI XÁC SUẤT • Khái niệm: Chọn mẫu phi xác suất là cách chọn mẫu theo phán đoán chủ quan và không dựa theo phương pháp máy móc, khách quan. • Trong chọn mẫu phi xác suất gồm: Chọn mẫu theo khối. Chọn mẫu theo nhận định. 16 v1.0015105212 3.2.2. CHỌN MẪU PHI XÁC SUẤT (tiếp theo) Chọn mẫu theo khối • Khái niệm: Chọn mẫu theo khối là việc chọn một tập hợp các mẫu liên tục trong một dãy nhất định. • Nguyên tắc: Khi phần tử đầu tiên trong khối đã được chọn thì phần còn lại cũng được chọn tất yếu. • Ví dụ: Chọn 10 phiếu thu bắt đầu từ số 3472 – 3472 – 3481. 17 Chọn mẫu theo nhận định • Khái niệm: Chọn mẫu theo nhận định là việc chọn mẫu hoàn toàn dựa trên những xét đoán chủ quan của nhà nghề. • Trong nhiều trường hợp, khi có kích cỡ mẫu nhỏ hoặc có tính huống không bình thường... chọn mẫu theo nhận định sẽ tạo cơ hội tốt cho sự xuất hiện của những mẫu đại diện. • Điều kiện tiến hành: Kiểm toán viên phải nắm được đặc điểm cơ bản của khách thể kiểm toán và ấn định được mẫu đại diện trước khi chọn mẫu. v1.0015105212 3.3. KỸ THUẬT PHÂN TẦNG TRONG CHỌN MẪU KIỂM TOÁN • Khái niệm Phân tầng là kỹ thuật phân chia một tổng thể thành nhiều nhóm nhỏ hơn mà các đơn vị trong cùng một nhóm có đặc tính khá tương đồng với nhau. • Mục đích Việc phân tầng sẽ làm giảm sự khác biệt trong cùng một tầng và giúp kiểm toán viên tập trung vào những bộ phận chứa đựng nhiều khả năng sai phạm. • Bảng phân tầng các khoản phải thu: 18 Tầng Qui mô Cấu tạo của tầng Chọn mẫu 1 22 Các khoản phải thu có giá trị > 5.000 USD Kiểm tra 100% 2 121 Tất cả các khoản có giá trị từ 1.000 đến 5.000 USD Dựa trên BSNN 3 85 Tât cả các khoản có giá trị < 1.000 USD Chọn hệ thống 4 14 Các khoản có số dư có Kiểm tra 100% v1.0015105212 3.4. CHỌN MẪU THEO ĐƠN VỊ TIỀN TỆ 3.4.2. Chọn mẫu ngẫu nhiên theo đơn vị tiền tệ sử dụng bảng số ngẫu nhiên 3.4.1. Đặc trưng 3.4.3. Chọn mẫu ngẫu nhiên theo đơn vị tiền tệ theo phương pháp hệ thống 3.4.4. Ví dụ 19 v1.0015105212 3.4.1. ĐẶC TRƯNG • Đơn vị mẫu được chuyển hoá từ đơn vị hiện vật sang đơn vị tiền tệ. • Mỗi đơn vị tiền tệ trở thành một phần tử của tập hợp. • Chọn mẫu theo đơn vị tiền tệ cũng sử dụng các kỹ thuật chọn mẫu phổ biến. • Tổng thể sẽ là số tiền luỹ kế của đối tượng kiểm toán. • Trọng tâm kiểm toán thường rơi vào các đơn vị có giá trị lớn. • Kích cỡ mẫu thường lớn hơn so với đơn vị hiện vật. 20 v1.0015105212 3.4.2. CHỌN MẪU NGẪU NHIÊN THEO ĐƠN VỊ TIỀN TỆ SỬ DỤNG BẢNG SỐ NGẪU NHIÊN (tiếp theo) Các bước tiến hành • Bước 1: Xác định số luỹ kế. Trong bước này, tiến hành cộng dồn số tiền của các phần tử và mỗi phần tử trong tổng thể sẽ tương ứng với một số cộng dồn. • Bước 2: Định dạng các phần tử. Việc định dạng này là nhằm xác định khoảng số liệu được dùng để lựa chọn số ngẫy nhiên trên Bảng số ngẫu nhiên. Khoảng số này thường từ 0 đến số lũy kế cuối cùng. • Bước 3: Xác định mối quan hệ giữa số lũy kế với số ngẫu nhiên trên bảng số ngẫu nhiên. Việc xác định mối quan hệ này tương tự như trong cách chọn mẫu theo đơn vị hiện vật ở mục Chọn mẫu theo khối. 21 v1.0015105212 3.4.2. CHỌN MẪU NGẪU NHIÊN THEO ĐƠN VỊ TIỀN TỆ SỬ DỤNG BẢNG SỐ NGẪU NHIÊN (tiếp theo) 22 Các bước tiến hành: • Bước 4: Xác định lộ trình sử dụng Bảng số ngẫu nhiên. Việc xác định này được thực hiện tương tự như bước 3 trong cách chọn mẫu theo đơn vị hiện vật ở mục Chọn mẫu theo khối. • Bước 5: Xác định điểm xuất phát và tìm số ngẫu nhiên. Việc xác định này được thực hiện tương tự như bước 4 trong cách chọn mẫu theo đơn vị hiện vật ở mục Chọn mẫu theo khối. • Bước 6: Xác định số lũy kế từ số ngẫu nhiên đã chọn. Do số ngẫu nhiên thường nằm giữa 2 số lũy kế vì vậy để lựa chọn số lũy kế có 2 cách sau: Chọn các số lũy kế có giá trị lớn hơn số ngẫu nhiên đã lựa chọn. Chọn các số lũy kế có giá trị gần với số ngẫu nhiên hơn. • Bước 7: Xác định các số dư từ số lũy kế đã chọn. Sau khi đã xác định được số lũy kế thì xác định được phần tử (số dư) cần lựa chọn do tương ứng với mỗi số dư là một số lũy kế. v1.0015105212 3.4.2. CHỌN MẪU NGẪU NHIÊN THEO ĐƠN VỊ TIỀN TỆ SỬ DỤNG BẢNG SỐ NGẪU NHIÊN (tiếp theo) Bảng trình bày kết quả chọn mẫu: 23 Số ngẫu nhiên Số lũy kế Số dư STT v1.0015105212 3.4.3. CHỌN MẪU NGẪU NHIÊN THEO ĐƠN VỊ TIỀN TỆ THEO PHƯƠNG PHÁP HỆ THỐNG Các bước tiến hành • Bước 1: Xác định số luỹ kế. Tiến hành cộng dồn các số dư và tương ứng mỗi số dư sẽ có một số lũy kế. • Bước 2: Xác định quy mô tổng thể (N). N = Số lũy kế cuối cùng • Bước 3: Xác định quy mô mẫu (M). M = Số lượng mẫu cần chọn từ tổng thể • Bước 4: Xác định khoảng cách cố định (K). K= N/M 24 v1.0015105212 3.4.3. CHỌN MẪU NGẪU NHIÊN THEO ĐƠN VỊ TIỀN TỆ THEO PHƯƠNG PHÁP HỆ THỐNG 25 Các bước tiến hành • Bước 5: Xác định điểm xuất phát và các số ngẫu nhiên. Điểm xuất phát được xác định từ đầu và phải đảm bảo ngẫu nhiên. Xác định các số ngẫu nhiên tiếp theo theo công thức sau: Mi = Mi – 1 + K hoặc Mi = M1 + (i – 1) × K • Bước 6: Xác định số luỹ kế từ số ngẫu nhiên đã được chọn. Thực hiện như Bước 6 ở mục 3.4.2. • Bước 7: Xác định các số dư từ số luỹ kế đã chọn. Thực hiện như Bước 7 ở mục 3.4.2. v1.0015105212 3.4.4. VÍ DỤ Chọn 5 khoản phải trả trong tập hợp các khoản phải trả của công ty A cho dưới đây để tiến hành gửi thư xác nhận. • Áp dụng phương pháp chọn mẫu sử dụng Bảng số ngẫu nhiên với điểm xuất phát là Dòng 10, Cột 2 và tiến hành chọn mẫu không lặp lại. • Áp dụng phương pháp chọn mẫu theo hệ thống với điểm xuất phát là M1 = 1200. 26 v1.0015105212 3.4.4. VÍ DỤ 27 Danh sách các khoản phải trả: v1.0015105212 3.4.4. VÍ DỤ (tiếp theo) • Bước 1: Cộng dồn số liệu. 28 v1.0015105212 3.4.4. VÍ DỤ (tiếp theo) 29 • Bước 2: Định dạng các phần tử. Khoảng lựa chọn là (0 – 8294). Theo bảng số liệu cộng dồn ở bước 1, ta sẽ lựa chọn các số ngẫu nhiên nằm trong khoảng từ 0 đến số lũy kế cuối cùng là: 8294. • Bước 3: Xác định mối quan hệ giữa số lũy kế với số ngẫu nhiên trên bảng số ngẫu nhiên. Do số lũy kế trong trường hợp này có 4 chữ số nên có 2 cách chọn (xem mục 3.2.1). Giả sử, lấy 4 chữ số cuối của số ngẫu nhiên. • Bước 4: Xác định lộ trình sử dụng Bảng số ngẫu nhiên Lộ trình được xác định theo 2 hướng sau: Theo hàng: Đi từ trên xuống dưới (từ dòng 1 xuống dòng 45). Theo dòng: Đi từ trái qua phải (từ cột 1 sang cột 7). v1.0015105212 3.4.4. VÍ DỤ (tiếp theo) • Bước 5: Xác định điểm xuất phát và tìm số ngẫu nhiên. Theo đầu bài, điểm xuất phát là dòng 10, cột 2 của Bảng số ngẫu nhiên. Tại điểm này ta có số ngẫu nhiên là: 36857. Theo quy định tại bước 3 thì số ngẫu nhiên bắt đầu được lựa chọn là: 6857 và nằm trong khoảng được lựa chọn đã được quy định tại bước, nên số 6857 sẽ được lựa chọn. Tương tự như vậy sau khi di chuyển tiếp từ dòng 10 xuống các dòng tiếp theo, chúng ta sẽ chọn được các số ngẫu nhiên sau: 0961 (dòng 12, cột 2), 3969 (dòng 13, cột 2), 1129 (dòng 14, cột 2), 7336 (dòng 15, cột 2). Số ngẫu nhiên ở dòng 11, cột 2 là 9578 không nằm trong khoảng được lựa chọn nên bị loại. Giả sử trong trường hợp này chúng ta quy định là chọn mẫu không lặp lại. 30 v1.0015105212 3.4.4. VÍ DỤ (tiếp theo) 31 • Bước 6: Xác định số luỹ kế từ số ngẫu nhiên đã chọn Do số ngẫu nhiên thường nằm giữa 2 số lũy kế và có 2 cách lựa chọn đã nêu. Giả sử, trong bài này để lựa chọn số lũy kế chúng ta lựa cách sau: Chọn các số lũy kế có giá trị lớn hơn số ngẫu nhiên đã lựa chọn. Theo cách này ta sẽ lựa chọn như sau: Số ngẫu nhiên 6857 nằm giữa 2 số lũy kế là 6564 và 6897, do đó khi tuân theo quy định là lấy số lũy kế lớn hơn thì số lũy kế được lựa chọn là 6897. Tương tự, chúng ta chọn được các số lũy kế thể hiện trong bảng kết quả bên dưới. • Bước 7: Xác định các số dư từ số lũy kế đã chọn. Sau khi đã xác định được số lũy kế thì xác định được phần tử (số dư) cần lựa chọn do tương ứng với mỗi số dư là một số lũy kế, chúng ta đối chiếu ngang sang từ số lũy kế sẽ có số dư và số thứ tự tương ứng. v1.0015105212 3.4.4. VÍ DỤ (tiếp theo) • Kết quả chọn mẫu theo bảng số (0001 – 8294): 32 Số ngẫu nhiên Số lũy kế Số dư STT 6857 0961 3969 1129 7336 2765 6897 1264 4576 Không chọn 7368 2797 333 389 628 - 471 100 16 2 12 - 17 5 v1.0015105212 3.4.4. VÍ DỤ (tiếp theo) 33 Số ngẫu nhiên Số lũy kế Số dư STT 6857 0961 3969 1129 7336 2765 6897 1264 4576 Không chọn 7368 2797 333 389 628 - 471 100 16 2 12 - 17 5 v1.0015105212 3.4.4. VÍ DỤ (tiếp theo) Chú ý • Trong các số ngẫu nhiên đã lựa chọn có 2 số là: 0961 và 1129 đều lựa chọn số lũy kế là 1264 do đó vi phạm quy định tại bước 5 là chọn mẫu không lặp lại. Vì vậy, chúng ta phải loại số ngẫu nhiên 1129 và chọn bổ sung số ngẫu nhiên 2765 tại dòng 16, cột 2 và được kết quả như trong bảng. • Trong trường hợp, tại bước 5 quy định chọn mẫu lặp lại thì số ngẫu nhiên 1129 cũng sẽ được lựa chọn và như vậy số lũy kế 1264 sẽ được xuất hiện 2 lần trong mẫu được lựa chọn. 34 v1.0015105212 3.4.4. VÍ DỤ (tiếp theo) 35 • Kết quả chọn mẫu theo hệ thống (0001 – 8294): Số ngẫu nhiên Số lũy kế Số dư STT M1 = 1200 M2 = 2858 M3 = 4516 M4 = 6174 M5 = 7832 1264 2918 4576 6564 7930 389 82 628 1368 562 2 7 12 15 18 v1.0015105212 3.4.4. VÍ DỤ (tiếp theo) 36 Số ngẫu nhiên Số lũy kế Số dư STT M1 = 1200 M2 = 2858 M3 = 4516 M4 = 6174 M5 = 7832 1264 2918 4576 6564 7930 389 82 628 1368 562 2 7 12 15 18 v1.0015105212 TÓM LƯỢC CUỐI BÀI Mục 3, người học cần nắm rõ các khái niệm cơ bản trong chọn mẫu kiểm toán và tìm hiểu các phương pháp chọn mẫu được ứng dụng cho thử nghiệm kiểm soát và thử nghiệm cơ bản. Các phương pháp chọn mẫu bao gồm: chọn mẫu xác suất và chọn mẫu phi xác suất. Trong mỗi phương pháp chọn lại có nhiều cách chọn khác nhau như đối với chọn mẫu xác suất có ba cách chọn: chọn mẫu dựa trên bảng số ngẫu nhiên, chọn dựa theo chương trình vi tính và chọn mẫu hệ thống. Còn đối với chọn mẫu phi xác suất có các cách chọn như chọn mẫu theo khối và chọn mẫu theo nhận định nhà nghề. Để bổ trợ cho công tác chọn mẫu có hiệu quả, phần này còn đề cập tới kĩ thuật phân tầng, phân tổ. Bên cạnh đó cần nắm vững cách chọn mẫu theo đơn vị tiền tệ với các đặc điểm riêng và trình tự chọn mẫu được áp dụng. 37
File đính kèm:
 bai_giang_kiem_toan_can_ban_bai_4_doi_tuong_va_phuong_phap_c.pdf
bai_giang_kiem_toan_can_ban_bai_4_doi_tuong_va_phuong_phap_c.pdf

