Bài giảng Introduction to Computer Programming (C language) - Chapter 6: Functions - Võ Thị Ngọc Châu

he C Programming Language”, 2nd Ed. 
 – Brian W. Kernighan and Dennis M. Ritchie, 
 Prentice Hall, 1988 
 and others, especially those on the Internet 
 3 
Content 
 Introduction 
 Functions in the standard library 
 An example of a function 
 Components of a function 
 Function call 
 Recursion 
 Summary 
 4 
 Introduction 
 In the previous chapters, we have used 
 several so-called functions in the library: 
  printf in stdio.h 
 Those functions are modular 
  scanf in stdio.h 
 processing units that are: 
  fflush in stdio.h 
 Responsible for a 
  sqrt in math.h 
 certain task 
  pow in math.h 
  system in stdlib.h Reusable in many 
  strcmp in string.h various programs 
  strcpy in string.h 
 5 
 Functions in the standard library 
Source: www.tutorialspoint.com 6 
 Functions in the standard library 
 Some functions in 
  int printf(const char *format, ...) 
 Sends formatted output to stdout 
  int scanf(const char *format, ...) 
 Reads formatted input from stdin 
  int getchar(void) 
 Gets a character (an unsigned char) from stdin 
  char *gets(char *str) 
 Reads a line from stdin and stores it into the string pointed 
 to, by str. It stops when either the newline character („\n‟) 
 is read or when the end-of-file (EOF) is reached, whichever 
 comes first. 7 
 Functions in the standard library 
 Some functions in 
  double cos(double x) 
 Returns the cosine of a radian angle x 
  double pow(double x, double y) 
 Returns x raised to the power of y 
  double sqrt(double x) 
 Returns the square root of x 
  double ceil(double x) 
 Returns the smallest integer value greater than or equal 
 to x 
  double floor(double x) 
 Returns the largest integer value less than or equal to x 8 
 Functions in the standard library 
 Some functions in 
  void *malloc(size_t size) 
 Allocates the requested memory and returns a pointer to it 
  void free(void *ptr) 
 Deallocates the memory previously allocated by a call to 
 calloc, malloc, or realloc 
  int rand(void) 
 Returns a pseudo-random number in the range of 0 to 
 RAND_MAX (at least 32767, up to implementation) 
  int system(const char *string) 
 The command specified by string is passed to the host 
 environment to be executed by the command processor 
 . E.g. “pause”, “cls”, “date” 9 
 Introduction 
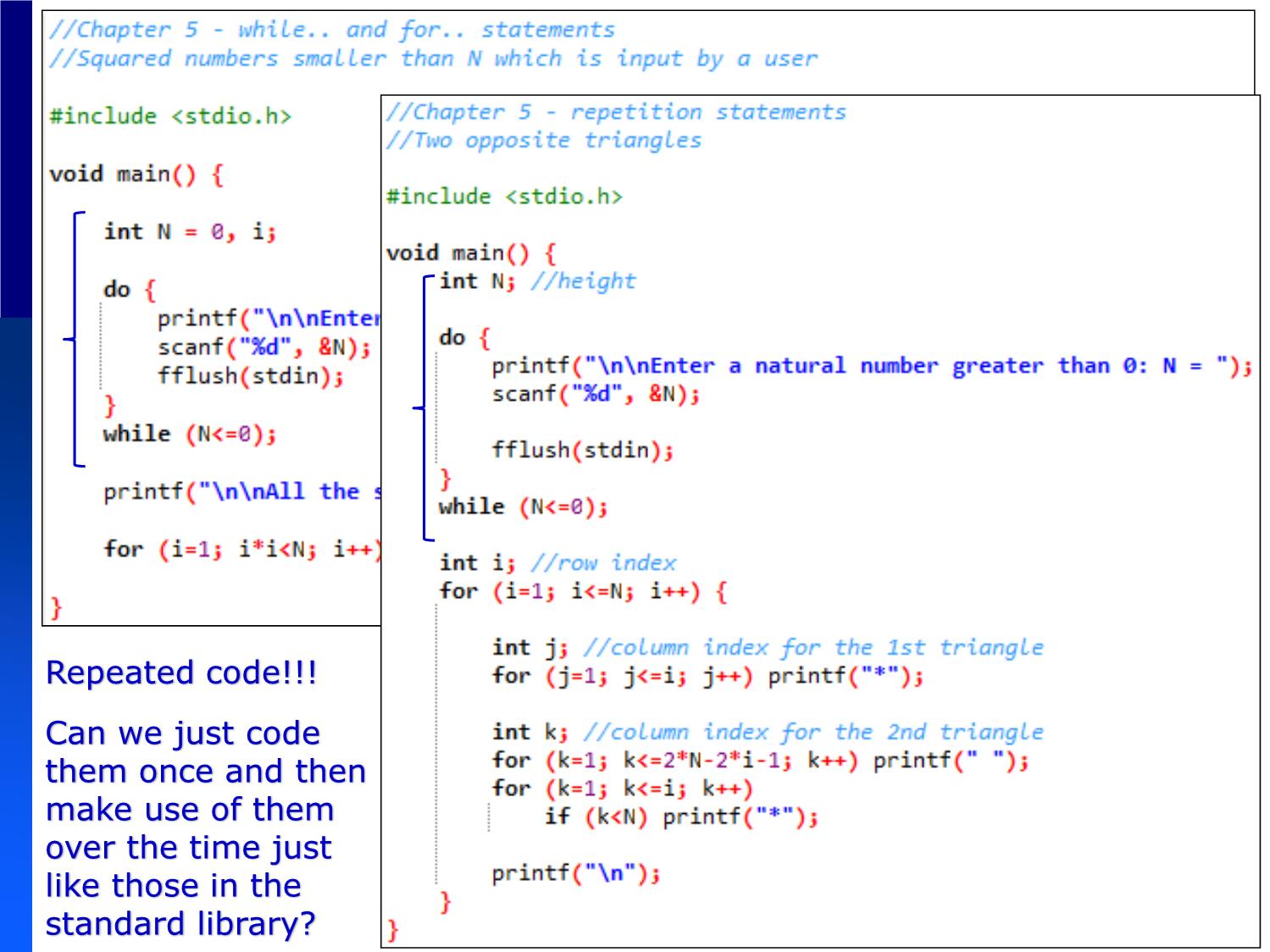
Repeated code!!! 
Can we just code 
them once and then 
make use of them 
over the time just 
like those in the 
standard library? 10 
Introductions 
 Let‟s define a function: getNaturalNumber() 
 Declared in a header file 
 C6_function_getNaturalNumber_1.h 
 for multiple uses 
 Source code file: C6_function_getNaturalNumber.c 
 Purpose: to ask users to input a natural number 
 until a valid number is input 11 
Use of our previously defined 
function, which is declared in 
a header file: 
“C6_function_getNaturalNumber_1.h” 
 Compile: 
 gcc C6_starTriangle_function_1.c C6_function_getNaturalNumber.c 
 –o C6_starTriangle_function_1.exe 12 
Introduction 
 A function 
  A processing unit to perform a specific task 
  A means to modularize a program for 
 manageable program development 
 C Program 1 C Program 2 
 main() main() 
 Divide-and-conquer 
 function1() function1() Reusable 
 Information hiding 
 function2() function3() 
 Abstraction 
   Easy for debugging 
 13 
Introduction 
 Issues related to functions 
  Function definition 
  Function declaration 
  Function call 
 14 
 An example of a function 
 Prepare your own library for numbers 
  Compute the sum of N first natural numbers 
 sum = 1 + 2 + 3 +  + (N-1) + N 
  Compute the factorial of N, a natural number 
 factorial = 1*2*3**(N-1)*N 
  Compute the n-th power of x, a floating-point 
 number 
 xn = x*x*x**x 
  Count the number of digits in N, a natural number 
 N = 123456 => Number of digits = 6 
  Round x, a floating-point number, with two digits 
 after the decimal point 
 x = 1.23456 => x = 1.23 
 x = 9.87654321 => x = 9.88 15 
 An example of a function 
 Prepare your own library for numbers 
  Check if a natural number is a prime number 
 7 => true ( 0) 
 8 => false (0) 
  Check if a natural number is a squared number 
 4 => true ( 0) 
 8 => false (0) 
  Toggle non-zero digits to „9‟ digits in an integer number to 
 generate its 9-based mask 
 113789 => 999999 
 -10789 => -90999 
  Count the number of occurrences of each digit in an integer 
 number 
 113789 => 0: 0; 1: 2; 2: 0; 3: 1; 4: 0; 5: 0; 6: 0; 7: 1; 8: 1; 9: 1 
 -20054 => 0: 2; 1: 1; 2: 1; 3: 0; 4: 1; 5: 1; 6: 0; 7: 0; 8: 0; 9: 0 
An example of a function 
 Prepare your own library for numbers 
  Estimate a value of e, the natural number 
  Estimate a value of ex 
  Estimate a value of PI 
   17 
Components of a function 
 Given N, a natural number, calculate the 
 factorial of N: N! = 1*2*..*N = (N-1)!*N 
 18 
 Components of a function 
 Given N, a natural number, calculate the 
 factorial of N: N! = 1*2*..*N = (N-1)!*N 
 Parameter list Function 
Return with comma body that 
type separation. includes 
 Function 
which is No default declarations 
 name 
a data value for each and 
type of parameter in C statements 
the value functions. performed 
returned for a 
 return statement to return a specific task 
 value of a return type to the caller 
 19 
 Components of a function 
 [static] return-type function-name (argument-declarations) 
 { 
 declarations and statements 
 } 
 - function-name: a valid identifier 
 - argument-declarations: a list of formal parameters in communication 
Part + Each parameter is regarded as a local variable with a data type. 
of the + Each parameter can be specified with “const” for unchanged intention. 
input 
 + Each parameter can be passed by value or by reference if it is a pointer. 
Process - declarations: a list of local variables 
ing in + Each variable can be auto or static with one single initialization. 
its 
body - statements: zero, one, or many statements of any kind 
 - return-type: a valid data type or void 
Part + Statement return []; in the body is used to end the 
of the 
output called function and return [a value] to its caller. If not, close brace of the 
 body ends the called function and program control is switched to its caller. 
 - [static]: optional specification to make the function available only in the file 
Charac
teristic where it is defined. 20 
Concepts related to functions 
 Function definition: 
 [static] return-type function-name (argument-declarations) 
 { 
 declarations and statements 
 } 
 Function prototype: 
 return-type function-name (argument-declarations); 
 Function signature: 
 [extern] return-type function-name (argument-declarations) 
 No concept of “nested functions”! 
  Implementation-dependent 21 
 Where is a function defined and 
 declared? 
 A function definition can be placed in: 
  the same file where the main() function is 
 Before the main() function 
 After the main() function 
  a separated file where the main() function is not 
 Regardless of where a function is defined, its 
 declaration is required before any call to it. 
  Function prototype in the global declaration section 
  Function prototype in a header file for common use 
 22 
 A program for an approximation 
 of the x-th power of e 
 Function definition 
 = Function declaration 
 (as it is placed before its call) 
Function declaration 
 a call to a function 
 Function definition 
 (a function declaration is required 
 as it is placed after its call.) 
 23 
Where is a function defined and 
declared? 
 SEPARATED FILES 
 Function declaration 
 Function 
 definition 
 Function calls 
 24 
Where is a function defined and 
declared? 
 Source file 
 getFactorial.c 
 25 
Where is a function defined and 
declared? 
 Source file 
 getPower.c 
 26 
Where is a function defined and 
declared? 
 Header file for common use 
 mynumber.h 
 27 
 Function call 
 Function call is a mention of a function to 
 another function or itself. 
  The function whose function body contains a a 
 mention is called a calling function or a caller. 
  The function whose name is mentioned in the caller‟s 
 function body is called a called function or a callee. 
  The caller is the same as or different from the callee. 
 The program in C6_function_myNumber 
  The main() function calls the printf(), scanf(), pow(), 
 factorial(), and power() functions. 
 Caller = main 
 Callees = printf, scanf, pow, factorial, power 
 28 
 Function call 
 A function call is mentioned in the function 
 body of the caller as: 
 function-name (argument-list) 
  argument-list 
 Optional, i.e. empty if the callee has no argument 
 Each argument is called actual parameter which is an 
 expression corresponding to a formal parameter by order. 
 Each argument has a type compatible with the type of its 
 corresponding formal parameter. Otherwise, type 
 conversion with promotion or truncation is performed. 
 Assignment of each expression value to the 
 corresponding formal parameter‟s memory is performed. 
  A value of a return type (if it is not void) is 
 returned via this function call. 29 
 Stack‟s values when i=0 in the 
 Function call main() function 
 Caller‟s stack Callee‟s stack 
 0 i 2 x 
 10 n 0 n 
 2 x i 
 0 e_x aPower 
The caller 
 The callee 30 
 Function call 
 Function call by value 
  Parameters are passed by value. 
 The actual parameter values are copied into local storage 
 of the formal parameters of the callee. 
  The caller and callee do not share any memory. 
 Function call by reference 
  C has no explicit reference parameters but 
 implements them via pointers, i.e. address passing. 
  Pointers are passed to the arguments. 
 There is only one copy of the value at any time. 
  The caller and callee have access to the value in 
 their shared memory through pointers. 
 31 
Function call 
 A function to swap two integer numbers 
 void swap(int a, int b){ 
 int temp; 
 a and b will be passed by 
 temp = a; values of int type. 
 a = b; 
 b = temp; 
 } 
 void swap(int *a, int *b){ 
 int temp; 
 temp = *a; a and b will be passed by pointers 
 *a = *b; to int values, i.e. addresses of the 
 memory that contains int values. 
 *b = temp; 
 } 
 32 
Function call by value 
 Change on formal parameters in the callee has 
 no impact on actual parameters in the caller. 33 
Function call by value 
 Stack‟s values when a=10 and 
 b=9 in the main() function 
 Caller‟s stack Callee‟s stack 
 10 a 10 a 
 9 b 9 b 
 temp 
 Stack‟s values 
 before the callee 
 ends 
 Callee‟s stack 
 9 a 
 10 b 
 10 temp 
 34 
 Function call by reference 
 Change on the shared memory can be made by both 
 callee and caller. Pointers are used for reference. 35 
Function call by reference 
 Stack‟s values when a=10 and 
 b=9 in the main() function 
 Caller‟s stack Callee‟s stack 
 000000000022FE4C 
 10 a &a 000000000022FE4C a 
 000000000022FE48 &b 
 9 b 000000000022FE48 b 
 temp 
 Stack‟s values 
 before the callee 
 ends 
 Caller‟s stack Callee‟s stack 
 000000000022FE4C 
 9 a &a 000000000022FE4C a 
 000000000022FE48 &b 
 10 b 000000000022FE48 b 
 10 temp 
 36 
 Recursion 
 A recursive function is a function that calls 
 itself either directly or indirectly. 
 When a function calls itself recursively, each 
 invocation gets a fresh set of all the automatic 
 variables, independent of the previous set. 
 Function to compute the factorial of n: 
 non-recursive vs. recursive versions 37 
rFactorial(10) rFactorial(10) 3628800 
 Recursion path 10*rFactorial(9) 10*9* 8*7*6*5*4*3*2*1*1 
 9*rFactorial(8) 9* 8*7*6*5*4*3*2*1*1 
 8*rFactorial(7) 8*7*6*5*4*3*2*1*1 
 7*rFactorial(6) 7*6*5*4*3*2*1*1 
 6*rFactorial(5) 6*5*4*3*2*1*1 
 5*rFactorial(4) 5*4*3*2*1*1 
 4*rFactorial(3) 4*3*2*1*1 
 3*rFactorial(2) 3*2*1*1 
 2*rFactorial(1) 2*1*1 
 Recursive cases 
 with smaller sizes 1*rFactorial(0) 1*1 
 Return path 
 1 1 
 Base case 38 
Recursion 
 Writing a recursive function 
  Determine and write the base cases and their 
 solutions 
 No recursive call is specified for those base cases. 
  Determine and write the recursive (inductive) 
 cases and their solutions 
 Establish a connection between the larger problem and 
 the smaller problems using recursive calls 
  Determine the other cases that are neither base 
 nor recursive cases 
 Check for other constraints with no recursive call 
 39 
 Recursion 
 Compute the sum of N first natural numbers 
  sum = 1 + 2 + 3 +  + (N-1) + N 
 Base case: sum(1) = 1 
 Recursive case: sum(N) = sum(N-1) + N 
 Compute the factorial of N, a natural number 
  factorial = 1*2*3**(N-1)*N 
 Base case: factorial(0) = factorial(1) = 1 
 Recursive case: factorial(N) = factorial(N-1)*N 
 Compute the n-th power of x, a floating-point 
 number 
  xn = x*x*x**x 
 Base case: power(x, 0) = 1 
 Recursive case: power(x, n) = power(x, n-1)*x 40 
Recursion 
 Estimate a value of e, the natural number 
  Base case: e(0) = 1 
  Recursive case: e(n) = e(n-1) + 1/factorial(n) 
 41 
Recursion 
 Estimate a value of ex 
  Base case: e_x(0) = 1 
  Recursive case: 
 e_x(n) = e_x(n-1) + power(x, n)/factorial(n) 
 42 
Recursion 
 Estimate a value of PI 
  Base case: pi(0) = 4 
  Recursive case: 
 pi(k) = pi(k-1) + power(-1, k)*4/(2*k+1) 
 43 
 Recursion 
 Hanoi Tower 
Move disks from peg 1 to 
peg 3 using peg 2 as a 
temporary holding area in 
such a way that smaller 
disks are always on top of 
larger disks and one disk peg 1 peg 2 peg 3 
is moved at a time 
 A recursive function with 4 parameters: 
 a). The number of disks to be moved 
 b). The peg on which these disks are initially threaded 
 c). The peg to which this stack of disks to be moved 
 d). The peg to be used as a temporary holding area 44 
Recursion 
 Hanoi Tower 
 45 
 Hanoi Tower 
peg 1 peg 2 peg 3 
 46 
 Recursion 
 Recursive function‟s concern 
  No saving in storage 
  Not faster 
  Infinite recursion 
 No base case is defined or base case can not be reached. 
 Recursive function‟s advantages 
  Compact recursive code 
  Easy to write and understand 
  Convenient for recursively defined data structures 
 and problems 
 47 
Summary 
 A function is a processing unit for a specific 
 task. 
  Divide-and-conquer approach 
  Reusability 
  Information hiding 
  Abstraction 
  Support for debugging 
 Manageable program development 
 48 
Summary 
 Function definition 
 Function declaration 
 Function call 
  By value 
  By reference with pointer implementation 
 Recursion 
  Recursive problem 
  Recursive data structure 
 49 
Chapter 6: Functions 
 50