Bài giảng Chương trình dịch - Chương 3: Phân tích cú pháp
Vai trò của bộ phân tích cú pháp
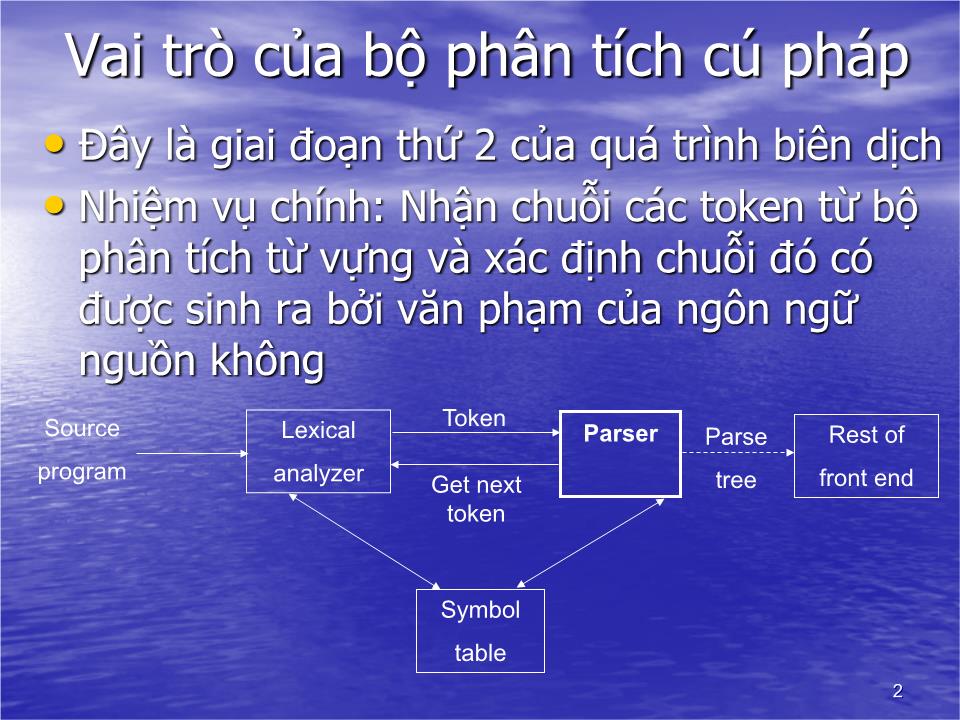
Đây là giai đoạn thứ 2 của quá trình biên dịch
Nhiệm vụ chính: Nhận chuỗi các token từ bộ phân tích từ vựng và xác định chuỗi đó có được sinh ra bởi văn phạm của ngôn ngữ nguồn không
Các phương pháp phân tích cú pháp (PTCP) chia làm hai loại: Phân tích từ trên xuống (top- down parsing) và phân tích từ dưới lên (bottom- up parsing)
Trong quá trình biên dịch xuất hiện nhiều lỗi trong giai đoạn PTCP do đó bộ phân tích cú pháp phải phát hiện và thông báo lỗi chính xác cho người lập trình đồng thơi không làm chậm những chương trình được viết đúng
Văn phạm phi ngữ cảnh
Để định nghĩa cấu trúc của ngôn ngữ lập trình ta dùng văn phạm phi ngữ cảnh (Context-free grammars) hay gọi tắt là một văn phạm
Một văn phạm bao gồm:
Các kí hiệu kết thúc (terminals): Chính là các token
Các kí hiệu chưa kết thúc (nonterminals): Là các biến kí hiệu tập các xâu kí tự
Các luật sinh (productions): Xác định cách thức hình thành các xâu từ các kí hiệu kết thúc và chưa kết thúc
Một kí tự bắt đầu (start symbol)

Trang 1
Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Chương trình dịch - Chương 3: Phân tích cú pháp

LLOW(T') = { +, ), $ }
FOLLOW(F) = { * ,+, ), $ }
27
Thuật giải xây dựng Parsing table M của văn phạm G:
1. Với mỗi luật sinh A của văn phạm, thực hiện bước 2 và 3
2. Với mỗi ký hiệu kết thúc a FIRST( ), thêm A vào M[A,a]
3. Nếu FIRST( ) thì đưa luật sinh A vào M[A,b] với mỗi ký hiệu kết thúc b FOLLOW(A). Nếu FIRST( ) và $ FOLLOW(A) thì đưa luật sinh A vào M[A,$].
4. Ô còn trống trong bảng tương ứng với lỗi (error).
28
Phân tích cú pháp từ dưới lên
Giới thiệu một kiểu phân tích cú pháp từ dưới lên tổng quát gọi là phân tích cú pháp Shift –Reduce
Một phương pháp tổng quát hơn của kỹ thuật Shift - Reduce là phân tích cú pháp LR (LR parsing) sẽ được thảo luận
Shift –Reduce parsing sẽ cố gắng xây dựng một parse tree cho một xâu nhập vào từ nút lá lên nút gốc. Nói cách khác ta "reducing" từng bước xâu nhập vào đến khi thu được kí hiệu bắt đầu của văn phạm
29
Ví dụ 3.6: Cho văn phạm :
S a A B e
A A b c | b
B d
Câu abbcde có thể thu gọn về S theo các bước sau:
a b b c d e
a A b c d e
a A d e
a A B e
S
Đảo ngược lại quá trình trên ta thu được dẫn xuất phải nhất:
S rm aABe rm aAde rm aAbcde rm abbcde
30
Handles: Handle của một right-sentential form là một luật sinh A , một xâu sao cho = và S * rm A rm . Đôi khi ta còn gọi là một handle, xâu bên phải chỉ chứa các kí hiệu kết thúc
Nếu một văn phạm là không mơ hồ thì với mỗi right-sentential form có duy nhất một handle của nó
Ví dụ 3.7: Trong dẫn xuất S rm aABe rm aA d e rm a Abc de rm a b bcde các handle được gạch chân
31
Ví dụ 3.8: Xét văn phạm mơ hồ
E E + E | E * E | (E) | id
Với cùng một biểu thức id+id*id sẽ có hai dẫn xuất phải nhất (các handle được gạch chân). Cùng một right sentence form E+E*id3 trong trường hợp đầu id3 là handle còn trường hợp thứ 2 handle là E+E
E rm E + E
rm E + E * E
rm E + E * id3
rm E + id2 * id3
rm id1 + id2 * id3
E rm E * E
rm E * id3
rm E + E * id3
rm E + id2 * id3
rm id1 + id2 * id3
32
Biểu diễn stack của shift- reduce parsing
STACK
INPUT
ACTION
$
$ id 1
$ E
$ E +
$ E + id 2
$ E + E
$ E + E *
$ E + E * id 3
$ E + E * E
$ E + E
$ E
id 1 + id 2 * id 3 $
+ id 2 * id 3 $
+ id 2 * id 3 $
id 2 * id 3 $
* id 3 $
* id 3 $
id 3 $
$
$
$
$
shift
reduce by E id
shift
shift
reduce by E id
shift
shift
reduce by E id
reduce by E E * E
reduce by E E + E
accept
33
Phân tích cú pháp LR (LR parser)
LR(k) là một kỹ thuật phân tích cú pháp từ dưới lên hiệu quả, có thể sử dụng để phân tích một lớp rộng các văn phạm phi ngữ cảnh.
- L ( L eft-to-right): Duyệt chuỗi nhập từ trái sang phải
- R ( R ightmost derivation): Xây dựng chuỗi dẫn xuất phải nhất đảo ngược
- k :Số lượng ký hiệu lookahead tại mỗi thời điểm, dùng để đưa ra quyết định phân tích. Khi không đề cập đến k, chúng ta hiểu ngầm là k = 1
34
Ưu điểm của LR:
- Có thể nhận biết hầu như tất cả các ngôn ngữ lập trình được tạo ra bởi văn phạm phi ngữ cảnh
- Phương pháp phân tích cú pháp LR là phương pháp tổng quát của phương pháp shift-reduce không quay lui
- Lớp văn phạm có thể dùng phương pháp LR là một lớp rộng lớn hơn lớp văn phạm có thể sử dụng phương pháp dự đoán
Có thể xác định lỗi cú pháp nhanh ngay trong khi duyệt dòng nhập từ trái sang phải
Nhược điểm của LR:
- Xây dựng LR parser khá phức tạp
35
Mô hình của LR parser
LR parsing
program
OUTPUT
INPUT
STACK
s o
...
X m-1
s m-1
X m
s m
$
a n
....
a i
....
a 1
goto
action
Parsing table
36
STACK lưu chuỗi s 0 X 1 s 1 X 2 s 2 ... X m s m trong đó s m nằm trên đỉnh STACK một ký hiệu văn phạm, s i là một trạng thái tóm tắt thông tin chứa trong STACK bên dưới nó
Parsing table bao gồm 2 phần : Hàm action và hàm goto
- action[s m , a i ] có thể có một trong 4 giá trị :
1. shift s : Đẩy s, trong đó s là một trạng thái
2. reduce : Thu gọn bằng luật sinh A
3. accept : Chấp nhận
4. error : Báo lỗi
- goto lấy 2 tham số là một trạng thái và một ký hiệu văn phạm, nó sinh ra một trạng thái
37
Cấu hình (configuration) của một bộ phân tích cú pháp LR là một cặp thành phần
(s 0 X 1 s 1 X 2 s 2 ... X m s m , a i a i+1 ... a n $). Cấu hình biểu diễn right- sentential form X 1 X 2 ... X m a i a i+1 ... a n
Sự thay đổi cấu hình theo hàm action như sau:
- Nếu action[s m , a i ] = shift s, cấu hình chuyển thành
(s 0 X 1 s 1 X 2 s 2 ... X m s m a i s, a i+1 ... a n $), trong đó
s=action[s m , a i ]
- Nếu action[s m , a i ] = reduce A , cấu hình chuyển thành
(s 0 X 1 s 1 X 2 s 2 ... X m-r s m-r A s, a i a i+1 ... a n $), trong đó s=goto[s m-r , A], r=| |=|X m-r+1 ....X m |
- Nếu action[s m , a i ] = accept, quá trình phân tích thành công
- Nếu action[s m , a i ] = error, gọi thủ tục phục hồi lỗi
38
(1) E E + T
State
Action
Goto
(2) E T
id
+
*
(
)
$
E
T
F
(3) T T * F
0
s 5
S 4
1
2
3
(4) T F
1
s 6
acc
(5) F (E)
2
r 2
s 7
r 2
r 2
(6) F id
3
r 4
r 4
r 4
r 4
4
s 5
s 4
8
2
3
Ý nghĩa :
5
r 6
r 6
r 6
r 6
s i : shift s i
6
s 5
s 4
9
3
r j : reduce by production j
7
s 5
s 4
10
acc : accept
8
s 6
s 11
blank: error
9
r 1
s 7
r 1
r 1
10
r 3
r 3
r 3
r 3
11
r 5
r 5
r 5
r 5
Ví dụ 3.9: Xét văn phạm cho các phép toán số học + và *
39
STACK
INPUT
ACTION
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
0
0 id 5
0 F 3
0 T 2
0 T 2 * 7
0 T 2 * 7 id 5
0 T 2 * 7 F 10
0 T 2
0 E 1
0 E 1 + 6
0 E 1 + 6 id 5
0 E 1 + 6 F 3
0 E 1 + 6 T 9
0 E 1
id * id + id $
* id + id $
* id + id $
* id + id $
id + id $
+ id $
+ id $
+ id $
+ id $
id $
$
$
$
$
shift
reduce by F ® id
reduce by T ® F
shift
shift
reduce by F ® id
reduce by T ® T * F
reduce by E ® T
shift
shift
reduce by F ® id
reduce by T ® F
reduce by E ® E + T
accept
Với chuỗi nhập id*id+id quá trình phân tích như sau:
40
Xây dựng SLR parsing table
Có 3 phương pháp xây dựng một bảng phân tích cú pháp LR từ văn phạm là Simple LR (SLR), Canonical LR và Lookahead- LR (LALR), các phương pháp khác nhau về tính hiệu quả cũng như tính dễ cài đặt
Phương pháp SLR, là phương pháp yếu nhất nếu tính theo số lượng văn phạm có thể xây dựng thành công, nhưng đây lại là phương pháp dễ cài đặt nhất
Một văn phạm có thể xây dựng được SLR parser được gọi là một văn phạm SLR
41
Một mục LR(0) (hoặc item) của một văn phạm G là một luật sinh của G với một dấu chấm tại vị trí nào đó trong vế phải
Ví dụ 3.10: Luật sinh A XYZ có 4 mục như sau:
A .XYZ
A X.YZ
A XY.Z
A XYZ.
Luật sinh A chỉ tạo ra một mục A .
42
Văn phạm tăng cường (Augmented Grammar): G là một văn phạm với ký hiệu bắt đầu S, thêm một ký hiệu bắt đầu mới S' và luật sinh S' S để được văn phạm mới G' gọi là văn phạm tăng cường
Phép toán bao đóng (Closure): Giả sử I là một tập các mục của văn phạm G thì bao đóng closure(I) là tập các mục được xây dựng từ I như sau:
1. Tất cả các mục của I được thêm vào closure(I).
2. Nếu A .B closure(I) và B là một luật sinh thì thêm B . vào closure(I) nếu nó chưa có trong đó. Lặp lại bước này cho đến khi không thể thêm vào closure(I) được nữa
43
Ví dụ 3.11: Xét văn phạm tăng cường
E' E
E E + T | T
T T * F | F
F (E) | id
Nếu I= {E' · E} thì closure(I) bao gồm các mục sau:
E' · E
E · E + T
E · T
T · T * F
T · F
F · (E)
F · id
44
Phép toán goto: Nếu I là một tập các mục và X là một ký hiệu văn phạm thì goto(I, X) là bao đóng của tập hợp các mục A X. sao cho A . X I
Cách tính goto(I, X):
1. Tạo một tập I' =
2. Nếu A . X I thì đưa A X. vào I', tiếp tục quá trình này cho đến khi xét hết tập I.
3. goto(I, X) = closure(I')
45
Ví dụ 3.12: Giả sử I = { E' E., E E . + T }
Ta có I' = { E E + . T }
goto (I, +) = closure(I') bao gồm các mục :
E E + . T
T . T * F
T . F
F . (E)
F . id
46
Giải thuật xây dựng họ tập hợp các mục LR(0) (kí hiệu là C) của văn phạm G'
procedure Item (G')
begin
C := {closure({ S' . S}) };
repeat
For Với mỗi tập các mục I C và mỗi ký hiệu văn phạm X sao cho goto (I, X) và
goto(I, X) C thì thêm goto(I, X) vào C;
until Không còn tập hợp mục nào có thể thêm vào C;
end;
47
Ví dụ 3.13: Xây dựng họ tập hợp các mục trong ví dụ 3.11
closure({E' E}) I 0 :
goto ( I 0 , E) I 1 :
goto ( I 0 , T) I 2 :
goto (I 0 ,F) I 3 :
goto (I 0 , ( ) I 4 :
E' · E
E · E + T
E · T
T · T * F
T · F
F · (E)
F · id
E' E ·
E E · + T
E T ·
T T · * F
T F ·
F (· E)
E · E + T
E · T
T · T * F
T · F
F · (E)
F · id
goto ( I 0 , id) I 5 :
goto ( I 1 , +) I 6 :
goto ( I 2 , *) I 7 :
goto ( I 4 , E) I 8 :
goto ( I 6 ,T) I 9 :
goto ( I 7 ,F) I 10 :
goto (I 8 ,) ) I 11 :
F id ·
E E + · T
T · T * F
T · F
F · (E)
F · id
T T* · F
F · (E)
F · id
F (E ·)
E E · + T
E E + T ·
T T · * F
T T * F ·
F (E) ·
48
Xây dựng SLR parsing table
1. Xây dựng họ tập hợp các mục của G': C = { I 0 , I 1 , ..., I n }
2. Trạng thái i được xây dựng từ I i .Các action tương ứng trạng thái i xác định như sau:
a) Nếu A .a I i và goto (I i , a) = I j thì action[i, a] = "shift j",
a là ký hiệu kết thúc
b) Nếu A . I i thì action[i, a] = "reduce (A ) ", với mọi a FOLLOW(A), A S'
c) Nếu S' S · I i thì action[i, $] = "accept".
Nếu một action đụng độ được sinh ra bởi các luật trên, ta nói văn phạm không phải là SLR(1). Giải thuật thất bại
3. Nếu goto (I i ,A)=I j thì goto [i, A] = j, A là kí hiệu chưa kết thúc
4. Các ô không xác định được bởi 2 và 3 đều là “error”
5. Trạng thái khởi đầu của bộ phân tích cú pháp được xây dựng từ tập các mục chứa S’ · S
49
Xây dựng bảng phân tích LR chính tắc
LR chính tắc (canonical LR) là kĩ thuật chung nhất để xây dựng LR parsing table cho một văn phạm
Một mục LR(1) (item) là một cặp [A ., a] trong đó A là một luật sinh, a- là kí tự lookahead là một kí hiệu kết thúc hoặc $
Nếu thì a không có ý nghĩa nhưng nếu = thì việc reduce theo luật A chỉ được thực hiện nếu kí tự đọc vào tiếp theo là a
50
Phép toán bao đóng (Closure): Giả sử I là một tập các mục LR(1) của văn phạm G thì bao đóng closure(I) là tập các mục được xây dựng từ I như sau:
1. Tất cả các mục của I được thêm vào closure(I).
2. Nếu [A .B, a] closure(I), B là một luật sinh và b FIRST( a) thì thêm [B ., b] vào closure(I) nếu nó chưa có trong đó. Lặp lại bước này cho đến khi không thể thêm vào closure(I) được nữa
Phép toán goto: Nếu I là một tập các mục và X là một ký hiệu văn phạm thì goto(I, X) là bao đóng của tập hợp các mục [A X. , a] sao cho [A . X , a] I
51
Giải thuật xây dựng họ tập hợp các mục LR(1) (kí hiệu là C) của văn phạm G'
procedure Item (G')
begin
C := {closure({[ S' . S, $ ]})};
repeat
For Với mỗi tập các mục I C và mỗi ký hiệu văn phạm X sao cho goto (I, X) và
goto(I, X) C thì thêm goto(I, X) vào C;
until Không còn tập hợp mục nào có thể thêm vào C;
end;
52
closure({S' S }) I 0 :
goto ( I 0 , S) I 1 :
goto ( I 0 , C) I 2 :
goto (I 0 , c) I 3 :
S' · S, $
S · CC, $
C · cC, c/d
C · d, c/d
S' S ·, $
S C ·C, $
C · cC, $
C · d, $
C c ·C, c/d
C · cC, c/d
C · d, c/d
goto (I 0 , d ) I 4 :
goto ( I 2 , C) I 5 :
goto ( I 2 , c) I 6 :
goto ( I 2 , d) I 7 :
goto ( I 3 , C) I 8 :
goto ( I 6 ,C) I 9 :
C d ·, c/d
S CC ·, $
C c · C, $
C · cC, $
C · d, $
C d ·, $
C cC ·, c/d
C cC ·, $
Ví dụ 3.14: Xây dựng họ tập hợp các mục LR(1) cho văn phạm dưới đây
S' S
(1) S CC
(2) C cC
(3) C d
53
Xây dựng canonical LR parsing table
1. Xây dựng họ tập hợp các mục LR(1) của G': C = {I 0 , I 1 ,.., I n }
2. Trạng thái i được xây dựng từ I i .Các action tương ứng trạng thái i xác định như sau:
a) Nếu [A .a, b] I i và goto (I i , a) = I j thì action[i, a] = "shift j", a là ký hiệu kết thúc
b) Nếu [A ., a] I i thì action[i, a] = "reduce (A .) ", A S'
c) Nếu [S' S ·, $] I i thì action[i, $] = "accept".
Nếu một action đụng độ được sinh ra bởi các luật trên, ta nói văn phạm không phải là LR(1). Giải thuật thất bại
3. Nếu goto (I i ,A)=I j thì goto [i, A] = j, A là kí hiệu chưa kết thúc
4. Các ô không xác định được bởi 2 và 3 đều là “error”
5. Trạng thái khởi đầu của bộ phân tích cú pháp được xây dựng từ tập các mục chứa [S’ · S, $]
54
State
Action
Goto
c
d
$
S
C
0
s3
s4
1
2
1
acc
2
s6
s7
5
3
s3
s4
8
4
r3
r3
5
r1
6
s6
s7
9
7
r3
8
r2
r2
9
r2
Canonical LR parsing table cho văn phạm trong ví dụ 3.14
55
LALR là phương pháp canonical parsing trong đó các trạng thái được nhóm lại với nhau nhờ đó bảng phân tich cấu trúc có kích thước nhỏ hơn (có thể so sánh với SLR)
Hạt nhân (core) của một tập hợp mục LR(1) có dạng {[A . , a ]}, trong đó A là một luật sinh và a là ký hiệu kết thúc có hạt nhân (core) là tập hợp {A . }.
Trong họ tập hợp các mục LR(1) C = {I 0 , I 1 ,..., I n } có thể có các tập hợp các mục có chung một hạt nhân.
Xây dựng bảng phân tích LALR
56
Xây dựng LALR parsing table
1. Xây dựng họ tập hợp các mục LR(1) của G': C = {I 0 , I 1 ,.., I n }
2. Nhóm các mục có cùng core trong C được C' = {J 0 , J 1 ,.., J m }
3. Trạng thái i được xây dựng từ J i .Các action tương ứng trạng thái i xác định tương tự như canonical LR
Nếu một action đụng độ được sinh ra bởi các luật trên, ta nói văn phạm không phải là LALR(1). Giải thuật thất bại
3. Xây dựng bảng goto : Giả sử J = I 1 I 2 . I k . Vì I 1 , I 2 , ... I k có chung hạt nhân nên goto (I 1 ,X), goto (I 2 ,X), ..., goto (I k ,X) cũng có chung hạt nhân.
Ðặt K bằng hợp tất cả các tập hợp có chung hạt nhân với goto (I1,X) khi đó goto(J, X) =K.
57
State
Action
Goto
c
d
$
S
C
0
s36
s47
1
2
1
acc
2
s36
s47
5
36
s36
s47
89
47
r3
r3
r3
5
r1
89
r2
r2
r2
LALR parsing table cho văn phạm trong ví dụ 3.14
58
Công cụ phân tích cú pháp Yacc
Giống như Lex, Yacc (yet another compiler compiler) là câu lệnh sẵn có của UNIX và là một công cụ hữu hiệu cho phép xây dựng bộ phân tích cú pháp một cách tự động
Yacc được tạo bởi S. C. Johnson vào những năm đầu của thập kỉ 70
Yacc sử dụng phương pháp LALR
59
Yacc specification
translate.y
Yacc
compiler
y.tab.c
y.tab.c
C
compiler
a.out
input
a.out
output
60
File đính kèm:
 bai_giang_chuong_trinh_dich_chuong_3_phan_tich_cu_phap.ppt
bai_giang_chuong_trinh_dich_chuong_3_phan_tich_cu_phap.ppt

