Bài giảng Chương trình dịch - Chương 2: Phân tích từ vựng
Vai trò của phân tích từ vựng
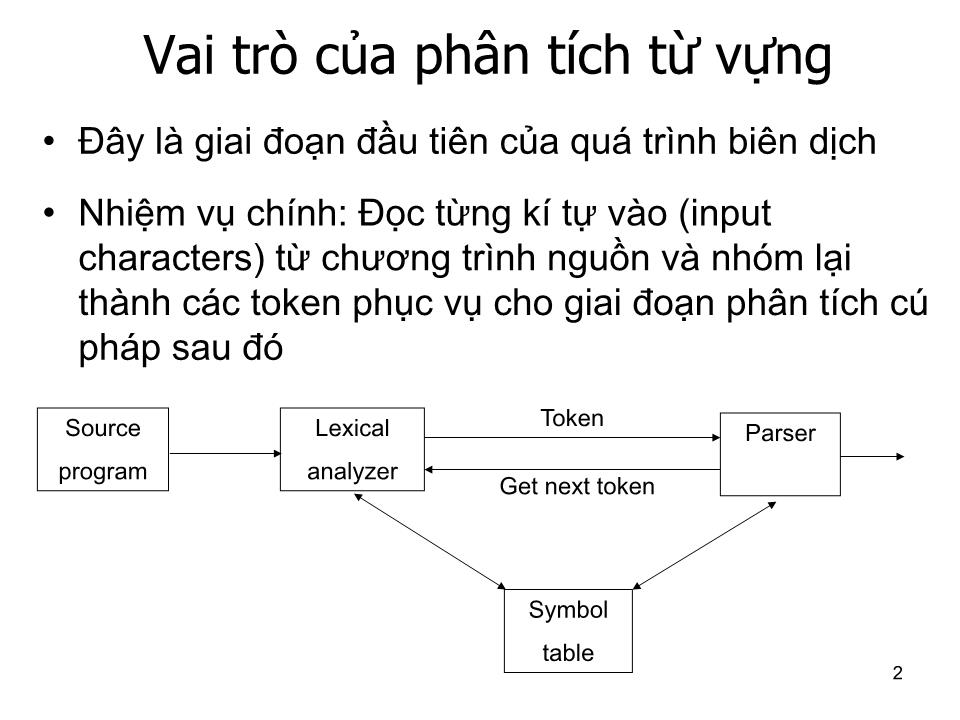
Đây là giai đoạn đầu tiên của quá trình biên dịch
Nhiệm vụ chính: Đọc từng kí tự vào (input characters) từ chương trình nguồn và nhóm lại thành các token phục vụ cho giai đoạn phân tích cú pháp sau đó
Phân tích từ vựng giúp cho các giai đoạn biên dịch tiếp theo dễ dàng hơn, ví dụ: Giai đoạn phân tích cú pháp không phải quan tâm đến các khoảng trắng cũng như các lời chú trích vì nó đã được loại bỏ khi khi phân tích từ vựng
Giảm đáng kể thời gian đọc chương trình nguồn và nhóm thành các token nhờ một số chương trình xử lí chuyên dụng
Một số khái niệm
Token: Một token là một tập hợp các xâu kí tự có một nghĩa xác định, ví dụ identifier token là tập hợp tất cả các identifier. Token chính là các kí hiệu kết thúc (terminal) trong định nghĩa văn phạm của một ngôn ngữ, ví dụ: Các từ khoá, định danh, toán tử, hằng, xâu kí tự, dấu ngoặc đơn, dấu phẩy, dấu chấm phẩy.
Pattern: Pattern của một token là các qui tắc kết hợp các kí tự để tạo lên token đó
Lexeme: Là một chuỗi các kí tự thoả mãn pattern của một token

Trang 1
Trang 2

Trang 3

Trang 4
Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Chương trình dịch - Chương 2: Phân tích từ vựng

CHƯƠNG II
Phân tích từ vựng
Mục tiêu: Nắm được vai trò của giai đoạn phân tích từ vựng, sử dụng các khái niệm biểu thức chính qui (regular expression) và ô- tô- mát hứu hạn (finite automata) trong việc biểu diễn và nhận biết ngôn ngữ
1
Vai trò của phân tích từ vựng
Đây là giai đoạn đầu tiên của quá trình biên dịch
Nhiệm vụ chính: Đọc từng kí tự vào (input characters) từ chương trình nguồn và nhóm lại thành các token phục vụ cho giai đoạn phân tích cú pháp sau đó
Source
program
Lexical
analyzer
Get next token
Token
Parser
Symbol
table
2
Phân tích từ vựng giúp cho các giai đoạn biên dịch tiếp theo dễ dàng hơn, ví dụ: Giai đoạn phân tích cú pháp không phải quan tâm đến các khoảng trắng cũng như các lời chú trích vì nó đã được loại bỏ khi khi phân tích từ vựng
Giảm đáng kể thời gian đọc chương trình nguồn và nhóm thành các token nhờ một số chương trình xử lí chuyên dụng
3
Một số khái niệm
Token: Một token là một tập hợp các xâu kí tự có một nghĩa xác định, ví dụ identifier token là tập hợp tất cả các identifier. Token chính là các kí hiệu kết thúc (terminal) trong định nghĩa văn phạm của một ngôn ngữ, ví dụ: Các từ khoá, định danh, toán tử, hằng, xâu kí tự, dấu ngoặc đơn, dấu phẩy, dấu chấm phẩy...
Pattern: Pattern của một token là các qui tắc kết hợp các kí tự để tạo lên token đó
Lexeme: Là một chuỗi các kí tự thoả mãn pattern của một token
4
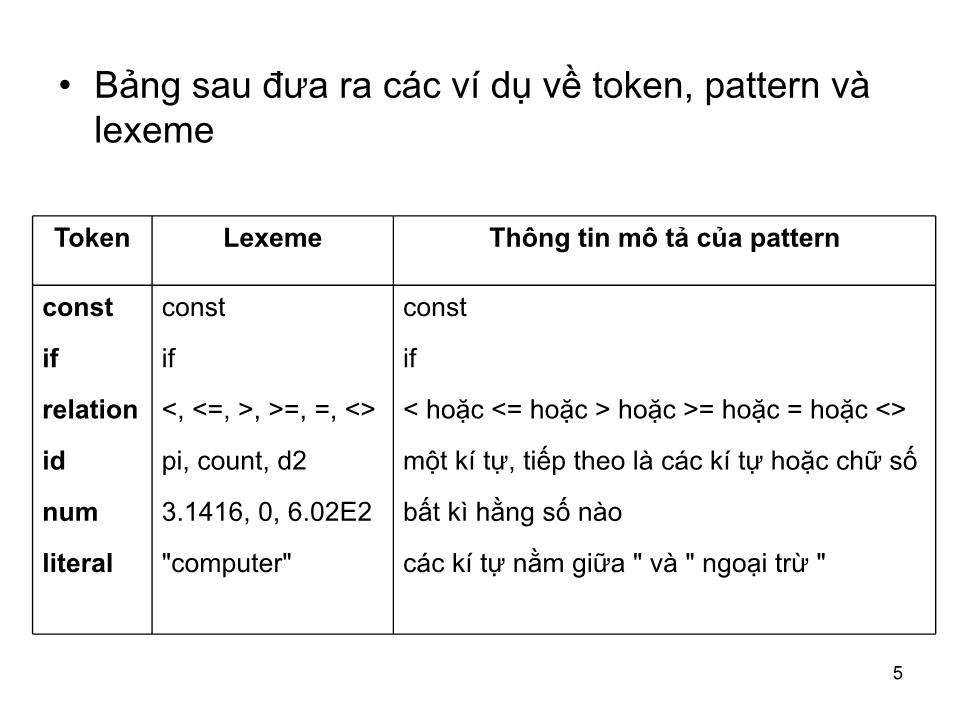
Bảng sau đưa ra các ví dụ về token, pattern và lexeme
Token
Lexeme
Thông tin mô tả của pattern
const
if
relation
id
num
literal
const
if
, >=, =,
pi, count, d2
3.1416, 0, 6.02E2
"computer"
const
if
hoặc >= hoặc = hoặc
một kí tự, tiếp theo là các kí tự hoặc chữ số
bất kì hằng số nào
các kí tự nằm giữa " và " ngoại trừ "
5
Đặc tả Token
Xâu kí tự (string): Là một chuỗi các kí tự từ một bảng chữ cái. Kí hiệu xâu rỗng là
Một số khái niệm liên quan đến xâu kí tự: Tiền tố (prefix), hậu tố (suffix), xâu con (substring), tiền tố thực sự (proper prefix)....
Ngôn ngữ (language): Là tập hợp các xâu kí tự được xây dựng từ một bảng chữ cái
6
Các phép toán trên ngôn ngữ: Giả sử L và M là hai ngôn ngữ khi đó
Hợp (union)của L và M: L M={s|s L hoặc s M }
Ghép (concatenation) của L và M: LM = { st | s L và t M }
Bao đóng Kleen (kleene closure) L: L* = i=0 L i
(Ghép của 0 hoặc nhiều L)
Bao đóng dương (positive closure) của L: L + = i=1 L i (Ghép của 1 hoặc nhiều L)
7
Ví dụ: L = {A, B, ..., Z, a, b, ..., z } và
D = { 0, 1, , ..., 9 }
1. L D là tập hợp các chữ cái và chữ số
2. LD là tập hợp các xâu bao gồm một chữ cái và một chữ số
3. L 4 là tập hợp tất cả các xâu 4 chữ cái
4. L * là tâp hợp tất cả các xâu của các chữ cái bao gồm cả chuỗi rỗng
5. L(L D)* là tập hợp tất cả các xâu mở đầu bằng một chữ cái theo sau là chữ cái hay chữ số
6. D + là tập hợp tất cả các xâu gồm một hoặc nhiều chữ số
8
Biểu thức chính qui
(regular expression)
Mỗi biểu thức chính qui (BTCQ) r dùng để đặc tả một ngôn ngữ L(r).
Ví dụ: Trong pascal mọi identifier được đặc tả bởi biểu thức chính qui letter(letter|digit) *
Hai BTCQ r và s được gọi là tương đương (kí hiệu r=s) nếu chúng đặc tả chung một ngôn ngữ
Ví dụ: (a|b)=(b|a)
Một BTCQ được xây dựng từ những BTCQ đơn giản bằng cách sử dụng các luật
9
Sau đây là các luật định nghĩa các BTCQ trên một bảng chữ cái
1. là một BTCQ đặc tả {} (tập hợp chứa xâu rỗng)
2. Nếu a thì a là BTCQ đặc tả {a}
3. Giả sử r và s là các BTCQ đặc tả các ngôn ngữ L(r) và L(s), khi đó:
a) (r)|(s) là một BTCQ đặc tả L(r) L(s)
b) (r)(s) là một BTCQ đặc tả L(r)L(s)
c) (r) * là một BTCQ đặc tả (L(r)) *
d) (r) là một BTCQ đặc tả L(r)
10
Ví dụ: Cho = { a, b}.
1. BTCQ a | b đặc tả {a, b}
2. BTCQ (a | b) (a | b) đặc tả {aa, ab, ba, bb}.Tập hợp này có thể được đặc tả bởi BTCQ tương đương sau: aa | ab | ba | bb
3. BTCQ a * đặc tả { , a, aa, aaa, ... }
4. BTCQ (a | b)* đặc tả {a, b, aa,bb, ...}. Tập hợp này có thể đặc tả bởi (a*b* )*
5. BTCQ a | a* b đặc tả {a, b, ab, aab,... }
11
Định nghĩa chính qui
(regular definition)
Để thuận tiện về mặt kí hiệu, ta dùng định nghĩa chính qui (ĐNCQ) để đặt tên cho các BTCQ
Một ĐNCQ là một dãy các định nghĩa có dạng
d 1 r 1
d 2 r 2
.........
d n r n
Trong đó d i là các tên, r i là các BTCQ trên tập các kí hiệu {d 1 , d 2 , ....d i-1 }
12
Ví dụ: ĐNCQ của các định danh trong pascal là
letter A | B | ...| Z | a | b |...| z
digit 0 | 1 | ...| 9
id letter (letter | digit)*
Ví dụ: ĐNCQ của các số không dấu trong pascal như 3254, 23.243E5,16.264E-3... là
digit 0 | 1 |...| 9
digits digit digit*
optional_fraction . digits | e
optional_exponent ( E ( + | - | e ) digits) | e
num digits optional_fraction optional_exponent
13
Các kí hiệu tắt được sử dụng trong các BTCQ
+: Một hoặc nhiều
?: Không hoặc một
Ví dụ: ĐNCQ cho tập số không dấu được viết lại như sau
digit 0 | 1 |...| 9
digits digit +
optional_fraction (. digits) ?
optional_exponent ( E ( + | - ) ? digits) ?
num digits optional_fraction optional_exponent
Sử dụng các tập kí tự [abc]=a | b | c, [a-z]=a | b |..z ta có thể đặc tả các định danh bởi BTCQ
[A - Z a - z] [A - Z a - z 0 - 9]*
14
Nhận dạng token
Làm thế nào để nhận dạng được token? Ta sẽ xét 1 ví dụ mang tính chất minh hoạ
Ví dụ: Cho ngữ pháp (grammar)
stmt if expr then stmt
| if expr then stmt else stmt
|
expr term relop ter m
| term
term id
| num
15
Trong đó các kí hiệu kết thúc (token) if, then, else, relop, id sinh ra tập các xâu kí tự theo các ĐNCQ sau:
if if
then then
else else
relop | > | >=
id letter ( letter | digit ) *
num digit + ( . digit +) ? ( E ( + | - ) ? digit + ) ?
Các kí tự khoảng trắng (loại bỏ khi phân tích từ vựng) được định nghĩa bởi ĐNCQ sau:
delim blank | tab | newline
ws delim +
16
Mục đích của lexical analyzer tạo ra output là các cặp
Regular Expression
Token
Attribute-value
ws
-
-
if
if
-
then
then
-
else
else
-
id
id
pointer to table entry
num
num
pointer to table entry
<
relop
LT
<=
relop
LE
=
relop
EQ
relop
NE
>
relop
GT
>=
relop
GE
17
Sơ đồ chuyển tiếp (transition diagram): Là bước trung gian minh hoạ tiến trình chuyển đổi trạng thái khi bộ phân tích từ vựng đọc lần lượt từng kí tự
Ta phải xây dựng các sơ đồ chuyển tiếp để nhận biết từng loại token
Một sơ đồ chuyển tiếp bao gồm các trạng thái (states) được vẽ bằng hình tròn, có 1 trạng thái bắt đầu (start state). Các trạng thái được nối với nhau bởi các mũi tên ta gọi là các cạnh (edges)
Trạng thái được biểu diễn bởi vòng tròn kép là trạng thái được chấp nhận (accepting state) thông báo 1 token đã được nhận dạng
18
Ví dụ: Sơ đồ chuyển tiếp cho token các toán tử quan hệ relop
0
8
7
6
5
4
3
2
1
return (relop, LE )
return (relop, NE )
return (relop, LT )
return (relop, EQ )
return (relop, GE )
return (relop, GT )
*
*
<
=
>
other
=
>
=
other
start
19
Ví dụ: Sơ đồ chuyển tiếp cho token các identifier và keyword
Chú ý:
- Các từ khoá là các từ được bảo vệ và được lưu trữ sẵn trong symbol-table
- Thủ tục gettoken() tra cứu lexeme trong symbol-table nếu là 1 keyword thì token tương ứng được trả về còn ngược lại token id được trả về
- Thủ tục install_id() tra cứu lexeme trong symbol-table nếu là 1 keyword thì trả lại giá trị 0, nếu là một biến đã có thì trả lại một con trỏ tới vị trí trong symbol-table. Nếu lexeme không có thì tạo một phần tử mới trong symbol-table và trả về con trỏ tới thành phần mới vừa được tạo
9
11
10
return ( gettoken(), install_id() )
letter
start
letter or digit
other
*
20
Ví dụ: Sơ đồ chuyển tiếp cho token các unsigned numbers trong pascal
*
12
14
digit
start
.
18
digit
15
digit
13
digit
19
17
16
+ or -
E
other
digit
digit
E
digit
20
22
digit
start
.
23
digit
21
digit
24
other
digit
*
25
digit
start
26
digit
27
other
*
21
Ví dụ: Sơ đồ chuyển tiếp cho token các ws
28
delim
start
29
delim
30
other
*
22
Công cụ phân tích từ vựng Lex
Một số công cụ có sẵn cho phép xây dựng một bộ phân tích từ vựng dựa trên các biểu thức chính qui
Một trong số những công cụ đó là Lex compiler (một công cụ có sẵn của Unix)
Sơ đồ sau chỉ rõ cách tạo một bộ phân tích từ vựng bằng cách sử dụng Lex
23
Lex source program lex.l
Lex
compiler
Lex.yy.c
lex.yy.c
C
compiler
a.out
input stream
a.out
sequence of tokens
24
Ô- tô- mát hữu hạn
(finite automata)
Một bộ nhận dạng ngôn ngữ (recognizer for a language) là một chương trình nhận đầu vào là một xâu kí tự x, trả lời "Yes" nếu x thuộc ngôn ngữ và trả lời "No" nếu ngược lại
Ô- tô- mát hữu hạn là một sơ đồ chuyển tiếp được khái quát hoá, đóng vai trò là recognizer cho các biểu thức chính qui
Một Ô- tô- mát hữu hạn có thể là deterministic finite automata (DFA) hoặc nondeterministic finite automata (NFA)
25
"Nondeterministic" nghĩa là khi một kí tự được đọc vào thì sơ đồ chuyển tiếp có thể chuyển đến nhiều hơn một trạng thái tiếp theo
Cả hai DFA và NFA đều có khả năng nhận dạng các biểu thức chính qui
DFA có thể nhận dạng nhanh hơn nhưng cũng có kích thước lớn hơn NFA tương đương
26
NFA
Một NFA là một mô hình toán học bao gồm:
- Một tập hợp trạng thái S
- Một trạng thái bắt đầu s 0 S
- Một tập hợp các trạng thái chấp nhận (hoặc trạng thái kết thúc) FS
- Một tập hợp kí tự vào của bảng chữ cái
- Một hàm chuyển đổi trạng thái move: S x ({}) S
(Một phép chuyển đổi (s k , ) s j nghĩa là chuyển từ s k sang s j mặc dù không có kí tự nào được đọc vào)
NFA được biểu diễn trực tiếp bằng sơ đồ chuyển tiếp
27
Ví dụ: NFA nhận biết BTCQ (a|b) * abb được mô tả dưới đây trong đó tập S={0, 1, 2, 3}, ={a, b}, s 0 =0 và trạng thái kết thúc là 3 (vòng tròn kép)
Hàm chuyển đổi trạng thái theo bảng dưới đây
0
a
start
2
1
a
3
b
b
b
Trạng thái
Kí tự vào
a
b
0
{0, 1}
{0}
1
-
{2}
2
-
{3}
28
Ví dụ: NFA nhận biết biểu thức chính qui aa * | bb *
0
a
start
2
1
a
4
b
b
3
29
DFA
DFA là một trường hợp đặc biệt của NFA, DFA có thêm các dặc diểm sau:
- Không có chuyển đổi trạng thái ứng với kí tự rỗng
- Từ một trạng thái s khi có một kí tự x được đọc vào, DFA sẽ chuyển sang một trạng thái s' duy nhất
30
Ví dụ: DFA nhận biết BTCQ (a|b) * abb
0
b
start
2
1
a
3
a
b
b
b
a
a
31
File đính kèm:
 bai_giang_chuong_trinh_dich_chuong_2_phan_tich_tu_vung.ppt
bai_giang_chuong_trinh_dich_chuong_2_phan_tich_tu_vung.ppt

