Bài giảng Các thuật toán tìm kiếm
Bài toán tìm kiếm mở rộng
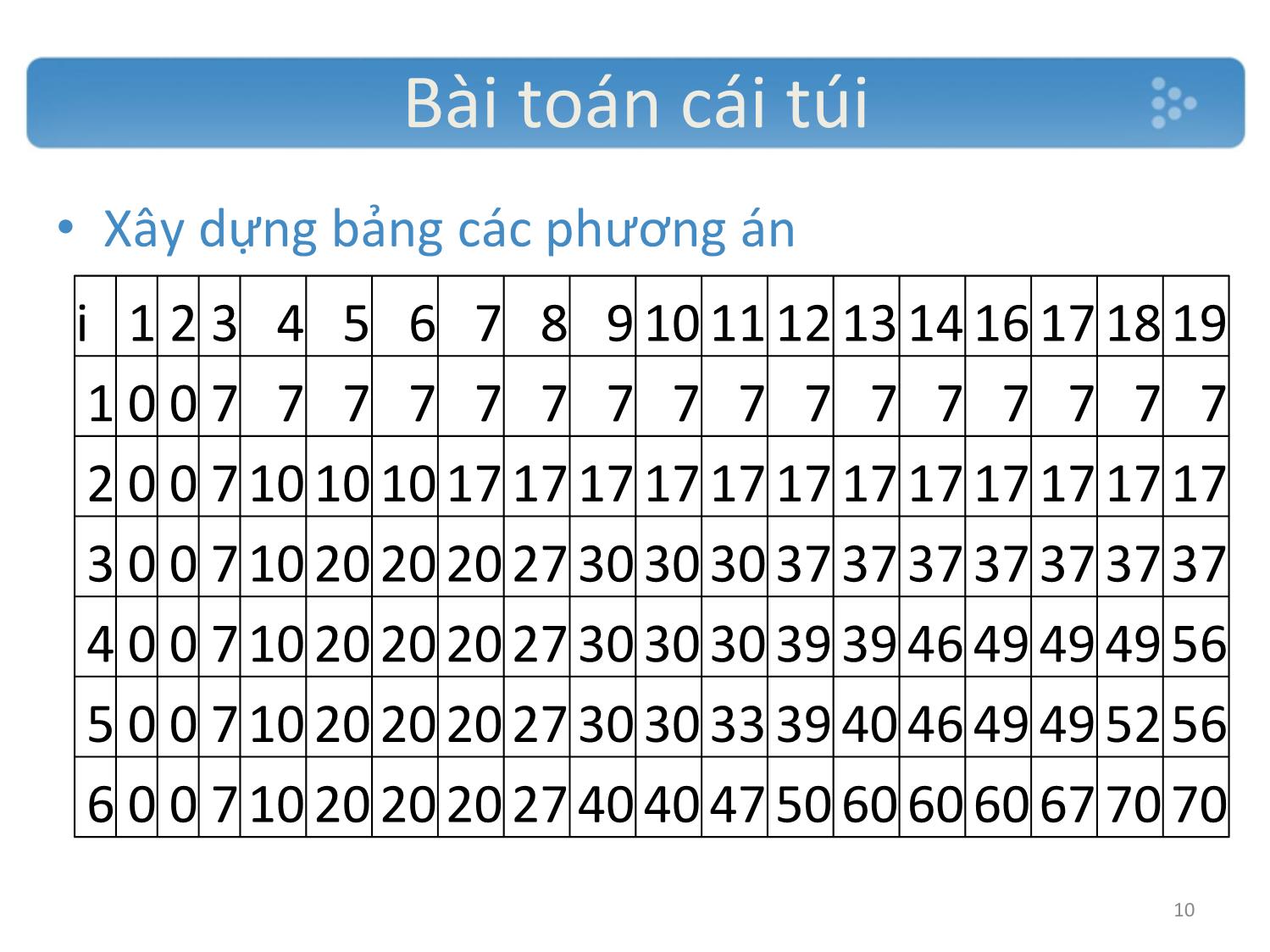
• Tìm kiếm trên quy hoạch động
Bài toán cái túi cơ bản
• Tìm kiếm bằng đệ quy
Sử dụng thuật toán đệ quy cho bài toán cái túi
• Tìm kiếm phân vùng tìm kiếm
Phân tích quá trình chia vùng tìm kiếm với bài toán
cái túi
3Bài toán cái túi
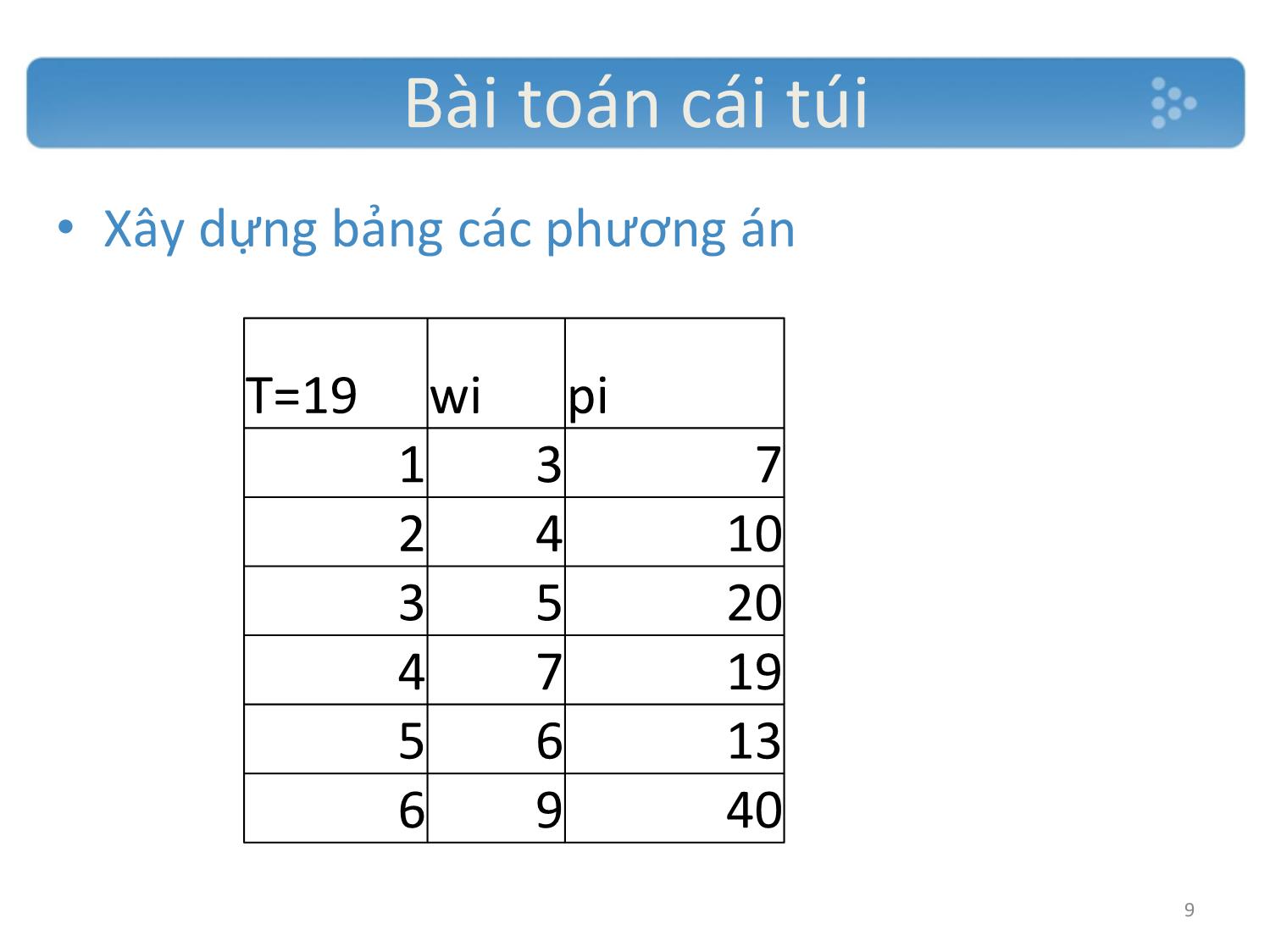
• Tìm kiếm phương án lấy đồ cho cái túi
Một tên trộm mang túi có thể mang được trụng
lượng là C
Đến một ngôi nhà có N vật, mỗi vật có trọng lượng
là là w
i và có giá trị là pi
Tìm các đồ vật mà tên trộm có thể lấy được mà có
tổng giá trị lớn nhất
4Bài toán cái túi
• Tiếp cận quy hoạch động
Dựa trên mô tả về U(k,i) = max(U(k-wk)+pk,U(k-1,i))
• Tiếp cận tổ hợp
Sử dụng các phương án có thể, kiểm tra lấy giá trị
lớn nhất (sử dụng đệ quy

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Các thuật toán tìm kiếm

Giới thiệu Các thuật toán tìm kiếm 1 Nội dung trình bày • Bài toán tìm kiếm • Tìm kiếm tuần tự, tìm kiếm nhị phân Tìm kiếm tuần tự Tìm kiếm nhị phân • Một số tiếp cận khác Tìm kiếm dựa trên quy hoạch động Tìm kiếm dựa trên đệ quy Tìm kiếm dựa trên phân vùng 2 Bài toán tìm kiếm mở rộng • Tìm kiếm trên quy hoạch động Bài toán cái túi cơ bản • Tìm kiếm bằng đệ quy Sử dụng thuật toán đệ quy cho bài toán cái túi • Tìm kiếm phân vùng tìm kiếm Phân tích quá trình chia vùng tìm kiếm với bài toán cái túi 3 Bài toán cái túi • Tìm kiếm phương án lấy đồ cho cái túi Một tên trộm mang túi có thể mang được trụng lượng là C Đến một ngôi nhà có N vật, mỗi vật có trọng lượng là là wi và có giá trị là pi Tìm các đồ vật mà tên trộm có thể lấy được mà có tổng giá trị lớn nhất 4 Bài toán cái túi • Tiếp cận quy hoạch động Dựa trên mô tả về U(k,i) = max(U(k-wk)+pk,U(k-1,i)) • Tiếp cận tổ hợp Sử dụng các phương án có thể, kiểm tra lấy giá trị lớn nhất (sử dụng đệ quy) 5 Bài toán cái túi • Thuật toán xây dựng phương án buildsolution • Input: T, w[N], p[N] • Output: Ma trận PA • for(i=T->w[0]) PA[0,i]=p[0]; • For(i=0->w[0]-1) PA[0,i]=0; 6 Bài toán cái túi • Thuật toán xây dựng phương án buildsolution (t) • For(i=1->N-1) For(j=T->w[i]) • PA[i,j]=max(PA[i-1,j], PA[i-1,j-w[i]]+p[i]) For(j=w[i]-1->0) • PA[i,j]=PA[i-1,j]; 7 Bài toán cái túi • Thuật toán xây dựng phương án getsolution • Input: PA[N,T], w[N], p[N] • Output: các vật cần lấy • i=N • j=T • While(i>0 &&j>0) If(PA[i,j]!PA[i-1,j]) • Print(i) • J=j-w[i]; i=i-1; • If(PA[i,j]!=0) print(i) 8 Bài toán cái túi • Xây dựng bảng các phương án 9 T=19 wi pi 1 3 7 2 4 10 3 5 20 4 7 19 5 6 13 6 9 40 Bài toán cái túi • Xây dựng bảng các phương án 10 i 1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 18 19 1 0 0 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 2 0 0 7 10 10 10 17 17 17 17 17 17 17 17 17 17 17 17 3 0 0 7 10 20 20 20 27 30 30 30 37 37 37 37 37 37 37 4 0 0 7 10 20 20 20 27 30 30 30 39 39 46 49 49 49 56 5 0 0 7 10 20 20 20 27 30 30 33 39 40 46 49 49 52 56 6 0 0 7 10 20 20 20 27 40 40 47 50 60 60 60 67 70 70 Bài toán cái túi • Xây dựng bảng các phương án 11 i 1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 18 19 1 0 0 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 2 0 0 7 10 10 10 17 17 17 17 17 17 17 17 17 17 17 17 3 0 0 7 10 20 20 20 27 30 30 30 37 37 37 37 37 37 37 4 0 0 7 10 20 20 20 27 30 30 30 39 39 46 49 49 49 56 5 0 0 7 10 20 20 20 27 30 30 33 39 40 46 49 49 52 56 6 0 0 7 10 20 20 20 27 40 40 47 50 60 60 60 67 70 70 Bài toán cái túi • Tiếp cận đệ quy Sinh tổ hợp để xét 12 Bài toán cái túi • Phân tích xu hướng phân vùng để tìm kiếm với bài toán cái túi 13 14 Bài tập - Cài đặt thuật toán trên ngôn ngữ lập trình và chạy thử
File đính kèm:
 bai_giang_cac_thuat_toan_tim_kiem.pdf
bai_giang_cac_thuat_toan_tim_kiem.pdf

