10 Đề ôn tập thi THPT Quốc gia năm 2021 môn Toán
Câu 1. Cho hàm số y = f(x) xác định trên khoảng (−2; 5) và có đạo hàm f 0(x) > 0; 8x 2 (−2; 5). Trong
các mệnh đề sau, mệnh đề nào đúng?
A. f(−2) < f(3). B. f(−2) < f(5). C. f(4) < f(5). D. f(−1) < f(4).
Câu 2. Tính thể tích V của khối trụ có chiều cao bằng h và bán kính đáy bằng R.
A. V = 2πRh. B. V = πRh. C. V = R2h. D. V = πR2h.
Câu 3. Tập xác định của hàm số y = (x − 1)
15
là
A. (1; +1). B. (0; +1). C. [1; +1). D. R n f1g.
Câu 4. Cho hàm số y = 2x3 + 6x + 2. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng (−1; +1).
B. Hàm số nghịch biến trên khoảng (−1; 0) và đồng biến trên khoảng (0; +1).
C. Hàm số nghịch biến trên khoảng (−1; +1).
D. Hàm số đồng biến trên khoảng (−1; 0) và nghịch biến trên khoảng (0; +1).

Trang 1

Trang 2

Trang 3

Trang 4
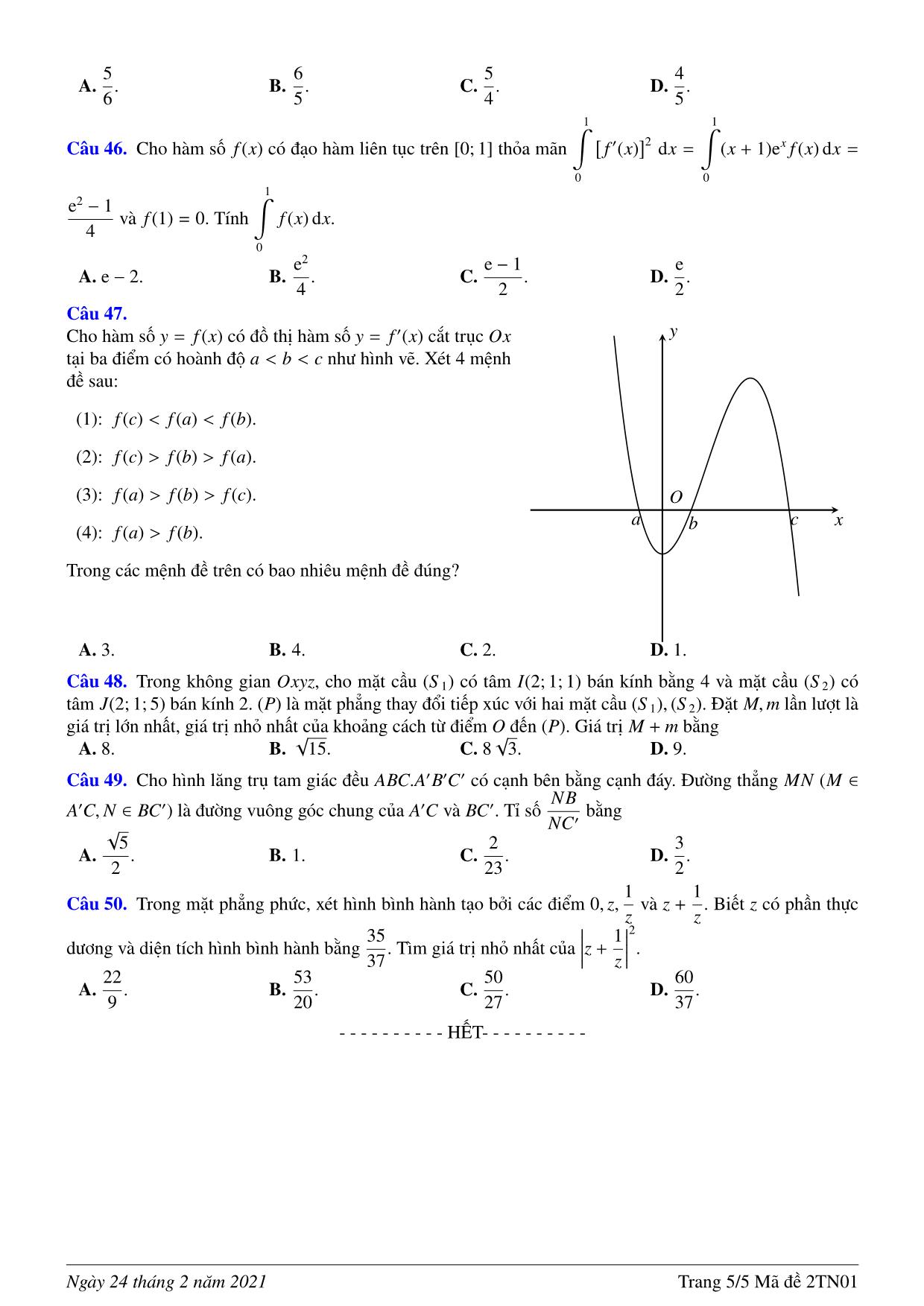
Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: 10 Đề ôn tập thi THPT Quốc gia năm 2021 môn Toán

hần thực của z bằng 3, phần ảo của z bằng 2.
Chọn đáp án D
Câu 8. Theo định nghĩa ta có: Nếu m là giá trị nhỏ nhất của hàm số f (x) trên đoạn [a; b] thì f (x) ≥ 0 với
mọi x ∈ [a; b]. Vậy đây là mệnh đề đúng.
Chọn đáp án A
Câu 9. Trên đoạn [1; 2] ta có f ′(x) = 1 − 16
(1 + 2x)2
. Khi đó
f ′(x) = 0⇔ 4x2 + 4x − 15 = 0⇔
x =
3
2
x = −5
2
< (1; 2)
.
Ta có f (1) =
11
3
; f (2) =
18
5
; f
(
3
2
)
=
7
2
. Suy ra min
x∈[1;2]
f (x) =
7
2
và max
x∈[1;2]
f (x) =
11
3
.
Chọn đáp án C
Câu 10. Ta có log 3
√
8
5
=
1
3
log
16
10
=
1
3
(
4 log 2 − 1) = 4a − 1
3
.
Chọn đáp án D
104
Câu 11. Số tiền không thay đổi, lãi suất không thay đổi nên thời gian tăng gấp 3 thì số tiền tăng lên
(1,37)3 = 2,74.
Chọn đáp án D
Câu 12. Xét hàm số y = 2x3 + 6x + 2 có tập xác định D = R.
Có y′ = 6x2 + 6 > 0 với ∀x ∈ R⇒ hàm số đã cho đồng biến trên tập xác định.
Chọn đáp án D
Câu 13.
Diện tích tam giác ABC là
a2
2
.
Thể tích V của hình chóp S .ABC là
V =
1
3
· a
2
2
· a√2 = a
3
√
2
6
.
S
B C
A D
Chọn đáp án A
Câu 14.
Ta có S tp = 2piRh + 2pir2 = 2pi · a · a
√
3 + 2 · pia2 = 2pia2(1 + √3).
O
O′
Chọn đáp án A
Câu 15.
B
C
D
A
H
Gọi H là trọng tâm tam giác BCD và G là tâm mặt cầu nội tiếp tứ diện ABCD.
Khi đó bán kính mặt cầu nội tiếp tứ diện ABCD là
r = d (G, (ABC)) = d (G, (BCD)) = d (G, (ACD)) = d (G, (ABD))
Ta có VG.BCD =
1
3
· S BCD · d (G, (BCD))⇒ d (G, (BCD)) = 3 · VG.BCDS BCD .
Mà VG.BCD = VG.ABC = VG.ABD = VG.ACD vì S BCD = S ABC = S ABD = S ACD.
Mặt khác VG.BCD + VG.ABC + VG.ABD + VG.ACD = VABCD ⇒ VG.BCD = 14VABCD.
Do BH =
a
√
3
3
, AH =
√
AB2 − BH2 = a
√
6
3
nên VABCD =
a3
√
2
12
⇒ VG.BCD = a
3
√
2
48
.
Vậy r = d (G, (BCD)) =
3 · VG.BCD
S BCD
=
a
√
6
12
.
Chọn đáp án D
105
Câu 16. Ta có x = 2 sin t ⇒ dx = 2 cos t dt.
Với x = 0⇒ t = 0, x = 1⇒ t = pi
6
.
Do đó I =
pi
6∫
0
2 cos t dt√
4 − 4 sin2 t
=
pi
6∫
0
2 cos t dt
2
√
cos2 t
=
pi
6∫
0
2 cos t dt
2 cos t
=
pi
6∫
0
dt.
Chọn đáp án A
Câu 17. Gọi B(x; y; z), suy ra ~AB = (x − 4; y − 6; z + 3).
~AB = ~a⇔
x − 4 = −3
y − 6 = 2
z + 3 = 1
⇔
x = 1
y = 8
z = −2.
Vậy B(1; 8;−2).
Chọn đáp án C
Câu 18. Gọi (Q) là mặt phẳng cần tìm.
Ta có ~AB = (1;−1;−1) và véc-tơ pháp tuyến của (P) là ~nP = (1;−3; 2).
Véc-tơ pháp tuyến của (Q) là ~n =
[
~nP, ~AB
]
= (5; 3; 2).
Mặt phẳng (Q) qua B(2; 1; 0) có phương trình (Q) : 5(x − 2) + 3(y − 1) + 2(z − 0) = 0
⇔ 5x + 3y + 2z − 13 = 0.
Chọn đáp án B
Câu 19. Đặt z = x + yi với x, y ∈ R.
Ta có
|(1 + 2i)z − 10| = |(2 + i)z + 5|
⇔ |(1 + 2i)(x + yi) − 10| = |(2 + i)(x − yi) + 5|
⇔ |x − 2y − 10 + (2x + y)i| = |(2x + y) + (x − 2y + 5)i|
⇔ (x − 2y − 10)2 + (2x + y)2 = (2x + y)2 + (x − 2y + 5)2
⇔ 2x − 4y − 5 = 0.
Suy ra tập hợp các điểm biểu diễn cho số z là đường thẳng 2x − 4y − 5 = 0.
Chọn đáp án C
Câu 20. Ta có
1
z
=
1
mi
= − i
m
⇒ phần ảo của 1
z
là − 1
m
·
Chọn đáp án C
Câu 21.
Ta có CD ‖ (S AB)⇒ d(CD, S B) = d(CD, (S AB)) = d(D, (S AB)).
DA ⊥ (S AB)⇒ d(D, (S AB)) = DA = AC√
2
= a
√
2.
S
DA
B C
Chọn đáp án B
106
Câu 22.
Ta có
d(M, (ABC))
d(S , (ABC))
=
MA
SA
=
2
3
⇒ d(M, (ABC)) = 6.
Lại có
d(N, (ABC))
d(S , (ABC))
=
NA
S A
=
1
2
⇒ d(N, (ABC)) = 9
2
.
Vậy d(M, (ABC)) + d(N, (ABC)) = 6 +
9
2
=
21
2
.
S
A
B
N
M
C
Chọn đáp án C
Câu 23. Không gian mẫu Ω = {NN,NS , S N, S S }.
Gọi A là biến cố mặt ngửa xuất hiện ít nhất 1 lần. Khi đó A = {NN,NS , S N} ⇒ n(A) = 3.
Chọn đáp án C
Câu 24. Xác suất để lần gieo thứ nhất là mặt lẻ là
1
2
Xác suất để lần gieo thứ hai là mặt lẻ là
1
2
Xác suất để lần gieo thứ ba là mặt lẻ là
1
2
.
Suy ra xác suất cả ba lần gieo đều xuất hiện mặt lẻ là
1
2
· 1
2
· 1
2
=
1
8
.
Chọn đáp án B
Câu 25. Ta có u1 = 3 và q =
u2
u1
=
15
3
= 5. Từ đó x = u4 = u1.q3 = 3.53 = 375.
Chọn đáp án A
Câu 26. Xét hàm số y = 2x3 + 6x + 2 có tập xác định D = R.
Có y′ = 6x2 + 6 > 0 với ∀x ∈ R⇒ hàm số đã cho đồng biến trên tập xác định.
Chọn đáp án D
Câu 27. Ta có lim
x→±∞ y = limx→±∞
(a2 − 9)x2 − 4
ax − √9x2 + 4
. Để giới hạn này tồn tại hữu hạn thì a2 − 9 = 0⇔ a = ±3.
Thử lại:
- Với a = 3 thì lim
x→+∞
(a2 − 9)x2 − 4
ax − √9x2 + 4
= 0. Tiệm cận ngang y = 0.
- Với a = −3 thì lim
x→−∞
(a2 − 9)x2 − 4
ax − √9x2 + 4
= 0. Tiêm cận ngang y = 0
Chọn đáp án B
Câu 28.
• Ta có: y′ = 4ax3 + 2bx = 2x
(
2ax2 + b
)
.
• Từ hình vẽ, suy ra đồ thị hàm số có 3 điểm cực trị có tọa độ là (−1;−4), (0;−3), (1;−4).
• Khi đó:
y(0) = −3
y (−1) = y(1) = −4
y′ (−1) = y′(1) = 0
⇔
c = −3
a + b + c = −4
2a + b = 0
⇔
a = 1
b = −2
c = −3.
Chọn đáp án B
107
Câu 29. lim
x→+∞
√
(3k + 1)x2 + 1
x
= 9 f ′(2)⇔ √3k + 1 = 4⇔ k = 5.
Chọn đáp án A
Câu 30. Điều kiện x > 0.
Ta có
log23 x − 2 log3 x + 1 − m2 = 0⇔
[
log3 x = 1 − m
log3 x = 1 + m
⇔
x = 31−m
x = 31+m.
Theo đề bài, ta có
x1 + x2 = 10 ⇔ 31−m + 31+m = 10⇔ 3 · 32m − 10 · 3m + 3 = 0
⇔
3
m = 3
3m =
1
3
⇔
[
m = 1
m = −1.
Kết hợp với điều kiện x1 < x2 suy ra x1 =
1
3
và x2 = 9.
Vậy x2 − 3x1 = 6.
Chọn đáp án D
Câu 31. Điều kiện
5x − 1 > 05x+1 − 5 > 0 ⇔ 5x − 1 > 0⇔ x > 0.
Khi đó,
log5 (5
x − 1) log25
(
5x+1 − 5
)
≤ 1
⇔ log5 (5x − 1)
[
1 + log5 (5
x − 1)] ≤ 2
⇔ log25 (5x − 1) + log5 (5x − 1) − 2 ≤ 0
⇔ − 2 ≤ log5 (5x − 1) ≤ 1
⇔ 1
25
≤ 5x − 1 ≤ 5
⇔ 26
25
≤ 5x ≤ 6
⇔ log5
26
25
≤ x ≤ log5 6.
Đối chiếu với điều kiện, tập nghiệm của bất phương trình đã cho là S =
[
log5
26
25
; log5 6
]
.
Suy ra a = log5
26
25
, b = log5 6.
Vậy a + b = log5
26
25
+ log5 6 = log5 26 − 2 + log5 6 = −2 + log5 156.
Chọn đáp án C
Câu 32.
108
Gọi M là trung điểm CD. Do ACD và BCD là những tam giác
đều, ta dễ dàng chứng minh được CD ⊥ (ABM).
Trong (ABM), vẽ AH ⊥ BM tại H, suy ra AH ⊥ (BCD).
Ta có
VABCD =
1
3
AH.S BCD =
1
3
.AH.
√
3
4
.(2
√
3)2 =
√
3AH.
Vậy để thể tích khối tứ diện ABCD là lớn nhất thì AH phải lớn
nhất. Mặt khác, AH ≤ AM = 3 và dấu bằng xảy ra khi H ≡ M.
Nếu H ≡ M thì khi đó,
x = AB =
√
AH2 + BH2 =
√
AM2 + BM2 =
√
9 + 9 = 3
√
2.
A
B
C
D
M
H
x
Chọn đáp án B
Câu 33.
Gọi M,N, I lần lượt là trung điểm AB,CD và MN. Ta có
∆ABC = ∆BAD ⇒ MC = MD ⇒ ∆MCD cân tại M ⇒ MN ⊥ CD
(1)
Tương tự MN ⊥ AB (2)
Từ (1) và (2), suy ra MN là đường trung trực của AB và CD.
Do đó IA = IB = IC = ID ⇒ I là tâm mặt cầu ngoại tiếp tứ diện
ABCD.
Dùng công thức độ dài đường trung tuyến ta có MC2 =
2(b2 + c2) − a2
4
C
D
N
A
B
M
I
MN =
√
MC2 −CN2 =
√
b2 + c2 − a2
2
⇒ IN = 1
2
√
b2 + c2 − a2
2
Suy ra bán kính R = IC =
√
IN2 +CN2 =
1
2
√
2
√
a2 + b2 + c2.
Chọn đáp án A
Câu 34. Xét I =
∫
f (x) dx =
∫
1 + ln x
x2
dx.
Đặt
u = 1 + ln x
dv =
1
x2
dx
⇒
du =
1
x
dx
v = −1
x
. Khi đó
I = −1
x
(1 + ln x) +
∫
1
x2
dx = −1
x
(1 + ln x) − 1
x
+C = −1
x
(ln x + 2) +C ⇒ a = −1; b = 2.
Vậy S = a + b = 1.
Chọn đáp án A
Câu 35. Đặt t = a − x⇒ dx = − dt.
⇒ I =
∫ a
0
1
1 + f (a − t) dt =
∫ a
0
1
1 +
1
f (x)
dx =
∫ a
0
f (x)
1 + f (x)
dx.
⇒ 2I =
∫ a
0
dx = a⇒ I = a
2
.
Chọn đáp án D
Câu 36. Dựa vào hình vẽ, ta có
S =
2∫
0
√
x dx +
4∫
2
(√
x − x + 2
)
dx =
2
3
x
3
2
∣∣∣∣∣2
0
+
(
2
3
x
3
2 − x
2
2
+ 2x
)∣∣∣∣∣∣4
2
=
10
3
.
109
Chọn đáp án B
Câu 37.
Theo đề bài ta có OA = OB =
√
2 và
S ODE =
1
2
S OAB
⇔1
2
· OD · OE · sin D̂OE = 1
2
· 1
2
· OA · OB · sin ÂOB
⇔OD · OE = 1
2
OA · OB = 1. O D A
I
M
E
B
Mặt khác
DE2 = OD2 + OE2 − 2OD.OE. cos ÂOB ≥ 2OD.OE − 2OD.OE. cos ÂOB = 2
(
1 − cos ÂOB
)
.
Suy ra DE nhỏ nhất khi OD = OE = 1.
Gọi M là trung điểm của AB, ta có M
(
1
2
;
1
2
; 0
)
.
Khi đó,
−→
OI =
OI
OM
· −−→OM = OD
OA
· −−→OM =
√24 ;
√
2
4
; 0
. Suy ra I √24 ;
√
2
4
; 0
Chọn đáp án C
Câu 38. Giả sử A(a; 0; 0), B(0; b; 0), C(0; 0; c), abc , 0. Khi đó mặt phẳng (α) có dạng:
x
a
+
y
b
+
z
c
= 1.
Ta có:
−−→
AH = (1 − a; 2;−2), −−→BH = (1; 2 − b;−2), −→BC = (0;−b; c), −→AC = (−a; 0; c).
H là trực tâm tam giác ABC nên
1
a
+
2
b
+
−2
c
= 1
− 2b − 2c = 0
− a − 2c = 0
⇔
a = 9
b =
9
2
c = −9
2
.
Vậy phương trình của (α) :
x
9
+
2y
9
− 2z
9
= 1⇔ x + 2y − 2z − 9 = 0.
Bán kính mặt cầu là R = d(O, (α)) = 3.
Phương trình mặt cầu: x2 + y2 + z2 = 9.
Chọn đáp án B
Câu 39. d1 có véc-tơ chỉ phương −→u1 = (−1; 1; 1) và đi qua điểm A(2; 0; 0). Đường thẳng d2 có véc-tơ chỉ
phương −→u2 = (2;−1;−1) và đi qua điểm B(0; 1; 2).
[−→u1,−→u2] = (0; 1;−1), trung điểm của AB là I (1; 12; 1
)
.
Mặt phẳng (P) song song và cách đều hai đường thẳng d1, d2 suy ra (P) đi qua I và có véc-tơ pháp tuyến là
(0; 1;−1).
Do đó phương trình của mặt phẳng (P) là y − 1
2
− (z − 1) = 0⇔ 2y − 2z + 1 = 0.
Chọn đáp án C
Câu 40. z4 + 3z2 + 4 = 0.
Đặt X = z2. Khi đó phương trình trở thành X2 + 3X + 4 = 0
Theo định lý Vi-ét ta có
{
S = X1 + X2 = −3
P = X1 · X2 = 4
Ta có: X1 = X2.
P = X1 · X2 = X1 · X1 = |X1|2 = |z2|2 = 4⇒ |z2| = 2.
Do đó T = 4 · |z2| = 4 · 2 = 8.
Chọn đáp án D
Câu 41. Gọi x, y, z (x, y, z > 0) lần lượt là chiều dài, chiều rộng và chiều cao của hồ nước.
Theo giả thiết, ta có
x = 2y
V = xyz =
500
3
⇔
x = 2y
z =
250
3y2
·
110
Diện tích xây dựng của hồ nước là S = xy + 2xz + 2yz = 2y2 + 6yz = 2y2 +
500
y
·
Chi phí thuê nhân công thấp nhất khi diện tích nhỏ nhất.
Xét hàm số f (y) = 2y2 +
500
y
với y > 0.
Ta có f ′(y) = 4y − 500
y2
=
4
(
y3 − 125
)
y2
; f ′(y) = 0⇔ y3 − 125 = 0⇔ y = 5.
Bảng biến thiên
y
f ′(y)
f (y)
0 5 +∞
− 0 +
+∞
150
+∞
Dựa vào bảng biến thiên ta thấy S nhỏ nhất khi y = 5.
Suy ra kích thước của hồ là x = 10 m; y = 5 m, z =
10
3
m. Tiền thuê nhân công là 75 triệu đồng.
Chọn đáp án D
Câu 42. Đồ thị hàm số y = |x3 − 3x2 +m| có 5 điểm cực trị⇔ đồ thị hàm số y = x3 − 3x2 +m cắt trục hoành
tại ba điểm phân biệt⇔ hai điểm cực trị của đồ thị hàm số y = x3 − 3x2 + m khác phía so với Ox.
Các giá trị cực trị của hàm số y = x3 − 3x2 + m là f (0) = m và f (2) = m − 4.
Hai điểm cực trị khác phía so với Ox⇔ f (0) · f (2) < 0⇔ 0 < m < 4.
Do đó, S = {1; 2; 3} nên tổng các phần tử của S là 6.
Chọn đáp án C
Câu 43. Ta có y′ =
x√
x2 + 3
− (ln x + 1) < x√
x2
− (ln x + 1) < − ln x < 0, ∀x ∈ [1; 2].
Do đó, hàm số y =
√
x2 + 3 − x ln x nghịch biến trên [1; 2].
Vậy Mm = y(1) · y(2) = 2
(√
7 − 2 ln 2
)
= 2
√
7 − 4 ln 2.
Chọn đáp án C
Câu 44. Ta có
2sin
2 x + 2cos
2 x = m⇔ 2sin2 x + 2
2sin2 x
= m.
Đặt t = 2sin
2 x ta có 0 ≤ sin2 x ≤ 1⇒ 1 ≤ 2sin2 x ≤ 2 hay t ∈ [1; 2].
Xét hàm f (t) = t +
2
t
với t ∈ [1; 2].
Có f ′(t) = 1 − 2
t2
⇒ f ′(t) = 0⇔
t =
√
2
t = −√2
.
Bảng biến thiên
t
f ′(t)
f (t)
1
√
2 2
− 0 +
3
2
√
2
3
111
Mà phương trình trên tương đương với f (t) = m.
Do đó để phương trình có nghiệm thì m ∈ [2√2; 3].
Chọn đáp án A
Câu 45.
Thể tích VO.MNPQ =
1
3
d (O, (MNPQ)) · S MNPQ.
Gọi E, F, I, J lần lượt là trung điểm của AB, BC, CD,
DA. Ta có PQ ‖ IJ và PQ = 2
3
IJ.
Hai hình bình hành MNPQ và EFIJ đồng dạng với tỉ số
đồng dạng k =
2
3
.
Suy ra,
S MNPQ
S EFIJ
= k2 ⇒ S MNPQ = 49S EFIJ.
mà S EFIJ =
1
2
S ABCD ⇒ S MNPQ = 29S ABCD.
Mặt khác, do (MNPQ) ‖ (ABCD) nên
A
B
S
C
D
PM
N
Q
I
O
J
E
F
d (O, (MNPQ)) = d (P, (ABCD)) =
1
3
d (S , (ABCD)).
Do đó
VS .ABCD =
1
3
d (S , (ABCD)) · S ABCD
=
1
3
· 3 d (O, (MNPQ)) · 9
2
S MNPQ
=
27
2
· 1
3
d (O, (MNPQ)) · S MNPQ = 272 V.
Chọn đáp án A
Câu 46. Đặt f (x) =
sin2018 x
sin2018 x + cos2018 x
.
Đặt t = pi − x.
pi∫
0
x f (x) dx = −
0∫
pi
(pi − t) f (pi − t) dt
=
pi∫
0
(pi − t) f (pi − t) dt =
pi∫
0
(pi − x) f (pi − x) dx =
pi∫
0
(pi − x) f (x) dx
=
pi∫
0
pi f (x) dt −
pi∫
0
x f (x) dt.
Suy ra
pi∫
0
x f (x) dx =
pi
2
pi∫
0
f (x) dx.
112
Xét I1 =
pi∫
0
f (x) dx. Đặt t =
pi
2
− x.
I1 = −
−pi
2∫
pi
2
f (
pi
2
− t) dt =
pi
2∫
−pi
2
cos2018 t
cos2018 t + sin2018 t
dt = 2
pi
2∫
0
cos2018 t
cos2018 t + sin2018 t
dt
= 2
pi
2∫
0
cos2018 x
cos2018 x + sin2018 x
dx.
Xét I2 =
pi
2∫
0
cos2018 x
cos2018 x + sin2018 x
dx.
Đặt t =
pi
2
− x.
I2 =
pi
2∫
0
cos2018
(
pi
2
− t
)
cos2018
(
pi
2
− t
)
+ sin2018
(
pi
2
− t
) dt =
pi
2∫
0
sin2018 t
cos2018 t + sin2018 t
dt
=
pi
2∫
0
sin2018 x
cos2018 x + sin2018 x
dx.
Khi đó I1 = 2I2 = I2 + I2 =
pi∫
0
dx =
pi
2
. Suy ra
pi∫
0
x f (x) dx =
pi
2
I1 =
pi2
4
.
Suy ra a = 2; b = 4. Do đó 2a + b = 8.
Chọn đáp án B
Câu 47. Đường thẳng y = a cắt (P1) tại hai điểm có hoành độ −
√
4 − a và √4 − a. Vậy
S 1 =
√
4−a∫
−√4−a
(−x2 + 4 − a) dx = 4
3
· √4 − a · (4 − a).
Parabol (P2) có dạng y = m
(
x2 − 4
)
. Chú ý vì nó còn đi qua điểm (0; a) nên m = −a
4
. Vậy (P2) : y =
−a
4
x2 + a. Từ đó suy ra
S 2 =
2∫
−2
(
−a
4
x2 + a
)
dx =
8a
3
.
Từ đó ta có
16(4 − a)3
9
=
64a2
9
⇔ a3 − 8a2 + 48a = 64.
Chọn đáp án B
Câu 48.
113
z A
B
H
O
A′
C
Kiểm tra thấy hai điểm A, B nằm cùng phía so với bờ là mặt phẳng (P), trục Oz song song với mặt phẳng
(P).
Lấy điểm A′ đối xứng với A qua mặt phẳng (P). Ta có các đánh giá:
+ AB ≥ AB0 với B0 là hình chiếu của A lên trục Oz và AB0 có độ dài không đổi.
+ BC +CA = BC +CA′ ≥ A′B ≥ A′H, A′H có độ dài không đổi.
Từ đó suy ra
AB + BC +CA ≥ AB0 + A′H.
Dấu bằng xảy ra khi và chỉ khi B trùng B0(0; 0; 1).
Chọn đáp án C
Câu 49.
Mặt cầu (S ) có tâm I(1; 0;−1) và bán kính R = 1.{
IT ⊥ (P)⇒ IT ⊥ d
IT ′ ⊥ (P′)⇒ IT ′ ⊥ d ⇒ d ⊥ (ITT
′).
Gọi N = d ∩ (ITT ′)⇒ N là hình chiếu của I trên d.
Đường thẳng d có phương trình tham số
x = t
y = 2 + t
z = −t
t ∈ R
⇒ N (t; 2 + t;−t) và −→IN = (t − 1; 2 + t;−t + 1).
I T ′
T
H
N
−→
IN · ~u = 0⇔ t − 1 + 2 + t + t − 1 = 0⇔ t = 0⇒ N(0; 2; 0)⇒
IN =
√
6
−→
IN = (−1; 2; 1).
Ta có IH · IN = IT 2 ⇒ IH = 1√
6
.
Phương trình đường thẳng IN :
x = −u
y = 2 + 2u
z = u
⇒ H(−u; 2 + 2u; u) u ∈ R
và
−→
IH = (−u − 1; 2 + 2u; u + 1).
IH =
1√
6
⇔ IH2 = 1
6
⇔ (−u − 1)2 + (2u + 2)2 + (u + 1)2 = 1
6
⇔
u = −5
6
⇒ H
(
5
6
;
1
3
;−5
6
)
⇒ −→IH =
(
−1
6
;
1
3
;
1
6
)
u = −7
6
⇒ H
(
7
6
;−1
3
;−7
6
)
⇒ −→IH =
(
1
6
;−1
3
;−1
6
)
.
Vì
−→
IH cùng hướng với
−→
IN ⇒ H
(
5
6
;
1
3
;−5
6
)
.
114
Chọn đáp án B
Câu 50. Từ giả thiết ta có z = w, z = w và |z| = |w|.
Từ |z − w| = 2⇔ (z − w)(z − w) = 4⇔ |z|2 + |w|2 − zw − zw = 4⇔ 2|z|2 − z2 − z2 = 4 (∗).
Do
z
w2
là số thực nên
z
w2
=
z
w2
=
z
w2
. Từ đó suy ra
z
w2
=
w
z2
, hay
z3 = w3 ⇔ (z − w)(z2 − zw + w2) = 0.
Vậy z2 + w2 = zw = |z|2. Thay vào (∗) ta có
|z|2 = 4⇔ |z| = 2.
Chọn đáp án D
115
File đính kèm:
 10_de_on_tap_thi_thpt_quoc_gia_nam_2021_mon_toan.pdf
10_de_on_tap_thi_thpt_quoc_gia_nam_2021_mon_toan.pdf

