Ứng dụng phương pháp tán xạ tia X góc nhỏ đánh giá ảnh hưởng thăng giáng mật độ điện tử đến các cấu trúc vi mô của màng dẫn proton trong pin nhiên liệu

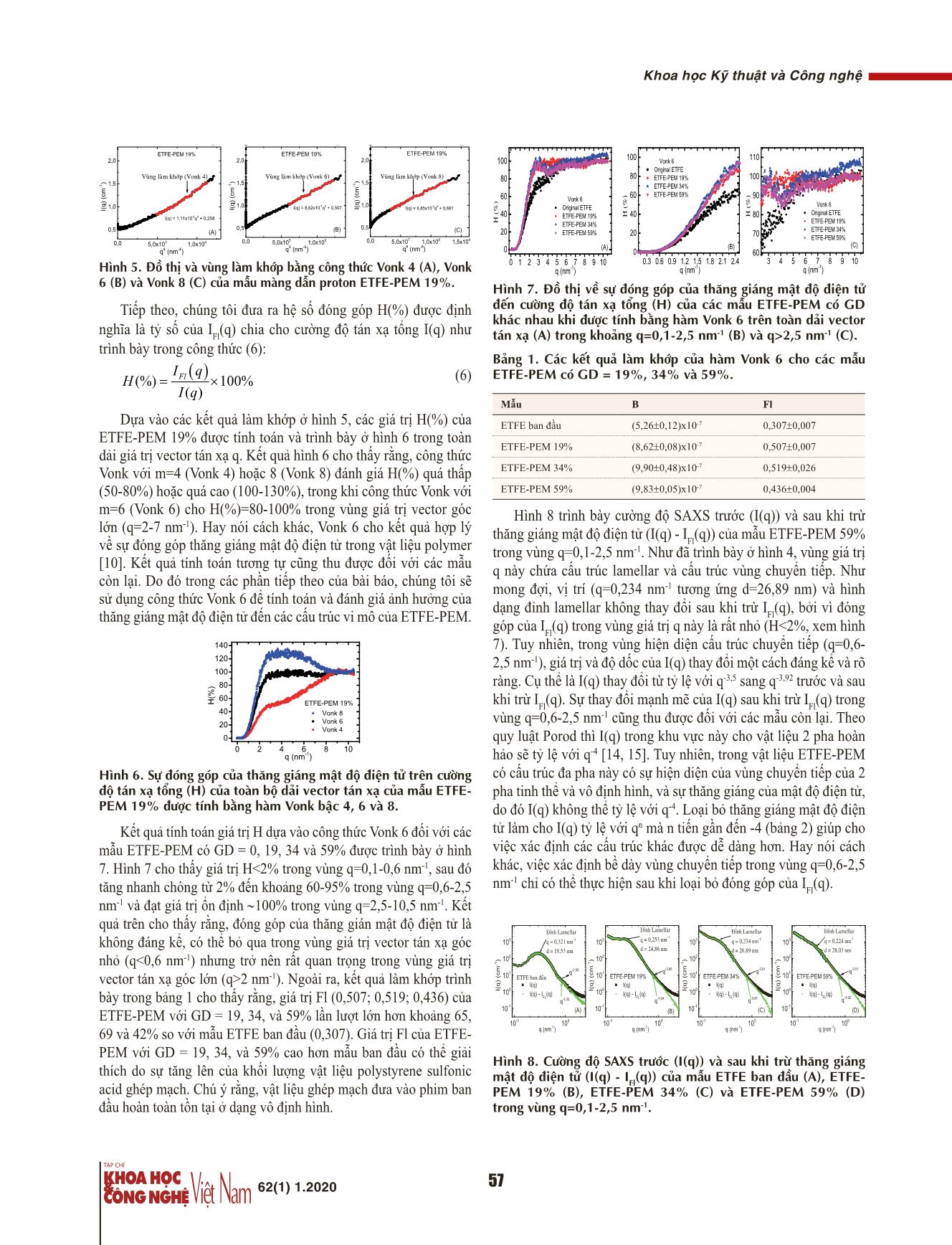
ép mạch. Chú ý rằng, vật liệu ghép mạch đưa vào phim ban 
đầu hoàn toàn tồn tại ở dạng vô định hình. 
0 1 2 3 4 5 6 7 8 9 10
0
20
40
60
80
100
 Vonk 6
 Original ETFE
 ETFE-PEM 19%
 ETFE-PEM 34%
 ETFE-PEM 59%
H
 (
%
)
q (nm-1)
(A)
0.3 0.6 0.9 1.2 1.5 1.8 2.1 2.4
0
20
40
60
80
100 Vonk 6
 Original ETFE
 ETFE-PEM 19%
 ETFE-PEM 34%
 ETFE-PEM 59%
H
 (
%
)
q (nm-1)
(B)
3 4 5 6 7 8 9 10
60
70
80
90
100
110
 Vonk 6
 Original ETFE
 ETFE-PEM 19%
 ETFE-PEM 34%
 ETFE-PEM 59%
H
 (
%
)
q (nm-1)
(C)
Hình 7. Đồ thị về sự đóng góp của thăng giáng mật độ điện tử 
đến cường độ tán xạ tổng (H) của các mẫu ETFE-PEM có GD 
khác nhau khi được tính bằng hàm Vonk 6 trên toàn dải vector 
tán xạ (A) trong khoảng q=0,1-2,5 nm-1 (B) và q>2,5 nm-1 (C).
Bảng 1. Các kết quả làm khớp của hàm Vonk 6 cho các mẫu 
ETFE-PEM có GD = 19%, 34% và 59%.
Mẫu B Fl
ETFE ban đầu (5,26±0,12)x10-7 0,307±0,007
ETFE-PEM 19% (8,62±0,08)x10-7 0,507±0,007
ETFE-PEM 34% (9,90±0,48)x10-7 0,519±0,026
ETFE-PEM 59% (9,83±0,05)x10-7 0,436±0,004
Hình 8 trình bày cường độ SAXS trước (I(q)) và sau khi trừ 
thăng giáng mật độ điện tử (I(q) - I
Fl
(q)) của mẫu ETFE-PEM 59% 
trong vùng q=0,1-2,5 nm-1. Như đã trình bày ở hình 4, vùng giá trị 
q này chứa cấu trúc lamellar và cấu trúc vùng chuyển tiếp. Như 
mong đợi, vị trí (q=0,234 nm-1 tương ứng d=26,89 nm) và hình 
dạng đỉnh lamellar không thay đổi sau khi trừ I
Fl
(q), bởi vì đóng 
góp của I
Fl
(q) trong vùng giá trị q này là rất nhỏ (H<2%, xem hình 
7). Tuy nhiên, trong vùng hiện diện cấu trúc chuyển tiếp (q=0,6-
2,5 nm-1), giá trị và độ dốc của I(q) thay đổi một cách đáng kể và rõ 
ràng. Cụ thể là I(q) thay đổi từ tỷ lệ với q-3,5 sang q-3,92 trước và sau 
khi trừ I
Fl
(q). Sự thay đổi mạnh mẽ của I(q) sau khi trừ I
Fl
(q) trong 
vùng q=0,6-2,5 nm-1 cũng thu được đối với các mẫu còn lại. Theo 
quy luật Porod thì I(q) trong khu vực này cho vật liệu 2 pha hoàn 
hảo sẽ tỷ lệ với q-4 [14, 15]. Tuy nhiên, trong vật liệu ETFE-PEM 
có cấu trúc đa pha này có sự hiện diện của vùng chuyển tiếp của 2 
pha tinh thể và vô định hình, và sự thăng giáng của mật độ điện tử, 
do đó I(q) không thể tỷ lệ với q-4. Loại bỏ thăng giáng mật độ điện 
tử làm cho I(q) tỷ lệ với qn mà n tiến gần đến -4 (bảng 2) giúp cho 
việc xác định các cấu trúc khác được dễ dàng hơn. Hay nói cách 
khác, việc xác định bề dày vùng chuyển tiếp trong vùng q=0,6-2,5 
nm-1 chỉ có thể thực hiện sau khi loại bỏ đóng góp của I
Fl
(q). 
Hình 8. Cường độ SAXS trước (I(q)) và sau khi trừ thăng giáng 
mật độ điện tử (I(q) - IFl(q)) của mẫu ETFE ban đầu (A), ETFE-
PEM 19% (B), ETFE-PEM 34% (C) và ETFE-PEM 59% (D) 
trong vùng q=0,1-2,5 nm-1. 
Trang 9 
đổi từ tỷ lệ với q-3,5 sang q-3,92 trước và sau khi trừ IFl(q). Sự thay đổi mạnh mẽ của I(q) 
sau khi trừ IFl(q) trong vùng q=0,6-2,5 nm-1 cũng thu được đối với các mẫu còn lại. Theo 
quy luật Porod thì I(q) trong khu vực này cho vật liệu 2 pha hoàn hảo sẽ tỷ lệ với q-4 [14, 
15]. Tuy nhiên, trong vật liệu ETFE-PEM có cấu trúc đa pha này có sự hiện diện của 
vùng chuyển tiếp của 2 pha tinh thể và vô định hình, và sự thăng giáng của mật độ điện 
tử, do đó I(q) không thể tỷ lệ với q-4. Loại bỏ thăng giáng mật độ điện tử làm cho I(q) tỷ lệ 
với qn mà n tiến gần đến -4 (bảng 2) giúp cho việc xác định các cấu trúc khác được dễ 
dàng hơn. Hay nói cách khác, việc xác định bề dày vùng chuyển tiếp trong vùng q=0,6-
2,5 nm-1 chỉ có thể thực hiện sau khi loại bỏ đóng góp của IFl(q). 
10-1 100
10-1
100
101
102
103
(A)
q-3,32
 I(q)
 I(q) - IFL(q)
I(
q
) 
(c
m
-1
)
q (nm-1)
ETFE ban ñaàu
Ñænh Lamellar
q = 0,321 nm-1
d = 19,53 nm
q-2,59
10-1 100
10-1
100
101
102
103
(B)
 I(q)
 I(q) - IFL(q)
I(
q
) 
(c
m
-1
)
q (nm-1)
q-4,04
ETFE-PEM 19%
Ñænh Lamellar
q = 0,253 nm-1
d = 24,86 nm
q-3,85
10-1 100
10-1
100
101
102
103
(C)
 I(q)
 I(q) - IFL(q)
I(
q
) 
(c
m
-1
)
q (nm-1)
q-3,81
ETFE-PEM 34%
Ñænh Lamellar
q = 0,234 nm-1
d = 26,89 nm
q-3,51
10-1 100
10-1
100
101
102
103
(D)
q-3,92
I(
q
) 
(c
m
-1
)
q (nm-1)
 I(q)
 I(q) - IFL(q)
ETFE-PEM 59%
Ñænh Lamellar
q = 0,224 nm-1
d = 28,03 nm
q-3,51
Hình 8. Cường độ SAXS trước (I(q)) và sau khi trừ thăng giáng mật độ điện tử (I(q) 
- IFl(q)) của mẫu ETFE ban đầu (A), ETFE-PEM 19% (B), ETFE-PEM 34% (C) và 
ETFE-PEM 59% (D) trong vùng q=0,1-2,5 nm-1. 
Bảng 2. Hệ số góc của đường Porod khi tính bằng hàm log(q) và log(Iq) cho các mẫu 
ETFE-PEM có GD = 19%, 34% và 59% trước và sau khi trừ ảnh hưởng của Vonk 
bậc 6. 
Mẫu Trước khi trừ Vonk 6 Sau khi trừ Vonk 6 
ETFE ban đầu -2,59 0,04 -3,32 0,03 
ETFE-PEM 19% -3,85 0,04 -4,04 0,03 
ETFE-PEM 34% -3,52 0,03 -3,81 0,02 
ETFE-PEM 59% -3,51 0,04 -3,92 0,02 
 Hình 9 trình bày cường độ SAXS trước (9A1, 9B1, 9C1, 9D1) và sau khi trừ IFl(q) 
(9A2, 9B2, 9C2, 9D2) của các mẫu trong vùng q=2,5-10,5 nm-1. Trước khi trừ IFl(q), 
cường độ I(q) của mẫu ban đầu ETFE và ETFE-PEM 19% không có bất kỳ đỉnh tán xạ 
cực đại nào, trong khi các mẫu ETFE-PEM 34 và 59% xuất hiện đỉnh cực đại tại q≈4 nm-1 
tương ứng với kích thước tương quan d≈1,57 nm. Đỉnh cực đại này được quy cho cấu trúc 
của nhóm polystyrene sulfonic acid [6, 7]. Hình dạng các đỉnh SAXS cực đại tại q≈4 nm-1 
(hình 9C1, 9D1) phân bố rộng cho thấy các nhóm polystyrene sulfonic acid có trật tự và 
tương quan yếu. Ngoài ra, đỉnh cực đại SAXS có hình dạng không đối xứng, tức là chân 
bên trái thấp hơn trong khi chân bên phải của đỉnh cao hơn do nằm trên nền của cường độ 
tán xạ lớn do thăng giáng mật độ điện tử và pha vô định hình. Sự phân bố bị biến dạng 
này khiến cho việc phân tích và xử lý đỉnh (như làm khớp hình dạng đỉnh, tính diện tích 
5862(1) 1.2020
Khoa học Kỹ thuật và Công nghệ
Bảng 2. Hệ số góc của đường Porod khi tính bằng hàm log(q) và 
log(Iq) cho các mẫu ETFE-PEM có GD = 19%, 34% và 59% 
trước và sau khi trừ ảnh hưởng của Vonk bậc 6.
Mẫu Trước khi trừ Vonk 6 Sau khi trừ Vonk 6
ETFE ban đầu -2,59±0,04 -3,32±0,03
ETFE-PEM 19% -3,85±0,04 -4,04±0,03
ETFE-PEM 34% -3,52±0,03 -3,81±0,02
ETFE-PEM 59% -3,51±0,04 -3,92±0,02
Hình 9 trình bày cường độ SAXS trước (9A1, 9B1, 9C1, 9D1) 
và sau khi trừ I
Fl
(q) (9A2, 9B2, 9C2, 9D2) của các mẫu trong vùng 
q=2,5-10,5 nm-1. Trước khi trừ I
Fl
(q), cường độ I(q) của mẫu ban 
đầu ETFE và ETFE-PEM 19% không có bất kỳ đỉnh tán xạ cực 
đại nào, trong khi các mẫu ETFE-PEM 34 và 59% xuất hiện đỉnh 
cực đại tại q≈4 nm-1 tương ứng với kích thước tương quan d≈1,57 
nm. Đỉnh cực đại này được quy cho cấu trúc của nhóm polystyrene 
sulfonic acid [6, 7]. Hình dạng các đỉnh SAXS cực đại tại q≈4 
nm-1 (hình 9C1, 9D1) phân bố rộng cho thấy các nhóm polystyrene 
sulfonic acid có trật tự và tương quan yếu. Ngoài ra, đỉnh cực đại 
SAXS có hình dạng không đối xứng, tức là chân bên trái thấp hơn 
trong khi chân bên phải của đỉnh cao hơn do nằm trên nền của 
cường độ tán xạ lớn do thăng giáng mật độ điện tử và pha vô định 
hình. Sự phân bố bị biến dạng này khiến cho việc phân tích và xử 
lý đỉnh (như làm khớp hình dạng đỉnh, tính diện tích đỉnh và giá 
trị bề rộng tại một nửa chiều cao cực đại) trở nên khó khăn và kém 
chính xác. Sau khi loại trừ đóng góp của cường độ thăng giáng, 
hình dạng đỉnh đã trở nên cân bằng và nhọn hơn (hình 9C2, 9D2) 
nhưng vị trí đỉnh phổ không thay đổi. Ngoài ra, cường độ của đỉnh 
cực đại giảm đi rất nhiều (khoảng 95%) so với trước khi trừ I
Fl
(q). 
Kết quả trên cho thấy rằng, I
Fl
(q) ảnh hưởng đáng kể đến cường độ 
tán xạ tổng, hình dạng và phân bố đỉnh cực đại của I(q) tại vùng 
giá trị vector tán xạ góc lớn (q>2,5 cm-1).
Trang 10 
đỉnh và giá trị bề rộng tại một nửa chiều cao cực đại) trở nên khó khăn và kém chính xác. 
Sau khi loại trừ đóng góp của cường độ thăng giáng, hình dạng đỉnh đã trở nên cân bằng 
và nhọn hơn (hình 9C2, 9D2) nhưng vị trí đỉnh phổ không thay đổi. Ngoài ra, cường độ 
của đỉnh cực đại giảm đi rất nhiều (khoảng 95%) so với trước khi trừ IFl(q). Kết quả trên 
cho thấy rằng, IFl(q) ảnh hưởng đáng kể đến cường độ tán xạ tổng, hình dạng và phân bố 
đỉnh cực đại của I(q) tại vùng giá trị vector tán xạ góc lớn (q>2,5 cm-1). 
0,3
0,6
0,9
2,5 5,0 7,5 10,0
-0,05
0,00
0,05
0,10
I(
q
) 
(c
m
-1
)
Original ETFE
(A2)I(
q
)-
I F
L
(q
) 
(c
m
-1
)
q (nm-1)
(A1)
0,6
0,9
1,2
2,5 5,0 7,5 10,0
-0,05
0,00
0,05
0,10
I(
q
) 
(c
m
-1
)
ETFE-PEM 19%
I(
q
)-
I F
L
(q
) 
(c
m
-1
)
q (nm-1)
(B2)
(B1)
0,6
0,9
2,5 5,0 7,5 10,0
-0,05
0,00
0,05
0,10
q = 4,03 nm-1
I(
q
) 
(c
m
-1
)
ETFE-PEM 34%
(C2)
(C1)
d = 1,56 nm
I(
q
)-
I F
L
(q
) 
(c
m
-1
)
q (nm-1)
q = 4,03 nm-1
0,6
0,8
2,5 5,0 7,5 10,0
-0,05
0,00
0,05
0,10
I(
q
) 
(c
m
-1
)
ETFE-PEM 59%
(D2)
(D1)
d = 1,56 nm
q = 4,04 nm-1
q = 4,04 nm-1
I(
q
)-
I F
L
(q
) 
(c
m
-1
)
q (nm-1) 
Hình 9. Phổ thực nghiệm SAXS ban đầu (I(q)) và sau khi trừ thăng giáng tính theo 
Vonk 6 (I(q)–IFl(q)) của các mẫu: ETFE ban đầu (A), ETFE-PEM 19% (B), ETFE-
PEM 34% (C) và ETFE-PEM 59% (D). 
Kết luận 
Việc khảo sát các hàm Vonk có bậc khác nhau dựa trên thông số H (sự đóng góp của 
thăng giáng mật độ điện tử đến cường độ tán xạ tổng) cho thấy, hàm Vonk bậc 6 là phù 
hợp nhất để tính toán và đánh giá thăng giáng mật độ điện tử cho các mẫu màng dẫn 
proton ETFE-PEM. Kết quả cho thấy rằng, thăng giáng mật độ điện tử ảnh hưởng mạnh 
mẽ đến cấu trúc bề dày vùng chuyển tiếp và cấu trúc vùng dẫn ion nhưng không đáng kể 
đối với cấu trúc lamellar. Ngoài ra, việc tính toán cấu trúc vùng chuyển tiếp chỉ có thể 
thực hiện sau khi trừ thăng giáng điện tử. Các giá trị thăng giáng mật độ điện tử Fl thay 
đổi theo mức độ ghép mạch bức xạ và theo quy trình tổng hợp mẫu. Việc loại bỏ thăng 
giáng mật độ điện tử đã làm rõ các đỉnh cấu trúc trong khu vực vector tán xạ góc lớn, giúp 
phân tích các đỉnh cấu trúc tại vùng này được chính xác hơn. Các nghiên cứu tiếp theo để 
tính toán định lượng giá trị bề dày vùng chuyển tiếp và mối liên hệ của chúng với độ bền 
cơ lý và mức độ phân tách pha sẽ được thực hiện. 
TÀI LIỆU THAM KHẢO 
[1] B. Smitha, S. Sridhar, A.A. Khan (2005), “Solid polymer electrolyte membranes 
for fuel cell applications - A review”, Journal of Membrane Science, 259, pp.10-26. 
[2] D. Brandell, J. Karo, A. Liivat, J.O. Thomas (2007), “Molecular dynamics 
studies of the nafion, dow and aciplex fuel-cell polymer membrane systems”, Journal of 
Molecular Modeling, 13, pp.1039-1046. 
[3] A. Baroutaji, J.G. Carton, M. Sajjia, A.G. Olabi (2016), “Materials in ETFE-
PEM fuel cells”, Reference Module in Materials Science and Materials Engineering. 
Hình hổ thực nghiệm SAXS ban đầu (I(q)) và sau khi trừ thăng 
giáng tính theo Vonk 6 (I(q) - IFl(q)) của các mẫu: ETFE ban đầu 
(A), ETFE-PEM 19% (B), ETFE-PEM 34% (C) và ETFE-PEM 
59% (D).
Kết luận
Việc khảo sát các hàm Vonk có bậc khác nhau dựa trên thông số 
H (sự đóng góp của thăng giáng mật độ điện tử đến cường độ tán xạ 
tổng) cho thấy, hàm Vonk bậc 6 là p ù hợp nhất ể tí h toán và đánh 
giá thă g giáng mật độ điện tử cho các mẫu màng dẫ proton ETFE-
PEM. Kết quả cho thấy rằng, thăng giá g mật độ điện tử ảnh hưởng 
mạnh mẽ đến cấu trúc bề dày vùng chuyển tiếp và cấu trúc vùng dẫn 
ion nhưng không đáng kể đối với cấu trúc lamellar. Ngoài ra, việc tính 
toán cấu trúc vùng chuyển tiếp chỉ có thể thực hiện sau khi trừ thăng 
giáng điện tử. Các giá trị thăng giáng mật độ điện tử Fl thay đổi theo 
mức độ ghép mạch bức xạ và theo quy trình tổng hợp mẫu. Việc loại 
bỏ thăng giáng mật độ điện tử đã làm rõ các đỉnh cấu trúc trong khu 
vực vector tán xạ góc lớn, giúp phân tích các đỉnh cấu trúc tại vùng 
này được chính xác hơn. Các nghiên cứu tiếp theo để tính toán định 
lượng giá trị bề dày vùng chuyển tiếp và mối liên hệ của chúng với độ 
bền cơ lý và mức độ phân tách pha sẽ được thực hiện. 
TÀI LIỆU THAM KHẢO
[1] B. Smitha, S. Sridhar, A.A. Khan (2005), “Solid polymer electrolyte membranes 
for fuel cell applications - A review”, Journal of Membrane Science, 259, pp.10-26.
[2] D. Brandell, J. Karo, A. Liivat, J.O. Thomas (2007), “Molecular dynamics 
studies of the nafion, dow and aciplex fuel-cell polymer membrane systems”, Journal 
of Molecular Modeling, 13, pp.1039-1046.
[3] A. Baroutaji, J.G. Carton, M. Sajjia, A.G. Olabi (2016), “Materials in ETFE-
PEM fuel cells”, Reference Module in Materials Science and Materials Engineering.
[4] N.L. Garland, T.G. Benjamin, J.P. Kopasz (2008), “Materials tssues in polymer 
electrolyte membrane fuel cells”, Material Matters, 34, pp.85.
[5] D. Sebastian, V. Baglio (2017), “Advanced materials in polymer electrolyte 
fuel cells”, Materials, 10, pp.1163-1166.
[6] T.D. Tap, S. Sawada, S. Hasegawa, K. Yoshimura, Y. Oba, M. Ohnuma, Y. 
Katsumura, Y. Maekawa (2014), “Hierarchical structure-property relationships in graft-
type fluorinated polymer electrolyte membranes using small- and ultrasmall-angle 
X-ray scattering analysis”, Macromolecules, 47, pp.2373-2383.
[7] T.D. Tap, S. Sawada, S. Hasegawa, Y. Katsumura, and Y. Maekawa (2013), 
“Poly(ethylene-co-tetrafluoroethylene) (ETFE)-based graft-type polymer electrolyte 
membranes with different ion exchange capacities: relative humidity dependence for 
fuel cell applications”, Journal of Membrane Science, 447, pp.19-25. 
[8] T.D. Tap, D.D. Khiem, L.L. Nguyen, N.Q. Hien, L.Q. Luan, P.B. Thang, S. 
Sawada, S. Hasegawa, Y. Maekawa (2018), “Humidity and temperature effects on 
mechanical properties and conductivity of graft-type polymer electrolyte membrane”, 
Radiation Physics and Chemistry, 151, pp.186-191.
[9] T.D. Tap, P.M. Hien, N.H. Anh, L.T. Anh, L.A. Tuyen (2015), “Study of 
lamellar structures of graft-type fluorinated proton exchange membranes by small-
angle X-ray scattering: preparation procedures and grafting degree dependence for fuel 
application”, Science & Technology Development Journal, 8, pp.153-161.
[10] N. Stribeck (2007), X-ray Scattering of Soft Matter, Springer, pp.118-119.
[11] R. Bonart, E.H. Mȕller (1974), “Phase separation in urethane elastomers as 
judged by low-angle X-ray scattering. I. Fundamentals”, Journal of Macromolecular 
Science, Part B: Physics, 10, pp.177-189.
[12] W. Ruland (1971), “Small-angle scattering of two-phase systems: 
determination and significance of systematic deviations from porod’s law”, Journal of 
Applied Crystallography, 4, pp.70-77.
[13] C.G. Vonk (1973), “Investigation of non-ideal two-phase polymer structures 
by small-angle X-ray scattering”, Journal of Applied Crystallography, 6, pp.81-86.
[14] G. Porod (1951), “Die röntgenkleinwinkelstreuung von dichtgepackten 
kolloiden systemen”, Kolloid-Z, 124, pp.83-114.
[15] M.H. Kim (2004), “Modified porod’s law estimate of the transition-layer 
thickness between two phases: test of triangular smoothing function”, Journal of 
Applied Physics, 37, pp.643-651.