Ứng dụng lý thuyết giao nhau điểm yên ngựa xác định vị trí đặt svc nhằm nâng cao ổn định điện áp

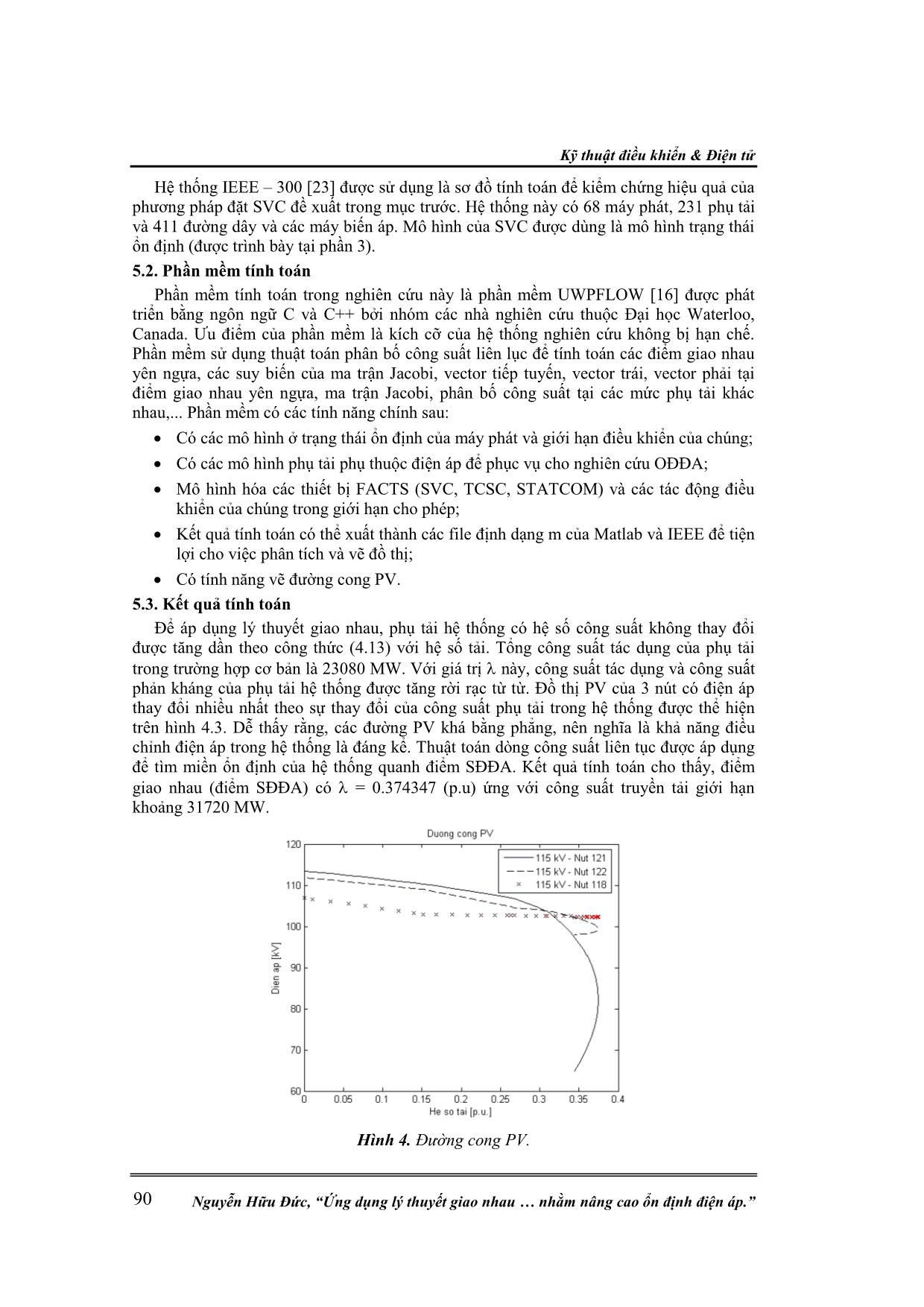
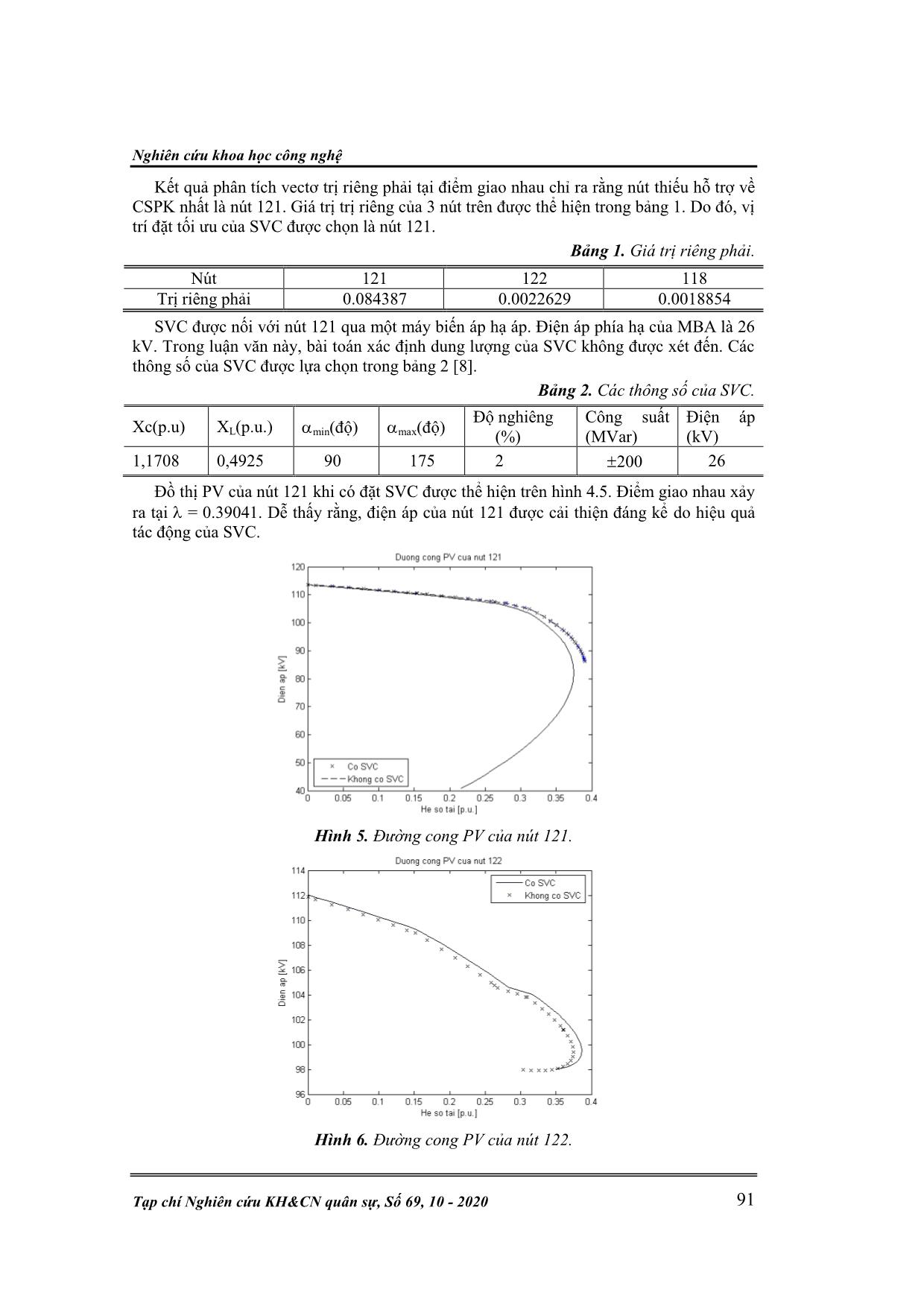
 các suy biến dương i sao cho 1 2 . . . n. 
Phương trình (12) thường được dùng để xác định hạng của ma trận (số lượng các giá trị 
suy biến của J khác 0). 
Do ma trận Jacobian có đạo hàm bậc một của các phương trình cân bằng công suất 
phản kháng Q(z, ) theo điện áp V z, nên tuyến tính hóa phương trình F(z, ) = 0 tại 
điểm cân bằng (z0, 0), ta có: 
( , )F z J z  
0 0 0 0
0 0 0 0
ˆ ˆ
( , ) ( , )ˆ ˆˆ( , , ) ˆ
ˆ( , , )
( , ) ( , )
ˆ
F F
z z
zF z V z V
VQ z V Q Q
z z
z V
  
 
 
  
   
  
   
=
1 2
3 4
ˆJ J z
J J V
(13) 
Trong đó: 
- ˆ ( , )F z  là độ lệch công suất tác dụng P(z, ); 
- z là góc . 
Phương trình (13) được biến đổi thành phương trình sau: 
1
1
ˆˆ ˆ( , , )
ˆ( , , )
n
T
i i i
i
z F z V
s r
V Q z V
 

 
 (14) 
Cần chú ý rằng, giá trị suy biến nhỏ nhất là đại lượng cho biết hệ thống gần điểm 
SĐĐA (hay điểm suy biến) thế nào. Hơn nữa, vì n 0 khi hệ thống lân cận điểm SĐĐA, 
nên phương trình (14) được viết lại như sau: 
1
ˆˆ ˆ( , , )
ˆ( , , )
T
i i i
z F z V
s r
V Q z V
 

 
 (15) 
Có thể thấy rằng, vectơ suy biến phải sn phản ánh thông tin hữu ích về OĐĐA. Các giá 
trị lớn nhất của sn chỉ ra các thanh cái nhạy cảm nhất về điện áp trong hệ thống (các thanh 
cái nguy hiểm). Các giá trị lớn nhất của rn ứng với các thanh cái trong hệ thống nhạy cảm 
nhất về công suất tác dụng. 
Giả thiết rằng ˆ ˆ( , , ) 0F z V  , thì phương trình (15) có dạng: 
1
4 3 1 2
ˆ( , , ) ( )Q z V J J J J V  (16) 
= JQV V 
Nói chung, tại điểm SĐĐA ma trận J suy biến nhưng J1 không suy biến. Do đó, ma trận 
JQV trở nên suy biến tại điểm SĐĐAP vì: 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số 69, 10 - 2020 89 
1
det
det
det
QV
J
J
J
 (17) 
Các giá trị suy biến của ma trận rút gọn này được dùng để xác định lân cận điểm SĐĐA. 
4.2.2. Phân tích vectơ trị riêng 
Xét ma trận vuông n x n Jacobi J = DzF(z0, 0) tại điểm cân bằng (z0, 0), ta có: 
1
n
T T
i i i
i
J WAU v 
  (18) 
Trong đó: 
- W là ma trận phức các vector trị riêng phải i; 
- U là ma trận phức các vectơ trị riêng trái vi; 
- A là ma trận đường chéo của các trị riêng i. 
Phân tích tương tự như với trường hợp giá trị suy biến, ta cũng có chung kết luận. Các 
giá trị lớn nhất của i phản ánh các thanh cái nhạy cảm nhất về điện áp trong hệ thống. 
Các giá trị lớn nhất của vi cho biết các thanh cái trong hệ thống nhạy cảm nhất về công 
suất tác dụng. 
Như đã trình bày trong phần 2, trên quỹ đạo nghiệm của hệ phương trình phân bố công 
suất, các nghiệm ổn định và không ổn định tiến lại gần nhau và gặp nhau tại điểm giao 
nhau yên ngựa khi phụ tải tăng. Điểm giao nhau gây mất OĐĐA này còn là giới hạn công 
suất truyền tải. Trên cơ sở phân tích trị riêng của ma trận Jacobi tại điểm giao nhau, vectơ 
trị riêng phải cho biết thanh cái nào trong hệ thống đóng góp nhiều nhất dẫn đến SĐĐA. 
Do đó, thanh cái có giá trị riêng phải lớn nhất sẽ được lựa chọn để đặt SVC. 
5. MÔ PHỎNG VÀ THẢO LUẬN 
5.1. Hệ thống điện mô phỏng 
Hình 3. Sơ đồ hệ thống 300 nút của IEEE [23]. 
Kỹ thuật điều khiển & Điện tử 
Nguyễn Hữu Đức, “Ứng dụng lý thuyết giao nhau  nhằm nâng cao ổn định điện áp.” 90 
Hệ thống IEEE – 300 [23] được sử dụng là sơ đồ tính toán để kiểm chứng hiệu quả của 
phương pháp đặt SVC đề xuất trong mục trước. Hệ thống này có 68 máy phát, 231 phụ tải 
và 411 đường dây và các máy biến áp. Mô hình của SVC được dùng là mô hình trạng thái 
ổn định (được trình bày tại phần 3). 
5.2. Phần mềm tính toán 
Phần mềm tính toán trong nghiên cứu này là phần mềm UWPFLOW [16] được phát 
triển bằng ngôn ngữ C và C++ bởi nhóm các nhà nghiên cứu thuộc Đại học Waterloo, 
Canada. Ưu điểm của phần mềm là kích cỡ của hệ thống nghiên cứu không bị hạn chế. 
Phần mềm sử dụng thuật toán phân bố công suất liên lục để tính toán các điểm giao nhau 
yên ngựa, các suy biến của ma trận Jacobi, vector tiếp tuyến, vector trái, vector phải tại 
điểm giao nhau yên ngựa, ma trận Jacobi, phân bố công suất tại các mức phụ tải khác 
nhau,... Phần mềm có các tính năng chính sau: 
 Có các mô hình ở trạng thái ổn định của máy phát và giới hạn điều khiển của chúng; 
 Có các mô hình phụ tải phụ thuộc điện áp để phục vụ cho nghiên cứu OĐĐA; 
 Mô hình hóa các thiết bị FACTS (SVC, TCSC, STATCOM) và các tác động điều 
khiển của chúng trong giới hạn cho phép; 
 Kết quả tính toán có thể xuất thành các file định dạng m của Matlab và IEEE để tiện 
lợi cho việc phân tích và vẽ đồ thị; 
 Có tính năng vẽ đường cong PV. 
5.3. Kết quả tính toán 
Để áp dụng lý thuyết giao nhau, phụ tải hệ thống có hệ số công suất không thay đổi 
được tăng dần theo công thức (4.13) với hệ số tải. Tổng công suất tác dụng của phụ tải 
trong trường hợp cơ bản là 23080 MW. Với giá trị  này, công suất tác dụng và công suất 
phản kháng của phụ tải hệ thống được tăng rời rạc từ từ. Đồ thị PV của 3 nút có điện áp 
thay đổi nhiều nhất theo sự thay đổi của công suất phụ tải trong hệ thống được thể hiện 
trên hình 4.3. Dễ thấy rằng, các đường PV khá bằng phẳng, nên nghĩa là khả năng điều 
chỉnh điện áp trong hệ thống là đáng kể. Thuật toán dòng công suất liên tục được áp dụng 
để tìm miền ổn định của hệ thống quanh điểm SĐĐA. Kết quả tính toán cho thấy, điểm 
giao nhau (điểm SĐĐA) có  = 0.374347 (p.u) ứng với công suất truyền tải giới hạn 
khoảng 31720 MW. 
Hình 4. Đường cong PV. 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số 69, 10 - 2020 91 
Kết quả phân tích vectơ trị riêng phải tại điểm giao nhau chỉ ra rằng nút thiếu hỗ trợ về 
CSPK nhất là nút 121. Giá trị trị riêng của 3 nút trên được thể hiện trong bảng 1. Do đó, vị 
trí đặt tối ưu của SVC được chọn là nút 121. 
Bảng 1. Giá trị riêng phải. 
Nút 121 122 118 
Trị riêng phải 0.084387 0.0022629 0.0018854 
SVC được nối với nút 121 qua một máy biến áp hạ áp. Điện áp phía hạ của MBA là 26 
kV. Trong luận văn này, bài toán xác định dung lượng của SVC không được xét đến. Các 
thông số của SVC được lựa chọn trong bảng 2 [8]. 
Bảng 2. Các thông số của SVC. 
Xc(p.u) XL(p.u.) min(độ) max(độ) 
Độ nghiêng 
(%) 
Công suất 
(MVar) 
Điện áp 
(kV) 
1,1708 0,4925 90 175 2 200 26 
Đồ thị PV của nút 121 khi có đặt SVC được thể hiện trên hình 4.5. Điểm giao nhau xảy 
ra tại  = 0.39041. Dễ thấy rằng, điện áp của nút 121 được cải thiện đáng kể do hiệu quả 
tác động của SVC. 
Hình 5. Đường cong PV của nút 121. 
Hình 6. Đường cong PV của nút 122. 
Kỹ thuật điều khiển & Điện tử 
Nguyễn Hữu Đức, “Ứng dụng lý thuyết giao nhau  nhằm nâng cao ổn định điện áp.” 92 
Kết quả tính toán của trường hợp nút 121 có SVC chỉ ra rằng, tổng công suất tác dụng 
của hệ thống tại điểm SĐĐA là 32091 MW ( = 0.39041), tăng thêm 1,6% tổng công suất 
tác dụng của trường hợp cơ bản. So với trường hợp không đặt SVC, hệ thống có khả năng 
truyền tải thêm một lượng công suất là 370 MW khi đặt SVC tại nút 121. 
Để chỉ ra hiệu quả của vị trí đặt SVC được lựa chọn, giới hạn công suất truyền tải của 
hệ thống được tính với các trường hợp SVC đặt tại nút 118 và 122. Giá trị  (p.u.) của các 
trường hợp này được trình bày trong bảng 3. Bảng 4 thể hiện các giá trị công suất truyền 
tải lớn nhất của hệ thống trong các trường hợp đặt SVC tại các nút khác nhau. 
Bảng 3. So sánh ảnh hưởng của các vị trí đặt SVC tới . 
 Không có SVC 
Có SVC 
121 122 118 
 (p.u) 0.374347 0.39041 0.386279 0.386023 
Hình 7. Đường cong PV của nút 118. 
Bảng 4. So sánh công suất truyền tải giới hạn. 
 Không có SVC 
Có SVC 
121 122 118 
P (MW) 31720 32090 31995 31975 
Bảng 5. Lượng công suất truyền tải tăng thêm khi có SVC. 
Có SVC 
121 122 118 
P (MW) 370 275 232 
Từ bảng 4 – bảng 5, ta thấy rằng đặt SVC vào nút 121 thì giới hạn công suất truyền tải 
được cải thiện nhất. Dễ thấy rằng, thì giới hạn công suất truyền tải giảm đi 0,41% nếu 
cũng dùng SVC đó tại nút 122. Tương tự, nếu đặt SVC ở nút 118, thì giới hạn công suất 
truyền tải bị giảm lên đến 0.59%. Tóm lại, nút 121 là nút tối ưu để đặt SVC vì giới hạn 
công suất truyền tải được nâng cao nhất và điện áp của nút cũng bằng phẳng hơn. 
4. KẾT LUẬN 
SĐĐA là một sự cố nghiêm trọng trong HTĐ. Với lý thuyết giao nhau tại điểm yên 
ngựa, hiện tượng này hoàn toàn được giải thích rõ ràng. Trên cơ sở đó, nghiên cứu đã ứng 
dụng lý thuyết giao nhau tại điểm yên ngựa vào xác định thanh cái dễ mất OĐĐA nhất để 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số 69, 10 - 2020 93 
tiến hành đặt thiết bị SVC nhằm nâng cao mức OĐĐA tĩnh. Phương pháp trình bày trong 
nghiên cứu hiệu quả trong bài toán xác định vị trí tối ưu của SVC để nâng cao ổn định của 
hệ thống. Tiếp tục mở rộng hướng nghiên cứu này, nhóm tác giả sẽ đưa bài toán tìm vị trí 
đặt SVC kết hợp xác định dung lượng và số lượng tối ưu đặt SVC trong hệ thống điện. 
Ngoài ra, một hướng nghiên cứu nữa là phân tích, so sánh hiệu quả nâng cao OĐĐA cả về 
kinh tế và kỹ thuật của một số thiết bị FACTS như SVC, TCSC và STATCOM trong bài 
toán nâng cao OĐĐA của hệ thống điện. 
TÀI LIỆU THAM KHẢO 
[1]. A. Monticelli, M.V.F Pereia and S. Granville, “Security constrained optimal power 
flow with post-contingency corrective rescheduling”, IEEE Trans. On Power 
Systems, Vol. PWRS-2, No.2,pp, 175-182, February 1987. 
[2]. A. Nanda and M.L. Crow, “An energy based approach to undervoltage load 
shedding”, Electric Power Systems Research, Vol. 32, pp. 11-18,1995. 
[3]. R.C. Burchett and H.H.Happ, “Large scale security dispatching: An exact model”, 
IEEE Trans. On Power Systems, Vol. PAS -102, No.9, pp. 2995 -2999, 9/1983. 
[4]. S. Granville, “Optimal reactive power dispatch through interior point methods”, 
IEEE Trans. On Power System, Vol. 9, No. 1, pp 136-146, 2/1994. 
[5]. N. G. Hingorani and L. Gyugyi, “Understanding FACTS: Concepts and Technology 
of Flexible AC Transmission System”, IEEE Press, 2000. 
[6]. B. Vardani, “Optimimum Location of SVC in an IEEE 33 Bus Radial Distribution 
System Using Power Sensitivity Index”, 2019 Internation Conf. on Electrical, 
Electronics and Computer Engineering (UPCON), India, Nov. 2019. 
[7]. M. P. Babu; B. R. Lakshmikantha; and K. S. Sundar, “A Novel Method for 
Assessment of Voltage Stabitlity Improvement of Radian Distribution System Using 
SVC at Optimal Location”, 2018 International Conf. on Electrical, Electronics, 
Comunication, Computer, and Optimization Techniques, 2018. 
[8]. Sebastian Wildenhues, Jose L. Rueda and Istvan Erlich, "Optimal Allocation and 
Sizing of Dynamic Var Sources Using Heuristic Optimization", IEEE Transaction on 
power system, vol. 30, no. 5, September 2015. 
[9]. Pooja P. Kulkarni and N.D. Ghawghawe, "Optimal Placement and parameter setting 
of TCSC in Power Transmission System to increase the Power Transfer 
Capability", International Conference on Energy Systems and Applications (ICESA-
2015). 
[10]. Kabir Chakraborty, Gagari Deb and Sumita Deb, "Voltage Stability Assessment in 
Radial Distribution System by Line Stability Indicator (LSI) and its Improvement 
using SVC", 1st IEEE International Conference on Power Electronics. Intelligent 
Control and Energy Systems, 2016. 
[11]. Nikhlesh Kumar Sharma, Arindam Ghosh, Rajiv Kumar Varma, “A novel placement 
strategy for FACTS controllers”, IEEE Trans. On Power Delivery, Vol. 18,No.3, pp. 
982-987, July 2003. 
[12]. M. J.Laufenberg, M.A. Pai and K.R. Padiyar, “Hopf bifurcation control in power 
systems with static Var compensators”, International Journal of Electrical Power and 
Energy Systems, Vol. 19, No. 5, pp. 339-347, 1997. 
[13]. Naoto Yorino, E. E. El- Araby, Hiroshi Sasaki, Shigemi Harada, “A new formulation 
for FACTS allocation for security enhancement against voltage collapse”, IEEE 
Trans. On power systems, Vol. 18, No. 1, pp 3-10,2/2003. 
[14]. Hal Feng Wang, H. Li, H. chen, “Coordinated secondary voltage control to 
eliminate violations in power system contingencies”, IEEE Trans. On Power 
Systems, Vol.18, No. 2, pp. 588-595, May 2003. 
Kỹ thuật điều khiển & Điện tử 
Nguyễn Hữu Đức, “Ứng dụng lý thuyết giao nhau  nhằm nâng cao ổn định điện áp.” 94 
[15]. V. Ajjarapu and C. Christy, “The continuation Power Flow: A tool for steady state 
voltage stability analysis”, IEEE Trans. On Power systems, Vol. 7, No.1,pp. 416-
423, 2/1992. 
[16]. “UWPFLOW software: “Continuation and Direct Methods to locate Fold 
Bifurcations in AC/DC/ FACTS Power Sytems” by Claudio A. Canizares and 
Fernando L. Alvarado. 
[17]. CIGRE WG 38.02 Task Force No 10, "Modeling of voltage collapse including 
dynamic phenomena" technical report of task force 38-02-10, draft 3, CIGRE, June 
1992. 
[18]. R.B. Prada, B.j. Cory and R. Navarro Perez, "Assessment of steady state voltage 
collapse" Proc. of the Tenth Power Systems Computation Conference, Graz, 
Austria, August 1990, pp. 1599 - 1195. 
[19]. V, Ajjarapu, "Identification of steady state voltage stability in power system" Proc. 
of International Conference on High Technology in the Power Industry, March 
1988, pp. 244 – 247. 
[20]. C. A. Canizares and F. L. Alvarado, “Point of Collapse and continuation Methods 
for Large AC/DC Systems,” IEEE Trans. Power Systems, Vol. *, No.1, February 
1993, ph-¬ng ph¸p.1-8. 
[21]. C. A. Canizares, F. l. Alvarado, C. L. DeMarco, I. Dobson and W. F. Long, “Point 
of Collapse Methods Applied to AC/DC Power Systems,”, IEEE Trans. Power 
Systems, Vol. 7, No.2, May 1992, p.p. 673-683. 
[22]. J. Arrillaga and C.P. Arnold, Computer Analysis of Power Systems, John Wiley, 1990. 
[23]. Mike Adibi, “The IEEE 300 bus test case,” developed by IEEE Test Systems Task 
Force in 1993. 
ABSTRACT 
A METHOD BASED ON THE SADDLE NODE BIFURCATION TO DETERMINE AN 
OPTIMAL LOCATION OF SVC FOR IMPROVEMENT OF VOLTAGE STABILITY 
OF THE ELECTRICAL POWER SYSTEM 
 The phenomenon of voltage instability and voltage collapse in the power system 
are particularly severe problems. Many publications analyze and evaluate the 
phenomena of voltage disturbance, voltage stability, and solutions to improve the 
power system's voltage stability. In particular, the solution for applying the SVC 
equipment (Static Var Compensator) to help improve voltage stability has proven 
effective. However, due to the high cost of the SVC equipment, determining the SVC 
location to improve the best voltage is essential, especially for the Vietnamese 
power system. In this paper, the method of applying the saddle point intersection 
theory to determine SVC's optimal location to help improve the system voltage was 
presented. The simulation results were performed on UPFLOW software with a test 
case of the IEEE-300 bus test system. 
Keywords: Voltage stability; Voltage collapse; SVC; UPFLOW. 
Nhận bài ngày 27 tháng 8 năm 2020 
Hoàn thiện ngày 08 tháng 10 năm 2020 
Chấp nhận đăng ngày 15 tháng 10 năm 2020 
Địa chỉ: Khoa Công nghệ Năng lượng/Trường Đại học Điện lực. 
*Email: ducnh@epu.edu.vn.