Ứng dụng bộ lọc kalman trong rơle bảo vệ khoảng cách sử dụng đặc tuyến khởi động MHO

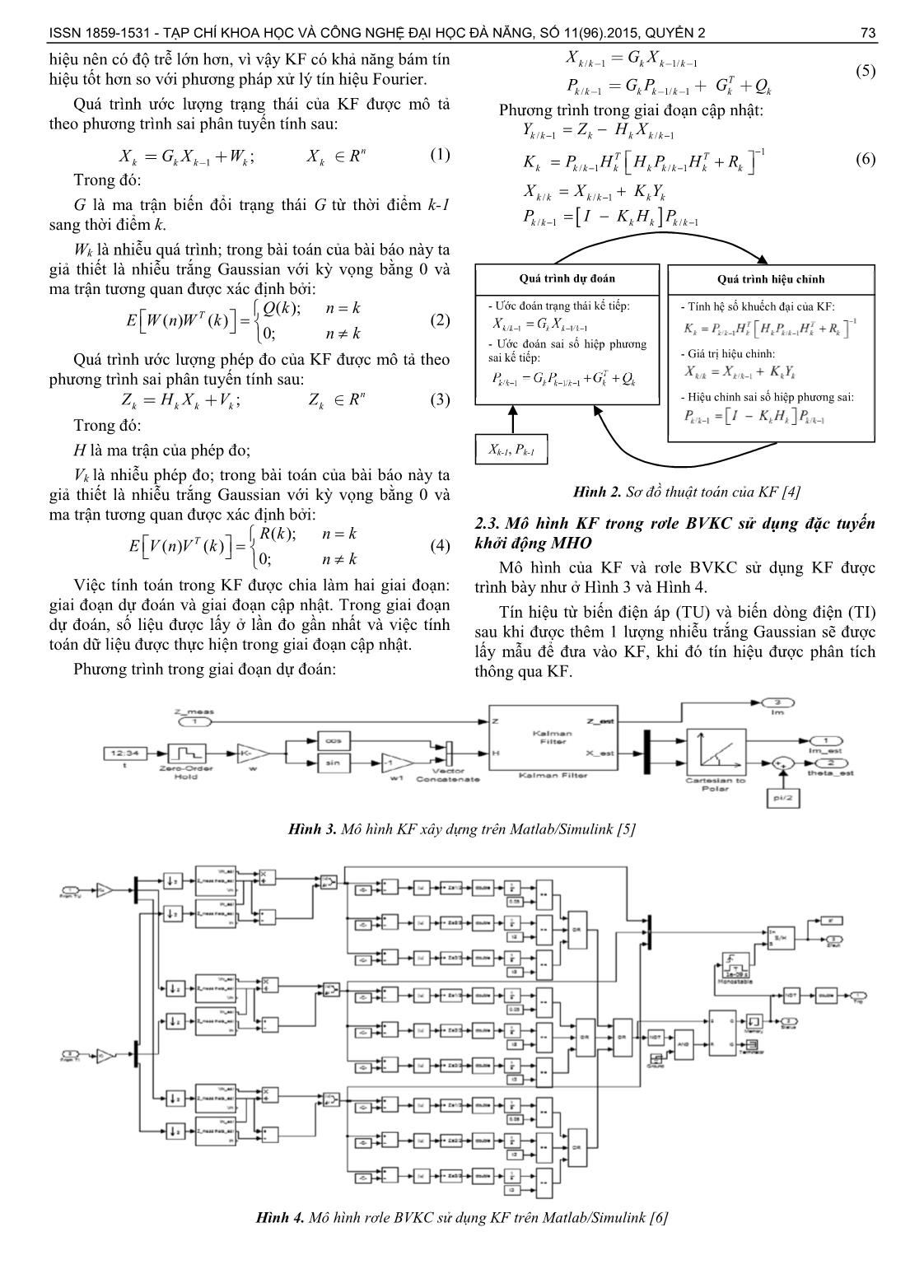
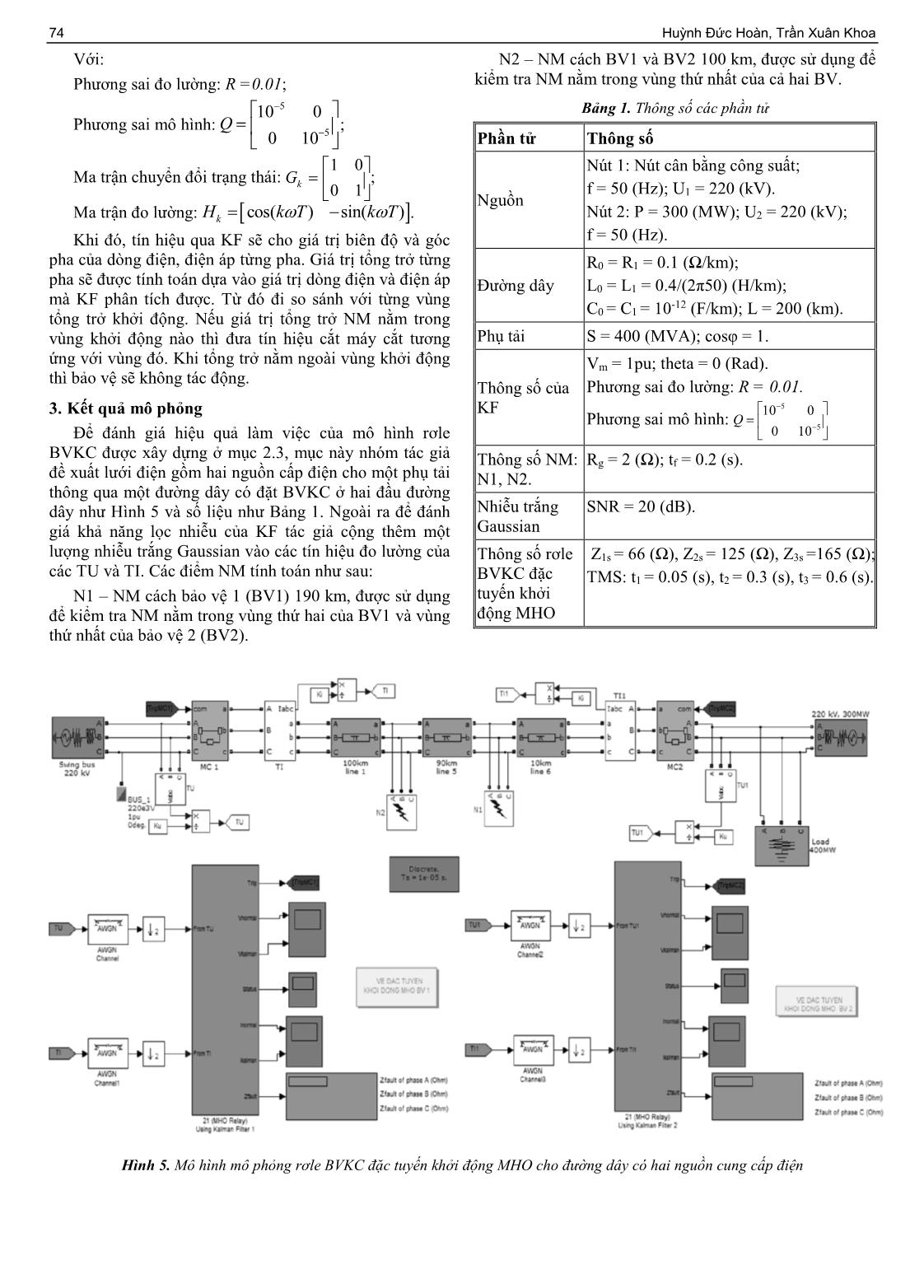
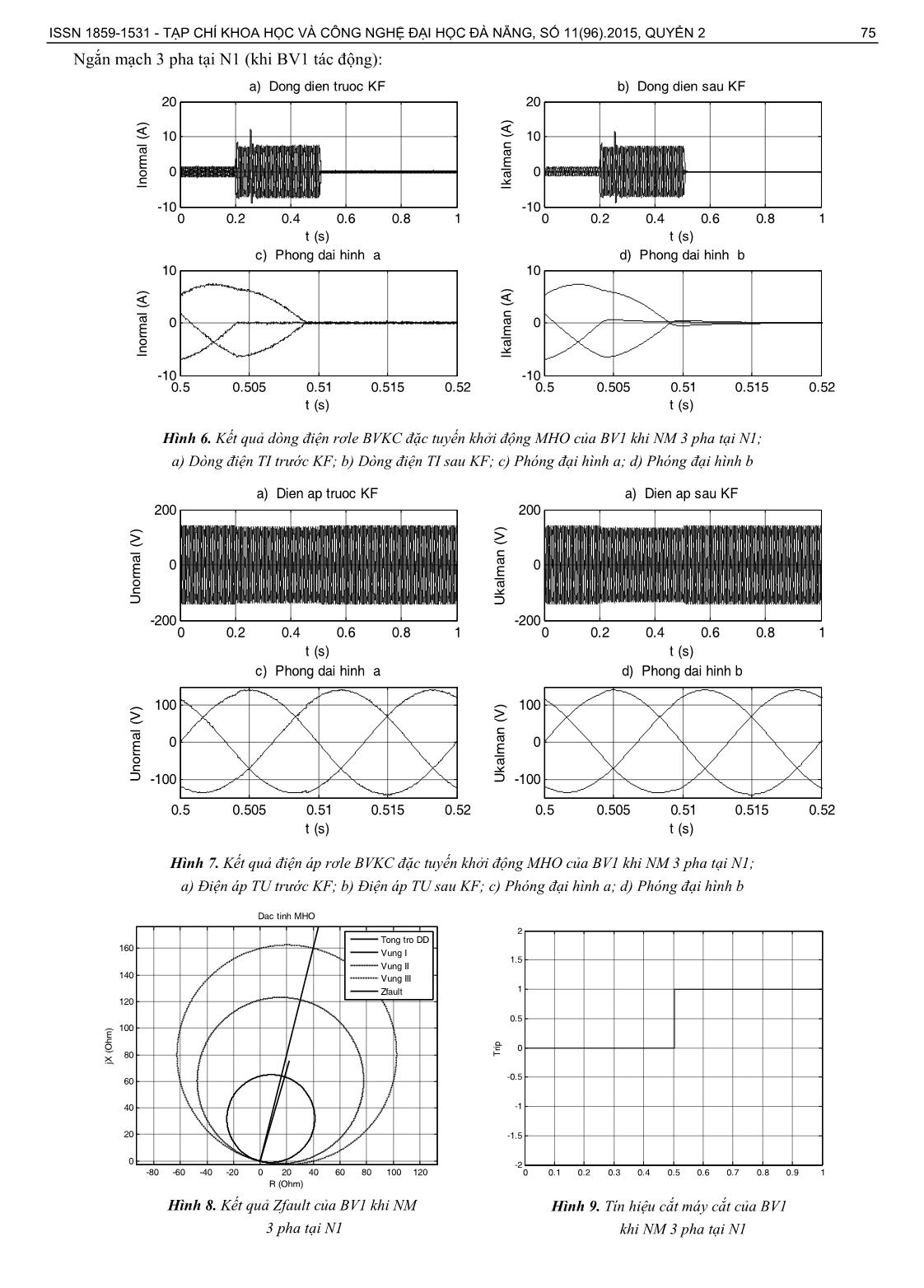
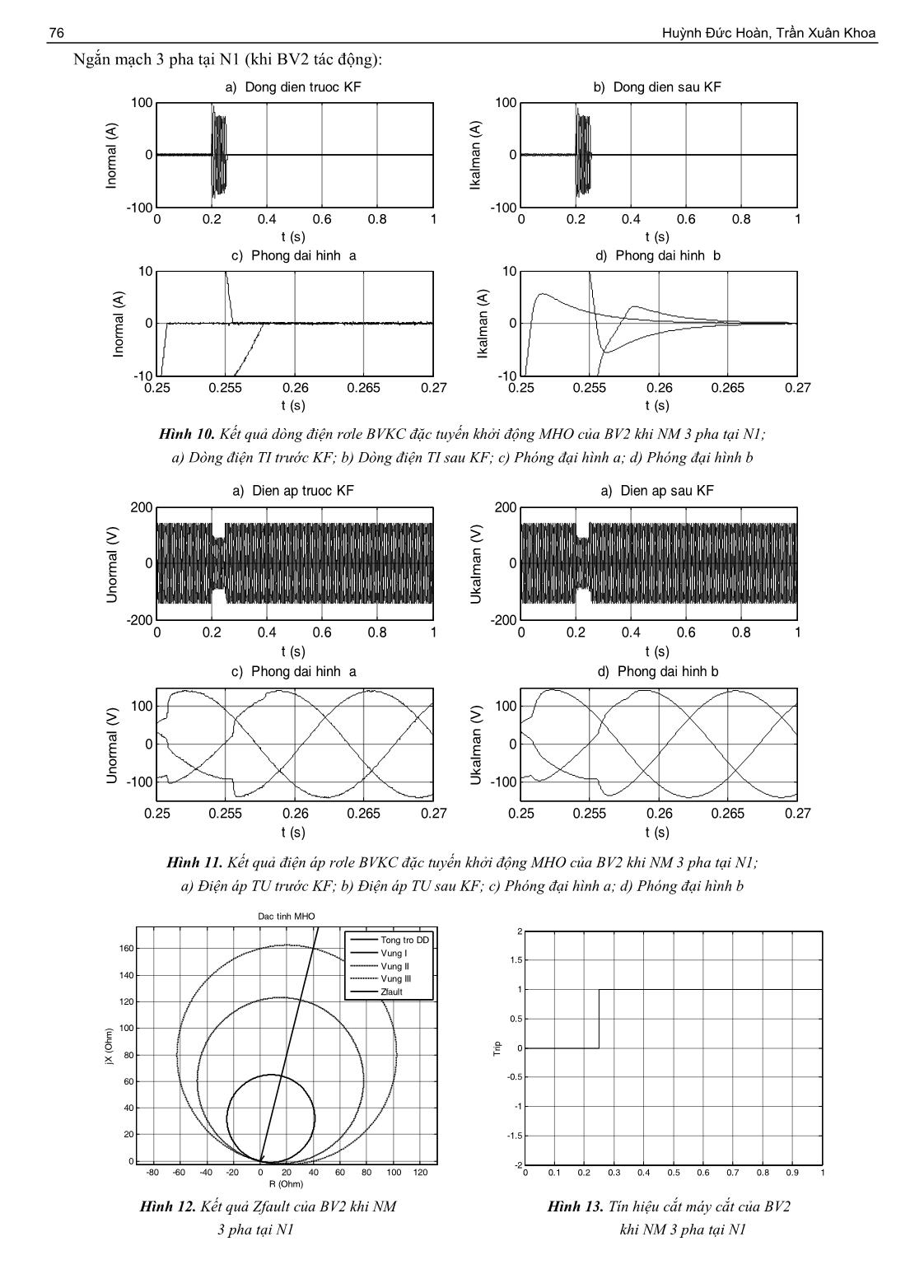
e 
breaker with the corresponding setting time. This paper proposes 
a line model with two sources and a load in Matlab/Simulink to 
evaluate the effectiveness of the proposed algorithm. The 
simulation results show that the proposed algorithm works
correctly and increase the reliability of protection relay. 
Từ khóa - bộ lọc Kalman; bảo vệ khoảng cách; đặc tuyến MHO;
Matlab/Simulink; rơle. 
 Key words - Kalman filter; distance protection; MHO 
characteristic; Matlab/Simulink; relay. 
1. Đặt vấn đề 
Việc yêu  cầu  nâng  cao  độ  tin  cậy  của  hệ  thống  điện 
cũng như độ tin cậy của bảo vệ rơle ngày càng được quan 
tâm,  nhưng  trong  quá  trình  đo  lường  hay  truyền  tải  tín 
hiệu của bảo vệ rơle thường gây ra nhiễu và sai số trong 
đo  lường, điều này sẽ  làm giảm độ  tin cậy của hệ  thống 
bảo vệ rơle. Nên việc xử lý tín hiệu để giảm lượng nhiễu 
và  nâng  cao  độ  chính  xác  trong  đo  lường  của  hệ  thống 
bảo  vệ  rơle  là  một  vấn  đề  rất  cần  thiết.  Việc  xử  lý  tín 
hiệu  trong bảo vệ  rơle  yêu cầu độ chính xác cao nhằm 
tránh hiện tượng tác động nhầm sự cố do nhiễu hay sai 
số trong quá trình đo lường gây ra, gây thiệt hại cho hệ 
thống  điện.  Vì  vậy,  việc  tìm  ra  những  phương  pháp 
nâng cao độ chính xác  trong xử  lý  tín hiệu  của bảo vệ 
rơle  nhằm  nâng  cao  độ  tin  cậy  cung  cấp  điện  là  một 
điều cần thiết. 
Hiện nay, việc xử lý tín hiệu trong hệ thống điện chủ 
yếu  dùng  phép  biến  đổi  Fourier,  nhưng  phép  biến  đổi 
Fourier  có  một  số  nhược  điểm,  đó  là  khi biến đổi  sang 
miền  tần  số,  thông  tin  thời  gian  đã  bị  mất,  nên  dựa  vào 
biến đổi Fourier của  tín hiệu  ta sẽ không  thể nào biết cụ 
thể thời gian diễn ra sự kiện. Nếu một thuộc tính tín hiệu 
không  thay đổi nhiều  theo  thời gian, còn được gọi  là  tín 
hiệu  tĩnh  thì  các  nhược  điểm  trên  không  có  ảnh  hưởng 
quan trọng, nhưng trên thực tế có nhiều tín hiệu chứa các 
thông số động như: trôi, nghiêng, biến đổi đột ngột, khởi 
đầu và  kết  thúc  các  sự  kiện, nên khi  sử dụng phương 
pháp Fourier sẽ không thể phát hiện sớm được những sự 
cố như NM. Để có  thể cải  thiện chất  lượng  tín hiệu đưa 
vào rơle có nhiều phương pháp xử lý tín hiệu khác nhau 
như  phép  biến  đổi  Stockwell,  KF,  phép  biến  đổi 
Wavelet...  Vì  vậy,  trong  bài  báo  này  nhóm  tác  giả  đề 
xuất phương pháp xử  lý  tín hiệu bằng KF để xây dựng 
mô hình rơle BVKC. 
2. Ứng dụng KF trong BVKC đặc tuyến khởi động 
vòng tròn đi qua gốc O (MHO) 
2.1. Đặc tuyến khởi động vòng tròn đi qua gốc O trong 
BVKC 
Đặc  tuyến  khởi  động MHO 
[1, 2] là đặc tuyến vòng tròn đi 
qua  gốc  O  (tổng  dẫn  MHO). 
Tổng trở khởi động của bảo vệ 
(BV) phụ thuộc vào góc φR. BV 
có độ nhạy cực đại khi φR = φRn 
hay  φR = φl.  BV  không  khởi 
động đối với ZR nằm trong phần 
tư  thứ  ba  của  mặt  phẳng  phức 
nên được gọi là BV tổng trở có hướng. Đặc tuyến thực tế 
không đi qua gốc  tọa độ O do bản  thân bộ phận so sánh 
không đủ  nhạy. Vì  thế, NM  đầu đường dây  gần  chỗ đặt 
BV có  thể BV sẽ không  làm việc, đoạn này gọi  là  vùng 
chết của BV. 
2.2. Cơ sở KF 
KF  [3]  là  thuật  toán  sử  dụng  chuỗi  các  giá  trị  đo 
lường,  bị  ảnh  hưởng  bởi  nhiễu  hoặc  sai  số,  để  ước 
đoán biến số nhằm tăng độ chính xác so với việc sử dụng 
duy nhất một giá trị đo lường. KF thực hiện phương pháp 
truy hồi đối với chuỗi các giá trị đầu vào bị nhiễu, nhằm 
tối ưu hóa giá trị ước đoán trạng thái của hệ thống. 
KF là phương pháp xử lý tín hiệu hiệu chỉnh tham số 
ước  lượng  dựa  trên  mẫu  liền  kề  trước  nó,  còn  phương 
pháp  Fourier  phải  sử  dụng  dữ  liệu  trong  một  cửa  sổ  tín 
hiệu, chẳng hạn như một chu kỳ để ước lượng tham số tín 
ISSN 1859-1531 - TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ ĐẠI HỌC ĐÀ NẴNG, SỐ 11(96).2015, QUYỂN 2 73 
hiệu nên có độ trễ lớn hơn, vì vậy KF có khả năng bám tín 
hiệu tốt hơn so với phương pháp xử lý tín hiệu Fourier. 
Quá  trình  ước  lượng  trạng  thái  của  KF  được  mô  tả 
theo phương trình sai phân tuyến tính sau: 
  1     ;
n
k k k k kX G X W X R (1) 
Trong đó: 
G  là  ma  trận  biến  đổi  trạng  thái  G  từ  thời  điểm  k-1 
sang thời điểm k. 
Wk là nhiễu quá trình; trong bài toán của bài báo này ta 
giả  thiết  là  nhiễu  trắng Gaussian với  kỳ vọng bằng 0 và 
ma trận tương quan được xác định bởi: 
( );
( ) ( )
0;
T
Q k n k
E W n W k
n k
  (2) 
Quá trình ước lượng phép đo của KF được mô tả theo 
phương trình sai phân tuyến tính sau: 
   ; 
n
k k k k kZ H X V Z R (3) 
Trong đó: 
H là ma trận của phép đo; 
Vk là nhiễu phép đo; trong bài toán của bài báo này ta 
giả  thiết  là  nhiễu  trắng Gaussian với  kỳ vọng bằng 0 và 
ma trận tương quan được xác định bởi: 
( );
( ) ( )
0;
T
R k n k
E V n V k
n k
  (4) 
Việc tính toán trong KF được chia làm hai giai đoạn: 
giai đoạn dự đoán và giai đoạn cập nhật. Trong giai đoạn 
dự đoán, số  liệu được  lấy ở  lần đo gần nhất và việc  tính 
toán dữ liệu được thực hiện trong giai đoạn cập nhật. 
Phương trình trong giai đoạn dự đoán: 
/ 1 1/ 1
/ 1  1/ 1    
k k k k k
k k k k
T
k kk
X G X
QGP G P
  (5) 
Phương trình trong giai đoạn cập nhật: 
 
1
/ 1  / 1
/   / 1
/ 1 
  / 1 / 1
/ 1
T T
k k k k k k k k k
k k k k k k
k k k k k k
k k k k k k
Y Z H
K
X
X X K Y
P I K H P
P H H P H R
  (6) 
Hình 2. Sơ đồ thuật toán của KF [4] 
2.3. Mô hình KF trong rơle BVKC sử dụng đặc tuyến 
khởi động MHO 
Mô  hình  của  KF  và  rơle  BVKC  sử  dụng  KF  được 
trình bày như ở Hình 3 và Hình 4. 
Tín hiệu từ biến điện áp (TU) và biến dòng điện (TI) 
sau khi được thêm 1 lượng nhiễu trắng Gaussian sẽ được 
lấy  mẫu để đưa vào  KF,  khi  đó  tín  hiệu được phân  tích 
thông qua KF. 
Hình 3. Mô hình KF xây dựng trên Matlab/Simulink [5] 
Hình 4. Mô hình rơle BVKC sử dụng KF trên Matlab/Simulink [6]
Xk-1, Pk-1 
Quá trình hiệu chỉnh 
- Tính hệ số khuếch đại của KF: 
- Giá trị hiệu chỉnh: 
- Hiệu chỉnh sai số hiệp phương sai: 
Quá trình dự đoán 
- Ước đoán trạng thái kế tiếp: 
-  Ước  đoán  sai  số  hiệp  phương 
sai kế tiếp: 
74 Huỳnh Đức Hoàn, Trần Xuân Khoa 
Với: 
  Phương sai đo lường: R =0.01; 
  Phương sai mô hình: 
5
5
10 0
0 10
Q
; 
  Ma trận chuyển đổi trạng thái: 
1 0
0 1
kG
; 
  Ma trận đo lường:   cos( ) sin( )kH k T k T  . 
Khi đó, tín hiệu qua KF sẽ cho giá trị biên độ và góc 
pha của dòng điện, điện áp từng pha. Giá trị tổng trở từng 
pha sẽ được tính toán dựa vào giá trị dòng điện và điện áp 
mà KF phân  tích được. Từ đó đi  so  sánh với  từng vùng 
tổng  trở  khởi  động.  Nếu  giá  trị  tổng  trở  NM  nằm  trong 
vùng  khởi  động  nào  thì  đưa  tín  hiệu  cắt  máy  cắt  tương 
ứng với vùng đó. Khi tổng trở nằm ngoài vùng khởi động 
thì bảo vệ sẽ không tác động. 
3. Kết quả mô phỏng 
Để  đánh  giá  hiệu  quả  làm  việc  của  mô  hình  rơle 
BVKC được xây dựng ở mục 2.3, mục này nhóm tác giả 
đề xuất lưới điện gồm hai nguồn cấp điện cho một phụ tải 
thông qua một đường dây có đặt BVKC ở hai đầu đường 
dây như Hình 5 và số liệu như Bảng 1. Ngoài ra để đánh 
giá  khả  năng  lọc  nhiễu  của  KF  tác  giả  cộng  thêm  một 
lượng nhiễu trắng Gaussian vào các tín hiệu đo lường của 
các TU và TI. Các điểm NM tính toán như sau: 
N1 – NM cách bảo vệ 1 (BV1) 190 km, được sử dụng 
để kiểm tra NM nằm trong vùng thứ hai của BV1 và vùng 
thứ nhất của bảo vệ 2 (BV2). 
N2 – NM cách BV1 và BV2 100 km, được sử dụng để 
kiểm tra NM nằm trong vùng thứ nhất của cả hai BV. 
Bảng 1. Thông số các phần tử 
Phần tử Thông số 
Nguồn 
Nút 1: Nút cân bằng công suất; 
f = 50 (Hz); U1 = 220 (kV). 
Nút 2: P = 300 (MW); U2 = 220 (kV); 
f = 50 (Hz). 
Đường dây 
R0 = R1 = 0.1 (Ω/km); 
L0 = L1 = 0.4/(2π50) (H/km); 
C0 = C1 = 10-12 (F/km); L = 200 (km). 
Phụ tải  S = 400 (MVA); cosφ = 1. 
Thông số của 
KF 
Vm = 1pu; theta = 0 (Rad). 
Phương sai đo lường: R = 0.01. 
Phương sai mô hình: 
5
5
10 0
0 10
Q
Thông số NM: 
N1, N2. 
Rg = 2 (Ω); tf = 0.2 (s). 
Nhiễu trắng 
Gaussian 
SNR = 20 (dB). 
Thông số rơle 
BVKC đặc 
tuyến khởi 
động MHO 
 Z1s = 66 (Ω), Z2s = 125 (Ω), Z3s =165 (Ω);
TMS: t1 = 0.05 (s), t2 = 0.3 (s), t3 = 0.6 (s). 
Hình 5. Mô hình mô phỏng rơle BVKC đặc tuyến khởi động MHO cho đường dây có hai nguồn cung cấp điện 
ISSN 1859-1531 - TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ ĐẠI HỌC ĐÀ NẴNG, SỐ 11(96).2015, QUYỂN 2 75 
Ngắn mạch 3 pha tại N1 (khi BV1 tác động): 
Hình 6. Kết quả dòng điện rơle BVKC đặc tuyến khởi động MHO của BV1 khi NM 3 pha tại N1; 
a) Dòng điện TI trước KF; b) Dòng điện TI sau KF; c) Phóng đại hình a; d) Phóng đại hình b 
Hình 7. Kết quả điện áp rơle BVKC đặc tuyến khởi động MHO của BV1 khi NM 3 pha tại N1; 
a) Điện áp TU trước KF; b) Điện áp TU sau KF; c) Phóng đại hình a; d) Phóng đại hình b 
0 0.2 0.4 0.6 0.8 1
-10
0
10
20
a) Dong dien truoc KF
t (s)
In
o
rm
a
l 
(A
)
0.5 0.505 0.51 0.515 0.52
-10
0
10
c) Phong dai hinh a
t (s)
In
o
rm
a
l 
(A
)
0 0.2 0.4 0.6 0.8 1
-10
0
10
20
b) Dong dien sau KF
t (s)
Ik
a
lm
a
n
 (
A
)
0.5 0.505 0.51 0.515 0.52
-10
0
10
d) Phong dai hinh b
t (s)
Ik
a
lm
a
n
 (
A
)
0 0.2 0.4 0.6 0.8 1
-200
0
200
a) Dien ap truoc KF
t (s)
U
n
o
rm
a
l 
(V
)
0.5 0.505 0.51 0.515 0.52
-100
0
100
c) Phong dai hinh a
t (s)
U
n
o
rm
a
l 
(V
)
0 0.2 0.4 0.6 0.8 1
-200
0
200
a) Dien ap sau KF
t (s)
U
k
a
lm
a
n
 (
V
)
0.5 0.505 0.51 0.515 0.52
-100
0
100
d) Phong dai hinh b
t (s)
U
k
a
lm
a
n
 (
V
)
-80 -60 -40 -20 0 20 40 60 80 100 120
0
20
40
60
80
100
120
140
160
Dac tinh MHO
jX
 (
O
h
m
)
R (Ohm)
Tong tro DD
Vung I
Vung II
Vung III
Zfault
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
T
ri
p
Hình 8. Kết quả Zfault của BV1 khi NM 
3 pha tại N1 
Hình 9. Tín hiệu cắt máy cắt của BV1 
 khi NM 3 pha tại N1 
76 Huỳnh Đức Hoàn, Trần Xuân Khoa 
Ngắn mạch 3 pha tại N1 (khi BV2 tác động): 
Hình 10. Kết quả dòng điện rơle BVKC đặc tuyến khởi động MHO của BV2 khi NM 3 pha tại N1; 
a) Dòng điện TI trước KF; b) Dòng điện TI sau KF; c) Phóng đại hình a; d) Phóng đại hình b 
Hình 11. Kết quả điện áp rơle BVKC đặc tuyến khởi động MHO của BV2 khi NM 3 pha tại N1; 
a) Điện áp TU trước KF; b) Điện áp TU sau KF; c) Phóng đại hình a; d) Phóng đại hình b 
0 0.2 0.4 0.6 0.8 1
-100
0
100
a) Dong dien truoc KF
t (s)
In
o
rm
a
l 
(A
)
0.25 0.255 0.26 0.265 0.27
-10
0
10
c) Phong dai hinh a
t (s)
In
o
rm
a
l 
(A
)
0 0.2 0.4 0.6 0.8 1
-100
0
100
b) Dong dien sau KF
t (s)
Ik
a
lm
a
n
 (
A
)
0.25 0.255 0.26 0.265 0.27
-10
0
10
d) Phong dai hinh b
t (s)
Ik
a
lm
a
n
 (
A
)
0 0.2 0.4 0.6 0.8 1
-200
0
200
a) Dien ap truoc KF
t (s)
U
n
o
rm
a
l 
(V
)
0.25 0.255 0.26 0.265 0.27
-100
0
100
c) Phong dai hinh a
t (s)
U
n
o
rm
a
l 
(V
)
0 0.2 0.4 0.6 0.8 1
-200
0
200
a) Dien ap sau KF
t (s)
U
k
a
lm
a
n
 (
V
)
0.25 0.255 0.26 0.265 0.27
-100
0
100
d) Phong dai hinh b
t (s)
U
k
a
lm
a
n
 (
V
)
-80 -60 -40 -20 0 20 40 60 80 100 120
0
20
40
60
80
100
120
140
160
Dac tinh MHO
jX
 (
O
h
m
)
R (Ohm)
Tong tro DD
Vung I
Vung II
Vung III
Zfault
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
T
ri
p
Hình 12. Kết quả Zfault của BV2 khi NM 
3 pha tại N1 
Hình 13. Tín hiệu cắt máy cắt của BV2 
 khi NM 3 pha tại N1 
ISSN 1859-1531 - TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ ĐẠI HỌC ĐÀ NẴNG, SỐ 11(96).2015, QUYỂN 2 77 
Tương tự khi NM ở N2, ta có kết quả của BV1 và BV2 như Bảng 2 và 3: 
Bảng 2. Kết quả tổng trở và thời gian tác động của BV1 
Vị trí điểm 
NM cách BV1 
(km) 
Tổng trở khi NM (Ω)  Thời gian tác 
động của rơle (s) 
Vùng bảo 
vệ 
Pha A  Pha B  Pha C 
190 (N1)  21.66 + j75.8  21.14 + j76.53  21.3 + j76.11  0.304  Vùng II 
100 (N2)  14.03 + j39.29  13.82 + j39.81  14.16 + j39.46  0.0531  Vùng I 
Bảng 3. Kết quả tổng trở và thời gian tác động của BV2 
Vị trí điểm 
NM cách BV2 
(km) 
Tổng trở khi NM (Ω)  Thời gian tác 
động của rơle (s) 
Vùng bảo 
vệ 
Pha A  Pha B  Pha C 
10 (N1)  3.192 + j4.029  3.195 + j4.05  3.209 + j4.044  0.0505  Vùng I 
100 (N2)  13.9 + j40.12  13.9 + j40.47  14.19 + j40.2  0.0531  Vùng I 
Nhận xét: 
Từ các hình 6, 7, 10 và 11 ta thấy tín hiệu dòng điện 
và điện áp sau KF cho tín hiệu đầu ra ít nhiễu và bám tín 
hiệu tốt nên tín hiệu đưa vào BV sẽ chính xác, vì vậy BV 
sẽ tác động nhanh hơn và hạn chế được tác động nhầm do 
nhiễu gây ra. 
Kết quả từ Bảng 2 và 3 cho ta thấy rằng ứng với mỗi 
điểm NM nằm  trong những vùng BV khác nhau  thì  thời 
gian  tác động  là khác nhau, khi NM trong vùng BV nào 
thì tác động tương ứng với thời gian đặt của vùng đó. NM 
trong cùng một vùng BV, nhưng vị trí NM nào gần điểm 
đặt BV hơn thì thời gian tác động sẽ nhanh hơn. 
4. Kết luận 
Bài  báo  này  đã  ứng  dụng  KF  trong  rơle  BVKC  sử 
dụng  đặc  tuyến  khởi  động  MHO  mô  phỏng  trong  thời 
gian thực trên Matlab/Simulink. Sơ đồ lưới điện gồm hai 
nguồn  cấp  điện  cho  một  phụ  tải  thông  qua  đường  dây 
được  khảo  sát  để  áp  dụng  mô  hình  rơle  đã  đề  xuất;  tín 
hiệu  đưa  vào  mô  hình  rơle  được  thêm  một  lượng  nhiễu 
trắng Gaussian để thấy được khả năng lọc nhiễu của KF ở 
tín hiệu ra. 
Các  kết  quả  mô  phỏng  đã  kiểm  chứng  được  chức 
năng, đặc tuyến MHO của rơle làm việc chính xác và cho 
thấy được  tín hiệu qua KF  ít  nhiễu hơn so với  trước khi 
đưa  vào  bảo  vệ.  Mô  hình  của  rơle  được  tích  hợp  trong 
Matlab/Simulink  nên  dễ  dàng  áp  dụng  để  nghiên  cứu 
BVKC bằng các phương pháp xử lý tín hiệu hiện đại khác 
nhau trong hệ thống điện. 
Từ  mô  hình  trên  ta  có  thể  xây  dựng  các  mô  hình 
BVKC bằng KF để thay thế BV cho các kiểu đường dây 
truyền  tải  có  hai  nguồn  cung  cấp,  ba  nguồn  cung  cấp 
thường  dùng  phương  pháp  biến  đổi  Fourier  Từ  đó 
ứng dụng vào  cho đường dây  siêu  cao áp 500 kV Việt 
Nam trong tương lai. 
TÀI LIỆU THAM KHẢO 
[1] Lê Kim Hùng, Đoàn Ngọc Minh Tú, Bảo vệ rơle và tự động hóa, 
NXB Giáo dục, 1998. 
[2] Nguyễn Hoàng Việt, Bảo vệ rơle và tự động hóa trong hệ thống 
điện, NXB Đại học Quốc gia TP. Hồ Chí Minh, 2005. 
[3] Greg  Welch,  Gary  Bishop,  An Introduction to the Kalman filter, 
Department of Computer Science University of North Carolina at 
Chapel Hill, 2006. 
[4] Hisham Odeh Alrawashdeh, An adaptive Kalman filter for voltage 
sag detection in power systems, Western Michigan University, US, 
2014. 
[5] John  Wiley,  Kalman filtering theory and practice using 
Matlab,Published simultaneously in Canada, 2008. 
[6]  Li-Cheng  Wu,  Chih-Wen  Liu, Modeling and testing of a digital 
distance relay using Matlab/Smulink,  IEEE  Department  of 
Electrical  Engineering,  National  Taiwan  University,  Taipei, 
Taiwan, 2005. 
(BBT nhận bài: 26/07/2015, phản biện xong: 15/09/2015)