Tính toán điện từ trường bằng phương pháp tích phân số - Ứng dụng cho bài toán có cấu trúc dạng dây

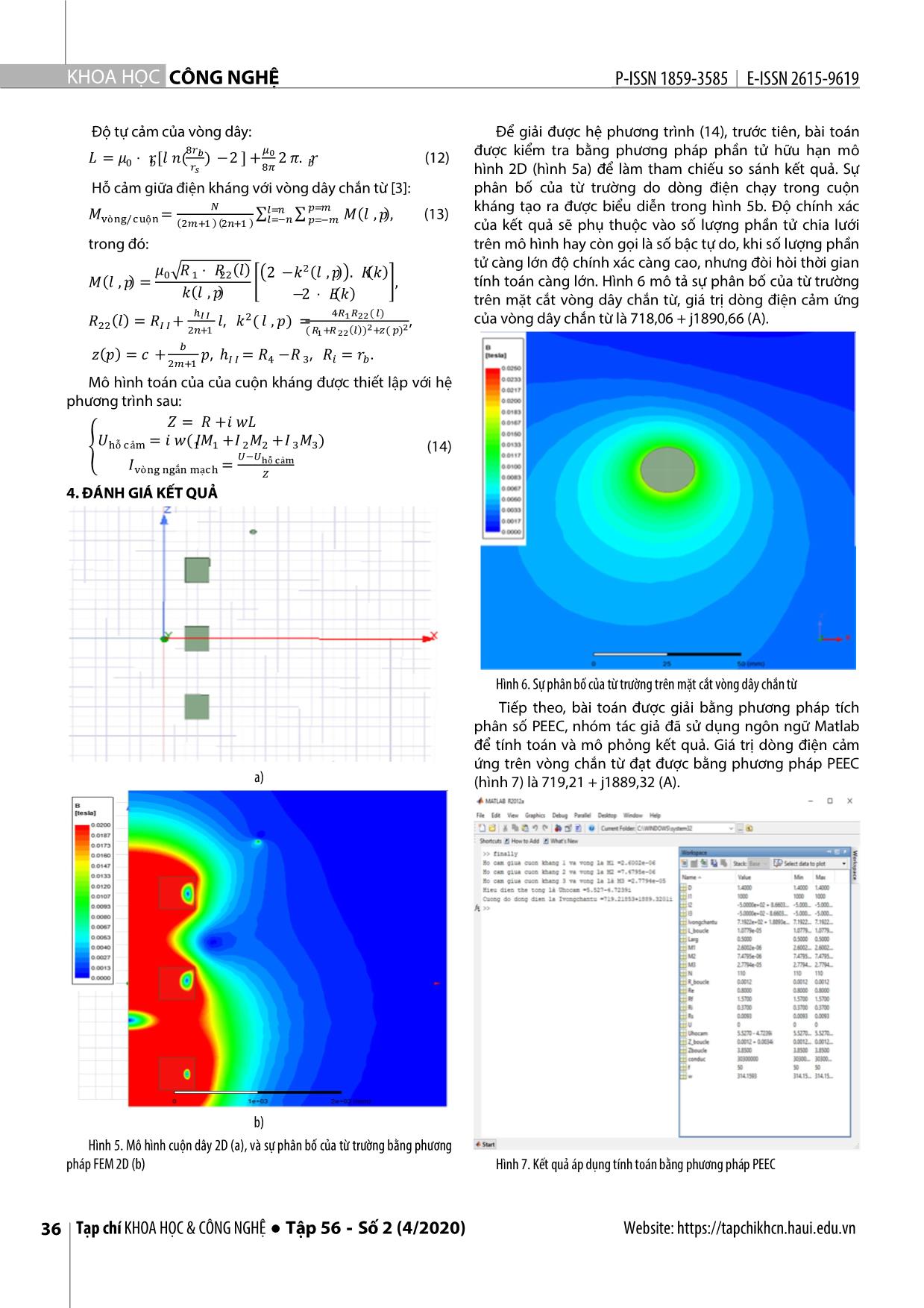
c fields in the space and variation in time. - 3]. Với các thiết bị điện có cấu trúc hình học đơn giản, 
In order to analyze this problem, in this paper, a partial element equivalent circuit is người ta có thể xác định được một đáp án giải tích chính 
applied to compute distributions of electromagnetic fields and induction currents in xác. Tuy nhiên, thực tế chứng minh rằng với cấu trúc thiết 
turn windings, where occuring some difficuilties as applying directly by a finite bị điện phức tạp, phương pháp giải tích không thể thực 
element method or a finite differential method, because of the big degree of 
 hiện được mà phải giải tìm nghiệm gần đúng bằng phương 
freedoms, leading to a big size of matric and spending a lot of time for 
 pháp số. 
computation. The obtained results will be compared with the simulation results of 
commercial software. Các phương pháp số được ứng dụng khá phổ biến 
 trong mô phỏng tính toán trường điện từ: Phương pháp 
 Keywords: Electromagnetics, Induction current, finite element method, 
 phần tử hữu hạn (FEM), phương pháp sai phân hữu hạn 
partial element equivalent circuit. 
 (FDM), phương pháp phần tử biên (BEM) và phương pháp 
Viện Điện, Trường Đại học Bách khoa Hà Nội tích phân số (IEM) 
*Email: tung.leduc1@hust.edu.vn Trong đó, phương pháp FEM là một phương pháp rất 
Ngày nhận bài: 18/02/2020 thông dụng [1, 4]. Ưu điểm của phương pháp này là tính 
Ngày nhận bài sửa sau phản biện: 26/3/2020 tổng quát, có khả năng mô phỏng thiết bị có cấu trúc khác 
Ngày chấp nhận đăng: 24/4/2020 nhau từ nhiều vật liệu (dẫn điện, cách điện, vật liệu từ,) ở 
 Website: https://tapchikhcn.haui.edu.vn Vol. 56 - No. 2 (Apr 2020) ● Journal of SCIENCE & TECHNOLOGY 33
 KHOA H ỌC CÔNG NGHỆ P - ISSN 1859 - 3585 E - ISSN 2615 - 961 9 
 dạng bài toán tuyến tính lẫn phi tuyến. Tuy nhiên, nhược   
 () = () = ∫  , (2) 
 điểm của phương pháp FEM là khó khăn trong việc tính    
 toán với các loại thiết bị có cấu trúc dạng vỏ mỏng và đặc trong đó: r là khoảng cách giữa điểm lấy tích phân và 
 biệt là cấu trúc dạng dây. điểm P (điểm xét sợi dẫn j), Ij là cường độ dòng điện trong 
 Mô hình hóa dây dẫn: từ trường thay đổi rất nhiều ở vật dẫn j, Sj là diện tích mặt cắt sợi dẫn j và Vj là thể tích của 
 vùng lân cận và bên trong dây dẫn, việc mô phỏng đúng sợi dẫn. 
 trường điện từ ở gần vật dẫn có xét đến hiệu ứng bề mặt Điện thế tạo bởi dòng điện Ij qua phần sợi dẫn k được 
 (skin effect) và hiệu ứng gần (proximity effect) tạo ra các tính: 
 phương trình phần tử hữu hạn với số bậc tự do lớn, dẫn tới    
 Φ = ∫  ∙  = ∫ ∫  (3) 
 cấu trúc ma trận tính toán rất lớn. Nếu áp dựng phương       
 pháp FEM để giải, yêu cầu máy tính có hình rất lớn và chi Hệ số hỗ cảm giữa 2 sợi dây dẫn được xác định bởi: 
 phí khá tốn kém và thậm chí không thể thực hiện được. 
    
  = = ∫ ∫  (4) 
 Để khắc phục được những khó khăn này, nhóm tác giả      
 đã áp dụng và phương pháp tích phân số, trong đó kể đến 
 Hệ số hỗ cảm  chỉ phụ thuộc vào kích thước và vị trí 
 phương pháp PEEC để nghiên cứu điện từ trường trong các của hai sợi dẫn k và j, có thể tính bằng giải tích. Điện áp trên 
 thiết bị có cấu trúc dạng dây [2, 3]. Ưu điểm của phương dây dẫn k được xác định: 
 pháp nằm ở chỗ không phải chia lưới vùng không khí bao 
 ∑
 quanh (như phương pháp FEM) đối tượng tính toán giảm  =  ∙  +   , (5) 
 thời gian cũng như khối lượng tính toán. Mạch điện thu trong đó,  là tần số góc,  là nội trở của sợi dẫn k. 
 được sẽ được tiếp tục tính toán từ đó hiện tượng điện từ 2.2. Sự hỗ cảm của hai sợi dây đồng trục 
 của các thiết bị điện sẽ được nghiên cứu trong một hệ 
 thống có tính đến các sự ảnh hưởng của những thiết bị Xét hai cuộn dây đồng trục L1 và L2 (hình 1) mang điện 
 điện khác. và đặt gần nhau trong không khí. Công thức (4) cho thấy hỗ 
 cảm không bị ảnh hưởng bởi vật liệu mà chỉ phụ thuộc vào 
 2. MÔ HÌNH HOÁ TRƯỜNG ĐIỆN TỪ dòng điện và tính chất hình học của hệ thống. Ở tần số 
 2.1. Phương pháp tích phân số thấp, độ hỗ cảm thay đổi rất ít trong mặt cắt ngang. Áp 
 Như đã phân tích ở phần 1, mặc dù phương pháp tích dụng công thức Neumann [6], độ hỗ cảm  của hai dây 
 phân số không tổng quát như phương pháp FEM. Tuy dẫn L1 và L2 và được xác định: 
 nhiên, đây là phương pháp thích hợp khi mô phỏng những  
  = ∬ , (6) 
 thiết bị điện có dạng phức tạp có nhiều không khí bao   
 quanh. Một trong những phương pháp tích phân số được trong đó, r là khoảng cách giữa dL1 và dL2 và  là độ từ thẩm 
 ưa thích đối với các nhà nghiên cứu là: phương pháp PEEC. của cuộn dây. 
 Phương pháp PEEC được phát triển bởi Ruehli [5], đây là 
 một trong những phương pháp số thích hợp cho bài toán 
 trường điện từ có xét đến sự ảnh hưởng của tương thích 
 điện từ (EMC) và nhiễu điện từ EMI Phương pháp cũng 
 cho phép mô phỏng hiện tượng điện từ bao gồm các thành 
 phần điện trở, điện cảm, hỗ cảm, điện dung (RLMC) mà các 
 giá trị các phần tử RLMC được tính bằng tích phân [3]. 
 Xét mô hình toán học của bức xạ điện trường E xét trên 
 một thể tích dây dẫn Nb được đặt gần nguồn điện từ trong 
 không khí, áp dụng phương pháp PEEC, ta có: 
 (,) (,)
 (, ) = + + ∇Φ(, ), (1) 
  
 trong đó:  là cường độ điện trường, J là mật độ dòng 
 điện trong vật dẫn, A véc tơ từ thế, Φ là véc tơ điện thế vô 
 hướng và  độ dẫn điện của vật dẫn. 
 Một dây dẫn có diện tích mặt cắt ngang không đổi dọc 
 theo chiều dài của nó có thể được coi là một bó các sợi 
 Hình 1. Hai cuộn dây đồng trục L1 và L2 với mặt cắt hình chữ nhật 
 song song, mỗi sợi dẫn có diện tích mặt cắt ngang  và 
  Theo hệ tọa độ trụ, nếu 2 cuộn dây được quấn chặt chẽ 
 mang dòng điện  . Mật độ dòng J giả định là không đổi 
  và cách điện giữa các vòng dây là tương đối mỏng. Dòng 
 dọc theo chiều dài của sợi dẫn nhưng thay đổi từ sợi dẫn điện trong cuộn dây có thể được xem là phân bố đều ở 
 này sang sợi dẫn khác. 
 toàn bộ mặt cắt với mật độ dòng điện lần lượt là JI và JII. Khi 
 Phương trình của véc tơ từ thế  do dòng  của sợi dẫn đó, độ hỗ cảm giữa 2 cuộn dây đồng trục có mặt cắt hình 
 j gây ra được xác định: chữ nhật có số vòng là N1 và N2 được xác định: 
34 Tạp chí KHOA HỌC & CÔNG NGHỆ ● Tập 56 - Số 2 (4/2020) Website: https://tapchikhcn.haui.edu.vn 
P-ISSN 1859-3585 E-ISSN 2615-9619 SCIENCE - TECHNOLOGY 
         
  ∫ ∫ ∫ ∫ ∫  = ,  = , 
  =      (7a)    
 ()()()()
 ℎ =  − , ℎ =  − , 
   
  = ( −  ) +  +  − 2  cos  (7b)  
       (, ) =  +  + , 
 Để đảm bảo tính chính xác và độ tin cậy của công thức () ()
tính độ hỗ cảm (7a-b) thu được từ phương pháp tích phân,  = −,  ,0,  , , à  = −,  ,0,  , . 
sử dụng phương pháp Filament để chia cuộn dây thành 3. BÀI TOÁN ÁP DỤNG 
nhiều sợi tròn đồng trục để tính độ hỗ cảm của hai cuộn 
 Xét một hệ thống gồm kháng điện 3 pha được sử dụng 
dây tròn có tiết diện hình chữ nhật, đó là: 
 để hạn chế dòng điện điện ngắn mạch tại phía thứ cấp của 
 
 2  trạm biến áp phân phối (hình 3). 
  = 1 −  () − (), 
  2
  
 với  =  . (8) 
 () 
 Trong đó: E và K là tích phân đường elip loại một và loại 
hai lần lượt được xác định: 
 /   /
  = ∫ (1 −   ) , 
 / 
  = ∫ . (9a-b) 
  ()/
 Hình 3. Mô hình cuộn kháng 3 pha và vòng ngắn mạch 
 Các thông số của cuộn kháng được cho như sau: 
 cuộn 1 có dòng điện ia = 1000 sin  (A), cuộn 2 có ib = 
 
 1000 sin ( + 120 ) (A), cuộn 3 có ic = 1000 sin ( −
 
 120 ) (A), đường kính ngoài e = 1,6m, đường kính trong 
 Hình 2. Mô hình chia lưới cuộn dây i = 0,74 m, độ dày e0 = 0,5m, khoảng cách giữa các cuộn 
 e = 1,4m. Thông số của vòng ngắn mạch (vòng chắn từ) 
 Do kích thước của cuộn dây là hữu hạn, nên chia 2 cuộn nt
 có thông số: r = 9,25mm (bán kính mặt cắt), điện trở suất 
thành các lưới gồm nhiều sợi dây như hình 2. Mặt cắt s 
  = 3,03. 10Ω. 
ngang của 2 cuộn được chia lần lượt thành (2N + 1) ×
(2K + 1) ô và (2n + 1) × (2m + 1) ô. Mỗi ô trên mặt cắt Từ mô hình cuộn kháng, sơ đồ mạch điện thay thế 
chứa 1 sợi và dòng điện trên mỗi sợi dây là như nhau. tương đương được xác định theo hình 4. 
 Theo công thức (7a-b), sự hỗ cảm của từng cặp sợi dây rs
 L R M
như công thức được xác định: propre boucle/bobine
     Section
  ∑ ∑ ∑ ∑ (,,,)
  =    , (10) 
 ()()()()
 rb
 trong đó: U
 
  (,,,) Mboucle/plaque
 ()() 1 −  (, ℎ, , )
  =   , 
 (,,,) −((, ℎ, , ))
 Boucle
  () ()
 (, ℎ, , ) =   , 
   
 ()() (,)
  Hình 4. Mạch điện thay thế tương đương 
  (ℎ) =  +  ℎ, với ℎ = −,  ,0,  , , 
   () Nội trở vòng dây ngắn mạch được xác định: 
 
  () =  +  , với  = −,  ,0,  , , .
   ()  =   (11) 
 .
 Website: https://tapchikhcn.haui.edu.vn Vol. 56 - No. 2 (Apr 2020) ● Journal of SCIENCE & TECHNOLOGY 35
 KHOA H ỌC CÔNG NGHỆ P - ISSN 1859 - 3585 E - ISSN 2615 - 961 9 
 Độ tự cảm của vòng dây: Để giải được hệ phương trình (14), trước tiên, bài toán 
   được kiểm tra bằng phương pháp phần tử hữu hạn mô 
  =  ⋅ [( ) − 2] + 2.  (12) 
   hình 2D (hình 5a) để làm tham chiếu so sánh kết quả. Sự 
 Hỗ cảm giữa điện kháng với vòng dây chắn từ [3]: phân bố của từ trường do dòng điện chạy trong cuộn 
   kháng tạo ra được biểu diễn trong hình 5b. Độ chính xác 
  = ∑ ∑ (, ), (13) 
 ò/ộ ()()   của kết quả sẽ phụ thuộc vào số lượng phần tử chia lưới 
 trong đó: trên mô hình hay còn gọi là số bậc tự do, khi số lượng phần 
 tử càng lớn độ chính xác càng cao, nhưng đòi hòi thời gian 
   ⋅  () 2 − (, ). ()
 (, ) =     , tính toán càng lớn. Hình 6 mô tả sự phân bố của từ trường 
 ( )
  ,  −2 ⋅ () trên mặt cắt vòng dây chắn từ, giá trị dòng điện cảm ứng 
   () của vòng dây chắn từ là 718,06 + j1890,66 (A). 
 () =  + ,  (, ) =  , 
  (()) ()
 
 () =  + , ℎ =  −  ,  =  . 
      
 Mô hình toán của của cuộn kháng được thiết lập với hệ 
 phương trình sau: 
  =  + 
 ỗ ả = ( +  + ) (14) 
 
  = ỗ ả
 ò ắ ạ 
 4. ĐÁNH GIÁ KẾT QUẢ 
 Hình 6. Sự phân bố của từ trường trên mặt cắt vòng dây chắn từ 
 Tiếp theo, bài toán được giải bằng phương pháp tích 
 phân số PEEC, nhóm tác giả đã sử dụng ngôn ngữ Matlab 
 để tính toán và mô phỏng kết quả. Giá trị dòng điện cảm 
 ứng trên vòng chắn từ đạt được bằng phương pháp PEEC 
 a) (hình 7) là 719,21 + j1889,32 (A). 
 b) 
 Hình 5. Mô hình cuộn dây 2D (a), và sự phân bố của từ trường bằng phương 
 pháp FEM 2D (b) Hình 7. Kết quả áp dụng tính toán bằng phương pháp PEEC 
36 Tạp chí KHOA HỌC & CÔNG NGHỆ ● Tập 56 - Số 2 (4/2020) Website: https://tapchikhcn.haui.edu.vn 
P-ISSN 1859-3585 E-ISSN 2615-9619 SCIENCE - TECHNOLOGY 
 Bảng 1. Kết quả so sánh của dòng điện cảm ứng trên vòng chắn bằng các LỜI CẢM ƠN 
phương pháp khác nhau Nghiên cứu này được tài trợ bởi Bộ Giáo dục và Đào tạo 
 Dòng điện Phương Phương Sai số Thời gian Thời gian trong đề tài mã số B2018-BKA-11-CtrVL. 
 cảm ứng pháp FEM pháp PEEC tính toán tính toán 
 trên vòng 2D (FEM 2D) (PEEC) 
 chắn 
 TÀI LIỆU THAM KHẢO 
 I 718,06 + 719,21 + 0,04% 2s 0,2s 
 vòng dây [1]. B. Stoev, G. Todorov, P. Rizov, G. Pagiatakis, and L. Dritsas, 2017. Finite 
 j1890,66 j1889,32 
 element analysis of rotating electrical machines - An educational approach. IEEE 
 Dựa vào bảng 1, có thể nhận thấy rằng, các kết quả đạt Glob. Eng. Educ. Conf. EDUCON, no. April, pp. 262–269. 
được từ phương pháp PEEC được kiểm chứng với kết quả 
 [2]. T. Le-Duc, O. Chadebec, J-M. Guichon, G. Meunier and Y. Lembeye, 2013. 
đạt được từ phương pháp FEM với mô hình 2D. Giá trị sai số 
 Coupling between Partial Element Equivalent Circuit Method and Magnetic Moment 
giữa hai phương pháp là nhỏ hơn 1%. Điều này chứng tỏ, 
 Method. The International Journal for Computation and Mathematics in Electrical 
giá trị đạt được từ phương pháp PEEC là đáng tin cậy. 
 and Electronic Engineering (COMPEL), Vol. 32, No. 1, pp. 383-395. 
 Để khảo sát thêm, hình 8 thể hiện từ trường dọc trục cắt 
 [3]. T. Le-Duc, G. Meunier, O. Chadebec, J-M. Guichon and L. Krähenbühl, 
qua mặt phẳng có vòng ngắn mạch trong 2 trường hợp 
 2013. A Simple Integral Formulation for the Modeling of Thin Conductive Shells. 
(có/không có vòng ngắn mạch) bằng phương pháp FEM The European Physical Journal Applied Physics (EPJ-AP), Vol.62, Iss.2. 
với mô hình 2D. Có thể nhận thấy rằng, từ trường tập trung 
tại mặt phẳng có chứa vòng ngắn mạch và giảm nhanh khi [4]. V. S. - and G. S., 2011. Calculation of Electromagnetic Fields in Electrical 
khoảng cách tăng lên. Ở khoảng cách 1m xa khỏi mặt Machines using Finite Elements Method. Int. J. Eng. Ind., vol. 2, no. 1, pp. 21–29. 
phẳng có vòng mạch, từ trường giảm về cỡ 1mT. [5]. C. Hoer and C. Love, 1965. Exact inductance equations for rectangular 
 conductors with applications to more complicated geometries. J. Res. Natl. Bur. 
 Stand. Sect. C Eng. Instrum., vol. 69C, no. 2, p. 127. 
 [6]. M. V. K. C. Salon, Sheppard, 1999. Numerical Methods in 
 Electromagnetism. 
 [7]. A. E. Ruehli, 1974. Equivalent Circuit Models for Three-Dimensional 
 Multiconductor Systems. IEEE Trans. Microw. Theory Tech., vol. 22, no. 3, pp. 
 216–221. 
 [8]. G. Zhong and C. K. Koh, 2002. Exact closed form formula for partial 
 mutual inductances of on-chip interconnects. Proc. - IEEE Int. Conf. Comput. Des. 
 VLSI Comput. Process., pp. 428–433. 
 AUTHORS INFORMATION 
 Pham Hong Hai, Le Duc Tung, Dang Quoc Vuong, Pham Van Binh 
 School of Electrical Engineering, Hanoi Unviversity of Science and Technology 
 Hình 8. Sự phân bố của từ trường dọc trục cắt qua mặt phẳng có vòng 
chắn từ 
5. KẾT LUẬN 
 Phương pháp tích phân số PEEC với “source code 
Matlab” đã được nhóm tác giả áp dụng thành công trong 
việc tính toán, mô phỏng từ trường và dòng điện cảm ứng 
trên vòng chắn (bảng 1). Phương pháp đã chỉ ra được ưu 
điểm là giảm thời gian cũng như khối lượng tính toán. Kết 
quả đạt được từ phương pháp sẽ cho các nhà nghiên cứu 
nhận biết được phạm vi ảnh hưởng của trường điện từ đối 
với các thiết bị xung quanh và đặc biệt là đối với cơ thể con 
người khi tham gia quản lý vận hành. Các kết quả cũng 
được so sánh với kết quả đạt được từ phần mềm thương 
mại dựa trên phương pháp phần tử hữu hạn. Đây cũng là 
cơ sở để minh chứng cho hướng đi đúng đắn của nghiên 
cứu và tạo tiền đề cho các nghiên cứu tổng quát tiếp theo. 
 Website: https://tapchikhcn.haui.edu.vn Vol. 56 - No. 2 (Apr 2020) ● Journal of SCIENCE & TECHNOLOGY 37