Thiết kế phần cứng bộ tạo nhiễu gauss tương quan, ứng dụng trong hệ thống kiểm tra và đánh giá chất lượng các bộ phát hiện ra đa

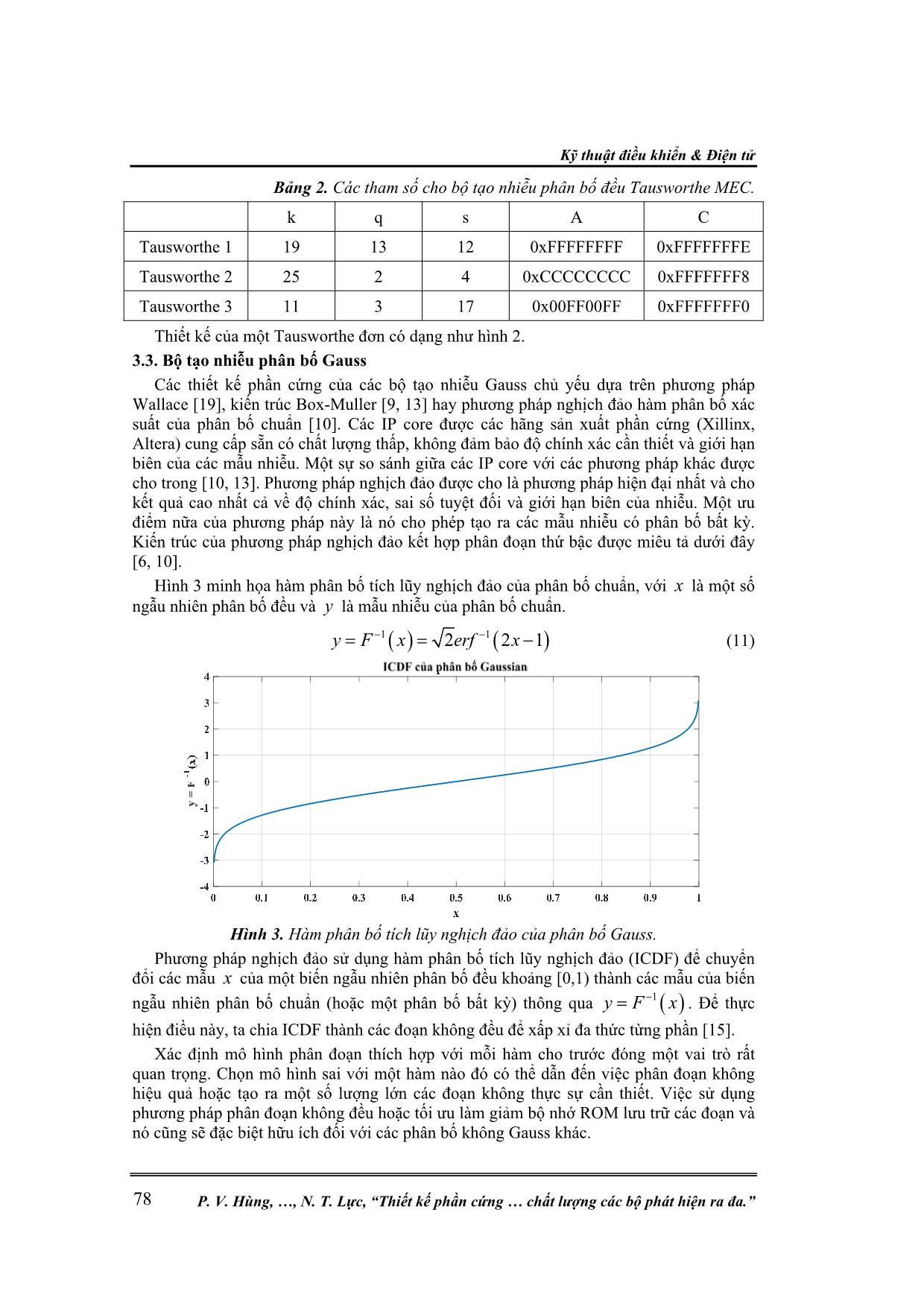
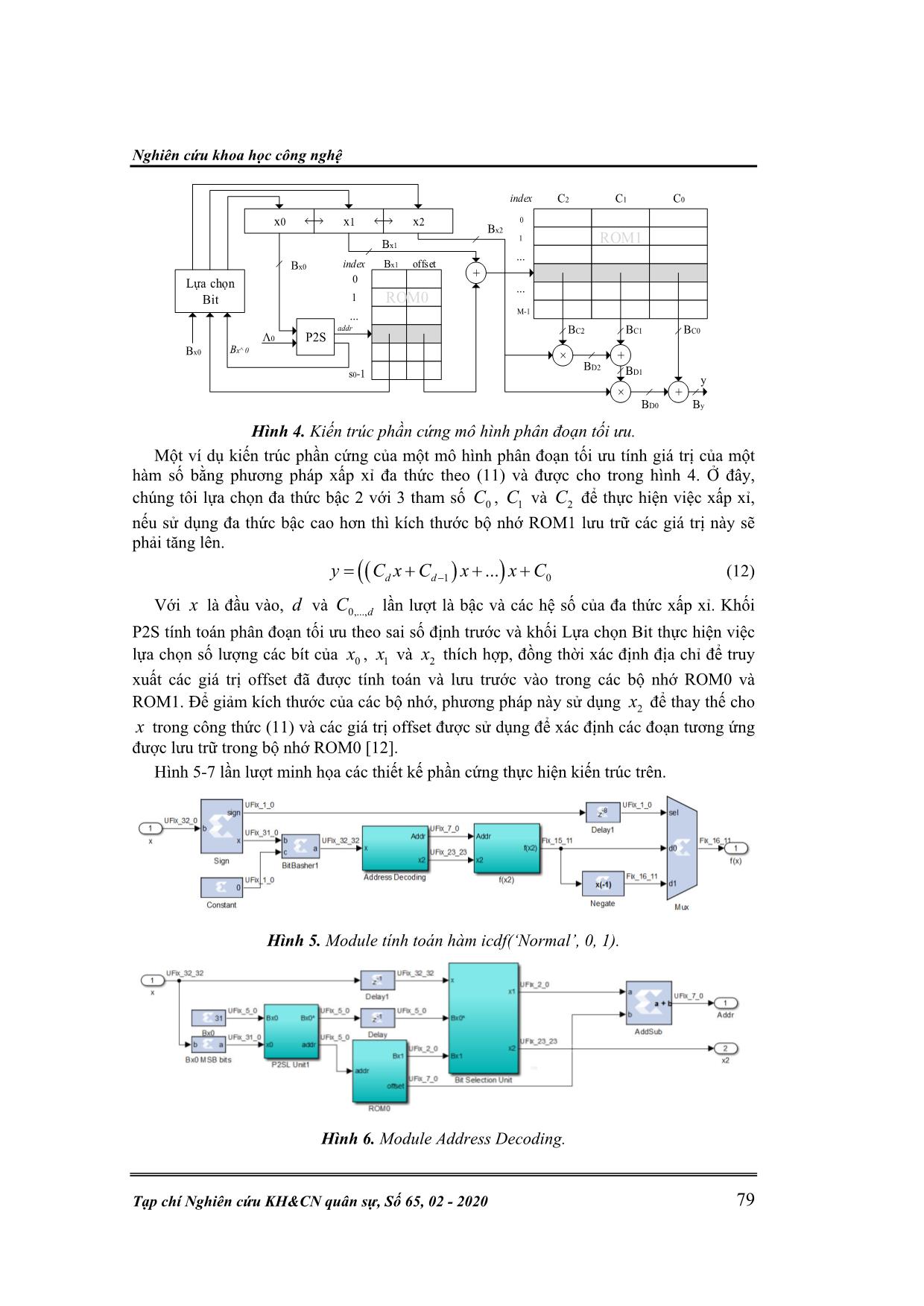
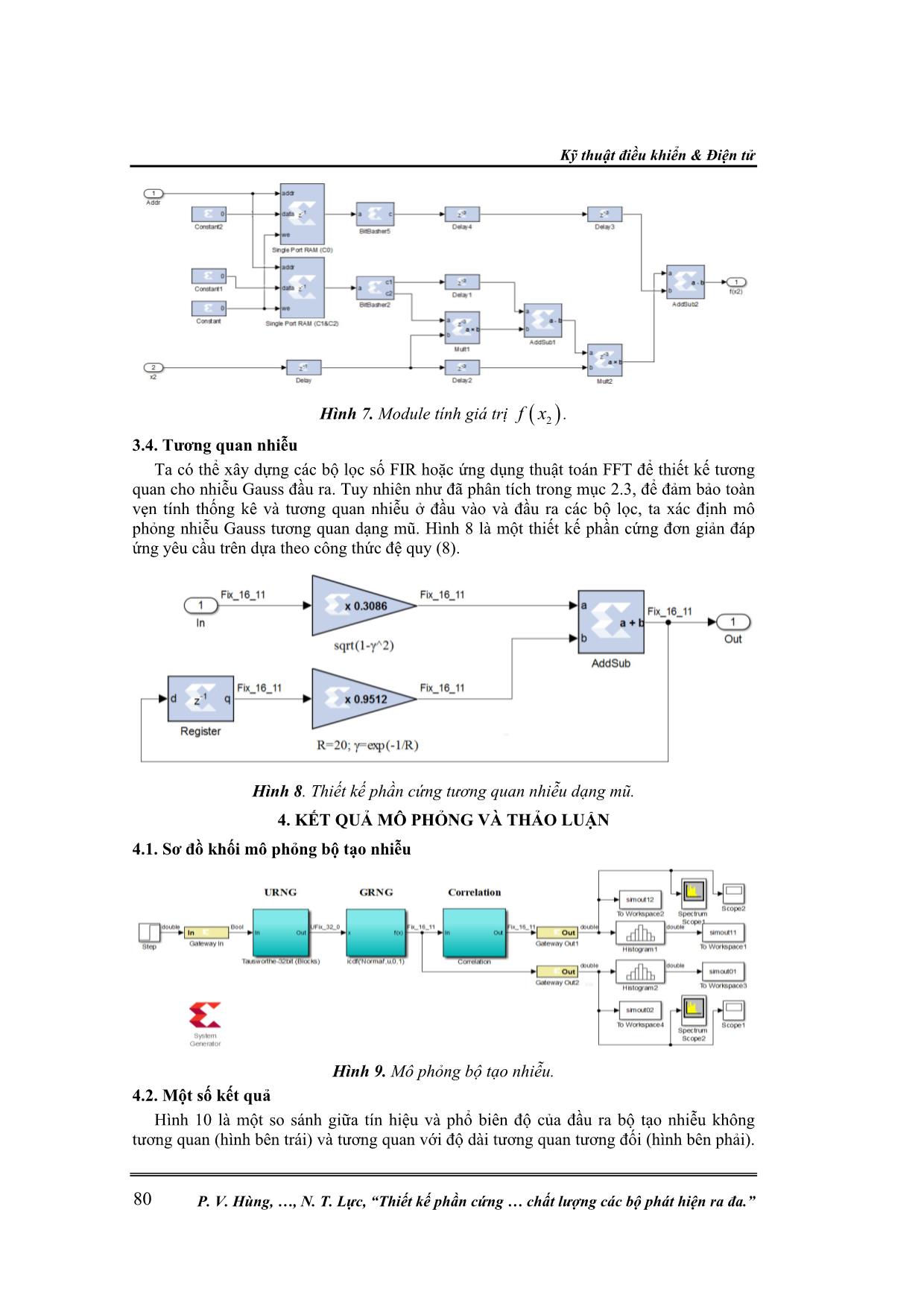
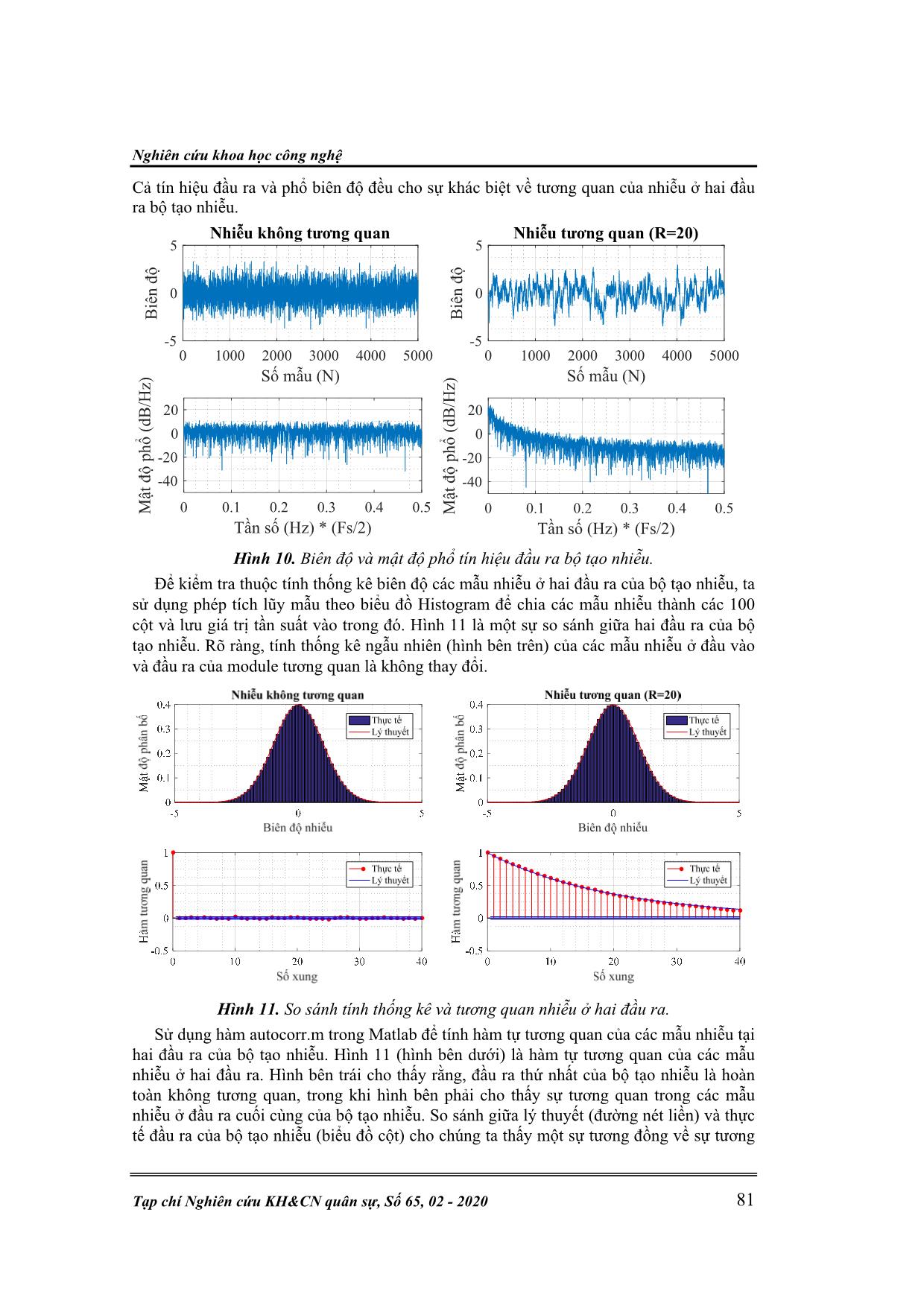
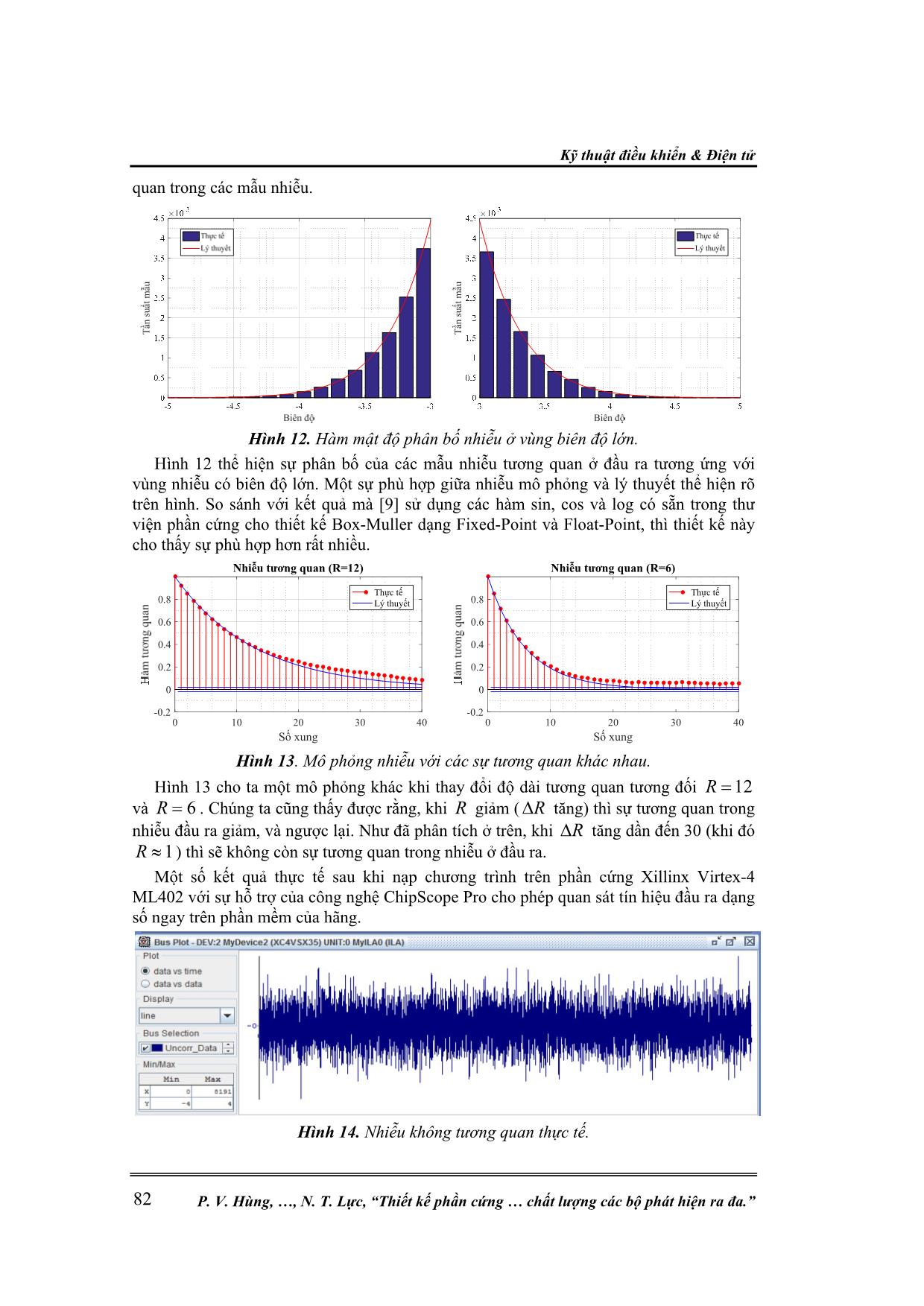
t số sự lựa chọn các tham số cho bộ Tausworthe MEC kết hợp từ 3 bộ Tausworthe 
đơn được chứng minh và đưa ra trong [11]. Ở đây, chúng tôi lựa chọn các giá trị tham số 
cho bộ tạo nhiễu đang xây dựng như trong bảng 2. 
Kỹ thuật điều khiển & Điện tử 
P. V. Hùng, , N. T. Lực, “Thiết kế phần cứng  chất lượng các bộ phát hiện ra đa.” 78 
Bảng 2. Các tham số cho bộ tạo nhiễu phân bố đều Tausworthe MEC. 
 k q s A C 
Tausworthe 1 19 13 12 0xFFFFFFFF 0xFFFFFFFE 
Tausworthe 2 25 2 4 0xCCCCCCCC 0xFFFFFFF8 
Tausworthe 3 11 3 17 0x00FF00FF 0xFFFFFFF0 
Thiết kế của một Tausworthe đơn có dạng như hình 2. 
3.3. Bộ tạo nhiễu phân bố Gauss 
Các thiết kế phần cứng của các bộ tạo nhiễu Gauss chủ yếu dựa trên phương pháp 
Wallace [19], kiến trúc Box-Muller [9, 13] hay phương pháp nghịch đảo hàm phân bố xác 
suất của phân bố chuẩn [10]. Các IP core được các hãng sản xuất phần cứng (Xillinx, 
Altera) cung cấp sẵn có chất lượng thấp, không đảm bảo độ chính xác cần thiết và giới hạn 
biên của các mẫu nhiễu. Một sự so sánh giữa các IP core với các phương pháp khác được 
cho trong [10, 13]. Phương pháp nghịch đảo được cho là phương pháp hiện đại nhất và cho 
kết quả cao nhất cả về độ chính xác, sai số tuyệt đối và giới hạn biên của nhiễu. Một ưu 
điểm nữa của phương pháp này là nó cho phép tạo ra các mẫu nhiễu có phân bố bất kỳ. 
Kiến trúc của phương pháp nghịch đảo kết hợp phân đoạn thứ bậc được miêu tả dưới đây 
[6, 10]. 
Hình 3 minh họa hàm phân bố tích lũy nghịch đảo của phân bố chuẩn, với x là một số 
ngẫu nhiên phân bố đều và y là mẫu nhiễu của phân bố chuẩn. 
 1 12 2 1y F x erf x (11) 
Hình 3. Hàm phân bố tích lũy nghịch đảo của phân bố Gauss. 
Phương pháp nghịch đảo sử dụng hàm phân bố tích lũy nghịch đảo (ICDF) để chuyển 
đổi các mẫu x của một biến ngẫu nhiên phân bố đều khoảng [0,1) thành các mẫu của biến 
ngẫu nhiên phân bố chuẩn (hoặc một phân bố bất kỳ) thông qua 1y F x . Để thực 
hiện điều này, ta chia ICDF thành các đoạn không đều để xấp xỉ đa thức từng phần [15]. 
Xác định mô hình phân đoạn thích hợp với mỗi hàm cho trước đóng một vai trò rất 
quan trọng. Chọn mô hình sai với một hàm nào đó có thể dẫn đến việc phân đoạn không 
hiệu quả hoặc tạo ra một số lượng lớn các đoạn không thực sự cần thiết. Việc sử dụng 
phương pháp phân đoạn không đều hoặc tối ưu làm giảm bộ nhớ ROM lưu trữ các đoạn và 
nó cũng sẽ đặc biệt hữu ích đối với các phân bố không Gauss khác. 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số 65, 02 - 2020 79
x0
Lựa chọn 
Bit
P2S
x1 x2
× +
× +
+
Bx0
Bx1
Bx2
Bx1 offsetindex
0
1
...
s0-1
BC2 BC1 BC0
By
y
BD0
BD1BD2
Λ0
addr
Bx ^0Bx0
C0C1C2index
0
1
...
M-1
ROM0
ROM1
...
Hình 4. Kiến trúc phần cứng mô hình phân đoạn tối ưu. 
Một ví dụ kiến trúc phần cứng của một mô hình phân đoạn tối ưu tính giá trị của một 
hàm số bằng phương pháp xấp xỉ đa thức theo (11) và được cho trong hình 4. Ở đây, 
chúng tôi lựa chọn đa thức bậc 2 với 3 tham số 0C , 1C và 2C để thực hiện việc xấp xỉ, 
nếu sử dụng đa thức bậc cao hơn thì kích thước bộ nhớ ROM1 lưu trữ các giá trị này sẽ 
phải tăng lên. 
 1 0...d dy C x C x x C (12) 
Với x là đầu vào, d và 0,...,dC lần lượt là bậc và các hệ số của đa thức xấp xỉ. Khối 
P2S tính toán phân đoạn tối ưu theo sai số định trước và khối Lựa chọn Bit thực hiện việc 
lựa chọn số lượng các bít của 0x , 1x và 2x thích hợp, đồng thời xác định địa chỉ để truy 
xuất các giá trị offset đã được tính toán và lưu trước vào trong các bộ nhớ ROM0 và 
ROM1. Để giảm kích thước của các bộ nhớ, phương pháp này sử dụng 2x để thay thế cho 
x trong công thức (11) và các giá trị offset được sử dụng để xác định các đoạn tương ứng 
được lưu trữ trong bộ nhớ ROM0 [12]. 
Hình 5-7 lần lượt minh họa các thiết kế phần cứng thực hiện kiến trúc trên. 
Hình 5. Module tính toán hàm icdf(‘Normal’, 0, 1). 
Hình 6. Module Address Decoding. 
Kỹ thuật điều khiển & Điện tử 
P. V. Hùng, , N. T. Lực, “Thiết kế phần cứng  chất lượng các bộ phát hiện ra đa.” 80 
Hình 7. Module tính giá trị 2f x . 
3.4. Tương quan nhiễu 
Ta có thể xây dựng các bộ lọc số FIR hoặc ứng dụng thuật toán FFT để thiết kế tương 
quan cho nhiễu Gauss đầu ra. Tuy nhiên như đã phân tích trong mục 2.3, để đảm bảo toàn 
vẹn tính thống kê và tương quan nhiễu ở đầu vào và đầu ra các bộ lọc, ta xác định mô 
phỏng nhiễu Gauss tương quan dạng mũ. Hình 8 là một thiết kế phần cứng đơn giản đáp 
ứng yêu cầu trên dựa theo công thức đệ quy (8). 
Hình 8. Thiết kế phần cứng tương quan nhiễu dạng mũ. 
4. KẾT QUẢ MÔ PHỎNG VÀ THẢO LUẬN 
4.1. Sơ đồ khối mô phỏng bộ tạo nhiễu 
Hình 9. Mô phỏng bộ tạo nhiễu. 
4.2. Một số kết quả 
Hình 10 là một so sánh giữa tín hiệu và phổ biên độ của đầu ra bộ tạo nhiễu không 
tương quan (hình bên trái) và tương quan với độ dài tương quan tương đối (hình bên phải). 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số 65, 02 - 2020 81
Cả tín hiệu đầu ra và phổ biên độ đều cho sự khác biệt về tương quan của nhiễu ở hai đầu 
ra bộ tạo nhiễu. 
Hình 10. Biên độ và mật độ phổ tín hiệu đầu ra bộ tạo nhiễu. 
Để kiểm tra thuộc tính thống kê biên độ các mẫu nhiễu ở hai đầu ra của bộ tạo nhiễu, ta 
sử dụng phép tích lũy mẫu theo biểu đồ Histogram để chia các mẫu nhiễu thành các 100 
cột và lưu giá trị tần suất vào trong đó. Hình 11 là một sự so sánh giữa hai đầu ra của bộ 
tạo nhiễu. Rõ ràng, tính thống kê ngẫu nhiên (hình bên trên) của các mẫu nhiễu ở đầu vào 
và đầu ra của module tương quan là không thay đổi. 
Hình 11. So sánh tính thống kê và tương quan nhiễu ở hai đầu ra. 
Sử dụng hàm autocorr.m trong Matlab để tính hàm tự tương quan của các mẫu nhiễu tại 
hai đầu ra của bộ tạo nhiễu. Hình 11 (hình bên dưới) là hàm tự tương quan của các mẫu 
nhiễu ở hai đầu ra. Hình bên trái cho thấy rằng, đầu ra thứ nhất của bộ tạo nhiễu là hoàn 
toàn không tương quan, trong khi hình bên phải cho thấy sự tương quan trong các mẫu 
nhiễu ở đầu ra cuối cùng của bộ tạo nhiễu. So sánh giữa lý thuyết (đường nét liền) và thực 
tế đầu ra của bộ tạo nhiễu (biểu đồ cột) cho chúng ta thấy một sự tương đồng về sự tương 
Kỹ thuật điều khiển & Điện tử 
P. V. Hùng, , N. T. Lực, “Thiết kế phần cứng  chất lượng các bộ phát hiện ra đa.” 82 
quan trong các mẫu nhiễu. 
Hình 12. Hàm mật độ phân bố nhiễu ở vùng biên độ lớn. 
Hình 12 thể hiện sự phân bố của các mẫu nhiễu tương quan ở đầu ra tương ứng với 
vùng nhiễu có biên độ lớn. Một sự phù hợp giữa nhiễu mô phỏng và lý thuyết thể hiện rõ 
trên hình. So sánh với kết quả mà [9] sử dụng các hàm sin, cos và log có sẵn trong thư 
viện phần cứng cho thiết kế Box-Muller dạng Fixed-Point và Float-Point, thì thiết kế này 
cho thấy sự phù hợp hơn rất nhiều. 
Hình 13. Mô phỏng nhiễu với các sự tương quan khác nhau. 
Hình 13 cho ta một mô phỏng khác khi thay đổi độ dài tương quan tương đối 12R 
và 6R . Chúng ta cũng thấy được rằng, khi R giảm ( R tăng) thì sự tương quan trong 
nhiễu đầu ra giảm, và ngược lại. Như đã phân tích ở trên, khi R tăng dần đến 30 (khi đó 
1R ) thì sẽ không còn sự tương quan trong nhiễu ở đầu ra. 
Một số kết quả thực tế sau khi nạp chương trình trên phần cứng Xillinx Virtex-4 
ML402 với sự hỗ trợ của công nghệ ChipScope Pro cho phép quan sát tín hiệu đầu ra dạng 
số ngay trên phần mềm của hãng. 
Hình 14. Nhiễu không tương quan thực tế. 
T
ần
 s
uấ
t 
m
ẫu
T
ần
 s
uấ
t 
m
ẫu
0 10 20 30 40
Số xung
-0.2
0
0.2
0.4
0.6
0.8
Nhiễu tương quan (R=12)
Thực tế
Lý thuyết
0 10 20 30 40
Số xung
-0.2
0
0.2
0.4
0.6
0.8
Nhiễu tương quan (R=6)
Thực tế
Lý thuyết
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số 65, 02 - 2020 83
Các kết quả trên hình 14 (đối với nhiễu không tương quan) và hình 15 (đối với nhiễu 
tương quan có R=20) cho thấy sự phù hợp về thuộc tính tương quan so với các kết quả mô 
phỏng trước đó. 
Hình 15. Nhiễu tương quan (R=20) thực tế. 
5. KẾT LUẬN 
Bài báo này đã đề xuất thiết kế một bộ tạo nhiễu Gauss trên cơ sở phần cứng FPGA, 
với đặc tính tương quan dạng mũ. Bộ tạo nhiễu này có khả năng ứng dụng trong hệ thống 
kiểm tra và đánh giá chất lượng của hệ thống ra đa nói chung và chất lượng các bộ phát 
hiện nói riêng. Ở đây, thiết kế này đã sử dụng bộ tạo nhiễu phân bố đều kiểu Tausworthe 
kết hợp có chất lượng tốt, sử dụng mô hình phân đoạn tối ưu để thực hiện chuyển hóa các 
mẫu nhiễu phân bố đều thành các các mẫu nhiễu phân bố Gauss độc lập thông quan hàm 
phân bố tích lũy nghịch đảo. Cuối cùng, các mẫu nhiễu được đưa qua bộ tương quan dạng 
mũ để có được đặc tính tương quan ở đầu ra. Các mô phỏng cho thấy sự phù hợp của kết 
quả đầu ra so với lý thuyết và có chất lượng tốt hơn so với một số bộ tạo nhiễu khác. Các 
kết quả thực tế cũng đã được đưa ra cho thấy sự phù hợp giữa nhiễu thực tế và mô phỏng. 
Thiết kế này là cơ sở cho sự phát triển các bộ tạo nhiễu không Gauss (phân bố Log-
Normal, Weibull, K) dựa trên FPGA để đánh giá toàn diện hơn chất lượng của các bộ phát 
hiện trong ra đa. 
TÀI LIỆU THAM KHẢO 
[1]. P. N. Anh, P. V. Hùng, N. M. Cường, "Xây dựng biểu thức toán mô tả phân bố nhiễu 
trong các vùng biển Việt Nam", Tạp chí Nghiên cứu KH&CN quân sự, Số 52 
(12/2017), tr. 60-67. 
[2]. P. N. Anh, P. V. Hùng, N. M. Cường, "Tính toán chỉ tiêu chất lượng phát hiện của 
một số chủng loại ra đa theo các điều kiện biển Việt Nam", Tạp chí Khoa học và Kỹ 
thuật, Số 187 (2017), tr. 140-153. 
[3]. A. Balleri, A. Nehorai, J. Wang, "Maximum likelihood estimation for compound-
gaussian clutter with inverse gamma texture", IEEE Transactions on Aerospace and 
Electronic Systems, Vol 43 (2007), pp. 775 - 779. 
[4]. D. Biebighauser, "Testing Random Number Generators", University of Minnesota 
(2000). 
[5]. A. ÇETİN, "CFAR Detection In K-Distributed Sea Clutter", A Thesis Of Middle East 
Technical University (2008). 
[6]. R. C. C. Cheung, D. U. Lee, W. Luk, J. D. Villasenor, "Hardware Generation of 
Arbitrary Random Number Distributions From Uniform Distributions Via the 
Inversion Method", IEEE Transactions on Very Large Scale Integration (VLSI) 
Systems, Vol. 15 (2007), pp. 952-962. 
[7]. E. Conte, A. D. Maio, C. Galdi, "Statistical Analysis of Real Clutter at Different 
Kỹ thuật điều khiển & Điện tử 
P. V. Hùng, , N. T. Lực, “Thiết kế phần cứng  chất lượng các bộ phát hiện ra đa.” 84 
Range Resolutions", IEEE Transactions on Aerospace and Electronic Systems, Vol 
40 (2004), pp. 903-918. 
[8]. Y. Dong, "Models of Land Clutter vs Grazing Angle, Spatial Distribution and 
Temporal Distribution – L-Band VV Polarisation Perspective", DSTO Systems 
Sciences Laboratory (2004). 
[9]. K. L. Fitch, K. A. Gillis, A. W. Harrison, "Digital Programmable Gaussian Noise 
Generator", WPI – MIT Lincoln Laboratory (2015). 
[10]. R. Gutierrez, V. Torres, a. J. Valls, "Hardware Architecture of a Gaussian Noise 
Generator Based on the Inversion Method", IEEE Transactions on Circuits and 
Systems, Vol. 59 (2012), pp. 501-505. 
[11]. P. L’ECUYER, "Maximally Equidistributed Combined Tausworthe Generators", 
Mathematics of Computation, Vol 65 (1996), pp. 203-213. 
[12]. D. U. Lee, R. C. C. Cheung, W. Luk, J. D. Villasenor, "Hierarchical Segmentation 
for Hardware Function Evaluation", IEEE Transactions on Very Large Scale 
Integration (VLSI) Systems, Vol. 17 (2009), pp. 103-116. 
[13]. D. U. Lee, J. D. Villasenor, W. Luk, P. H. W. Leong, "A Hardware Gaussian Noise 
Generator Using the Box-Muller Method and Its Error Analysis", IEEE Transactions 
on Computers, Vol. 55 (2006), pp. 659-671. 
[14]. B. R. Mahafza, "Radar Signal Analysis and Processing Using MATLAB", Chapman 
and Hall/CRC (2016). 
[15]. J. Muller, "Elementary Functions: Algorithms and Implementation", Berlin, 
Germany: Birkhauser Verlag AG (2005). 
[16]. E. Ollila, D. E. Tyler, V. Koivunen, H. V. Poor, "Compound-Gaussian Clutter 
Modeling With an Inverse Gaussian Texture Distribution", IEEE Signal Processing 
Letters, Vol 19 (2012), pp. 876-879. 
[17]. M. RANGASWAMY, D. WEINER, A. O. URK, "Computer Generation of 
Correlated Non-Gaussian Radar Clutter", IEEE Transactions on Aerospace and 
Electronic Systems, Vol. 31 (1993), pp. 106-116. 
[18]. S. Sayama, H. Sekine, "Weibull, log-Weibull and K-distributed ground clutter 
modeling analyzed by AIC", IEEE Transactions on Aerospace and Electronic 
Systems, Vol 37 (2001), pp. 1108-1113. 
[19]. M. J. Schulte, E. E. Swartzlander, "Hardware Designs for Exactly Rounded 
Elementary Functions", IEEE Transactions on Computers, Vol. 43 (1994), pp. 
946-973. 
[20]. M. I. Skolnik, "Introduciton To Radar Systems", McGraw-Hill (2001). 
[21]. S. Tezuka, "Random number generation based on polynomial arithmetic modulo 
two", IBM TRL Research Report (1989). 
[22]. K. Ward, R. Tough, S. Watts, "Sea Clutter: Scattering, the K Distribution and Radar 
Performance", The Institution of Engineering and Technology (2013). 
[23]. S. Watts, "Cell-averaging CFAR gain in spatially correlated K-distributed clutter", 
IEE Proceedings - Radar, Sonar and Navigation, Vol. 143 (10/1996), pp. 321-327. 
[24]. S. Watts, "A Practical Approach to the Prediction and Assessment of Radar 
Performance in Sea Clutter", IEEE Proceedings International Radar Conference, 
(1995), pp. 181-186. 
[25]. S. Watts, "Radar Sea Clutter: Recent Progress and Future Challenges", 2008 
International Conference on Radar, Vol. 1 (2008), pp. 10-16. 
[26]. S. Watts, K. Ward, G. Maria, "Radar Performance in Clutter - Modelling, Simulation 
and Target Detection Methods", The 13th European Radar Conference (2016). 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số 65, 02 - 2020 85
ABSTRACT 
THE HARDWARE-BASED DESIGN OF CORRELATED GAUSSIAN CLUTTER 
GENERATOR APPLYING IN THE TESTING AND ASSESSMENT SYSTEM 
OF RADAR DETECTORS’ PERFORMANCE 
 This article analyzes the model of correlated Gaussian clutter applied mainly in 
modelling of low-resolution radar systems with the effects of land and sea clutter 
(surface clutter). By analyzing the environmental conditions, we see that the impacts 
of correlation in the clutter on radar detectors’ performance are significant. Thus, 
the article proposes a design of correlated Gaussian clutter generator based on 
FPGA, which can apply in the testing and assessment systems of radar detectors’ 
performance, particularly low-resolution radar systems. The results in the output of 
the clutter generator compared with theory indicated the compatibility with both 
amplitude statistics and clutter correlation, and the performance of this generator is 
better compared with different based-hardware Gaussian clutter generators. 
Keywords: Radar; Detector; Radar Clutter; Correlation; FPGA. 
Nhận bài ngày 23 tháng 8 năm 2019 
Hoàn thiện ngày 25 tháng 11 năm 2019 
Chấp nhận đăng ngày 17 tháng 02 năm 2020 
Địa chỉ: 1 Học viện Kỹ thuật quân sự; 
 2 Học viện Bưu chính Viễn thông; 
 3 Học viện Phòng không Không quân. 
 * Email: hungpv_k31@lqdtu.edu.vn.